GM（1,1）模型在高铁软土路基沉降监测中的应用

林 飞，甄 龙，张 胜，陈俊平

（1.中国地质大学 信息工程学院，湖北 武汉 430070；2.杭州市勘测设计研究院，浙江 杭州310013；3.武警黄金四支队，辽宁 辽阳111000）

GM（1,1）模型在高铁软土路基沉降监测中的应用

林 飞1,2，甄 龙1，张 胜3，陈俊平1

（1.中国地质大学 信息工程学院，湖北 武汉 430070；2.杭州市勘测设计研究院，浙江 杭州310013；3.武警黄金四支队，辽宁 辽阳111000）

依托哈齐铁路客运专线沉降观测项目，利用灰色模型GM（1,1）对软土路基沉降进行定量分析预测，探讨了该沉降过程的动态变化规律。与实测数据对比表明，灰色模型GM（1,1）对该沉降趋势的符合度较高，精度能够满足要求。

灰色模型；GM（1,1）；沉降预测

与传统有砟轨道相比，高速铁路对线路的平顺性和稳定性要求更高，因此大多铺设无砟轨道。由于无砟轨道线路状态只能通过钢轨扣件内部较小的调节量（15 mm）调整[1]，所以高速铁路对线下工程的沉降变形要求非常严格[2]。在软土、松软土地基上修筑路基时，地基的沉降变形显得更为突出，沉降持续时间较长，将严重影响轨道的平顺性和稳定性，因此通过高速铁路沉降观测资料分析研究高速铁路软土路基沉降预测方法具有重要意义。软土路基的沉降一般为动态过程，测量时把软土路基看成静态系统，通过对多个不同离散时刻点的观测来分析其动态变化过程。实际上，软土路基的沉降本身具有“小样本”、“贫信息”和“不确定性”等特点[3]，一定程度上具有很强的灰色特征。所以本文依托哈齐铁路客运专线沉降观测项目，利用灰色模型GM（1,1）对软土路基沉降进行定量分析预测。

1 灰色模型GM（1,1）预测法及其精度评定

灰色系统是既包含已知信息又包含未知信息的系统[4]，它把表面上看似没有关系、随机性的数据进行处理，变成有规律的新序列。灰色系统预测的思路是：首先选择合适的方式把正的时间序列进行累加，使时间序列成为非负递增的数据列，然后选择合适的方法进行曲线拟合，把拟合得到的曲线作为预测模型[5]。

灰色模型GM（1,1）预测法的具体操作步骤如下：

GM（1,1）模型的白化微分方程为：

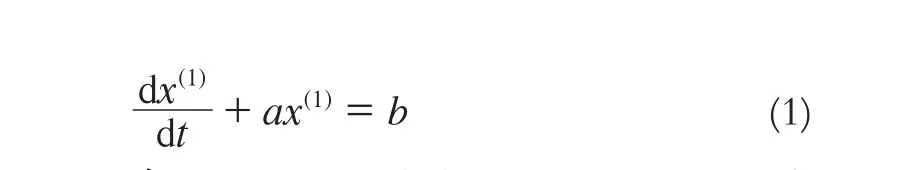
这是一个简单的一阶线性非齐次微分方程，对其进行求解，即

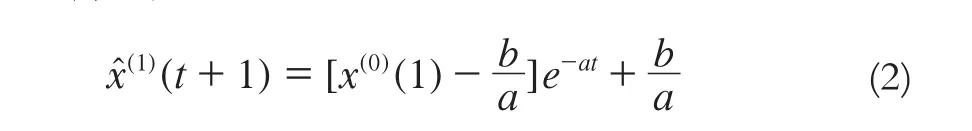
式中，a、b为灰色系统GM（1,1）模型的系数。

微分方程的系数可由最小二乘法解出，其向量形式为：

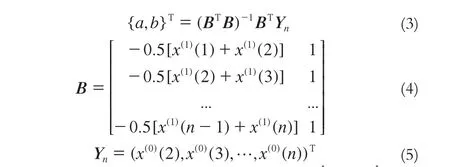
GM（1,1）模型的精度检验通常用后验差检验，具体步骤如下：

1）计算原始数据的还原值与其实际之间的残差：

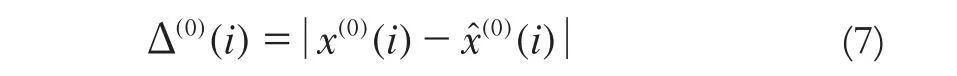
2）计算出原始序列的平均值：

3）计算原始序列X(0)的均方差：

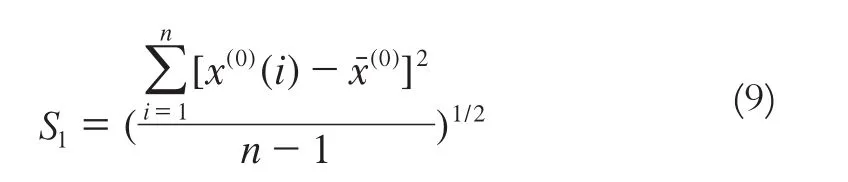
4）计算残差的均值：

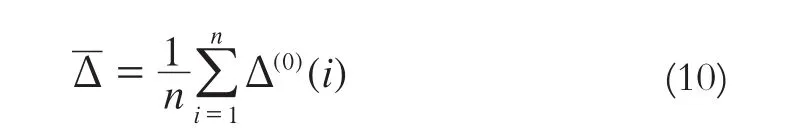
5） 计算残差的均方差：

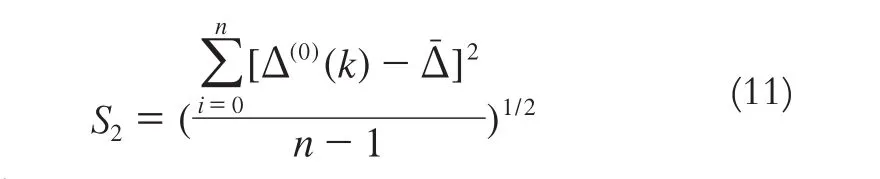
6） 计算方差比C：

7） 计算小残差概率：

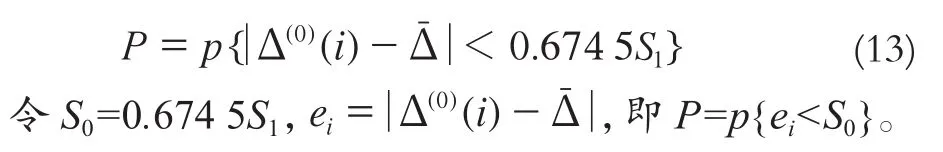
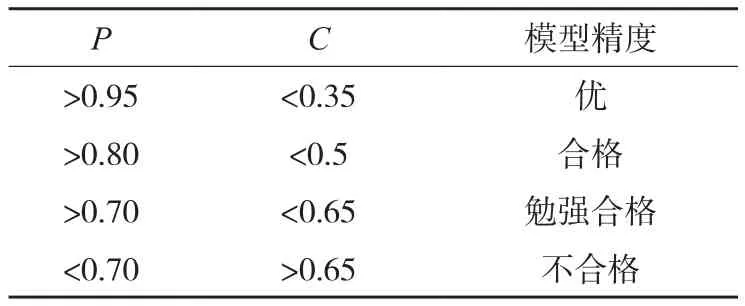
表1 后验差检验判别参照表

若相对残差、关联度、后验差检验在允许的范围内（表1），则可以用所建的模型进行预测，否则应进行残差修正。

2 预测实例

本文选取哈齐铁路客运专线一标段DK12+550断面的沉降板某段时期的6次观测数据作为预测起算数据，根据已有观测数据预测未来5次累计沉降数据，已知数据见表2。

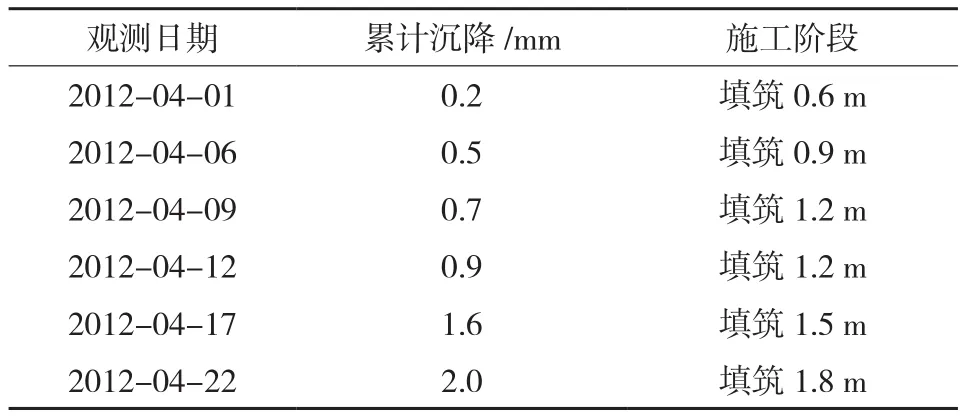
表2 DK12+550断面某段时期的沉降板沉降观测数据

2.1 计算过程

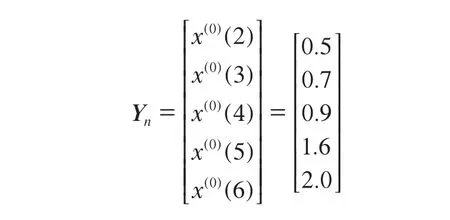
根据模型计算得出残差检验表如表3所示。进行后验差检验，将数据代入式（9）～（11），得S1=0.685 322 31，S2=0.092 249 12，则方差比C=S2/S1= 0.134 606 912 2＜0.35，小残差概率P=1＞0.95，对照表1可知检验结果为优。

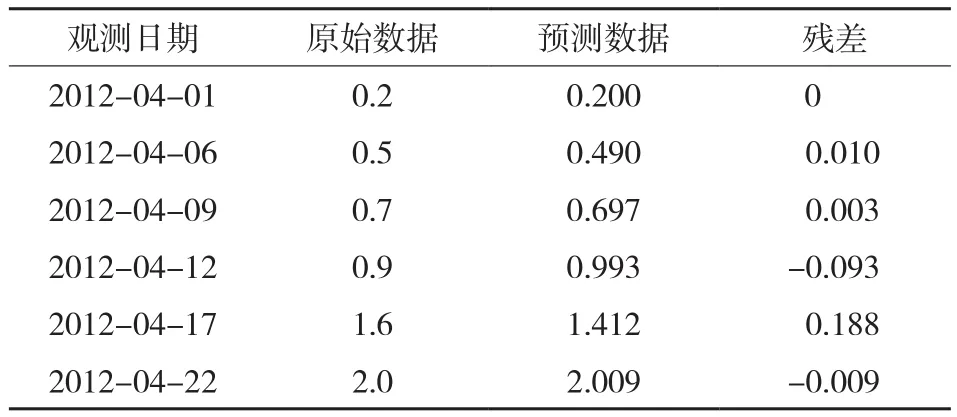
表3 GM（1,1）模型预测值和实际值比较

2.2 预测结果分析

根据已算出的预测模型可求得后面几次的沉降观测预测值，结果如表4所示。

表4 后5次的沉降观测预测值

由表3可知，实际的累计沉降量是逐渐增加的，预测的沉降量也是逐渐增加的，且残差基本比较小，且经过检验各项指标均为优等，达到一级精度标准，说明预测的总体趋势与实际情况是吻合的。从整体上来看，运用灰色模型GM（1,1）预测法对该软土路基沉降量的变化过程进行预测是可行的。

3 结 语

灰色模型相较于统计模型，在理论上更为严谨，且计算简便[6]。不过，在实际的运用中，因为高速铁路软土路基沉降是一个动态过程，受到系统内外多方面因素的综合作用，由灰色模型预测的远期数据所反映的沉降变化的真实程度会随着时间推移而逐步降低，这时应及时补充近期的观测数据，以提高预测精度[7]，从而更加真实地反映软土路基的沉降趋势。

[1] 张届,阮汝伟,李建平,等.水准尺倾斜对高铁桥墩沉降观测的影响研究[J].测绘通报, 2011(11):47-49

[2] 明祖涛,游振兴,张届,等.高速铁路桥隧沉降预测模型的研究[J].测绘通报,2011(8):17-19

[3] 刘思峰.灰色系统理论及其应用[M].北京：科学出版社,2010

[4] 李涛,张仪萍,张土乔.软土路基沉降的优性组合预测[J].岩石力学与工程学报,2005,24(18):82-86

[5] 邓聚龙.灰预测与灰决策[M].武汉:华中理工大学出版社,2002

[6] 鹿利军,杜子涛.灰色系统理论在建筑物变形分析中的应用[J].测绘与空间地理信息,2006,29(1):95-97

[7] 徐龙辉,贺跃光,曹诚.GM（1,1）模型在建筑物沉降监测中的应用[J].低温建筑技术,2010(9):94-96

P258

B

1672-4623（2016）03-0097-02

10.3969/j.issn.1672-4623.2016.03.031

林飞，硕士，研究方向为工程测量。

2014-02-25。