基于小波神经网络的桥梁变形监测预报

王万平，邹永玲

（1.陕西交通职业技术学院，陕西 西安 710018；2.长庆勘探开发研究院，陕西 西安 710021）

基于小波神经网络的桥梁变形监测预报

王万平1，邹永玲2

（1.陕西交通职业技术学院，陕西 西安 710018；2.长庆勘探开发研究院，陕西 西安 710021）

小波神经网络对建筑物变形预报具有较高的模型拟合及预报精度。从小波神经网络算法原理出发，阐述了使用该方法对所获得的桥梁变形监测数据进行模型建立及预报的过程，并利用Matlab实现了编程代码。通过对某桥梁变形监测预报的应用表明，该方法具有很强的可行性和实用性，可及早为桥梁变形预警，避免或减少灾害的发生。

小波神经网络；桥梁变形监测；变形预报；Matlab

随着我国现代建设的不断加快，超高墩、柱的桥梁急速增长,这些桥梁的形变关系到人民生命和财产安全，因此对这些桥梁进行变形监测就显得十分重要。经过数十年的发展，时间序列预测模型、小波分析方法和人工神经网络预测模型等方法的精度在不断提升，但还存在一定的局限性，如何取长补短，综合利用这些预测方法，将它们各自的优势进行整合，这一直是科学工作者研究的重点。小波神经网络将神经网络与小波变换进行整合，基于小波变换，借助非线性小波基，使其替代原本的非线性神经元激励函数，这样便构成了一种新型的神经网络模型。该模型继承了2种传统模型的优点，实现了优势整合；而在整合过程中不可避免地引入了2个新参变量：平移因子和伸缩因子，这样就能比小波分析分解更多的自由度。更多的自由度代表着更有效的函数逼近能力，只要对过程的各个参数选择合理，就可达到一个较好的预测结果，而这个过程需要的级数项组成，相比之前的分析方法，具有很大的便捷性。

本文利用小波神经网络模型，对桥梁的监测数据进行处理，主要借助于Matlab软件的编程实现。在完成建模的基础上，借助于现有的桥梁数据，对建立完成的模型进行了检验，用以判断其预测结果是否可靠。检验结果表明，所建模型是有效可行的，可实时对桥梁变形情况作预测，及早发现问题，从而避免或减少灾害的发生，为人民生命和财产提供保障。

1 小波神经网络预测模型

小波神经网络是借助于仿射小波的变换构造而成的一种神经网络。利用小波基函数取代传统的非线性神经元激励函数，是小波神经网络的特点。在该网络中，

可以利用小波基Ψab（x）拟合输入信号S^（t），其表示方法如下：

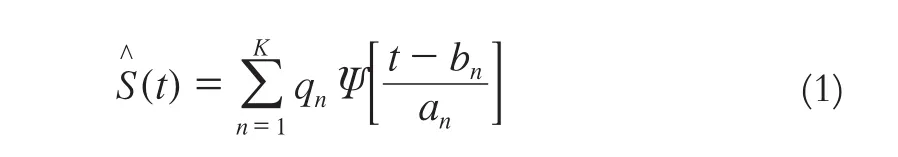
式中，an为伸缩因子；bn为小波基平移因子；qn为权值；S^（t）为拟合信号；K为小波基个数。

本文在参考多篇文献的基础上，最后选用Morlet母小波作为其小波基函数，其图形如图1所示，其表达式为：

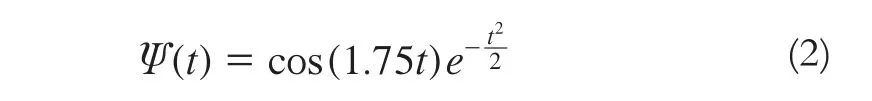
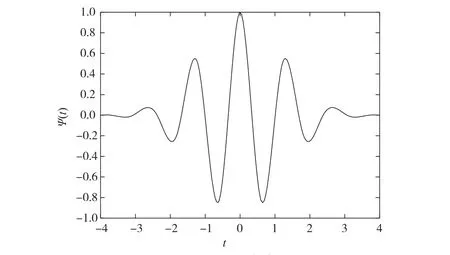
图1 Morlet母小波Ψ

设m代表网络输入的样本数量，c代表输出节点的个数，则第m个样本的c节点的输出数值为：

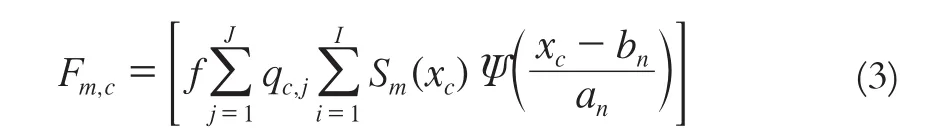
式中，I为输入层单元数；J为隐含层单元数；qc,j为第k位隐含层单元与第n位输出层单元之间的连接权值。

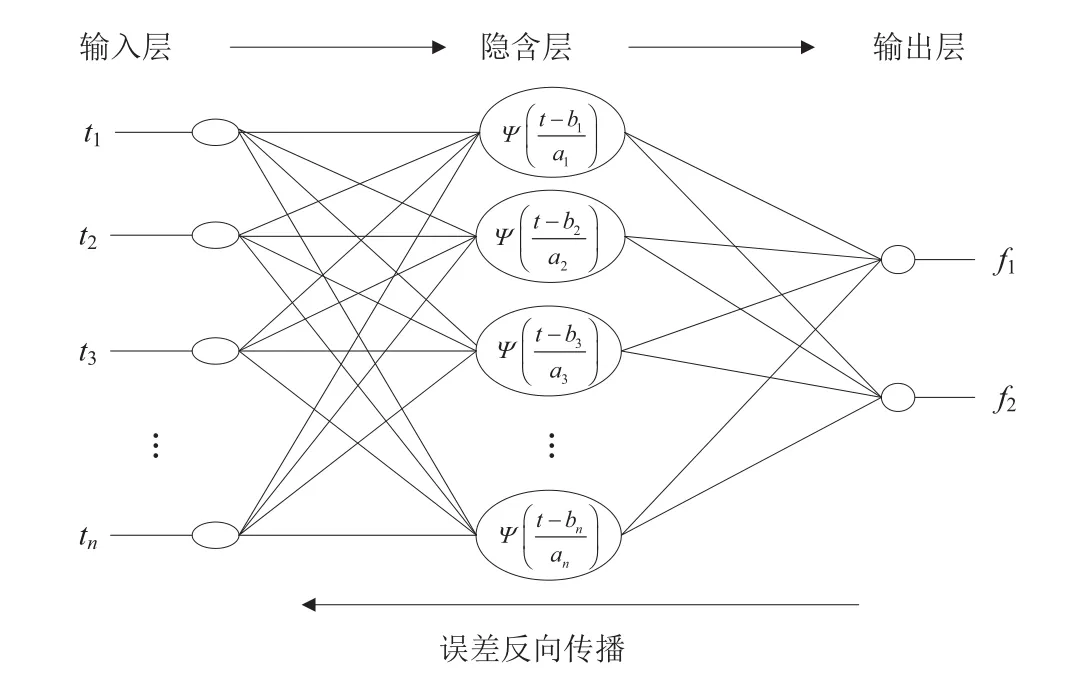
图2 小波神经网络结构

小波神经网络的算法主程序及其详细过程为：

1）对网络模型进行初始化参数定义。其主要包括对部分参数赋以随机初始值和对部分参数进行设置，第一部分的变量包括网络连接权重qn、小波伸缩因子an和平移因子bn；第二部分的参数包括容许误差e、网络学习率η和动量系数α。

2）为刚建立的基本网络提供学习样本。样本主要包括输入和输出两部分，其中输入向量有3个，分别为m（1，2，…，M）、Sm（xt）和t（1，2，…，I）；期望输出也有3个，分别为c（1，2，…，C）、Fm,c和m（1，2，…，M）。

3）建立网络的自学习方式，即实现计算网络实际输出Fm,c可由当前的网络参数算出的效果（见式（3））。

4）对计算网络的输出误差进行计算，其计算方法如下:

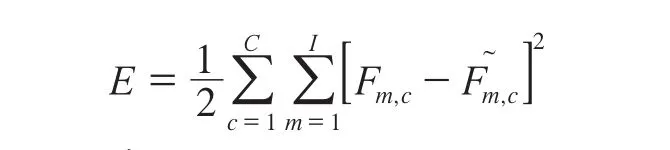
5）通过计算得到E值，当该值不大于规定的容许误差e时，则需要停止学习过程；同样，当迭代次数到达规定值时，也需要停止该过程；如果没有发生上述情况，则可进行下一步。

6）进行误差的反向传播，即沿误差函数变化的负梯度方向改变权值，然后利用梯度下降法对网络参数的变化值进行计算，且使误差反向传播；直至计算值符合要求，才终止程序。

小波神经网络模型作为一个整合，具有的优势为：

1）不存在结构上的盲目性。这主要与其整体和基元的结构理论有关，即小波理论。

2）具有更加快速的收敛速度。这主要是因为其基函数具有结构紧支性，因此神经元之间具有较小的相互作用，且该模型在进行学习时，只需调整很少的参数。

3）不存在局部最小点，即利用该模型可以找到一个全局的最优解。这主要是因为该模型的学习过程本质上是一个优化逼近过程，且其对象是一个凸向问题对象。

4）具有更加灵活高效的函数逼近能力。这主要是因为其引入了平移因子和伸缩因子2个新变量，其隐含层单元与小波基数也处于等量。

5）在输入信号不均匀时具有更好的准确性。输入信号不均匀，即数据点的分布不均匀，存在稠密区域和稀疏区域，针对这种情况，只有一个分辨率的传统激励函数不会分别对待，具有较大的误差。而小波神经元不同，其在数据稀疏区会用低分辨率学习，在稠密区就会用高分辨率。这种局部特性和不同的分辨率学习功能，可使模型与信号进行良好的匹配，从而提高预测的精度。

2 变形观测数据的处理与分析

本文选用Matlab软件进行语言编程，从而获得了小波神经网络模型的算法，并利用桥梁监测得到的实际数据对该算法模型进行验证，二者结果偏差符合要求。桥梁实例为：该数据来自某桥梁的5号沉降点在2012年10月～2013年5月期间的沉降变形观测值，每0.5个月进行一次监测，且记为1期，共有28期，结果如表1所示。首先选取1～20期的数据进行预报模型的建立；然后利用建立的模型进行沉降预测，模拟出21～28 期数据；最后将实测值和预报值进行对比，测量其误差，进行分析。

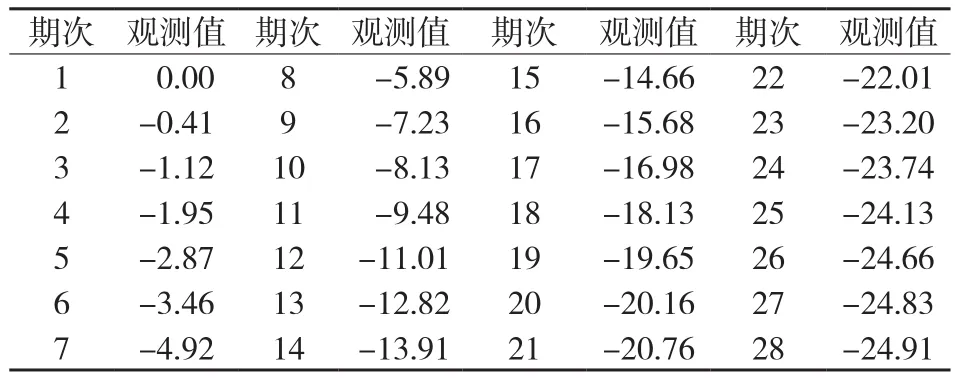
表1 某大桥5号桥墩沉降变形监测数据/mm

将实际监测过程中得到数据中的前20组作为输入参数，输入到在Matlab平台基础上建立的小波神经网络模型中，然后将模型计算得出的预报值和实测值进行对比，结果如表2、图3表示。

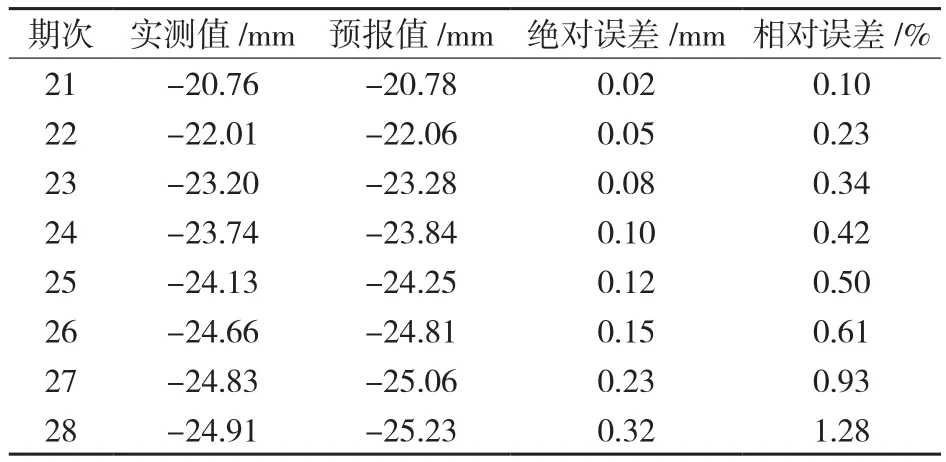
表2 实测值和预报值对照表

图3 实测值与预报值对照图

3 结 语

1）本文得到了利用小波神经网络模型对实际桥梁变形进行模拟的计算结果。该结果与实际值偏差符合要求，可对建筑物的沉降规律进行预测。

2）小波神经网络模型具有很高的学习精度和良好的泛化能力，同时能对 WNN 网络结构和网络参数进行优化。该算法既有较快的收敛性，又能及早地对建筑物变形做出预警，避免或减少灾害的发生。

[1] 潘国荣.地铁隧道变形的神经网络法预测[J].大地测量与地球动力学,2007,27(1):80-84

[2] 何勇.灰色马尔柯夫预测模型及其应用[J].系统工程理论与实践,1992,17(4):59-63

[3] 潘国荣,王穗辉.深基坑事故隐患的灰色预测[J].同济大学学报,1999,27(3):319-322

[4] 潘国荣,谷川.形变监测数据组合预测[J].大地测量与地球动力学,2006,26(4):27-29

[5] 潘国荣,谷川.变形监测数据的小波神经网络预测方法[J].大地测量与地球动力学,2007,27(4):47-50

[6] 邓勇,张冠宇,李宗春,等.遗传小波神经网络在变形预报中的应用[J].测绘科学,2012,37(5):183-186

[7] 刘娜,栾元重,黄晓阳,等.基于时间序列分析的桥梁变形监测预报研究[J].测绘科学,2011,36(6):45-47

[8] 牛东晓,邢棉.时间序列的小波神经网络预测模型的研究[J].系统工程理论与实践,1999(5):89-92

[9] 王建波,栾元重,许君一,等.小波分析桥梁变形监测数据处理[J].测绘科学,2012,37(3):79-81

[10] 黄敏,崔宝同,顾树生.基于小波神经网络的电梯交通流预测[J].控制与决策,2006(5):589-592

[11] 吕淑萍,赵咏梅.基于小波神经网络的时间序列预报方法及应用[J].哈尔滨工程大学学报,2004(2):180-182

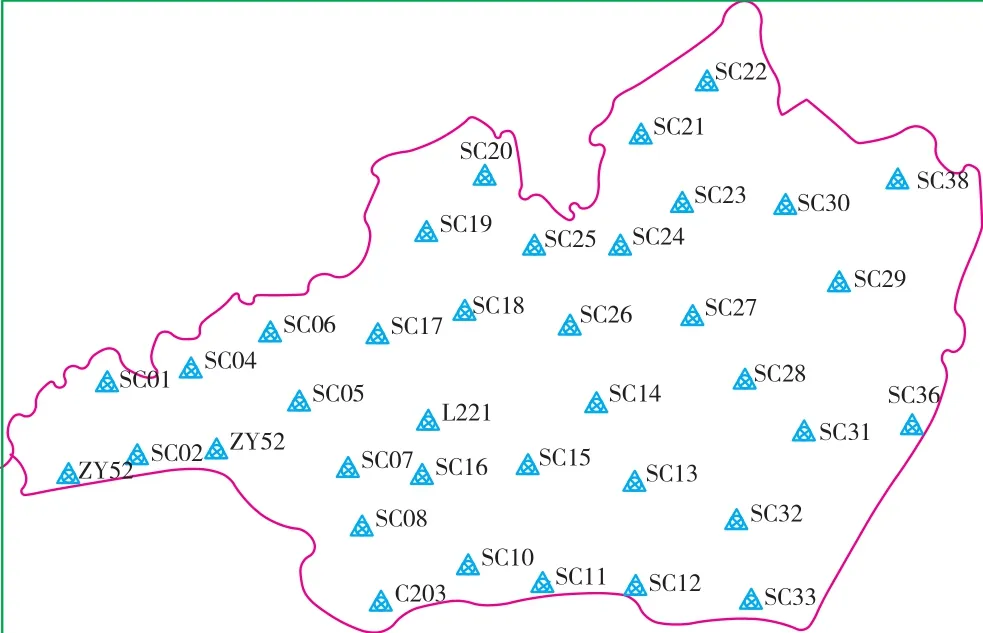
图2 项目GPS点和水准点点位分布图

4 结 语

本文主要研究了局部地区GPS拟合计算的各种方法，并根据具体工程实例，处理已有数据，经过比较得出一些有益的结论，归纳起来主要有：

1）用于GPS拟合的已知点需满足一定数量且均匀分布于测区，同时应将高程异常值的最大值和最小值的点也尽量选为拟合点，这样拟合的效果会更好。

2）二次多项式、三次多项式拟合方法，得到的结果能满足普通水准测量的精度的要求，但达不到四等水准的精度要求；而多面函数方法拟合GPS高程的精度可满足四等水准测量的精度要求。多面函数拟合法在山区获得四等水准测量的高程是可行的，最重要的因素在于结合不同的地形选择不同的拟合点和模型，同时最好设定一些点作为检核数据，从而验证GPS拟合的精度。

参考文献

[1] 于小平,杨国东,王凤艳,等.GPS高程拟合转换正常高的研究[J].测绘科学,2007,32(2):4-5

[2] 李征航,包满泰,叶乐安.利用GPS测量和水准测量精确确定局部地区的似大地水准面[J].测绘通报,1994(6):7-12

[3] 胡伍生,华锡生,张志伟.平坦地区转换GPS高程的混合转换方法[J].测绘学报,2002,31(2):128-133

[4] 李景卫,杨荫奎,高建,等.GPS高程拟合中多面函数及二次曲面函数的比较与分析[J].山东冶金,2006,28(3):42-43

[5] 徐绍铨,张华海,杨志强,等.GPS测量原理及应用[M].武汉：武汉大学出版社,2008

[6] 钟连棍,黄发秀.GPS水准拟合方式的统计分析及拟合方式的选择[J].工程勘察,2000(5):61-63

[7] GB/T12898-2009.国家三、四等水准测量规范[S].

第一作者简介：梁先兵，工程师，主要从事大地测量及工程测量相关方面的科研和生产工作。

P258

B

1672-4623（2016）03-0091-03

10.3969/j.issn.1672-4623.2016.03.029

王万平，讲师，主要从事工程测量方面的研究和教学工作。

2014-12-22。

项目来源：国家自然科学基金资助项目（4053021）；国土资源大调查资助项目（121201064140）;中国职业技术教育学会第四届理事会科研规划项目2014～2015年度立项课题资助项目（201428y04）；陕西省教育厅2015自然科学研究资助项目（15JK1066）。