聚焦数列热点题型

■浙江省杭州市萧山区第三高级中学

陈建华



聚焦数列热点题型

■浙江省杭州市萧山区第三高级中学

陈建华

数列是数学高考的重点内容，高考对数列的考查非常全面，既有对等差数列、等比数列的定义以及性质的考查，又有对数列与指数函数、对数函数和不等式的综合考查，还把极限思想和数学归纳法融入等差数列、等比数列中进行考查。新课标高考关于数列考点的命题，主要有以下几个方面：(1)对数列有关定义，等差数列、等比数列基本性质，基本运算的考查，常以选择题、填空题的形式出现，属容易题；(2)由简单递推式求数列的通项公式，进而求数列的前n项和，考查化归思想与几种常见数列求和类型的熟练程度，常以解答题形式出现，属中档题；(3)数列与其他知识的结合，有数列与函数、方程、不等式、解析几何的结合，以压轴题形式出现，其中以数列与函数、不等式的综合最为常见。

考点一 等差、等比数列的判定

考点二 等差、等比数列的基本运算与性质的运用

如图3、图4所示，在每个工作流程开始时，抓包机械手将梗包送到进包皮带上，在梗包被输送进负压箱体前进行人工拆麻绳，而后梗包被输送至勾包皮带上。当勾包光电开关检测梗包信号消失后，气缸驱动插包机构将梗包勾住并提起进行烟梗的倒出；然后夹包机构将麻袋内剩余的烟梗倒出并甩到出包皮带上送出，烟梗由出料皮带机送至定量皮带机+缓冲斗+电子皮带秤组合方式的恒流量控制系统。烟梗麻袋经人工解包后投料至定量皮带机，经定量皮带机储料仓、一级匀料辊匀料后为定量皮带机缓冲仓布料。

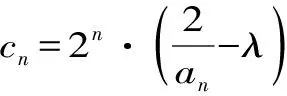
解析:①根据已知条件可求出等差数列的首项与公差，从而求得an和Sn。

解得a1=2，d=1。

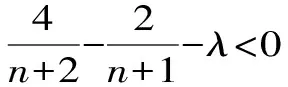
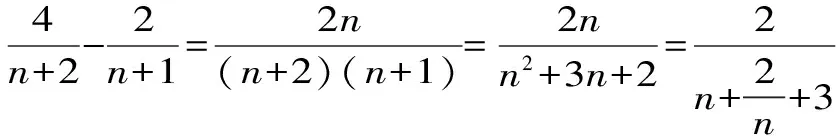
考点三 数列通项公式的求法

解析:根据已知条件求出公差，然后利用通项公式求出an，同时借助于数列的前n项和求出bn。

所以an=a5+(n-5)d=14+(n-5)×3=3n-1。由Sn=2n-1,得Sn-1=2n-1-1,n≥2,两式相减得bn=2n-1(n≥2)。又b1=S1=1，也满足上式，因此bn=2n-1。

考点四 数列的求和

(1)求an与bn；

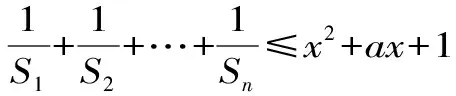
由题意知a3=3+2d=7。

S2b2=(6+d)·2q=32。

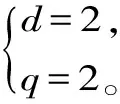
所以an=2n+1,bn=2n。

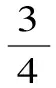
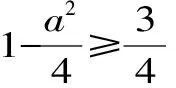
点评:在数列裂项求和时，只需考虑分母的结构，只要分母可以分成同一数列的相邻两项，就可以裂项，而分子只起到平衡等式的作用。

(责任编辑 徐利杰)