ABAQUS 软件在土石坝防渗设计中的运用
段佳捷(湖南省水利水电勘测设计研究总院 长沙市 410007)
ABAQUS 软件在土石坝防渗设计中的运用
段佳捷
(湖南省水利水电勘测设计研究总院 长沙市 410007)
在土石坝的防渗设计中,渗流场的水头、流速分布和渗流量都是影响防渗设计的主要因素。文章通过对ABAQUS软件的灵活运用,采用基于迭代原理求解稳定渗流自由面位置的方法指导防渗设计。计算结果表明,通过对ABAQUS软件的有效利用,可以大大提高效率,达到较好的效果。
ABAQUS软件 土石坝 防渗设计
引言
土石坝是历史最悠久的一种坝型,其造价低、结构简单、对自然条件适应性强、抗震性能好、工作可靠、寿命长等优点使其被广泛采用。土石坝作为挡水建筑物,它和渗流同时存在,土石坝的发展史也就是渗流理论和渗流控制理论的发展史[1]。在土石坝设计时,需要通过渗流计算来确定渗漏损失和合理的防渗排渗措施,同时坝型和坝的断面尺寸也经常需要借助渗流计算结果来比较确定。由于土石坝渗流场计算比较复杂,且存在渗流自由面随时间变化的问题。近年来,随着计算机软件和硬件的发展,能够考虑复杂边界、精确可靠、适用范围广的有限元法在土石坝渗流计算中的应用越来越受到工程设计人员的重视。
ABAQUS是由美国HKS公司开发的非线性有限元分析软件[2~3],在岩土工程方面,ABAQUS广泛的应用在边坡稳定分析、固结、渗流、蠕变、基坑开挖和地下开挖等复杂岩土力学问题的研究和计算中。
本文通过对ABAQUS有限元软件的变通运用,采用基于迭代原理求解稳定渗流自由面位置的方法对新疆塔日勒嘎水电站大坝进行渗流有限元分析,计算出坝体在稳定渗流期的各单元结点水头、下游逸出点和浸润线、并根据水力梯度矢量计算出渗透力,得到坝体在稳定渗流期的渗流场。此外,计算结果表明,该方法可更好地指导工程防渗设计,亦为类似工程的设计提供参考。
1 渗流有限元法计算原理
针对平面应变问题,在土骨架不可压缩的稳定渗流条件下,由水流的连续条件和达西定律可以得到土石坝的二维渗流方程[4][5]:
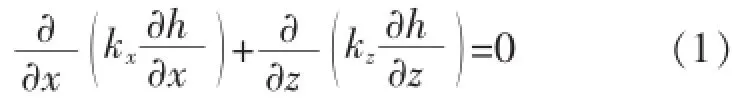
式中 kx、kz——分别为水平向与竖向的渗透系数(cm/s);
h——总水头(m)。
当kx=kz=k时,上式就化简为Laplace方程:

考虑介质和水体的压缩性时,同样可得非稳定渗流微分方程式:

式中 SS——单位储蓄水量,表示下降单位水头时,由于土骨架压缩和水的膨胀所释放出的储存水量(m3/m)。
流体的运动总是在限定的空间流场内发生的,要确定流场的分布仅靠渗流基本微分方程还是不够的,同时还需要借助边界条件和初始条件。渗流问题的定解条件中最重要的就是边界条件,一般存在三类边界条件[4]:
第一类边界条件为边界上给定位势函数或水头分布,或称水头边界条件。即:

第二类边界条件为边界上给出位势函数或水头的法向导数,或称流量边界条件,在这类边界条件上流量是已知的。即:

第三类边界条件为混合边界条件,是指含水层边界的内外水头差和交换的流量之间保持一定的线性关系,即:

式中 α、β为正常数,都是此类边界各点的已知数,无量纲。
对于无压渗流,内部无体积源时,整个渗流区域内水头函数为:

式中 φ——饱和流水头函数;
p——水压力;
R——水容重;
z——自某基准算起的高度。
采用有限元法求解无压渗流时,渗流自由面的确定一直都是一个难题。由于浸润线的位置事先是未知的,渗流自由面属于混合边界问题,必须同时满足水头边界条件和流量边界条件。如何合理确定渗流自由面,对于分析土石坝防渗设计具有重要的意义。
目前自由面的渗流计算,就其计算方法主要分为变动网格法和固定网格法两种[6]。变动网格法为首先假定一个浸润线,然后对浸润线以下区域划分网格,给定边界条件计算此假定渗流域,接着根据计算结果调整浸润线,重新划分网格,逐步迭代求解,直到浸润线上满足h=z的条件为止。固定网格法又分为剩余流量法、单元传导矩阵调整法、子单元法和初流量法等。而在目前的渗流分析中比较常用的是先对整个坝体划分网格,假定自由面以上区域内的渗透系数k远小于自由面以下区域内的渗透系数k,然后进行试算求解节点水头的单元传导矩阵调整法。变动网格法在进行目的为给出渗透力的渗流分析中,要不断地改变计算网格,工作复杂,计算量大。而在单元传导矩阵调整法中物理概念上有不妥之处:渗流不同于明渠流动,没有严格意义上的自由面;对浸润线同时给定水头边界和流量边界不符合力学原理(在弹塑性力学中也不能对一段边界同时给定位移和表面力)。
设计结合以上两种方法的优点,在土石坝的渗流有限元计算中,先划分网格,假设一个下游逸出点,计算出此时的零孔压线,然后再根据零孔压线与下游坝坡交点位置对逸出点进行修正。多次修正之后,直到修正的逸出点和计算出的逸出点位置相同,计算结束。此时,零孔压线就是浸润线。
2 算例分析
以新疆塔日勒嘎水电站大坝为例进行分析。塔日勒嘎水电站工程为克孜河中游河段规划的2库6级开发方案中的第二个梯级。
大坝为砂砾石坝壳粘土心墙坝,坝顶高程2254.00 m,坝顶宽8.0 m,坝顶长326.75 m,最大坝高45.00 m;上游坝坡坡比为1∶2.5,与上游围堰结合,在高程2 238.60 m处设有宽36.95 m的马道;下游坝坡坡比为1∶2.0。粘土心墙为对称心墙,位于坝壳料及反滤料上,其轴线位于坝轴线上游1.5 m处;心墙顶高程2 252.00 m,顶宽3.05 m,最大底宽24.60 m,最大高度36.00 m,心墙上、下游侧坡比1∶0.3;心墙两侧设反滤层及过渡层;心墙设置厚0.8 m的塑性混凝土防渗墙,入岩深度大于1.00 m,塑性防渗墙在心墙内部采用5.00 m×6.00 m(宽×高)的高塑性粘土进行包裹。水库正常蓄水位和设计水位都是2 250.00 m,设计下游水位为2220.152m。
该方案只选取河床部位最大横断面进行设计水位下的防渗设计、渗流复核计算,大坝典型断面、材料分区见图1所示。参照已往工程水工建筑物设计,取塑性混凝土防渗墙渗透系数为1.0×10-6cm/s,根据地质资料,河床浅部堆积的含漂石砂卵砾石层渗透系数为5×10-2cm/s,河床下部及右岸洪积的含土碎石渗透系数为(2.4×10-4~4.1×10-3)cm/s,古河床及阶地含泥、含漂砾砂卵砾石渗透系数为(2~5)×10-4cm/s,基岩上部弱风化区属中等至弱透水层(q=6.6~7 Lu),基岩下部微风化区属弱透水层(q≤5 Lu),坝体填筑材料渗透系数取值参见表1。
计算时考虑覆盖层及基岩的影响,将模型网格划分区域深至坝基以下55 m,上下游延伸至压重外30 m。渗流计算时基底为不透水边界,上游水位以下的上游坝坡和下游水位以下的下游坝坡为给定水头边界条件,逸出点(其最终位置靠迭代计算确定)到下游水位之间的下游坝坡为零孔压边界条件。
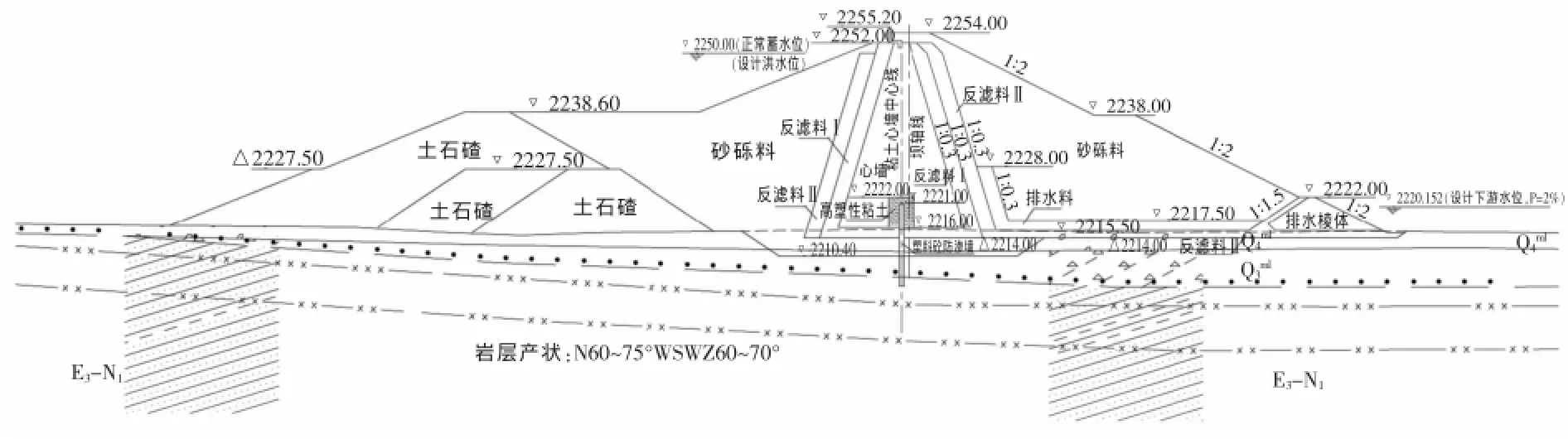
图1 塔日勒噶粘土心墙坝典型断面示意图(m)

表1 渗流计算材料参数表
该方法按防渗墙完全伸入下部不透水岩层和不伸入下部不透水岩层两种情况考虑。塔日勒嘎大坝典型断面逸出点计算的迭代过程如表2所示,迭代最终计算结果如图2~图5所示。图3、图5中零孔压线即为浸润线,零孔压线与下游坝坡的交点即为逸出点。

表2 浸润线计算过程

图2 用ABAQUS计算防渗墙未伸入基岩时流网图(单位:m)

图3 用ABAQUS计算防渗墙未伸入基岩时坝体孔隙水压力分布图(单位:m)

图4 用ABAQUS计算防渗墙伸入基岩时流网图 (单位:m)

图5 用ABAQUS计算防渗墙伸入基岩时坝体孔隙水压力分布图(单位:m)
在计算中,将整个坝体、坝基和排水棱体进行网格划分,但对排水棱体的透水性赋予一个相对较大的值。按照该方法,首先假定逸出点高程为下游水位与下游坝坡的交点,两种方案都仅仅通过两次试算既可求解到最终浸润线的逸出点,图3、图5坝体孔隙水压力的等值线分布图,根据其物理意义,孔隙压力为0的等值线即为浸润线。这些结果与文献[7]的结果是相吻合的;从计算结果中还直接地反映出,自由面以上的土体内具有负孔压,这些都与传统渗流理论的定性解释是一致的。
根据计算结果得出,塔日勒嘎土石坝在上述两种情况的单宽渗流量分别为15.65 m3/d和1.44 m3/d,根据二维有限元计算所得各点比降值图查得,防渗墙伸入基岩方案心墙内所有单元渗流梯度平均值为 2.20,下游出渗部位单元的最大渗透比降为3.42。混凝土防渗墙最大渗流比降为14.31,小于允许渗透比降80~100;坝基洪积堆积层最大渗透比降为0.05,小于允许渗透比降0.2~0.25。
计算结果表明,在心墙和防渗墙处零孔压下出现了骤降,防渗墙伸入基岩时防渗效果很明显,有效地降低了下游坝坡的孔隙水压力。计算结果还表明设置的坝内排水使坝体下游浸润线降低显著,效果较好。
3 结 论
通过上述计算分析结果表明:
(1)ABAQUS软件具有使用方便、功能齐全、运算速度快和计算精度高等优点。合理地运用ABAQUS软件到土石坝防渗设计中去,可以直观地看到计算过程,为实际工程问题的分析提供了新的研究思路,为类似工程的设计提供参考。
(2)塔日勒嘎土石坝采用粘土心墙加防渗墙防渗,防渗效果明显;尤其是防渗墙伸入基岩方案,大坝下游坝体基本上处于干燥区内,可以有效地降低浸润线。
(3)采用迭代法求解浸润线,此方法原理简单可靠,简化了计算工作量,可用于考虑复杂土工边值问题的渗流分析。
[1]刘杰.土石坝渗流控制理论的发展及实践[A].第四届全国水利水电工程渗流学术论文集[C].1993.
[2]庄茁,张帆,岑松,等.ABAQUS非线性有限元分析与实例[M].北京:科学出版社,2005.
[3]ABAQUS.2002 ABAQUS User's Conference Papers(US)[C].Hibbitte Karlsson&Sorenson INC,2002:115-126.
[4]刘杰,李广信.高等土力学[M].北京:清华大学出版社,2002. [5]钱家欢,殷宗泽.土工原理与计算[M].北京:水利电力出版社,1994.
[6]徐千军,张建红.确定稳定渗流自由面位置的一种简便方法[J].水动力学研究与进展,1999,14(4):418-423.
[7]张有天,陈平,王镭.有自由面渗流分析的初参数法[J].水利学报,1988(8):18-26.
2016-05-10)
段佳捷(1983-),男,湖南岳阳人,大学本科,工程师,目前从事水电工程设计工作。

