High temperature effects in moving shock reflection with protruding Mach stem
Xiaofeng Shi,Yujian Zhu,Xisheng Luo,Jiming YangAdvanced Propulsion Laboratory,Department of Modern Mechanics,University ofScience and Technology of China,Hefei230026,China
Letter
High temperature effects in moving shock reflection with protruding Mach stem
Xiaofeng Shi,Yujian Zhu∗,Xisheng Luo,Jiming Yang
Advanced Propulsion Laboratory,Department of Modern Mechanics,University ofScience and Technology of China,Hefei230026,China
H I G H L I G H T S
.Protrusion of Mach stem is induced by a wall-jetbehind it.
.High temperature effects intensify Mach stem protrusion.
.The mechanism is increase ofenergy buffer enhances wall-jet but weakens Mach stem.
A R T I C L E I N F O
Article history:
Received 31 May 2016
Received in revised form
12 July 2016
Accepted 7 August 2016
Available online 24 August 2016
Shock reflection Numericalsimulation Protruding Mach stem High temperature effects
The influence ofhigh temperature effects on the protrusion of Mach stem in strong shock reflection over a wedge was numerically investigated.A two-dimensionalinviscid solver applies finite volume method and unstructured quadrilateral grids were employed to simulate the flow.Theoretical analysis was also conducted to understand the phenomenon.Both numerical and theoretical results indicate a wall-jet penetrating forward is responsible for the occurrence of Mach stem protrusion.The protrusion degree seems to depend on the thermal energy buffer capacity of the testing gas.Approaches to increase the energy buffer capacity,such as vibrationalrelaxation,molecular dissociation,and increase of frozen heat capacity,all tend to escalate the protrusion effect.
©2016 The Author(s).Published by Elsevier Ltd on behalfof The Chinese Society of Theoreticaland Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).
Mach stemis normally treated as a straight shock perpendicular to the reflected wall in theoretical considerations of Mach reflection.It is however not always the case in reality.Protruding Mach stemhas been experimentally discovered by many[1-4].The protrusion not only makes the post-shock flow state deviate from the classical theoretical prediction,but also may fail the general transition criteria of reflection types.Recently,the phenomenon was also considered responsible for the shock bifurcation of cellular detonation wave[5,6].The protrusion ofMach stemmainly occurs under the condition of strong incident shock and low specific heat ratio ofgas[7].By numericalsimulation,Glaz et al.[8] discovered the wall jet-vortex rollup interaction structure which appears to integrate with the protruding Mach stem.Their results also implied thatthe thermochemicalnon-equilibriumeffecttends to intensify the interaction and therefore to escalate the protrusion. Li and Ben-Dor[9]analyzed the interaction between wall-jet and Mach stem and proposed an analytical model to calculate the flow field associated with corresponding wave patterns.Detailed characteristics of the wall-jetting process were later numerically investigated by Vasilev et al.[10].In the works of Li and Vasilev, nevertheless,the flow was considered thermo-chemically frozen and only mild Mach stem deformation was concerned.How the high temperature effect promotes Mach stem protrusion as well as the mechanism behind it has not yet been well understood. Therefore in this study,we carry out numerical tests on the Mach reflection of a strong moving shock over a wedge that has a protruding Mach stem,in which vibrational relaxation and chemical reactions are taking into account and their separate contributions are analyzed.
The numerical simulation is two-dimensional and inviscid. Dissociation chemistry and vibrational relaxation process of air molecules are built in with Gupta's 5-species chemical kinetic model[11]and Park's two-temperature model[12],respectively. The flow is simulated with finite volume method based on unstructured quadrilateral grids.Monotone upstream-centered schemes for conservation laws(MUSCL)-Hancock scheme[13] is employed to solve the parabolic part of the conservation equations,where the numericalfluxes are evaluated with a hybrid high level language(HLL)-high level language companion(HLLC) scheme[14].The pure thermochemical sources are integrated with a mature ordinary differential equation(ODE)solver-''VODE'',and join the parabolic part by fractionalsplitting method. Mesh adaptive technique is applied to accomplish a decent computational accuracy economically.
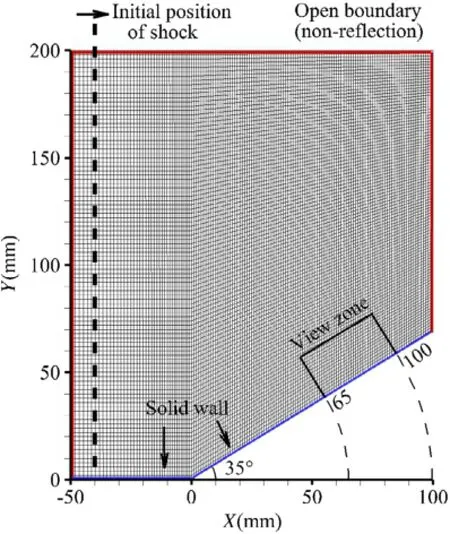
Fig.1.Background grids and boundary conditions of the computational zone.

Fig.2.Distribution of scaled density along the wedge surface.
The computational zone and the initial grids are shown in Fig.1.Floor and wedge surfaces are set as adiabatic slip walls, other boundaries are non-reflecting openings.The wedge angle is 35°.By 6 levels of adaptive mesh refinement,the grid size in regions of large density gradient may reach a minimum of 18µm, i.e.,1/7000 of wedge length.The initial temperature and pressure of the undisturbed flow are 293 K and 0.05 atm,respectively. Taking a test case from Ref.[8]for code validation,as plotted in Fig.2,it appears that the scaled density along the wedge surface between numericalresult and experimentaldata agrees well.
High temperature effects were known to have significant influences on the flow[8].To distinguish their particular influence, four gas models are tested,as listed in Table 1.
By varying the incident shock Mach number (Ms) and gas models, two types of typical flow patterns are observed. Representatives are shown in Figs. 3 and 4 (temperature contours). The view zone of the two figures is marked in Fig. 1. The basic wave systems of the two cases are both of double Mach reflection. Region (0) denotes the undisturbed flow. Region (1) denotes the flow behind the incident shock. Region (2) and region (3) are the flows behind the primary reflected shock (T-T′) and the primary Mach stem (T-G), which are separated by a slip line (T-D). And region (5) and region (4) are the flows behind the secondary reflected shock (T′-D) and Mach stem.

Table 1 Gas models.
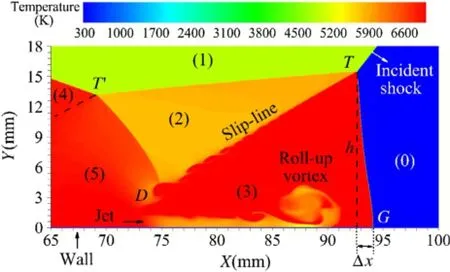
Fig.3.Temperature contours ofa DM-WR flow(Ms9,θw35°,frozen flow).

Fig.4.Temperature contours ofa TM-WR flow(Ms9,θw35°,thermochemicalnonequilibrium flow).
The two reflection types share a few common features.First,a jetis generated around the intersection ofslip line and wedge surface.The jet shoots forward along the surface and finally rolls up to form a vortex.Second,disturbed by the vortex,the lower part of the Mach stem protrudes as an arc,with the root of it keeping perpendicular to the reflecting wall.The difference mainly lies in the connection between the protruding part of the Mach stem and the rest.Figure 3 presents a whole piece of smoothly curved Mach stemwith no obvious conjunction,while in Fig.4 a new triple point is formed in the middle.Following the definition of Semenov[4], the former reflection is referred as double Mach-White reflection (DM-WR)and the latter as triple Mach-White reflection(TM-WR).
A non-dimensional parameter

is defined to characterize the protruding extent of the Mach stem, where h denotes the height of the Mach stem andΔx the distance between theoreticaland practicalpedals ofthe Mach stem.
The protrusion parameter f resulting from four different gas models are shown in Fig.5 for comparison.It is found that the boundary between DM-WR and TM-WR can be welldepicted by asingle f within the current testing range.That is,TM-WR generally happens when f exceeds 0.15,no matter what the gas modelis.

Fig.5.Non-dimensional deformation of Mach stem along with incident shock Mach number.
Gas models 1-3 consider only the difference of vibrational relaxation,but not dissociation.Clearly,thermal equilibrium flow always leads to a larger f than frozen flow.The protruding extent almost doubles.For thermal non-equilibrium flow,as expected, the deformation degree is between those of frozen and thermal equilibrium.When the incident shock Mach number is small, the Mach stem protrusion in thermal non-equilibrium flow is close to that in frozen flow.With the increase of shock Mach number,it approaches gradually towards the thermal equilibrium case.This is because the vibrational relaxation speed rises with the temperature,and the gas behind a weaker shock wave takes longer time to reach thermalequilibrium state,which is therefore more likely to remain partially frozen when passing through the reflection wave system.
Gas model 4 activates chemical reaction upon the basis of gas model 2.As well,the chemical reaction intensifies the protrusion of Mach stem.This effect becomes remarkable as the incident shock Mach number goes higher than 7,for this is where dissociation begins to massively occur behind the Mach stem and a considerable amount of atoms(first oxygen then nitrogen)will be produced afterward.The reason ofdissociation escalating Mach stem protrusion is to be explained later.At shock Mach number 8,the effect of dissociation seems to reach a maximum,after which the protrusion parameter f suddenly levels.Overall,the results indicate that the contribution of dissociation in Mach stem protrusion can be comparable to that of thermal relaxation.
Given the complexity of the jet and vortex flow behind the Mach stem,it is hard to predict the exact protruding extent. However,the qualitative effect ofprotrusion and the dependence of it may be estimated through certain calculations[9].The walljet is essentially driven by the pressure difference between regions (3)and(5)(Figs.3 and 4).Assuming isentropic jet,the velocity of the jet flow relative to point D,Vjet,can be easily deduced.On the other hand,the Mach stemkeeps drifting away frompoint D with a knowable velocity,VDG.The theoreticalprotrusion degree then can be expressed as the overriding degree of the jet,

withαa constant geometrical coefficient.The larger the value of fcis,the stronger the Mach stem protrusion is expected to be. Dismissingα,we introduce a theoreticalprotrusion factor


Fig.6.Jet intensity along with the shock Mach number in different gamma and equilibrium state conditions.
Figure 6 shows the d curves calculated with different gas models.Because the momentumdissipation ofjetand vortex is not considered in above derivation,the theoreticalresults significantly overestimate the protrusion extent.Despite that,the relativity and the variation trend of d turn out to be in good agreement with the numerical results of f in Fig.5.This confirms the mechanism of high temperature effects on the Mach stem protrusion lies in the fundamental fluid dynamics associated with the thermodynamic properties of gas.
The reason for the phenomenon is rather clear.The extra energy absorption of vibrational relaxation and molecular dissociation tend to weaken the strength of Mach stem.As a reversed process,the release of the extra vibrational energy and chemical energy stored in high temperature region(5)tends to induce a stronger jet in region(3).Under the same mechanism,simply increasing the heat capacity of gas should lead to a similar consequence.To demonstrate that,d for a higher frozen Cp(gamma=1.29)is calculated and plotted in Fig.6.It shows thathigher heat capacity indeed causes a larger protruding extent.
In summary,a numerical investigation of high temperature effects on Mach stem protruding phenomenon is carried out. Numerical results and theoretical analysis exhibit direct links between the wall-jet and the protrusion of Mach stem.High temperature effects including vibrationalrelaxation and molecular dissociation tend to escalate the protrusion.Increase of heat capacity favors protrusion as well.The mechanism behind them is essentially the same.There is a strength competition between two opposite processes-the Mach stem compression and the wall-jet expansion.The balance between them seems to greatly depend on the buffer capacity ofthermalenergy.The larger the buffer capacity is,the weaker the compression and the stronger the expansion will be,and therefore the more severely the Mach stem will be disturbed by the jet.
[1]S.Ando,Pseudo-stationary oblique shock-wave reflection in carbon dioxide -domains and boundaries,Technical Report,UTIAS Technical Note No.231, 1981.
[2]J.Lee,I.Glass,Domains and boundaries of pseudo-stationary oblique shock-wave reflection in air,TechnicalReport,UTIAS Technical Note No.262, 1982.
[3]J.Foster,P.Rosen,B.Wilde,et al.,Mach reflection in warm dense plasma,Phys. Plasmas 17(2010)112704.
[4]A.Semenov,M.Berezkina,I.Krassovskaya,Classification of pseudo-steady shock wave reflection types,Shock Waves 22(2012)307-316.
[5]P.Mach,M.Radulescu,Mach reflection bifurcations as a mechanism of cell multiplication in gaseous detonations,Proc.Combust.Inst.33(2011) 2279-2285.
[6]L.Maley,R.Bhattacharjee,S.Lau-Chapdelaine,et al.,Influence of hydrodynamic instabilities on the propagation mechanism offast flames,Proc.Combust.Inst.35(2015)2117-2126.
[7]I.Glass,Some aspects ofshock-wave research,AIAA J.25(1987)214-229.
[8]H.Glaz,P.Colella,J.Collns,etal.,Nonequilibriumeffectsin oblique shock-wave reflection,AIAA J.26(1988)698-705.
[9]H.Li,G.Ben-Dor,Analysisofdouble-mach-reflection wave configurations with convexly curved mach stems,Shock Waves 9(1999)319-326.
[10]E.Vasilev,G.Ben-Dor,T.Elperin,et al.,The wall-jetting effect in mach reflection:Navier-Stokes simulations,J.Fluid Mech.511(2004) 363-379.
[11]R.Gupta,J.Yos,R.Thomopson,et al.,A review of reaction rates and thermodynamic and transport properties for an 11-species air model for chemical and thermal nonequilibrium calculations to 30000 k,Technical Report,AIAA,1985.
[12]C.Park,On convergence of computation of chemically reacting flows, Technical Report,AIAA,1985.
[13]E.F.Toro,Riemann Solvers and NumericalMethods for Fluid Dynamics,Spring Press,1997.
[14]H.Nishikawa,K.Kitamura,Very simple,carbuncle-free,boundary-layerresolving,rotated-hybrid riemann solvers,J.Comput.Phys.227(2008) 2560-2581.
∗Corresponding author.
E-mail address:yujianrd@ustc.edu.cn(Y.Zhu).
http://dx.doi.org/10.1016/j.taml.2016.08.006
2095-0349/©2016 The Author(s).Published by Elsevier Ltd on behalfof The Chinese Society of Theoreticaland Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
 Theoretical & Applied Mechanics Letters2016年5期
Theoretical & Applied Mechanics Letters2016年5期
- Theoretical & Applied Mechanics Letters的其它文章
- Two-dimensionalmodeling of the self-limiting oxidation in silicon and tungsten nanowires
- Subset-based localvs.finite element-based globaldigitalimage correlation:A comparison study
- Magnetic induction strength on surface of a ferro-medium circular cylinder
- Numericalinvestigation of unsteady mixing mechanism in plate film cooling
- The Richtmyer-Meshkov instability of a'V'shaped air/helium interface subjected to a weak shock
- Side force controlon slender body by self-excited oscillation flag
