基于深度图像的室内三维平面分割方法研究

陈正兵

（南京理工大学 计算机科学与工程学院，江苏 南京210094）

基于深度图像的室内三维平面分割方法研究

陈正兵

（南京理工大学 计算机科学与工程学院，江苏 南京210094）

当前随着3D相机在智能机器人领域的广泛运用，越来越多的学者投入到了基于3D相机深度图像的室内三维平面分割研究当中。文运用了一种快速而且比较稳定的方法去检测复杂的平面，其中深度图像是运用Kinect相机采集的。为了提高平面提取的速度，我们首先计算深度图像中点的法向量，通过法向量来判断这些点是否在一个平面上。运用求点的法向量可以同时检测多个复杂的平面，而且实验结果显示该方法比传统的3D Hough Transform以及RANSAC方法要快。此种方法还有个优点就是可以运用到实时的平面与障碍物检测当中，此方法在机器人领域有比较大的应用前景。

平面提取；深度图像；法向量；Kinect相机

目前基于深度图像的三维场景分割的主要优点是可以帮助机器人认识和理解周围的环境，而且机器人周围的环境以及障碍物都是平坦的，或者说可以分解为平面区域。所以基于深度图像的室内三维场景分割也可以转化为对室内三维场景的平面分割，当前平面分割算法主要是基于两个标准，一个是基于框架，你一个是基于特征。基于框架的平面提取算法主要有：区域生长算法[1]，聚类算法[2]和边缘检测算法[3]。基于特征的平面分割算法主要有：法向量算法[4]和扫描线分割算法[5]。深度图像提取和分割是物体识别定位和特征提取之前的重要步骤，受到了较多研究人员的关注。由于深度图像的分割是图像各种处理和分析的基础，而分割结果的好坏直接影响着后续的数据处理效果，并且对数据分割这方面的研究还没有一个符合一般情况的成系统性的成果，所以到现在，深度图像的分割问题还一直是研究的热点和难点之一。当前平面提取方法种类比较多，国内外许多学者对这个方面提发表了自己的研究成果，国外学者提出的基于深度图像的梯度进行平面分割[6]，充分运用到图像的梯度信息从而完成深度图像的平面提取，李宝等人[7]提出的一种基于RANSAC的点云特征线提取算法，对点云的噪声、外点和数据缺失有很强的鲁棒性。国内钱伟宁[8]等人基于大量的距离和深度信息对平面提取进行了研究。

在传统的平面检测方法中，需要解决的也是面临的主要难点是怎样改进数据处理的速度。在3D Hough Transform[9]方法需要使用所有的点，在计算的过程中计算的复杂度比较高，效率比较低。RANSAC[10]方法是一种很早之前就提出来的一种方法，但是该方法存在重复计算，复杂度较高，效率相对3D Hough Transform方法更低。基于RANSAC平面提取的方法存在执行时间的缺点，假设所利用的是可靠的点（认为存在的噪声点较少）而不是随机的点，将会减少迭代的过程，从而提高该方法的效率。该算法首先是对点云进行抽样，得到一定数量点云集，然后通过奇异值分解的方法得到类别相似的点然后进行归类，然后对归类好的点进行平面拟合，反复进行抽样直到所有的点都被分类，然后进行平面拟合，最后得到点云数据的平面图。

1 利用求法向量的方法进行平面分割

在本篇文章中我们所采用的是法向量算法，深度图像是通过采集室内封闭的环境，并且该环境内有光照，在满足该条件的情况下，我们利用Kinect相机能够采集到在该环境下的深度图像，同时也可以得到相对应的彩色图像。通过以上条件我们可以很轻松的通过Kinect相机得到3D点云数据。传统的处理3D点云数据是计算每个3D点之间的距离，在本篇文章中我们所采取的方法是计算3D点云的法向量[11]，通过法向量来判断3D点是不是在一个平面。

如上图所示，文中提到的算法主要是先求出所有点云的法向量，然后根据法向量的方向判断点云的类别，然后同样利用奇异值分解的方法对所有点云进行分类，对于分类好的点云进行平面拟合。

1.1 点云法向量计算的研究现状

当前法向量的计算方法大致可以分为3类：基于点云数据局部表面拟合的方法，基于Delaunay方法，基于鲁棒统计的方法。

1）基于点云数据局部表面拟合的方法是由 Hugues Hoppe[12]等人基于有向距离函数（Signed Distance Function）的三维点云表面重建算法中提出。这种方法的原理主要是将K个最近点拟合出的平面的法向量作为当前点的法向量。

2）基于Delaunay[13]方法。该方法的原理主要是首先为点云构建Voronoi图，然后进行Delauney三角划分，对于点云数据中的每个点，假设点处于整个点云的凸起的部位内，我们可以将所在的Voronoi栅格中距离最远的顶点的连线作为点的法向量。OuYang等人[14]在这种方法的基础上做了一些该进，他们为点的领域构建一个局部的Voronoi图，然后为该Voronoi图拟合一组二次曲面，通过计算这些二次曲面的切向量来计算点的法向量。Alliez等人[15]提出将PCA方法和Voronoi方法相结合，这种方法可以得到比较可靠的法向量，但是点云中存在的一些尖锐特征仍然没有考虑进去。

3）基于鲁棒统计的方法。

基于鲁棒统计的方法Fleishman等人提出了利用鲁棒的移动最小二乘（Robust Moving Least Squares，RMLS）来重建点云数据中具有尖锐特征的表面，对于给定的点云中的一个点，我们将它分为多个没有外点的光滑区域，对于这些子区域我们进行投影，在进行表面重建的过程中，我们可以通过重建的分片光滑表面得到。

1.2 计算点云的法向量

文中利用了sobel算子来计算点云的法向量，sobel算子在图像中是用来进行边缘检测的，它是基于一阶导数的边缘检测算子，但是在进行边缘检测的同时我们可以得到图像边缘方向和幅度两个属性，基于这个启发，在三维点云数据的法向量计算过程中，我们可以使用sobel算子的这些特性来计算点云数据中某一点的空间法向量。在二维图像中sobel算子包含两组3×3的矩阵:文中利用sobel算子计算空间点的法向量时取的两个常量sobel_u，sobel_v，由于空间某一点对应的邻近点有8个，在计算法向量时我们两个常量的取值分别为：

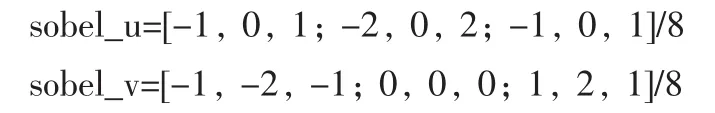
在二维图像中我们通过卷积可以得到图像边缘点的幅度和方向的变化[16]，利用此原理，在三维空间中通过卷积可以得到空间中三维点的法向量。首先我们利用 sobel_u对空间八个点进行卷积得到矩阵B1，利用sobel_v对空间八个点进行卷积得到矩阵B2，然后计算矩阵B1的各项和b1，计算矩阵B2的各项和b2，利用b1和b2得到新的矩阵B=[b1；b2；1]，再由矩阵A=[1，0，0；0，1，0；x，y，1]以及单位矩阵I进行卷积得到法向量N=I.*A.*B，由此方法可以快速得道点云的法向量。在计算法向量时由于一些边界点没有邻近的空间8个点，因此我们在计算的时候边界点先不取值，点云边界点的法向量设为其邻近点一致。

1.3 对3D点云数据进行分类

为了提高点云数据处理的速度，我们采取的是均匀采样的方法而不是单独的对每个点进行处理，当进行均匀采样的过程中，能够确定哪些点在一个平面上，哪些点不在一个平面上，判断两个点是否在同一个平面上的方法主要通过以下方法确定：

Ni和Nj分别是点Pi和Pj对应的法向量，方程（1）用来确定法向量相同的点，方程（2）是用来两个法向量两相同的点的连线是否与两个点的方向量垂直，通过这种方法可以对3D点云进行分类，从而判断哪些点是在同一个平面上。

1.4 平面提取

经过之前对3D点云数据分类之后，对于点云数据对应的平面方程就可以确定，该平面可以用方程式（3）表示，为了从多个复杂的点中提取平面，矩阵方程（4）是约束条件。

在上面的方程中，Xi是一个被分离的点集，n是这个点集中点的数目，结合以上的方程再利用SVD（奇异值分解）方法来处理数据。

1.5 通过比较平面方程的系数来处理相同的平面

最后对于那些系数比较相近的平面我们可以将他们去除掉，那些包含最多点的平面被保留下来而其余的则被去除，假设两个平面一样则有：

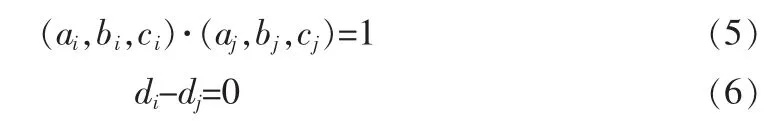
在这个方程中，a，b，c，d是平面i和j的平面方程系数。方程（5）检测的是两个平面的角度是一样的。假如方程（5）满足，方程（6）检测的是两个平面的距离为0。在这部分中，我们设定一个阈值，假如平面的参数在这个阈值内则我们可以判定这些平面是一个平面，假如方程式（5）和（6）在这些阈值范围内是成立的则可以判断这些平面是相同的平面。

2 实验结果

以下两幅图像是用kinect相机采集的彩色图和深度图，根据kinect相机的原理，在采集到的信息中包含图像的点云信息。

图2 深度相机采集的彩色图和深度图

先对深度图像的点云数据求其法向量，得到点云法向量的坐标，然后对法向量进行分类，得到的图如图3所示。

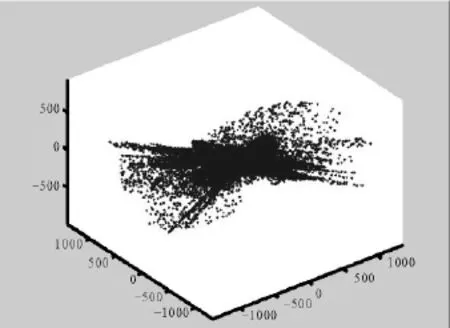
图3 点云法向量

在求出三维点云的法向量后[17]，我们根据之前提出的方法进行平面提取得到三维图像如图4所示。

图4 提取的平面分割图

在进行本方法的同时我们也利用传统的 3D Hough Transform方法和RANSAC方法进行了比较，得出的结论如表1所示。

表1 3种平面提取方法比较

为了和之前提出的方法进行比较，我们利用之前提到的两种方法进行了实验，运行的环境都是在matlab 2012b，从上表可以看出，本文提出的方法在处理上大大缩短了运行的时间，这在平面提取涉及到的应用上有了比较大的优势，当然本方法也是在结合传统平面提取方法上的一种改进。

我们提出的方法是在酷睿 i5-3230M双核处理器（2.6 GHz，睿频可达3.2 GHz）为主板的计算机上进行运算的。

3 结 论

在文中我们提出了一种基于Kinect深度相机的室内三维平面分割方法，我们所用的是通过计算点云数据的法向量，然后对法向量进行分类，最后通过分类后的法向量来提取平面。从结果我们可以看出，我们采用的方法所用的时间较其他两种方法有明显的优势。相比较而言，3D Hough Transform所用的时间是文中提出的方法的好多倍，而且需要较大的存储空间来保证结果的准确性。而且文中提出的方法不需要迭代，因此这种方法比RANSAC方法更快，虽然准确性上几乎一样。

[1]秦晓薇.区域填充算法的研究[J].赤峰学院学报：自然科学版，2011，27（6）：47-49.

[2]Johnson A E，Hebert M.Using spin-images for efficient multiple model recognition in cluttered 3-D scenes[J].PAMI，1999，5（21）:433-449.

[3]Goerzen C，Kong Z，Mettler B.A survey of motion planning algorithms from the perspective of autonomous uav guidance[J].JournalofIntelligent& Robotic Systems，2010，1（57）：65-100.

[4]WoodenD，Egerstedt M.Oriented visibility graphs:Lowcomplexity planning in real-time environments[J].IEEE，2006，2（31）:2354-2359.

[5]Kuwata Y，How J.Three dimensional receding horizon control for uavs，AIAA Guidance[R].Navigation，and Control Conference and Exhibit，2004，3（1）:2100-2113.

[6]Enjarini B，Grser A.Planar segmentation from depth images using gradient of depth feature[J].2012 IEEE/RSJ、International Conference on Intelligent Robots and Systems October 7-12，2012，2（1）:4668-4674.

[7]李宝，程志全，党岗，等.一种基于RANSAC的点云特征线提取算法[J].计算机工程与科学，2013，35（2）:147-152.

[8]QIAN Wei-ning，GONG Xue-qing，AO Ying-zhou.Clustering in very large databases based on distance and density[J]. Journal of Computer Science andTechnology，2003，18（1）: 67-76.

[9]DoritBorrmann.The 3D Hough Transform for Plane Detection in Point Clouds:A Review and a newAccumulator Design[N].3D Research Center and Springe，2011（2）：2092-6731.

[10]Fischler M A，Bolles R C.Random samples conse-nsus:A paradigm for model fitting with application to image analysis and automated cartography [J].Communicatio-ns of the ACM，Null，1981，6（24）：381-395.

[11]Dirk Holz，Stefan Holzen，Radu Bogdan Rusu，and Sven Behnke，Real-Time Plane Segmentation Using RGB-D Cameras [J].RoboCup 2011，LNCS7416，2011，5（11）:306-317.

[12]Hugues Hoppe，Tony DeRose，Tom Duchamp，et al.Surface Reconstruction from Unorga-nized Points[C]//University of Washington Seattle，1992：71-78.

[13]Nina Amenta，Marshall Bern.Surface Reconstruction by Voronoi Filtering[J].Discrete and Computational Geometry，1998（22）：481-504.

[14]Daoshan OuYang，Hsi-Yung Feng，“On the normal vector estimation for point cloud data from smooth surfaces”[J]. Computer-Aided Design 37，2005，3（2）：1071-1079.

[15]Alliez P，Cohen-Steiner D，Tong Y，et al.Voronoi-based VariationalReconstruction ofUnoriented PointSets[J]. Eurographics Symposium on Geometry Processing，2007，2（5）：1009-1018.

[16]南向军.宽马赫数二维曲面压缩高超声速进气道设计[J].火箭推进，2015(1)：43.

[17]余武江，王海洲，陈二锋，等.单向阀三维动态流场稳定性仿真研究[J].火箭推进，2015(1)：82.

Indoor three-dimensional plane segmentation method based on depth image research

CHEN Zheng-bing
（College of Computer Science and Engineering，Nanjing University of Science and Technology，Nanjing 210094，China）

With the wide application of 3D camera in the field of intelligent robots，more and more scholars have devoted to the study of 3D plane segmentation based on the depth image of 3D camera.In this paper，a fast and relatively stable method is used to detect the complex plane，and the depth image is acquired by Kinect camera.In order to improve the speed of plane extraction，we first calculate the normal vector of the depth of the image，and judge whether these points are in a plane by the normal vector.The normal vector of the point can be detected simultaneously by a number of complex planes，and the experimental results show that the proposed method is faster than the traditional Hough Transform 3D and RANSAC method. This method has the advantage that it can be applied to real-time detection of planar and obstacles，and this method has a relatively large application prospect in the field of robotics.

plan extraction；depth image；normal vector；Kinect camera

TN919.8

A

1674－6236（2016）24-0158-03

2015-12-09 稿件编号：201512109

陈正兵（1986—），男，湖北鄂州人，硕士。研究方向：三维点云特征提取。