基于参量阵的水声通信信道分析

李 伦，陈 敏，袁寿星，胡伦川

（电子科技大学 航空航天学院，四川 成都611731）

基于参量阵的水声通信信道分析

李 伦，陈 敏，袁寿星，胡伦川

（电子科技大学 航空航天学院，四川 成都611731）

为了减少水声通信信号在传播过程中的多途干扰，提高水声通信系统的抗干扰能力，提高通信速率和通信安全性，提出了一种基于声学参量阵的水声通信系统设计方案，在传统水声信道模型的基础上，对水声参量阵的信道模型进行建模和仿真分析。通过仿真分析表明，该水声通信系统在理论上能有效的提高水声信道质量，提高水声通信系统的抗干扰能力和速率。

参量阵；水声通信；多途效应；抗干扰；通信速率

由于电磁波在水中的衰减系数较大，而声波作为非电磁波能够实现水下远距离传输。因此，水下通信主要是水下声波通信[1]。国内外对于水声通信的研究已经投入了大量的资源和时间，目前水下通信系统取得了一定的发展和进步，但是仍然存在着诸多理论与技术问题，主要体现在：水声信道时变多径传播特性、水声信道特有的能量吸收特性和衰减影响、载波带宽极其有限等问题是限制水声通信技术向高速、高稳定通信系统发展的技术瓶颈。利用参量阵的超声波原频信号的高指向性避免信道的多途效应，根据参量阵差频信号具有的指向性和低频信道特性实现调制信号有效传输，在有限带宽的水声信道中充分利用信道空间资源能够为水声系统的发展提供一种有效的途径。

文中将在射线理论基础上利用信道-多途比（Signal-Multipath Ratio SMR）作为衡量信道质量的指标，分析普通水下声源的通信信道情况，再利用水声参量阵指向性特性，并通过水声参量阵的理论模型对参量阵水声信道的质量进行仿真分析。

1 浅海水声通信系统信道质量分析

海洋水声环境中，声速大小呈现垂直方向分层分布，其分布函数主要与海水温度、盐度、压力等因素有关，声波在传播过程中不同声速层之间发生折射现象，并满足Snell定律，使声波路径朝向声速大的方向弯曲。但是当今水声通信主要集中在浅海中进行，并且浅海环境比深海环境更加复杂（深海环境稳定，受波浪、船舶、潮汐等影响小），故文中主要针对浅海水声环境进行分析，声速为定值，并把声线当作直线处理[2]。

声波在海洋中存在海面和海底的反射以及海洋不同垂直分布层之间的折射，使得海洋信道不是单途信道而是多途信道。如果将海面和海底都看作平滑表面，声波在不均匀海洋介质中将产生稳定的多途信号。通过实际试验测量得到图1所示[3]，发现多途信号的理论预测和实际测量具有极大的相似性，说明利用理论模型（射线理论）是可以预测多途结构。在已知声速-深度分布曲线时，可用射线理论来预测水声信道结构，能够有效和清晰的解决海洋中的声传播问题[3]。

图1 多途信号的理论预测和实测波形

由于多途信号间的干扰，式中接收信号幅度会随着频率的变化而起伏。信道系统接收的信号可以表示如式（1）[4]：

式中an（t）表示t时刻第n个路径的信号衰减因子，τn（t）表示第n个路径的信号延时。其中具体传输函数为s（t）=Re [sl（t）ej2πfct]，sl（t）是对应的基带低通信号函数，fc表示信号载波频率，将s（t）代入公式（1），则接收低通信号的幅度函数可等效为：

式中sl（t）是对应的低通函数也可以由时变脉冲响应函数来等效：

对于连续变化的信道，脉冲响应函数的求和可转换成对时间τ的积分，即：

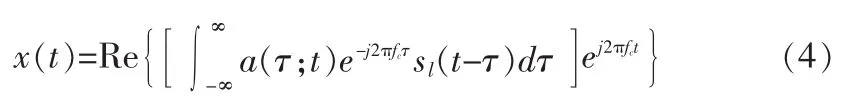
其中a（τ；t）是表示在延迟时间τ和时刻t时信号的衰减因子，可以看出上式积分代表信号sl（t）与等效低通时变脉冲响应c（τ；t）的卷积，从公式（4）分离出c（τ；t）可得：

公式（5）可被看作是连续多途信道对低通信号的信道脉冲响应函数，而公式（3）是对离散多途信道的脉冲响应函数。当fc作为未调制载波传播时，对所有时刻t，sl（t）=1，因此多途信道的等效低通接收信号为：

从公式（6）可以看出多途信道中在时刻t接收的信号是由一系列信号幅度为an（t）和相位角为θn（t）的矢量信号组成。对于an（t）和θn（t）是关于时间的函数，当信道介质参数不随时间变化，收发两端的位置是固定不变时，an（t）和θn（t）可以写成于an和θn的形式，此时我们可以得到信道的确定性模型。但实际上海洋信道是时变信道，所以上述两个参量都是时变函数，其中an（t）受到海洋内波的影响而有一些微弱的波动，但是θn（t）在不同延时τn（t）到达接收端时有不同的相位值，而且变化波动较大，对于时变信道特性只能通过对信道中介质的起伏强度以及均匀对的变化统计来得到信道的统计模型。

为了衡量水声信道的质量，在海况（包括海洋水中、海面和海底的情况）、海深、声速分布、信号频率、发射器深度等条件不发生明显变化的条件下，将信号-多途比（SMR）作为衡量参数，建立模型及仿真结果并由SMR数值来反应信道情况[5]。多途信道传播的确定性模型原理主要是海面和海底等边界的反射，导致了发射、接收机之间的多条路径，接收器接收到各种不同路径的信号，每条路径根据各自的信道有不同的延迟，因此浅海水声通信信道模型图如图2所示[6]：

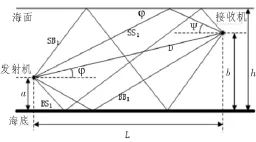
图2 浅海水声信道模型

（a:发射机到海底的距离；b:接收机到海底的距离；L：发射机与接收机的水平距离；h：海洋深度；φ：掠射角 ；ψ：入射角）

在声速为1 500 m/s定值、海洋表面反射由瑞利参数确定[7]、只考虑小掠射角（小于5°）并把海底反射系数近似为0.9的条件下，将水声信道的声线分为5大类不同类型的路径，并对该水声信道的进行几何求解得出基于射线理论的接收信号表达式。

浅海信道模型中将路径归纳为5大类型：D直达路径、SSn表示第一次和最后一次反射皆来自于海面的信号路径、SBn表示第一反射来自海面和最后一次反射来自海底的信号路径、BSn表示第一反射来自海底和最后一次反射来自海面的信号路径、BBn表示第一次和最后一次反射皆来自于海底的信号路径，其中n代表信号被反射的次数。图2所示为反射一次的情况，即n=1。为了能方便计算各路径的长度和延迟时间，通过发射端和接收端的镜像虚源可以画出并求出信道的直线，将不同镜像后虚源点发出的信号进行求和就是最终的多途信号，而直达信号的时间可以直接计算得到，多途信号的求和必须满足文献[8-9]中的边界条件。

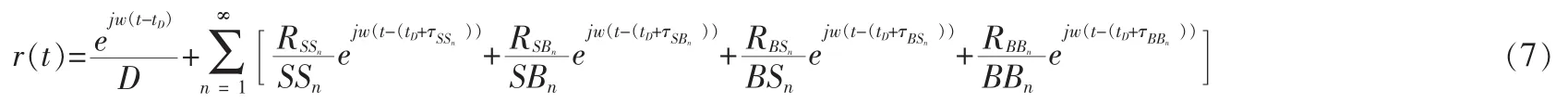
对图2所示信道模型性几何求解得出接收机信号表达式[10]：

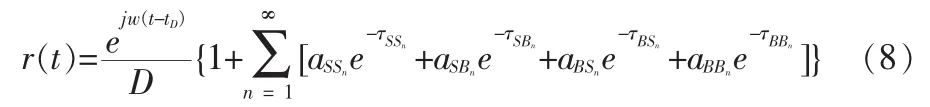
根据文献[6]定义自多途S信号和多途强度M的表达式为：

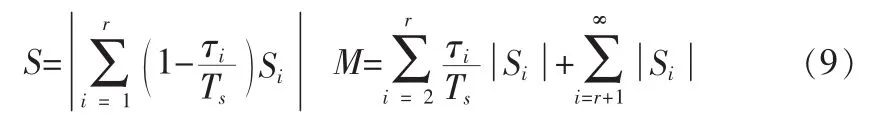
其中Si=aie-j2πfτi，Ts为原码信号时间宽度，r表示多途信号叠加的数量。水声信道的质量指标信号-多途比（SMR）便由原码元时间宽度Ts的信号S与互多途信号M的比值：

综合之前所述内容进行MATLAB仿真[11]：

浅海信道的自多途信号S和多途信号M的仿真结果如图3所示，具体参数：码元速率100 bps、测试范围20 km、载波频率15 kHz、风速10节、海底反射系数rb为0.9、声速为1 500 m/s、海水深度20米、发射端离海底15米、接收端离海底10米，仿真中拟定最大的反射次数为n=10。

根据仿真结果可以看出，利用普通声源进行水声通信，收发距离小于4 km时，多途号S相对多途信号M较弱，引起较大的码间干扰；当水平距离较远时，SMR呈上升状态，即多途信号M在传播过程中的衰减较大。

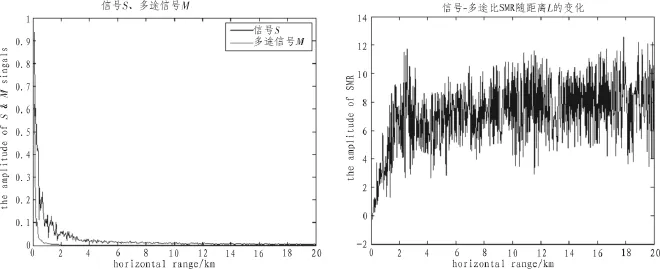
图3 浅海水声信道信号-多途比

2 参量阵水声能量分布特性

参量阵通过超声波换能器将调制后的信号发射到媒介中，传统的参量阵超声波的发射单元有的是均匀连续的，有的却是离散的，而换能器的形状也是多种多样，有圆形，矩形，六边形等，为了从理论上计算方便，下面将使用圆形均匀的超声波换能器进行分析。参量阵的低频声波是由于高频声波在介质中的非线性效应而产生的，而对于高频声波声场，非线性效应使得能量从基频转移到其他频率成分上，而这部分能量远远小于原波基频本身的能量，故在对参量阵声场进行仿真时，可以忽略非线性效应，而只考虑吸收与衍射效应，即仅在线性声学的范围内进行研究[12]。文中利用文献[12]中提出的方法，利用Hankel变换公式对波动方程进行改写和转换，在点（r，z）的声压表达式为：

其中一般圆形活塞源参量阵参数φ的计算公式：

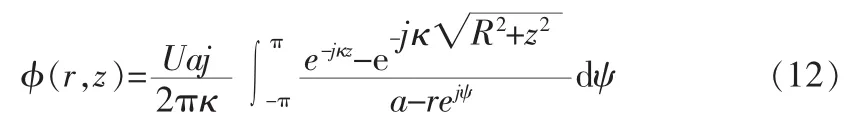
公式（12）中，U是信号幅值，k和αL分别为差频声的波数和吸收系数。假设在声场中，参量阵，参量阵原波需要传播一定距离后才会产生差频可听声信号，即源平面上没有差频信号，初始差频声压为0，即q（r，0）=0。这样，在求值过程中，可以通过先固定半径的值，对传播不同距离的差频声声压进行计算，进而得到整个平面声压的分布情况。利用公式（11）对参量阵声压分布进行MATLAB仿真[14-15]：

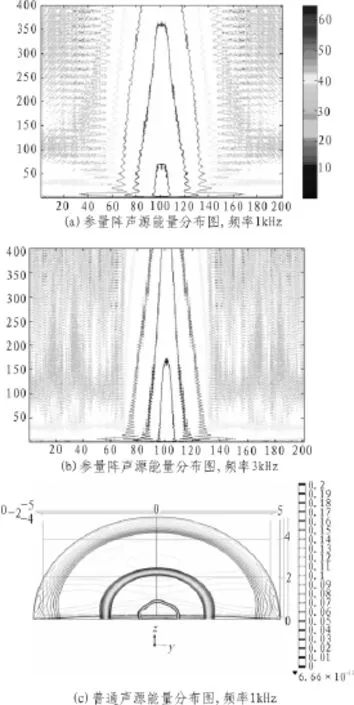
图4 参量阵声源和普通声源能量分布图

具体仿真参数：声速1 500 m/s，温度20℃，参量阵圆形半径为50 cm，空间范围是2×400 m。从仿真图里可以看出，水声参量阵轴向声压强度最大，即能量分布主要集中在参量阵轴向方向。而其他偏角的声压分布很小，即能量分布较弱，轴上最大声压比周围平均声压高20 dB左右。从等值线可以看出，水声在传播过程中，声束称锥形分布，并有一个波动的衰减过程。其中图4（a）是1 kHz差频信号的能量分布图，图4（b）是3 kHz差频信号的能量分布图。可以发现，差频频率越高，波束越细，能量越集中，指向性越好。但是综合上面两次仿真都可以看出，水声参量阵的能量分布主要集中在轴向方向，同时能量分布具有较高的一致性和指向性，其他偏角的能量分布较低。这对于普通全向水声声源来讲，换能器正向面成球面均匀分布，换能器正向轴能量与其他偏角方向的能量并没有太大的差距，这也是多途效应的信号根源。

3 参量阵水声通信系统信号-多途比分析

由于参量阵具有较高的指向性能量分布，能够较高的集中在轴向方向进行水声传播，极大的减少了其他偏角的信号强度，从多途信号的根源上对信号进行了一次衰减。这一特性也是参量阵水声同抑制多途干扰，提高信号-多途比的理论基础。

对于公式（8）。利用水声参量阵的能量分布，可以发现：参量阵的多途信号M由于能量分布的减少，在传播过程中对信道的多途干扰明显减弱。此时，接收信号函数表达式为：

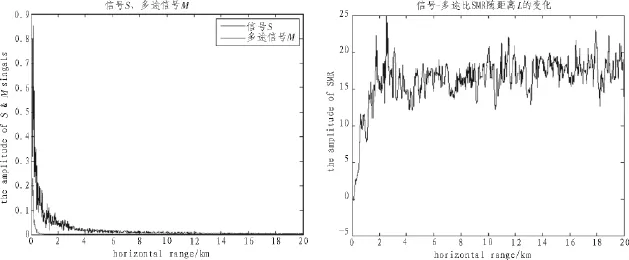
图5 差频400 Hz（15 kHz，15.4 kHz），阵元半径50 cm SMR随距离的变化图

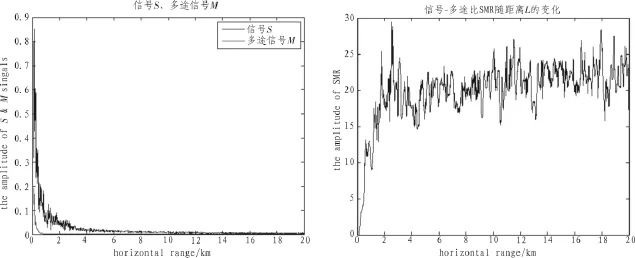
图6 差频1 kHz（15 kHz，16 kHz），阵元半径50 cm SMR随距离的变化图

其中多途信号M的衰减系数变为an′=an·ζ，ζ表示与普通声源相比，其初始声压的衰减系数，由参量阵的初始能量分布决定。通过计算出参量阵圆柱体内声压强度值和其他偏角的声压强度平均值的比值，利用该值对多途信号M的初始衰减系数进行近似估算。

对于普通声源，其声场分布呈球形均匀分布，即普通声源声压关系近似为A0∶A1=1∶1，参量阵锥形分布的声场中A0∶A1≠1∶1，求出A0和A1能近似求出其他偏角方向幅度衰减系数ζ。现定义ζ的近似估算公式如下：

其中，A0为参量阵圆柱面平均声强，A1为参量阵其他偏角方向平均声强，利用公式（13）进行仿真可以计算求得。利用参量阵的能量分布仿真和射线理论接收信号函数，进行参量阵水声信道的SMR分析。水声参量阵信道的自多途信号S和多途信号M的仿真结果如下图所示，具体参数：码元速率100bps、测试范围20 km、参量阵阵元圆形半径25 cm，载波频率15 kHz、风速10节、海底反射系数为0.9、声速为1 500 m/s、海水深度20米、发射端离海底15米、接收端离海底10米，仿真中拟定最大的反射次数为n=10。

根据仿真结果图5、图8可以看出，与普通水声信号声源相比，M信号的初始信号明显衰减很多，而信号S的归一化幅度有明显的增大，整个参量阵信道的SMR数据比普通声源的SMR在数值上高20 dB左右。在较短距离内，锥形分布的平均声压级差距并不明显，即多途信号M的衰减相对较弱，但整体上SMR上升趋势更加快速，平稳。在中远距离内，SMR的波动相对普通声源较小。在同样参量阵声源尺寸情况下，差频信号越高，SMR上升速度越快，多途信号M的初始幅度越小；在同样差频信号情况下，参量阵声源尺寸越大，自多途信号S的归一化幅度越大，SMR的上升速度越快。主要因素有：差频信号频率越高，其能量指向性越好，多途信号M越弱，减少了多途信号对信道的多途干扰；此外，参量阵阵元尺寸越大，参量阵的指向性越好，信号S的幅度越高，多途信号M的初始幅度衰减更加严重。在中距离范围内，对SMR产生影响的主要是环境噪声的影响，故出现一定的波动。

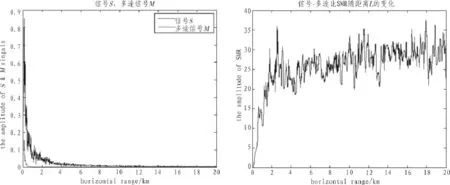
图7 差频400 Hz（15 kHz，16 kHz），阵元半径25 cm SMR随距离的变化图

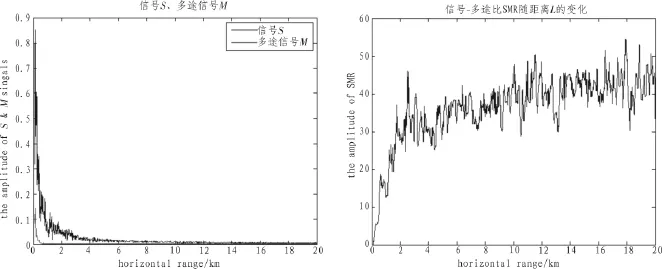
图8 差频1 kHz（15 kHz，16 kHz），阵元半径25 cmSMR随距离的变化图

4 结 论

利用参量阵发射技术进行水声通信实现低频远程传输，通过其窄指向性的特点提供了一种抑制多途效应方法。对于普通低频声源，低频声信号吸收衰减较小，适合远程传播，但是普通低频声源基阵孔径的限制，低频换能器难以形成具有空间指向性的声束进行传输，不但多途效应显著影响通信质量，而且污染了环境声场对其他水声设备造成干扰，并且容易被截获不利于通信安全。水声参量阵发射高强度的高频载波，在原高频波束宽度内通过介质的非线性作用，自解调产生低频声波，可以在小尺寸发射阵下实现窄波束定向发射低频声波信号，而且波束无旁瓣有良好的聚焦性。利用此特点能为抑制来自海底海面的相干多途干扰，并根据方位信息针对接收端定向发射，减少对其他方向上的水声设备的干扰，同时增加通信隐蔽性和安全性提供了有效的解决方案。

利用参量阵技术方便实现低频宽带发射，提供了一种提高水声通信可用的带宽范围和实现通信速度提高的途径。利用水声参量阵的定向性和无旁瓣特性能够在空间上避免对其他水声设备的干扰，对参量阵信道进行并行处理安置，充分利用空间，实现水声的并行通信，提供了一种在有限带宽资源的情况下提高通信速度的方法。参量阵能够将高频段较窄的绝对带宽的高强度声波，通过非线性作用转化成低频声波，保证低频水声波束绝对带宽的不变，实现低频带宽声波的发射。

基于参量发射阵的水声通信系统的低频窄波束、宽带、基阵尺寸小、波束无旁瓣等技术特点、能有效地克服常规水声通信带宽窄、速率低、浅海多途效应显著、误码率高等不足，具备在浅海环境中实施高速率远程水声通信的能力。

[1]汪德昭，尚尔昌．水声学[M]．北京：科学出版社，1981．

[2]杜功焕，朱哲民．声学基础[M]．南京：南京大学出版社．2012．

[3]侯自强.声呐信号处理原理与设备[M].北京：海洋出版社，1986.

[4]Urick R J.Principles of underwater sound[M].3 rd edition. New York:McGraw-Hill，1983.

[5]Brekhovskikh L M.Waves in Layered Media[M].1st edition. New York:Academic Press，1960.

[6]刘伯胜，雷家煜.水声学原理[M].哈尔滨:哈尔滨工程大学出版社，1993.

[7]郭长勇.浅海多途水声信道通信仿真研究[D].厦门：厦门大学，2002.

[8]Christian Bjerrum-Niese，René Lützen.Stochastic Simulation of Acoustic Communication in Turbulent Shallow Water[J]. Oceanic Eng.，2000，25（4）：523-532.

[9]Berktay H O.Possible Exploitation of Non-Linear Acoustics in Underwater Transmitting Applications[J].Sound Vib，1965，2（4）:435-461.

[10]Liauh C T，Lin W L.Fast numerical scheme of computing acoustic pressure fieldsforplanarcircularultrasound transducers[J].Acoust.Soc.Am，1999，105（4）:2243-2247.

[11]陈敏，徐利梅，黄大贵，等.基于MATLAB的换能器阵列指向性分析方法研究[J].电声技术，2006（5）：25-28.

[12]肖永龙.控距参量声源的研究与实现[D].成都：电子科技大学，2014.

[13]陈敏.声频定向系统理论与关键技术研究[D].成都：电子科技大学，2008.

Analysis of underwater acoustic communication channel based on parametric array

LI Lun，CHEN Min，YUAN Shou-xing，HU Lun-chuan
（School of Aeronautics and Astronautics of UESTC，Chengdu 611731，China）

In order to restrain the multipath interference in the communication of underwater acoustic，enhance the antiinterference ability of the underwater acoustic communication system，enhance the communication rate and security，a design of underwater acoustic communication system based on acoustic parametric array is proposed.The simulation analysis shows that the underwater acoustic communication system based on parametric array can effectively improve the quality of the underwater acoustic channel and improve the anti-interference ability and the Ratio of underwater acoustic communication system.

parametric array；underwater communication；multipath-interference；anti-interference communication rate

TN929.3

A

1674－6236（2016）24-0127-05

2015-12-08 稿件编号：201512092

李 伦（1990—），男，四川自贡人，硕士研究生。研究方向：声学参量阵、水声通信技术。