Shadow仿人灵巧手动力学研究

靳 果，邱兵涛，韩 枫

（1.河南工业职业技术学院 河南 南阳473000；2.中国人民解放军65555部队 辽宁 海城114200）

Shadow仿人灵巧手动力学研究

靳 果1，邱兵涛1，韩 枫2

（1.河南工业职业技术学院 河南 南阳473000；2.中国人民解放军65555部队 辽宁 海城114200）

为了实现对仿人灵巧手的实时控制，需要对灵巧手的动力学逆问题进行研究，得到运动轨迹相关参量与所需力矩的关系。本文以Shadow仿人灵巧手为研究对象，参考灵巧手运动学的研究结论，建立动力学模型，分析Shadow仿人灵巧手的手指连杆动力学、腱传动系统动力学和驱动系统动力学相关问题，最后得到仿人灵巧手单指动力学方程，为灵巧手的仿真实验和实际应用提供了理论基础。

灵巧手；动力学；逆问题；动力学模型；动力学方程

仿人灵巧手应用于中医按摩领域，对手部的“灵巧性”有很高的要求，机器人动力学逆问题的研究旨在改善机器人控制系统工作的稳定性和控制精度，实现对灵巧手的最优控制[1]，达到良好的动态性能和最优指标。

文中研究的对象是Shadow仿人灵巧手（英国Shadow公司），借助灵巧手运动学研究的结论[2-3]，建立动力学模型，根据灵巧手轨迹运动对应的关节角位移、角速度和角加速度，推导出完成运动所需要的关节力矩，建立运动过程和力矩的关系，并得到仿人灵巧手的单指动力学方程。

1 Shadow仿人灵巧手介绍

研究中采用的Shadow仿人灵巧手具有24个关节20个自由度，拇指采用5关节手指结构，共5个自由度；中指、食指和无名指采用4关节手指结构，各3个自由度；小指与中指的结构和尺寸相似，另外单独设计了一个掌骨关节，共4个自由度，如图1所示。

Shadow灵巧手通过40根气动肌肉（Air Muscle）驱动，利用腱传动，力和力矩由各关节传递到手指和指端，实现运动和动力的远距离传送，采用集成的关节位置传感器、压力传感器、指尖触觉阵列传感器。

图1 Shadow灵巧手结构简图

2 手指动力学分析

手指动力学主要研究驱动手指关节所需的力矩与关节运动过程中的角位移、角速度和角加速度之间的关系。由于各手指结构相似，以中指为例研究单个手指的动力学特性，中指的结构如图2所示。

2.1 仿人灵巧手动力学模型

仿人灵巧手单指动力学的研究，需要建立对应的动力学模型，Shadow仿人灵巧手中指动力学由三部分构成：手指连杆动力学、腱传动系统动力学和驱动系统动力学[4]。

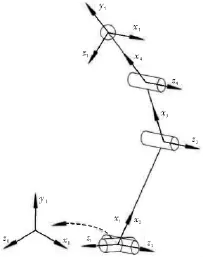
图2 Shadow灵巧手的中指结构

1）中指连杆动力学

连杆动力学主要确定中指各关节的驱动力矩与关节运动情况之间的关系，本论文采用牛顿-欧拉（Newton-Euler）法推导中指的连杆动力学方程。

2）腱传动系统动力学

腱的刚度、系统的摩擦和阻尼等因素对腱传动系统的静态和动态特性具有一定的影响。研究发现，重量轻、刚度大、长度短的腱在传递力和速度方面效果更优秀[5]。

3）驱动系统动力学

Shadow灵巧手所采用的Mckibben型PMA为编织网纤维缠绕结构，具有一个封闭的弹性容腔，充气后膨胀，迫使外层编织网产生位移和力的输出。

2.2 中指的连杆动力学分析

中指连杆动力学的逆问题推导采用迭代的Newton-Euler算法，第一步，利用连杆运动学完成连杆1到连杆4的外推迭代，得到所有连杆的线速度、线加速度和角速度、角加速度，利用Newton方程和Euler方程计算连杆受到的惯性力和力矩；第二步，利用连杆间力的平衡关系完成连杆4到连杆1的内推迭代，得到每一个关节所需的驱动力矩。

封闭形式的Shadow灵巧手中指连杆动力学方程为[6-9]：

式（1）中，τ—中指的连杆驱动力矩向量，τ=[τ1τ2τ3τ4]T；q—关节角位移向量，q=[θ1θ2θ3θ4]T；—关节角速度向量，；—关节角加速度向量，；D（q）—中指惯性矩阵，是4×4的正定矩阵，D（q）表示惯性力（矩）；h（q，）—离心力和哥氏力向量：关节离心力与成正比，哥氏力与·成正比；G（q）—重力矢量。

另外，系统的摩擦因素——主要是粘滞摩擦τv和库仑摩擦τμ，即：，其中，v是粘滞摩擦系数，μ是库仑摩擦系数，Nf是正压力。

编号i的连杆总摩擦τfi可表示为：

将摩擦因素加入到系统中，则仿人灵巧手中指动力学方程的表述为：

式（3）中，τf—连杆摩擦力矩向量，τf=[τf1τf2τf3τf4]T

2.3 腱传动系统动力学分析

Shadow仿人灵巧手依靠腱结构实现动力传送，腱的一端固定在连杆上，另一端固定于驱动器——PMA末端，每个腱仅与一个连杆相联，并且由一个PMA控制，如图3所示。一个自由度需要两组腱和PMA完成控制，如图4所示，中指具有3个独立自由度，需要6组腱和PMA，完成运动和动力的传送[10]。

图3 Shadow灵巧手的腱结构

图4 腱控制关节示意图

中指的两个远端关节利用腱构成耦合结构，耦合关节具有一个独立的自由度，减少了驱动器的数量，如图5所示。

图5 耦合关节

根据Shadow灵巧手腱结构质量轻、惯性负载小、摩擦小、成本低、耐用性强的特点，简化腱传动系统动力学模型：每个关节只存在关节变量；腱轻质、无弹性；腱与关节相切接触；无摩擦。

每个腱的位移量hj为关节角位移的线性函数[11]：

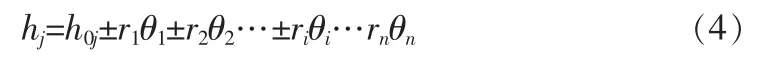
式（4）中，h0j—关节角位移q=0时腱j的初始位移量，Δhj= hj-h0j；θi、ri—第i个关节处的关节角度和滑轮半径。当转角为正时，式中的符号取决于腱是伸长还是缩短。

利用能量守恒——腱所做功等于手指所做功得到：

式（5）中，τ—关节力矩向量；Δq—角位移变化向量；Δh—腱位移变化向量，Δh=[Δh1Δh2Δh3Δh4Δh5Δh6]T；f—腱张力向量，f=[f1f2f3f4f5f6]T。

还可得：

2.4 驱动系统动力学分析

Shadow仿人灵巧手的动力系统采用Mckibben型PMA：内部为橡胶管，外面是纤维编织网，两端用金属箍固定。当橡胶管由于充气膨胀时，外层纤维编织网被撑起，产生轴向收缩力，如图6所示。

图6 PMA驱动形式

对Mckibben型PMA的描述普遍采用下述数学模型[13-15]：

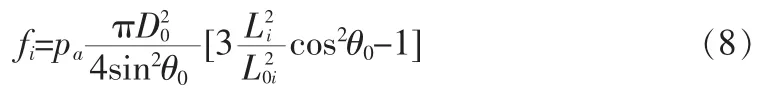
式（7）中，fi—编号i的PMA的收缩力；pa—充气压力；D0—初始直径；θ0—纤维网与轴向的初始夹角；L0i—初始有效长度；Li—变化后的长度。

腱无弹性，因此腱的位移变化与PMA的长度变化相等[16]，即：Δh=L0-L，可得：

式（9）中，L—人工肌肉变化后的长度向量，L=[L1L2L3L4L5L6]T；L0—人工肌肉初始长度向量，L0=[L01L02L03L04L05L06]T。

2.5 中指动力学方程

根据机器人学理论，手指受力的静力学模型[3]：即：

其中，τ—各关节的输出力矩向量；J—手指的雅克比矩阵；fext—指尖与外界环境的接触力矢量。

综合式（3）、式（6）、式（8）和式（10），得到Shadow仿人灵巧手中指动力学方程[4，11]：

式（9）、式（11）描述了PMA伸缩量与各关节角位移之间的关系。

3 结 论

文中首先建立了Shadow仿人灵巧手的中指动力学分析模型：1）手指连杆动力学，2）腱传动系统动力学，3）PMA驱动系统动力学。然后，利用迭代的Newton-Euler算法推导出单指的手指连杆动力学方程，利用腱传动理论推导出手指关节转矩与传动腱张力之间关系，利用PMA气动人工肌肉模型推导出PMA收缩量与输出力之间关系，最终得到具有连杆结构、由PMA驱动、腱传动的Shadow仿人灵巧手的单指动力学方程，建立了手指各关节运动参数（角位移、角速度、角加速度）、PMA收缩量以及手指所受外力之间的关系。

[1]熊有伦，唐立新，丁汉，等.机器人技术基础[M].武汉:华中科技大学出版社，1996.

[2]张鹏程，张铁.基于矢量积法的六自由度工业机器人雅可比矩阵求解及奇异位形的分析[J].机械设计与制造，2011（8）:152-154.

[3]靳果，赵冉，韩枫.五自由度仿人灵巧手运动学研究[J].电子设计工程，2014，22（24）:86-89.

[4]姜力，蔡鹤皋，刘宏.新型集成化仿人手指及其动力学分析[J].机械工程学报，2004，40（4）:139-143.

[5]Johnstun C R，Smith C C.Modeling and design of a mechanical tendon actuation system[J].Transactions of the ASME Journal of Dynamic Systems，Measurement，and Control，1992，114（2）:253-261.

[6]余麟，刘昊，彭光正.五指仿人灵巧手运动学与动力学模型[J].北京理工大学学报，2008，28（10）:880-884.

[7]王洪瑞，吕应权，宋维公.BH-1灵巧手运动学和动力学建模研究[J].系统仿真学报，1997，9（3）:44-50.

[8]郑显华，刘新华，张霖，等.基于Adams的仿人机械灵巧手动力学仿真分析研究[J].制造业自动化，2013，35（14）:147-149.

[9]郭卫东，满洁，张玉茹.灵巧手的单指动力学方程建立与验证[J].机械设计，2002，19（4）:13-14.

[10]LIU Hao，FAN Wei.Study on a new dexterous hand actuated by pneumatic muscle actuators[C]//Proceedings of the 7th JFPS International Symposium on Fluid Power，TOYAMA，2008:521-526.

[11]理查德·摩雷（Richard M.Murray）等.机器人技术的数学导论[M].徐卫良，钱瑞明，译.北京:机械工业出版社，1998.

[12]刘世廉，宋金泽，马宏绪.基于腱传动的仿人型多指机械手的简易设计[J].电子机械工程，2004，20（1）:57-59.

[13]彭光正，余麟，刘昊.气动人工肌肉驱动仿人灵巧手的结构设计[J].北京理工大学学报，2006，26（7）:593-597.

[14]田社平，林良明.人工肌肉静态特性及其测量[J].实用测试技术，1998，24（6）:12-14.

[15]刘小华.McKibben气动人工肌肉的静态特性及预紧力研究[D].兰州：兰州理工大学，2010.

[16]刘昊.气动肌肉驱动灵巧手的结构设计与控制方法研究[D].北京：北京理工大学，2011.

Dynamics research of Shadow dexterous hand

JIN Guo1，QIU Bing-tao1，HAN Feng2
（1.Henan Polytechnic Institute，Nanyang 473000，China；2.65555 PLA Troops，Haicheng 114200，China）

In order to to realize the real-time control of dexterous hand，the researches of the inverse problem of dynamics of dexterous hand are needed，so that the relationship between motion locus parameters and the required torque can be obtained. In this paper，the Shadow dexterous hand was studied，and the research conclusion of kinematics was referred to.By establishing the dynamic model，the dynamics of Shadow dexterous hand was studied in three respects:the finger link system，tendon transmission system and pneumatic muscles actuator.Finally the single finger dynamics equation of dexterous hand was derived.

dexterous hand；dynamics；the inverse problem；dynamical model；dynamics equation

TN609

B

1674－6236（2016）24-0102-03

2016-01-13 稿件编号：201601091

靳 果（1985—），男，河南南阳人，硕士研究生，助教。研究方向：电子信息工程。