Sum-Product Networks模型的研究及其在文本分类的应用

李 俊

（1.中国科学院 上海微系统与信息技术研究所，上海 200050；2.上海科技大学 信息科学与技术学院，上海 201210；3.中国科学院大学 北京 100049）

Sum-Product Networks模型的研究及其在文本分类的应用

李 俊1，2，3

（1.中国科学院 上海微系统与信息技术研究所，上海 200050；2.上海科技大学 信息科学与技术学院，上海 201210；3.中国科学院大学 北京 100049）

图模型在机器学习有着广泛的应用。相比图模型，Sum-Product Networks模型具有更强表达能力和更快的推理速度，所以其在对文本和图像数据建模有着广泛的应用。本文总结Sum-Product Networks这一新的深度概率模型的研究进展，先介绍了固定结构的Sum-Product Networks的参数学习方法，再介绍了根据不同的输入数据而进行的结构和参数学习方法。并且介绍了判别式和生成模型的Sum-Product Networks，最后介绍了Sum-Product Networks在文本分类上的应用。

Sum-Product Networks模型；概率模型；数据挖掘算法；文本分类

随着信息社会的发展，互联网上的信息爆炸式的增长，如何有效地处理和组织这些数据，成为当前研究的重要课题。图模型常常被用来对大数据建模，它可以简洁的表示变量的概率分布，并且可以高效的计算和精确的学习模型的参数。一般情况下，我们常常使用图模型来简洁的表示复杂的分布，但是它在参数学习和推理的时候比较困难，这是由于它在归一化的时候需要比较大的计算量。而且图模型在做推理的时候，最坏的情况下会有指数级别的复杂度。另外随着变量的增加，图模型的复杂度会越来越高。深度架构[1]可以看成一个有着多层隐变量的图模型，而且很多的分布只可以用深度网络来表示。然而在混合一些非凸的似然估计和比较高复杂度的推理让学习这种深度网络非常的难。而图模型虽然在推理上是可处理的，但是其在简洁表征方面的性能是非常有限的。

而Sum-Product Networks具有很强的表达能力和快速的推理能力。在2011年，Poon和Domingos提出了Sum-Product Networks，通过增加层数来提高表达能力并且可以非常高效的做推理[2]。SPN可以看成是一个广义的有向无环的混合图，SPN中间层一种小的由product节点和加权的sum节点的SPN结构不断递归的组成的，而最下面的叶子节点是各个单一变量。Sum节点可以看成变量在集合上的混合，而product节点可以看成特征的混合。SPN可以看成概率上下文无关文法的特例，它有着很好的处理能力和很强的表达能力，这使得SPN有着很广泛的应用，特别是一些视觉应用中。

1 Sum-ProductNetworks介绍

SPN可以表示为一个有根节点的有向无环图。在这个有向无环图里面：叶子节点是不同分布的单变量。一个有着变量X1，X2，X3，···，Xd的sum-product network（SPN），其叶子节点（终节点）是X1，X2，X3，···，Xd，和，···，，SPN里面的非终节点是sum和product节点。SPN中sum节点i和子节点j连接的边有一个非负的权值Wij，所以SPN中sum节点的值是ΣWjWij，其中Vj代表第j个节点的值，SPN中product节点的值表示为孩子节点值的乘积。如图1，这是一个根节点是sum节点SPN结构，根节点与下面的各个product节点分别以0.5，0.2，0.3的权值连接，通常product节点和sum节点在每一层交替出现，product节点下面一层均为sum节点，sum节点在与带不同权值的叶子节点X1，X2，，相连。SPN性质：一个容易处理的单一分布是一个SPN，一些有着不相交scope的SPN的乘积仍然是一个SPN；一个以i为根节点的子SPN表示在该i节点下scope的分布；一个SPN的scope代表变量出现的集合。当一个sum-product network中sum节点的孩子有着相同的scop，则这个SPN是完全的；当一个sumproduct network中product节点下面的孩子节点变量和其他孩子的节点变量没有相反的，则说这个SPN是一致的；一个SPN是完全的并且一致的则该SPN是有效的。SPN中的子节点作为根节点时所覆盖的子网络也是一个SPN。我们可以将一个 sum-product network用 变量 X1，X2，X3，···，Xd，和···，表示成S（X1，X2，X3，···，Xd，，···，），其中（例如Xi=1则=0，或者Xi=0则=1）。当把所有的变量设为1，可以将其表示为S（*），S（*）=S（1，1，1，1）。S（x）的值定义为一个对已变量x未归一化的概率分布。如图S（X1，X2，，）=0.5（0.6X1+0.4）*（0.3X2+0.7）+0.2（0.6X1+0.4）*（0.2X2+ 0.8）+0.3（0.9X1+0.1）*（0.2X2+0.8），所以网络的多项式系数是（0.5*0.6*0.3+0.2*0.6*0.2+0.3*0.9*0.2）X1X2+···。

图1 SPN的结构

2 Sum-Product Networks的发展

SPN的发展主要围绕着怎么学习这个SPN结构。对于SPN学习问题，我们可以用生成式模型或者判别式模型的SPN对数据建模学习。生成模型是运用联合概率分布P（X，Y）来对数据建模，X是输入数据，Y是预测值，它的学习收敛速度更快；而判别式模型是运用P（Y/X）对数据建模，在处理分类和回归问题效果更好。对于生成模型的SPN，在2011年Poon和Domingos在一个固定结构的SPN结构上学习参数，他们提出了用在线hard EM算法来学习SPN。对于判别式SPN，在2012年Gens和Domingos在固定结构上学习SPN，并用来处理图像来分类问题，他们使用Back Propagation的梯度下降的算法来学习SPN结构中的参数，并且取得了很好的分类效果，但是他们面临着权衡SPN灵活性和学习SPN开销的问题[3]。

对于不固定结构SPN的结构学习问题，在2012年Dennis和Ventura提出了对SPN的结构的学习，但是有很多的局限性。该SPN学习方法在一系列分层结构中让变量聚类，并且这些聚类在一起的变量，在在相似的样本里面有相似的数值，这使得依存关系很强的变量有比较多的减少（使得似然估计的损失减少）。在该SPN中，在一个区域中sum节点的数量不是可以学习得到的，而是固定的一个输入参数。这个SPN学习算法是很复杂的，而且不能保证找到一个局部最优的似然估计，这也表明这种方法学到的SPN不是非常好的SPN。SPN和和积网络（一种算数网络，AC）[4]，与或图相关[5]。在2008年Lowd和Domingos[6]，和2010年Gogateetal[7]分别提出了一种和SPN相关而且很容易学习的模型，但是有着更加多的限制。Lowd和Domingos的算法在上下文无关的条件下，学习贝叶斯网络并使用网络的推理的代价当做正则项的惩罚。Gogat通过不断的递归搜索在近似独立的集合中拆分开的变量特征，来学习一个很高树宽的马尔科夫网络。在2013年RobertGens和PedroDomingos提出了第一个在不牺牲SPN表达能力的条件下，来学习SPN的结构的算法[8]。他们的算法并行的递归调用这些递归的结构。这个算法可以看做一个混合EM算法（学习sum节点）和图模型的结构学习（学习product节点）。但是这种方法学到的SPN的结构质量和所取得的似然估计不太好，里面有很多冗余的节点和子树。

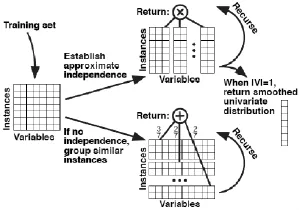
图2 SPN结构学习的递归调用算法

如图2所示，我们学习SPN的结构时候，输入的每个样本是用由一系列变量组成的向量来表示的，所有的训练样本构成一个矩阵。如果矩阵的列数（变量数）为一，则返回该单一变量的分布。如果可以将根据变量的独立性，将变量拆分成互相独立的子集合，则再用该算法递归的调用这些子集并且返回这些学到的子SPN的积（图2的上部分所示）。否则，将样本聚类到各个子集合里面，再在各个子矩阵中调用该算法，从而学习子SPN结构，最后再返回这些带权重的子SPN的和。Sum节点下面的权值代表着对应子SPN中样本的数量比例。如果变量不可以再分割，该算法返回一个完全分解的分布。在一种极端的条件下，如果在样本数量|T|=1之前，该算法总是不能找到互相独立的变量的子集合，该算法将返回分布的密度估计。在通常条件下，当样本数量|T|远远大于变量数量|V|的时候，该算法常会将样本集合进行拆分，当|V|远远大于|T|的数量的时候，该算法常会对变量集合进行拆分。这个算法对变量或者样本可以有不同的切分结果，最后都得没有条件独立而且容易处理的模型。

运用上面 Robert Gens的SPN结构学习算法，学习得到的SPN结构，观察发现里面有一些的节点是相同的，整个SPN结构有点冗杂，而且学习得到的SPN结构深度比较浅（较深的时候，能得到更强的表示）。对此，Vergari和Di[9]在原SPN学习算法上添加了一些限制条件：限制sum节点下面孩子节点的个数，bagging方法。限制sum节点下面孩子节点的个数，从而使得学到的SPN结构更加深，从而模型的表达能力得到提升，优化的参数也会减少，也提高其鲁棒性。bagging方法，在运用上述SPN算法对矩阵进行切割时，初始化时将原矩阵切分为几个子矩阵（即弱的学习算法）经过多轮训练，再进行投票组成一个子矩阵切分方法（强的学习算法），最后学习得到一个表达能力更强和推理速度更快的SPN结构。

图3 基于SVD分解的SPN结构学习

对于 Robert Gens的 SPN结构学习的一系列问题，Tameem和 David在 2015年提出了一种基于 SVD分解的SPN结构学习算法[10]。像2013年Robert Gens那样通过对矩阵进行切割来来学习SPN结构，通过在矩阵中提取一个rank-1的子矩阵来对原矩阵进行切割，其中求解rank-1的算法采用power method算法。如图，对于一个矩阵，找到了一个rank-1的2*2维子矩阵，这可以将切割为三个部分，按照行对矩阵切割得到两个SPN结构的sum，对列的切割得到SPN结构的product，在子SPN结构里面，不断重复这个过程，最终学习得到更好SPN结构。

3 评价方法

由于直接计算马尔科夫网络的似然估计不好处理，我们常用假似然估计（PLL），一种计算变量的近视联合概率分布的方法，来评价图模型的好坏。在训练的时候计算的PLL常被当成一种替代的似然估计。另外也有一些其他图模型来对数据建模：Della Pietra[11]和Ravikumar[12]的方法分别简称为DP和L1。L1结构学习是使用Andrew和Gao对L1逻辑拟合的提出的OWL-QN包[13]。使用假似然估计（PLL）来评价的实验表明，这两种常用的图模型均不如SPN。

另外一种评价方法是测试数据的推理能力，随机的从大量的测试样本数据中选取一定比例的询问和证实数据（例如，10%的询问数据q和30%的证实数据e）。对于一个选定的测试样本，一个询问P（Q=q/E=e）是按照比例随机的选择变量和其对应的值。最后记录给定证实的平均条件概率的log似然估计（CLL）。SPN可以在线性时间里面做准确的推理。而图模型是非常难做精确的推理，我们常用吉布斯采样来做近视的求解。SPN的推理速度和准确度远远好于图模型。

4 在文本分类的应用

2011年Poon和Domingos[3]提出了判别式SPN，并将其运用到CIFAR-10数据集的图片分类的问题上，并且取得了当时最好的分类效果。在2015年Tameem和David[10]提出了判别式SPN结构来对文本数据进行分类。假设分类的类别集合为C={1，···，n}。对于训练数据，在类别集合中的每一个类别上，使用基于SVD的方法学习得到一个SPN结构，然后再使用HSIC变换[14]，来提取和分类类别强相关的特征。再用一个sum节点将各个类别的SPN结构加起来，即得到一个sum节点混合的条件分布P（Z/Y=j），其中j∈C，其中sum节点下面的权值按各个类别上训练样本的数量比例来确定。从而对于不同的样本输入这个网络，可以的得到预测的类别。

Tameem和David选用了USPS[15]和MNIST[16]的数字手写体识别数据集来验证该方法的效果（均转化为文本数据，分十个类）。USPS这个数据集合每个图片是16*16的，所以数据集合中的每一个数字图片可以用一个256维的向量来表示，这个数据集中每个样本由256维的向量来表示，数据集有7 291个训练样本和2 007个测试样本；其中训练数据集每一个类别800个样本，测试数据集中每个类别中有300个样本。而MINIST数据集中每个样本由28*28的向量组成，训练数据集每一个类别有6 000个样本，测试数据集中每一个类别有1 000个样本。我们输入这些训练数据，可以学到一个SPN的网络结构，根节点代表预测的类别，在测试数据集上达到比传统分类方法更高的分类精度。

5 结束语

在机器学习、数据挖掘领域中，我们常需要运用概率模型来对数据建模。我们通常使用的图模型只可以简洁地表示完全概率分布，而Sum-product networks作为一种有着多个隐含层的概率模型，SPN还可以简洁的表示各种边缘分布。此外SPN有着更强的表达能力，还有更加快速和精确的推理能力。在未来处理具体的机器学习应用中，SPN会有着更加广泛的应用。

参考文献：

[1]Y.Bengio.Learning deep architectures for AI.Foundations and Trends in Machine Learning[J].2009：1-127.

[2]Hoifung Poon and Pedro Domingos Sum-Product Networks:A New Deep Architecture[C].Uncertainty in Artificial Intelligence 27.

[3]Robert Gens and Pedro Domingos Discriminative Learning of Sum-Product Networks[C].Advances in Neural Information Processing Systems，2012：3248-3256.

[4]Darwiche，A.A dierential approach to inference in Bayesian networks[J].Journal of the ACM，2003，50（3）:280-305.

[5]Dechter，R.Mateescu，R.AND/OR search spaces for graphical models[J].Artificial intelligence2007，171:73-106.

[6]Lowd，D.and Domingos，P.Learning arithmetic circuits[C]. Uncertainty in Artificial Intelligence，2008.

[7]Gogate，V.，Webb，W.，and Domingos，P.Learning effcient Markov networks[C].Advances in Neural Information Processing Systems，2010，748-756.

[8]Gens，R.，Domingos，P.:Learning the structure of sumproduct networks In Proceedings of the 30th International Conference on Machine Learning[C].2013：873-880.

[9]Vergari，Antonio and Di Mauro，Nicola and Esposito，Floriana Simplifying，Regularizing and Strengthening Sum-Product Network Structure Learning [C].Machine Learning and Knowledge Discovery in Databases，2015：343-358.

[10]Tameem Adel，David Balduzzi，and Ali GhodsiLearning the StructureofSum-ProductNetworksviaan SVD-based Algorithm[C].Uncertainty in Artificial Intelligence，2015.

[11]Della Pietra，S.，Della Pietra，V.，and Laerty，J.Inducing features of random fields[J].Pattern Analysis and Machine Intelligence，IEEE Transactions on，1997（19）:380-392.

[12]Ravikumar，P.，Wainwright，M.J.，and Laerty，J.D.Highdimensional using model selection using L1 regularized logistic regression[J].The Annals of Statistics，2010，38（3）: 1287-1319.

[13]Andrew，G.and Gao，J.Scalable training of L1-regularized log-linear models[C].Proceedings of the 24th international conference on Machine learning，2007：33-40.

[14]A.Gretton，O.Bousquet，A.Smola，and B.Scholkopf.Measuringstatisticaldependence with Hilbert-Schmidt norms[J].In AlgorithmicLearning Theory，2005，37（34）:63-77.

[15]J.J.Hull.A database for handwritten text recognition research[J].Pattern Analysis andMachine Intelligence，IEEE Transactions on，1994，16（5）:550-554.

[16]Y.LeCun，L.Bottou，Y.Bengio，and P.Haffner.Gradientbased learning applied to document recognition [J].In Proceedings of the IEEE，1998，86（11）:2278-2324.

The development of Sum-Product Networks model and its application in text classification

LI Jun1，2，3
（1.Shanghai Institute of Microsystem and Information Technology，Chinese Academy of Sciences，Shanghai 200050，China；2.School of Information Science and Technology，ShanghaiTech University，Shanghai 201210，China；3. University of Chinese Academy of Sciences，Beijing 100049，China）

Graph model is wide used in the area of machine learning.Compared with Graph model，the model of Sum-Product Networks is more representative and faster than graph model，thus it is widely used to model text and image data.This paper firstly summarizes the research progress of Sum-Product Networks，new deep probability model，and then introduces the method of parameter learning with fixed structure of SPN and the method of structure learning based on different input data for Sum-Product Networks.At last，the paper introduces the application of discriminant Sum-Product Networks in text classification.

Sum-Product Networks model；probability model；data miningalgorithm；text classification

TP391

A

1674－6236（2016）24-0042-04

2015-12-25 稿件编号：201512259

李 俊（1990—），男，湖南邵阳人，硕士。研究方向：信号与信息处理、机器学习，数据挖掘。