一种自适应广义空间调制及其低复杂度算法

刘健伶,陈志刚,王磊

(西安交通大学电子与信息工程学院, 710049, 西安)



一种自适应广义空间调制及其低复杂度算法

刘健伶,陈志刚,王磊

(西安交通大学电子与信息工程学院, 710049, 西安)

针对广义空间调制(GSM)算法不能充分地利用信道状态信息的缺陷,提出了一种适用于GSM系统的自适应调制算法(AGSM),该算法利用已知信道状态信息,通过最大化空间调制星座点的最小欧氏距离,实现天线组合和符号调制星座的联合优化。进一步提出了一种低复杂度AGSM算法(LA-GSM),通过减少可选符号调制星座数量,并在传统天线组合集合与剩余天线组合集合中分别自适应选择相同符号调制星座,实现较低复杂度的天线组合和符号调制星座的联合优化,同时兼顾系统空间分集增益。仿真结果表明:在相同系统频谱效率5 b/(s·Hz)和6根发射天线条件下,所提的AGSM和LA-GSM算法以一定的算法复杂度为代价,均获得了相比于传统GSM算法更低的误码率性能,特别是在较高信噪比时AGSM算法和LA-GSM算法的误码率分别近似为GSM算法误码率的1/10和1/3;同时,LA-GSM算法获得了低误码率性能与低算法复杂度的较好折中。

自适应空间调制;信道状态信息;联合优化;天线组合

在无线通信技术中,由于空间调制(space modulation, SM)每次只激活一根发射天线,能够很好地解决MIMO系统中的信道间干扰(ICI)、天线间同步(IAS)以及较大的射频链路开销等问题,因而获得了广泛的研究[1-3]。

传统空间调制技术存在发射天线数必须为2的指数倍、频谱效率较低、没有发射分集增益等问题,针对这些问题,文献[4-5]进一步提出了广义空间调制(generalized space modulation, GSM)技术,GSM将每次激活的天线数由一根增加到多根,多根发射天线相互组合发送符号。相比于SM,GSM不限制总发射天线数,频谱效率有一定的增加;相比于MIMO,GSM不需要很多的射频链路,而且由于GSM同时隙激活的天线可以发送相同的符号也可发送不同的符号,因此能够很好地在频谱效率和性能之间进行折中,具有很高的灵活性。

目前,已有的空间调制技术大致可以分为开环空间调制技术和闭环空间调制技术。开环空间调制技术,如文献[1-5]中的SM和GSM不需要反馈链路,复杂度较低,但这类技术通常未能有效地利用信道状态信息。闭环空间调制技术则可以在接收端根据信道状态信息选择一组最优的发射天线子集[6-12],增加了系统的选择分集增益,有效地提高系统的误码率(BER)性能,或选择出最适合的发射天线并优化其对应的符号调制星座[6],即SM自适应调制方法,通常这类方法能够改善系统BER性能,但具有较高的复杂度。文献[7]进一步提出了基于有限反馈的ASM方法,通过筛选候选概率大的可能调制天线和符号星座组合,缩小候选集合中的候选天线及符号星座组合范围,从而降低优化复杂度和反馈开销,同时获得接近ASM方法的性能,但是已有的自适应空间调制技术主要适用于传统的SM系统。针对GSM系统,已有的自适应算法[13-14]根据信道状态优化选择符号星座或者天线组合,但未能充分地利用信道状态信息实现天线组合和符号星座的联合优化。

本文提出了一种针对广义空间调制系统的自适应算法(AGSM),该算法利用已知信道状态信息,通过最大化天线组合与符号调制星座对应的空间星座点的最小欧氏距离,实现天线组合和符号调制星座的联合优化,从而提升了系统的性能。进一步,针对AGSM复杂度高的缺点,本文提出了一种简化的自适应广义空间调制算法(LA-GSM),该算法通过减少可选符号调制星座数量,并在传统天线组合集合与剩余天线组合集合中分别自适应选择相同符号调制星座,实现较低复杂度的天线组合和符号调制星座的联合优化,同时兼顾系统空间分集增益。

1 广义空间调制系统模型

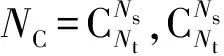
(1)

(2)

式中:y是Nr×1维的接收信号矢量;H是Nr×Nt维的瑞利衰落信道增益矩阵,其中的元素表示发射天线到接收天线之间的信道增益系数,是方差为1、均值为0的复高斯随机变量;x是Nt×1维的发射信号矢量;Es为发射信号的能量;n为Nr×1维的复高斯噪声矢量;m(p,i)表示第p个天线组合集合中的第i组天线组合采用的符号调制星座序号,SΘp(i,j)为第Θp(i,j)个天线发送的符号。于是,可以得到GSM系统的频谱效率为

(3)

2 AGSM算法及简化算法

2.1 AGSM算法

文献[6]已提出针对SM系统的自适应调制算法:SM系统接收端根据信道状态信息,在保证系统总的频谱效率一定的情况下,给不同的天线匹配不同的符号调制星座,使得系统的空间调制星座的最小欧氏距离达到最大,从而提高系统的BER性能。

SM系统中自适应调制算法为每一个激活的天线选择最优符号星座,即ASM算法只需要优化选择符号星座,而GSM系统中的天线组合数大于所需的组合数,其自适应广义空间调制(adaptive generalized spatial modulation, AGSM)算法需要针对天线组合与符号调制星座联合优化,选择一个天线组合集合Θp=[Θp(1),…,Θp(i),…,Θp(N)]T及其中各天线组合相应的符号调制星座Ωm(p,1),…,Ωm(p,i),…,Ωm(p,N),即选择一种空间调制星座Φ(p;m(p,1),…,m(p,i),…,m(p,N)),该空间调制星座具有最大的最小空间星座点欧氏距离,并将其反馈给发射端,发射端再进行相应的空间调制映射。

图1为当Ns=2时的AGSM算法原理图,接收端根据当前信道状态信息,实现激活天线序号检测和符号星座(APM)解调,并利用信道状态信息,优化选择天线组合集合及其中各天线组合相应的符号调制星座,并将优化选择结果反馈给发送端。在发送端根据反馈实现相应的天线组合集合和相应的符号调制星座选择。

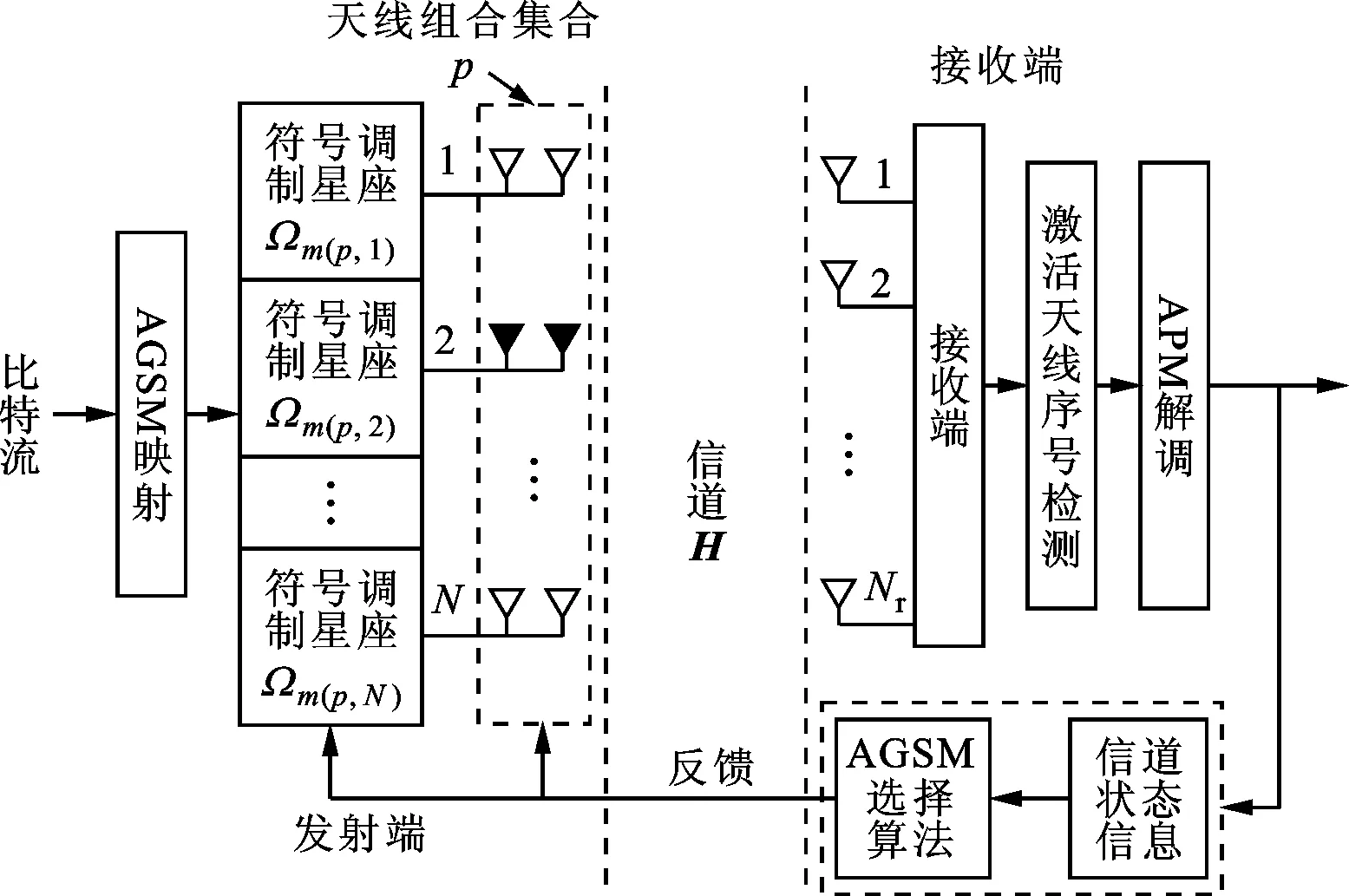
图1 Ns=2时AGSM算法原理图

与文献[6]类似,系统通过最大化最小空间星座点欧氏距离提高BER性能。令xk、xj为GSM系统空间调制星座Φ(p;Ωm(p,1),…,Ωm(p,i),…,Ωm(p,N))中的2个不同星座点,该空间调制星座的最小欧氏距离可以表示为

(4)

式中:H为Nr×Nt维的信道增益矩阵。

算法通过最大化空间调制星座的最小欧氏距离,选择最优的空间调制星座,即选择最优的一个天线组合集合及其对应的符号调制星座集合,AGSM算法表示为

(5)

式中:|Ωm(p,i)|为符号星座Ωm(p,i)对应的星座点数;ξ为给定的系统频谱效率。

通过式(5),系统遍历搜索所有可能的天线组合集合及其中各天线组合对应的符号调制星座,得到具有最大的最小欧氏距离的空间调制星座并反馈给发射端,发射端再按照所选空间调制星座发送符号。因此,AGSM算法不仅进行了天线组合集合选择,获得了天线选择增益,而且还进行了天线组合对应的自适应符号调制星座选择。

2.2 低复杂度的GSM自适应调制算法

由式(3)不难看出,AGSM算法具有很高的计算复杂度,同时存在部分剩余天线组合没有得到充分利用的缺点,为克服这些缺点,本文进一步提出了低复杂度的GSM自适应调制(low-complexity adaptive GSM, LA-GSM)算法。

(6)

(7)

(8)

式中:SΘp(i,j)和SΞp,q(i′,j′)分别表示第Θp(i,j)和Ξp,q(i′,j)个天线发送的符号;Ψ(p,Ωm(p),q,Ωm′(p,q))表示LA-GSM系统中空间调制星座,由2部分星座点集合构成,一是第p个可能天线组合集合Θp中所有天线组合均采用相同符号星座Ωm(p)所对应的可能激活天线组合和符号构成的星座点集合,二是第q个可能剩余天线组合集合Ξp,q中所有天线组合均采用相同符号星座Ωm′(p,q)所对应的可能激活天线组合和符号构成的星座点集合。

与AGSM算法类似,在式(8)给出LA-GSM空间调制星座的基础上,可以通过最大化空间调制星座点最小欧氏距离实现空间调制星座的优化选择,即LA-GSM的空间调制星座选择算法可以表示为

(9)

(10)

(11)

式中:xk、xj表示该空间调制星座的2个星座点,xk,xj∈Φ(p,Ωm(p),q,Ωm′(p,q))且xk≠xj;|Ωm(p)|和|Ωm′(p,q)|分别为符号星座Ωm(p)和Ωm′(p,q)对应的星座点数;ξ为给定的系统频谱效率。

LA-GSM算法遍历搜索所有可能的天线组合集合和剩余天线组合集合及其中天线组合对应的调制星座,且天线组合集合中的各天线组合和剩余天线组合集合中的各天线组合分别采用相同的符号星座,得到具有最大的最小欧氏距离的空间调制星座并反馈给发射端,发射端再按照所选空间调制星座发送符号。需要说明的是,在接收端检测方面,AGSM算法和LA-GSM算法均要求接收端先检测出天线组合的序号,再检测出发送的符号。

3 算法复杂度分析

选取典型参数如下:可选符号调制星座为{BPSK,QPSK,8PSK},激活发射天线数Ns=2和发射天线数分别为Nt=6和Nt=4,给定系统频谱效率分别为ξ=4 b/(s·Hz)和5 b/(s·Hz)。LA-GSM与AGSM算法复杂度如表1所示,从表1中可以看出,LA-GSM算法相比于AGSM算法的遍历复杂度要低一个数量级,且可以看出复杂度的降低主要是由于天线组合集合和剩余天线组合集合各自的天线组合分别采用了同样的符号星座,从而降低了符号调制星座组合数,减少了空间调制星座遍历范围。

表1 LA-GSM与AGSM算法的复杂度比较

4 仿真结果

为进一步验证算法性能,采用仿真实验比较本文所提算法和已有算法在相同频谱效率条件下的误码率性能。仿真中假定各天线之间的信道是相互独立的,并且服从复数正态分布。仿真中传统GSM系统采用典型配置参数Nt=6,Ns=2,频谱效率为5 b/(s·Hz),相同频谱效率下,按照空间调制自适应算法中系统频谱效率式(3)、式(5)和式(10),可得到本文所提算法AGSM和LAGSM的配置参数,如表2中所示。

根据表2中3种算法的仿真参数进行仿真,图2给出了AGSM、LA-GSM和GSM这3种算法的误比特率性能对比。

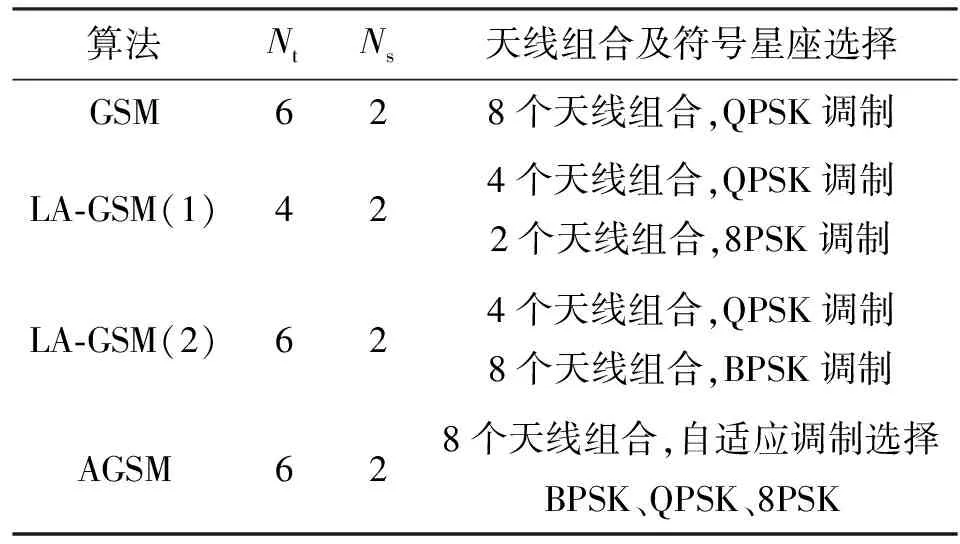
表2 几种空间调制算法的仿真参数

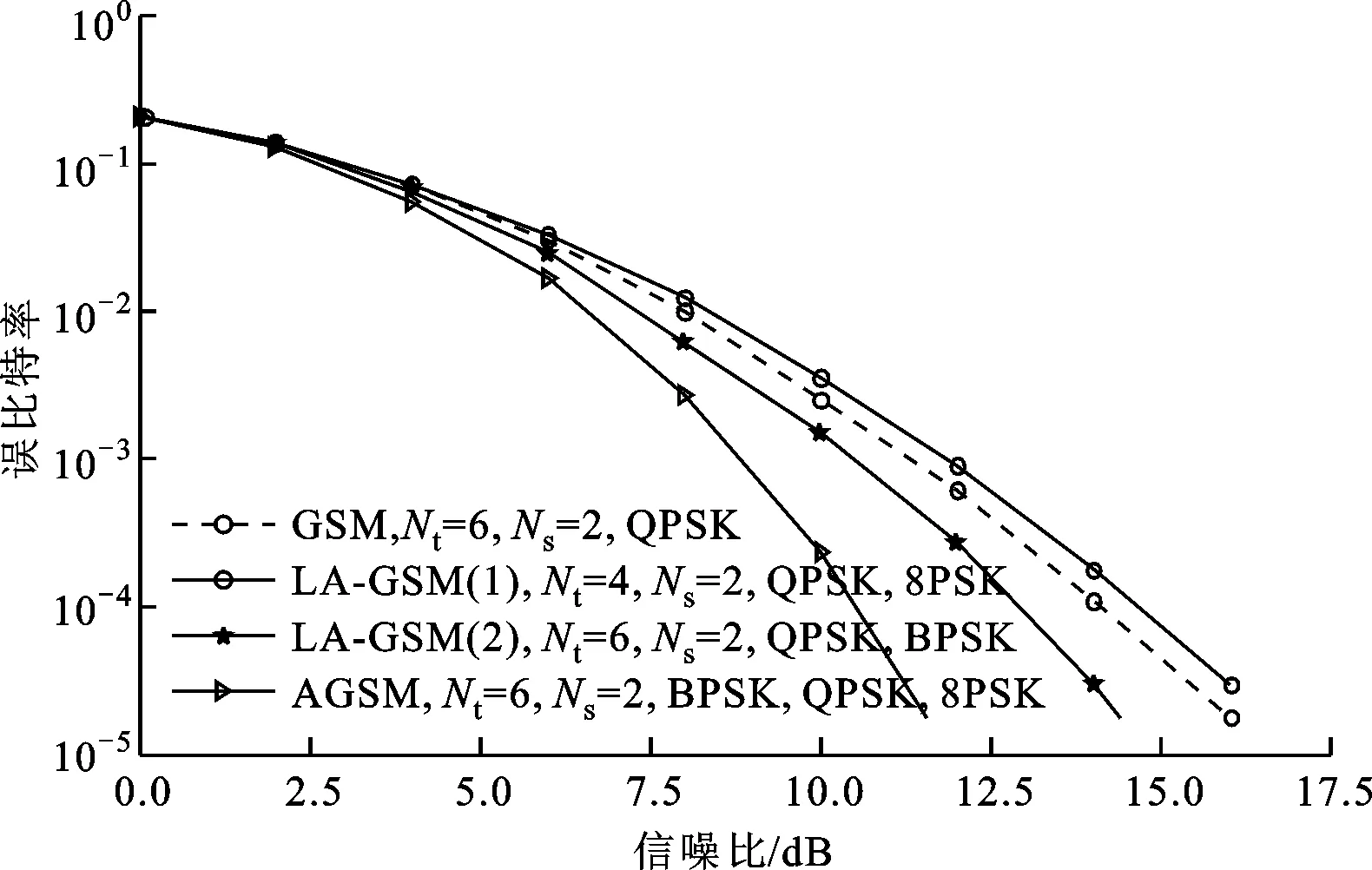
图2 AGSM、LA-GSM和GSM算法的BER性能对比

从图2中可以看出:在频谱效率均为5 b/(s·Hz)的条件下,AGSM、LA-GSM算法均获得了较GSM更好的性能,这是由于AGSM、LA-GSM算法均充分地利用了信道状态信息,获得了选择分集增益。

从图2中还可以看到:LA-GSM(1)算法在总天线数比GSM少2根的情况下,仍能够获得与GSM相近的性能,这是由于LA-GSM(1)算法采用自适应符号调制星座优化实现的;LA-GSM(2)算法在总天线数与GSM算法天线数相同的条件下,获得了比GSM和LA-GSM(1)算法更好的性能,这是因为天线组合数变多,LA-GSM(2)比GSM和LA-GSM(1)获得了更大天线选择增益。需要指出的是,由于AGSM遍历所有的天线组合集合与其中各天线组合分别采用可能的符号调制星座组合,而LA-GSM为获得较低计算复杂度只遍历所有天线组合集合与剩余天线组合集合及其中天线组合采用相同的可能符号星座组合,因此由图2还可以看出,当AGSM与GSM、LA-GSM天线总数相同时,性能为最优,且由前面分析可知其复杂度最高,而LA-GSM获得略差于AGSM的性能,同时获得了较低复杂度。综合仿真性能与复杂度分析,AGSM以高复杂度为代价,充分利用了信道状态信息且获得了选择分集增益,具有最好的性能,而LA-GSM算法能够在复杂度和选择分集增益之间获得更好的折中。

5 结 论

针对传统广义空间调制(GSM)算法不能充分地利用信道状态信息的缺陷,本文提出了一种GSM系统自适应调制算法,该算法利用已知信道状态信息,通过天线组合和符号调制星座的联合优化,使得系统的性能得到了有效地提升。进一步提出了一种简化的广义空间调制系统自适应调制算法LA-GSM,通过减少可选符号调制星座数量,并在传统天线组合集合与剩余天线组合集合中分别自适应选择相同符号调制星座,实现较低复杂度的天线组合和符号调制星座的联合优化,同时兼顾系统空间分集增益。仿真结果表明:所提的AGSM算法和LA-GSM算法以一定的算法复杂度为代价,均获得了相比于传统GSM较好的性能增益,且LA-GSM算法获得了系统性能与算法复杂度的较好折中。

[1] MESLEH R Y, HAAS H, SINANOVIC S, et al. Spatial modulation [J]. IEEE Transactions on Vehicular Technology, 2008, 57(4): 2228-2241.

[2] JEGANATHAN J, GHRAYEB A, SZCZECINSKI L. Spatial modulation: optimal detection and performance analysis [J]. IEEE Communications Letters, 2008, 12(8): 545-547.

[3] 陈诚, 王磊, 李晓峰. 采用星座旋转的高速率空时分组码空间调制算法 [J]. 西安交通大学学报, 2014, 48(12): 113-119. CHEN Cheng, WANG Lei, LI Xiaofeng. A high rate space-time block coding spatial modulation algorithm using constellation rotation [J]. Journal of Xi’an Jiaotong University, 2014, 48(12): 113-119.

[4] YOUNIS A, SERAFIMOVSKI N, MESLEH R, et al. Generalized spatial modulation [C]∥IEEE Conference Record of the Forty Fourth Asilomar Conference on Signals, Systems and Computers. Piscataway, NJ, USA: IEEE, 2010: 1498-1502.

[5] FU J, HOU C, XIANG W, et al. Generalized spatial modulation with multiple active transmit antennas [J]. IEEE Globecom Workshops, 2010, 29(16): 839-844.

[6] YANG P, XIAO Y, YU Y, et al. Adaptive spatial modulation for wireless MIMO transmission systems [J]. IEEE Communications Letters, 2011, 15(6): 602-604.

[7] YANG P, XIAO Y, YU Y, et al. Simplified adaptive spatial modulation for limited-feedback MIMO systems [J]. IEEE Transactions on Vehicular Technology, 2013, 62(6): 2656-2666.

[8] RAJASHEKAR R, HARI K V S, HANZO L. Antenna Selection in spatial modulation systems [J]. IEEE Communications Letters, 2013, 17(3): 521-524.

[9] PILLAY N, XU H. Comments on antenna selection in spatial modulation systems [J]. IEEE Communications Letters, 2013, 17(9): 1681-1683.

[10]NTONTIN K, DI RENZO M, PEREZ-NEIRA A I, et al. A low-complexity method for antenna selection in spatial modulation systems [J]. IEEE Communications Letters, 2013, 17(12): 2312-2315.

[11]龚丽莎, 尹露, 龚赛丹, 等. 基于空间调制的天线选择和能效优化算法 [J]. 电子科技大学学报, 2014, 43(4): 497-501. GONG Li-sha, YIN Lu, GONG Sai-dan, et al. Transmit antenna selection and energy efficiency improvement for spatial modulation [J]. Journal of University of Electronic Science and Technology of China, 2014, 43(4): 497-501.

[12]ZHENG J, CHEN J. Further complexity reduction for antenna selection in spatial modulation systems [J]. IEEE Communications Letters, 2015, 19(6): 937-940.

[13]WANG Wen-Hsin, CHANG R Y. Signal-spatial constellation optimization for generalized spatial modulation [C]∥IEEE 79th Vehicular Technology Conference. Piscataway, NJ, USA: IEEE, 2014: 1-5.

[14]NING M, ANGUO W, CHANGCAI H, et al. Adaptive Joint Mapping Generalised Spatial Modulation [C]∥IEEE International Conference on Communications in China. Piscataway, NJ, USA: IEEE, 2012: 520-523.

(编辑 刘杨)

An Adaptive Modulation Algorithm with Low Complexity for Generalized Spatial Modulation

LIU Jianling,CHEN Zhigang,WANG Lei

(School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A new adaptive modulation algorithm for generalized spatial modulation (AGSM) is proposed to make full use of the channel state information. The algorithm realizes the joint optimization of antenna combinations and symbol modulation constellations by using the known channel state information and maximizing the minimum Euclidean distance of space-modulation constellation points so that the system performance is improved. Furthermore, a low-complexity AGSM algorithm (LA-GSM) is proposed to reduce the complexity of the joint optimization of antenna combinations and symbol modulation orders. The LA-GSM achieves a lower complexity and makes full use of the antenna combinations of GSM systems by reducing the number of available symbol modulation constellations and searching the identical symbol modulation constellations from the typical antenna combinations and remanent antenna combinations adaptively and respectively. Simulation results show that both the AGSM and the LA-GSM achieve much lower BER performance than the GSM does at a cost of certain complexity under same system spectral efficiency 5 b/(s·Hz) and 6 transmit antennas. Especially, the AGSM’s BER and LA-GSM’s BER are 1/10 and 1/3 of GSM’s one, respectively, when the SNR is high. Moreover, the LA-GSM achieves a better trade-off between lower BER performance and lower complexity.

adaptive spatial modulation; channel state information; joint optimization; antenna combinations

2015-08-09。 作者简介:刘健伶(1989—),男,硕士生;陈志刚(通信作者),男,讲师,硕士生导师。 基金项目:陕西省自然科学基金资助项目(2015JM6305);华为创新研究计划资助项目(YB2015070059).

时间:2016-02-25

10.7652/xjtuxb201604008

TN911.7

A

0253-987X(2016)04-0048-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160225.1555.010.html