爆破阀可靠性试验数据处理方法研究
吴 杰, 何 劼, 包堂堂
(上海核工程研究设计院, 上海 200233)
爆破阀可靠性试验数据处理方法研究
吴 杰, 何 劼, 包堂堂
(上海核工程研究设计院, 上海 200233)
将核电厂爆破阀三部分(点火器、药筒、机械组件)可靠性试验的数据分别转化为Beta分布,并通过蒙卡抽样方法,求解爆破阀的可靠度先验分布,结合数据质量因子的贝叶斯更新方法和整机试验数据得到爆破阀的可靠性后验分布。
爆破阀; 可靠性数据; Beta分布; 蒙卡抽样
爆破阀作为AP1000和CAP1400中的关键设备[1-2],其可靠性一直受到业内的关注。为了判断爆破阀的可靠性是否达到要求,需要进行一定样本量的可靠性验证试验。根据爆破阀的可靠度指标要求,若通过计数法来验证系统的可靠度指标,在置信度γ=0.95,可靠度为0.999,需要进行2994次系统试验且无一失效,如果出现失败,应进行更多的系统试验。更何况一个爆破阀的制造成本接近百万,显然采用这种方法不可行。笔者将爆破阀分成三部分(点火器、药筒、机械组件)分别进行可靠性试验,将每部分的可靠性数据整合成爆破阀整机的可靠性分布,并结合整机试验样本采用数据质量因子的贝叶斯更新方法,最终得到爆破阀的可靠度。该方法能够充分利用可靠性试验的数据,引入的偏差较少,适用于爆破阀可靠性试验中的数据处理。
1 爆破阀分析思路
利用PSA故障树分析方法,将爆破阀分成三部分(点火器、药筒、机械组件)进行研究分析。
爆破阀的故障树见图1,将爆破阀失效看成是顶事件,点火器瞎火、药筒失效和机械组件失效是导致爆破阀不能开启的基本事件。
点火器部分、药筒失效(传爆失效)的可靠性评估[3]可以利用火工品方面比较成熟方法进行可靠性评估,机械组件可靠性分析可以采用可靠性试验与力学理论分析相结合等方法进行研究。在各部分用相对成熟的可靠性评估方法,可以大幅减少试验次数,从而大大降低试验成本。
笔者主要研究的是如何将三部分可靠性试验得到的可靠性数据处理得到爆破阀的整体可靠性分布,其主要流程见图2。
2 可靠性试验数据转化为Beta分布
观察爆破阀故障树,三部分是或门关系,只有三部分都成功,爆破阀才算成功开启。假定爆破阀的可靠度为R0,点火器的可靠度为R1,药筒的可靠度为R2,机械组件的可靠度为R3。三部分的可靠性分析结果是以置信度γ下的可靠度下限RL给出的。三部分都是伯努利过程,每次试验只有“成功”和“失败”两个结果,所以N个试验的成功次数是服从二项分布的。对于计数试验,在进行N次试验,知道成功次数S和失效次数F,就能算出某置信度下的可靠度下限值[4]。相应的,在通过可靠性试验得到可靠度下限值的基础上,可以合理地假设为是通过N次成败型计数试验的结果计算得出的,从而将可靠性数据转化为计数试验的样本量,如点火器的可靠度下限达到了0.999,当置信度为0.95时,转化为计数试验的样本量,当全成功时,样本量为2994,即相当于进行了2994发试验,全发火,0次失效。
Beta分布的概率密度函数[5]为:
(1)
Beta分布的概率分布函数为:
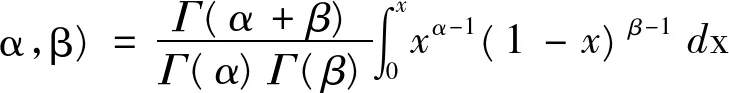
(2)
当α、β为正整数时,对上述积分项进行分部积分得[6]:
(3)
得:

F(x|α+1,β-1)
(4)
对F(x|α+1,β-1)进行再一次分部积分,依此类推,最后得:

(5)
很显然,式子左边是Beta分布的概率分布函数,式子右边是二项分布的概率分布函数。因此在α、β为正整数时,存在上述等式(5)。假定x为成功概率,若进行N次试验,失效次数为F,成功次数为S,则在置信度γ下,可靠度下限RL满足:
(6)
通过上式可转化为:
F(RL|S, F+1)=1-γ
(7)

观察公式(7),F(RL|S, F+1)是Beta分布的概率分布函数,其中S作为参数不能等于0,即成功次数不能等于0,但是现实情况是存在的,存在矛盾。求的是RL,当S等于0时,即N次试验N次失效,置信度为γ可靠度下限RL的含义是有γ的概率(把握)可靠度的值是高于RL的,当N次试验N次失效,从直接计算可靠度的算数平均值为0,此时可靠度是不存在下限值的,因为从样本信息(N次试验,全部失效)上看,没有把握认为可靠度值会高于某个非0正数。但是此时其实是存在可靠度的上限值RU的,即有γ的概率(把握)可靠度的值是低于RU的。
因此得出结论,对于N次试验,F次失效,S(S≠0)次成功的成败型试验,其置信度为γ可靠度下限RL值是B(S, F+1)的(1-γ)分位点值。
对于爆破阀的三部分,其可靠性是分别以置信度γ下可靠度下限RL给出的,将可靠性数据转化为N次成败型试验。通过式(5)的推导,可靠度R满足B(S, F+1)分布。
3 蒙卡抽样拟合可靠度分布
爆破阀的故障树中,三部分是或门关系,可靠度表示为:
R0=R1×R2×R3
(8)
当R1、R2、R3为定值时,很容易算出爆破阀可靠度R0,然而R1、R2、R3服从对应的Beta分布,分布参数间相互独立,因此难以进行数学上严格求解R0的概率密度函数。可以利用蒙卡方法(统计模拟方法),利用随机数来解决复杂的计算问题。
文献[7-8]提到,两个Beta分布的乘积近似为Beta分布。特殊的对于B(a1,b1),B(a2,b2),当a2=a1+b1时,通过公式推导可得,两者乘积服从B(a1,b1+b2);由对称性可得,a1=a2+b2时,两者乘积服从B(a2,b1+b2)。对于其他情况,难以给出精确的数学表达。很显然,对于三个Beta分布相乘,其结果近似为Beta分布。笔者采用矩法估计的方法,令一阶矩、二阶矩(方差)相等求解Beta分布的参数。Beta分布与蒙卡抽样的拟合程度,可以通过拟合优度检验的方式判断。
假设H0为f(x)=f0(x),H1为f(x)≠f0(x),其中:
(9)
由皮尔逊分布拟合检验方法可知,皮尔逊统计量η为:
(10)式中:m为分组数;ki为样本出现的个数;npi为理论上出现的个数(由分布算出)。η服从以自由度为m-1的χ2分布。显著性水平θ下,其拒绝域为:
(11)
对于爆破阀试验求得的三部分的可靠性参数,分三种情况进行讨论分析:
(1) 三部分可靠度相近。假设给出的可靠度为在95%置信度下分别为0.9996、0.9997、0.9995;三部分可靠度很接近,并且可靠度都很高,可转化为等效的零失效成败型计数试验,计算得:7488、9984、5990。因此三部分的可靠度分别满足Beta分布:B(7488,1)、B(9984,1)、B(5990,1)。根据蒙卡方法抽样100万个样本点,令样本与模拟的Beta分布一阶矩与二阶矩分别相等,求出爆破阀可靠度R服从B(7205.1,2.8874)。

因此在爆破阀三部分可靠度较接近的情况下,可以采用拟合的Beta分布作为爆破阀的可靠度的分布。
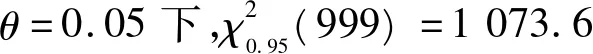
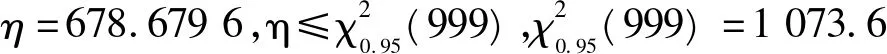
对于上述三种情况的分类讨论,可以得出结论:矩法估计得到的Beta分布与蒙卡抽样的结果拟合较好,引入的误差很小,因此可以把该Beta分布作为所研究的爆破阀可靠度的先验估计。
4 数据质量因子的贝叶斯更新
为了使可靠性分析的结论更有说服力,需要进行一定的整机试验,将爆破阀整机试验的样本与求得的爆破阀可靠度拟合分布进行贝叶斯更新作为爆破阀的可靠度估计。爆破阀整机试验花费较大,难以做大样本试验,考虑到样本较小时,先验信息会淹没样本信息的情况,引入数据质量因子修正贝叶斯公式。
在小子样的贝叶斯更新中,先验信息会淹没试验样本,从而导致后验分布对于先验信息的依赖很大。文献[9-10]引入先验数据质量因子p和整机试验信息质量因子q来描述对获取数据的信任程度。后验分布满足:π(R|X)=π(R)pL(X)q,p、q∈[0,1],π(R)为先验分布,L(X)为整机试验数据,推导得到R的后验分布为:
π(R|(S,F))=B((α-1)p+Sq+1,
(β-1)p+Fq+1)
(12)
当p=0、q=1时,认为先验数据质量极差,此时退化为无先验信息的经典统计方法;当p=1、q=0时,认为先验数据是可信的,而现场试验信息质量极差;当p=1、q=1时,认为先验信息和现场试验数据都可信,退化为一般的贝叶斯更新方法。数据质量因子可以由试验信息结合专家经验来确定,也可以利用分层贝叶斯方法的思想确定合适的概率分布来描述数据质量因子的不确定性,以增加可靠性评估的稳健性。从本质上看,这种方法是利用数据质量因子对先验信息和现场试验信息进行加权融合。
5 模拟计算与运用
5.1模拟计算
根据现阶段的初步研究和以往爆破阀运行经验,火工品部分(点火和药筒)相对于机械组件的部分其可靠性相对较差,因此假定:爆破阀点火器、药筒和机械组件的95%置信度下的可靠度下限值为0.9995、0.9996、0.99993;目前预算内爆破阀的可试验次数约为13次。
分析可靠度,0.9995与0.9996相近但比0.99993低一个量级左右,因此将0.9995转化为1次失效的等效计数试验,0.9996转化为1次失效的等效计数试验,0.99993转化为0次失效的等效计数试验。从而计算得到:点火器服从B(9485,2)分布,药筒服从B(11857,2)分布,机械组件服从B(42795,1)分布。
进行蒙卡抽样,利用矩法估计求得蒙卡抽样拟合分布为B(10975,4.3735)。
假定爆破阀试验为13次试验,0次失效,认为实验数据可信,认为先验信息部分可信,取Bp=0.8,q=1,则后验分布为:B(8713.2,3.6988)。
求得后验的95%置信度的可靠度下限值RL为0.999160。
5.2反向推演指导可靠性试验
爆破阀是风险重要的设备,其可靠性数据一直是关注的重点,进行爆破阀可靠性评估的目的也是要论证其可靠性。NUREG/CR-6928[11]中爆破阀失效率的通用数据是10-3,目前PSA分析中也是使用这一通用数据,这给了可靠性评估的目标参考,因此设定可靠性评估的目标是95%置信度下爆破阀的可靠度下限为0.999;通过分析研究爆破阀三部分之间的可靠性分配关系,就可以计算得到每一部分所应该达到的可靠性指标,从而给每一部分的可靠性试验给出一个可靠度下限的参考值,为制定较为合适的可靠性试验方案提供参考。
6 结语
笔者采纳的方法能够将分步骤的爆破阀可靠性试验的数据进行有效利用,选取了合适的可靠性模型,作了适当假设,得到拟合的Beta分布与蒙卡抽样拟合较好,引入的偏差较少,并考虑了保守性,引入了数据质量因子的贝叶斯方法求解爆破阀的后验分布。因此该方法适用于爆破阀的可靠性数据处理,并且可推广到成败型设备的可靠性试验数据的整合处理。
[1] 熊冬庆, 王闯, 邓冬. AP1000爆破阀研制进展与技术难点分析[C]//2014年核电站新技术交流研讨会论文集. 青岛: 中国电机工程学会核能发电分会, 2014.
[2] 耿绪超. 浅析爆破阀在AP1000核电厂中的应用[J]. 中国机械, 2015(9): 107-108.
[3] 王金武, 张兆国. 可靠性工程基础[M]. 北京: 科学出版社, 2013.
[4] 国防科学技术工业委员会. 火工品可靠性评估方法: GJB 376—1987[S]. 北京: 国防科学技术工业委员会, 1987.
[5] 茆诗松, 程依明, 濮晓龙. 概率论与数理统计教程[M]. 2版. 北京: 高等教育出版社, 2012.
[6] 方开泰, 许建伦. 统计分布[M]. 北京: 科学出版社, 1987.
[7] 王小平, 魏振军. 用数值方法及计算机模拟寻求两个贝塔分布r·v乘积的分布[J]. 信息工程大学学报, 2003, 4(1): 82-85.
[8] 陈伟志, 米顺强, 魏振军. 一种判定两个随机变量的乘积(和)服从何种分布的方法[C]//中国现场统计研究会2003年学术年会论文集. 郑州: 中国现场统计研究会, 2003: 23-27.
[9] 张士峰, 杨华波, 张金槐. 小样本成败型设备可靠性评估方法[J]. 核动力工程, 2006, 27(5): 79-83.
[10] 杨华波, 张士峰, 蔡洪. 成败型产品可靠性评估的Bayes修正幂验前方法[J]. 固体火箭技术, 2009, 32(2): 131-134, 149.
[11] U.S. Nuclear Regulatory Commission. Industry-average performance for components and initiating events at U.S. commercial nuclear power plants:NUREG/CR-6928[S]. Washington,DC:U.S. Nuclear Regulatory Commission, 2007.
Research on Data Processing Method in Reliability Experiment of Squib Valve
Wu Jie, He Jie, Bao Tangtang
(Shanghai Nuclear Engineering Research & Design Institute, Shanghai 200233, China)
The data of reliability experiment for three parts (igniter, cartridge case and mechanical component) of squib valve were respectively converted into Beta distribution, so as to work out the reliability prior distribution by Monte Carlo simulation, and then to obtain the posterior distribution by Bayesian updating method within quality factors of prior and sample data.
squib valve; reliability data; Beta distribution; Monte Carlo simulation
2016-03-11
吴 杰(1990—),男,在读硕士研究生,研究方向为概率安全分析。
E-mail: wujie@snerdi.com.cn
TM623
A
1671-086X(2016)06-0412-05

