基于分子信标的可满足性问题的粘贴模型
陈玉华 殷志祥
摘要:为了解决NP完全问题中的可满足性问题,将分子信标和粘贴模型的优势结合起来,设计了一种新的以分子信标为粘贴链的粘贴模型,并将该模型应用于可满足性问题的求解。由于分子信标具有易操作、高灵敏度、高特异性等特点,将分子信标作为粘贴链,分子信标粘贴链比普通粘贴链链更有优势,利用该模型求解问题的操作简单且容易观测,求得问题的解比普通的粘贴模型更准确可靠。
关键词:分子信标;粘贴模型;可满足性问题
中图分类号:TP301文献标志码:A
文章编号:1672-1098(2016)02-0020-05
Abstract:In order to solve the problem of NP complete problem, by combining the advantages of molecular beacon and sticker model, a new method of molecular beacon was designed, which is used to solve the satisfiability problem. Because of the characteristics of easy operation, high sensitivity, high specificity, etc., molecular beacon is used as a sticker chain, the molecular beacon sticker chain is more advantageous than the ordinary sticker chain. The operation of solving the problem by using the model is simple and easy to observe, and the solution is more accurate and reliable than the ordinary sticker model.
Key words: molecular beacon; sticker model; satisfiability problem
DNA计算是一种新型的计算模式,它在解决NP完全问题上,所表现出来的优势是传统图灵机无法比拟的。正因如此,人们对DNA计算产生了浓厚的兴趣。1994年,美国加利福尼亚大学的博士Adleman开创了DNA计算领域,利用DNA分子成功解决了有向Hamilton路问题[1],为人们进一步研究DNA计算做好了铺垫,燃起了人们对解决NP完全问题的希望。在这之后的二十年里,DNA计算的研究取得了很大的成就。许多学者提出了不同的DNA计算模型,主要包括:粘贴DNA计算模型,插入-删除系统模型,自组装模型等,并将这些模型应用在求解NP完全问题上。对于粘贴模型,学者们利用该模型解决了不少NP完全问题,如图的最小覆盖问题、最大团问题、图的顶点着色问题[2-7]629等等。本文在前人研究粘贴模型的基础上,提出了一种新型粘贴模型,该模型不同于普通的粘贴模型,它是与分子信标相结合的一种新模型。由于分子信标具有易操作、高灵敏度、高特异性等特点,将分子信标融入粘贴模型,以分子信标作为粘贴链,这样的模型操作简单,比普通粘贴模型更易观测,结果更准确可靠。之后,本文将该模型应用于求解可满足性问题。可满足性问题是NP完全问题的经典问题之一,不少其它的NP完全问题都可以转化为可满足性问题来求解,所以可满足性问题非常具有代表性。
1分子信标
分子信标是一种茎环结构的寡聚核苷酸探针,分子信标由三个部分组成:环状区、茎干区、荧光基团和猝灭基团。环状区是分子信标的基团识别区,它的碱基序列是与靶基团互补的,碱基数一般为15~30个,能与靶基团进行特异结合;茎干区是由两列互补的碱基序列构成的,碱基对一般为5~8个,它的两个末端分别连接荧光基团和猝灭基团。在没有杂交反应的情况下,分子信标呈茎环结构,荧光基团与猝灭基团距离接近,猝灭基团猝灭了荧光基团发出的荧光,检测不到荧光信号。当发生杂交反应时,分子信标的环状区会与靶基团进行特异性结合,分子信标的结构被破坏,荧光基团与猝灭基团的距离被拉大,荧光基团因不能被猝灭基团猝灭而发出荧光,从而能检测到荧光信号(见图1)。
2粘贴模型
粘贴模型是由文献[2]622最早提出的,它在当前DNA计算模型中颇受学者们的关注。粘贴模型的优点在于在生物操作过程中既不需要酶的参与,也不需要DNA链的延长,并且它的材料可以循环利用。粘贴模型的重要特征在于有一个随机存取的存储区,在存取区中,存放了一系列的存取复合物。每个存取复合物都是由两类单链的DNA分子组成的,分别是存储链和粘贴链。一个存储链是由n个不重叠的子链组成的,而每个子链是由m个碱基组成的,从而可得存储链的长度l=m×n。粘贴链是与存储链中的一个子链互补的链,显然它的长度为m,粘贴链的数量小于或等于存储链中子链的数量。存储链中的每个子链代表一个二进制变量,只有两种取值可能:0或1。如果一个粘贴链与存储链中的一个互补子链发生退火反应,那么存储复合物对应的位元是开的,取值为1,否则,它是关闭的,取值为0。例如,存储复合物含有一个存储链和两个粘贴链,存储链含有4个子链,每个子链含有5个碱基。两个粘贴链分别与位1、位4的存储子链互补,则存储复合物的二进制表示是1001。
粘贴模型具有四个基本操作:
1)合并。此操作将两个含有存储复合物的试管T1和T2合并成试管T。
2)分离。此操作根据位元的取值,将试管T分成两个试管T1和T2。第i位取值为1的存储复合物存放于试管T1,第i位取值为0的存储复合物存放于试管T2。
3)设置。此操作将试管中所有第i位取值为0的存储复合物设置为1。
4)消除。此操作将试管中所有第i位取值为1的存储复合物设置为0。
3基于分子信标的粘贴模型
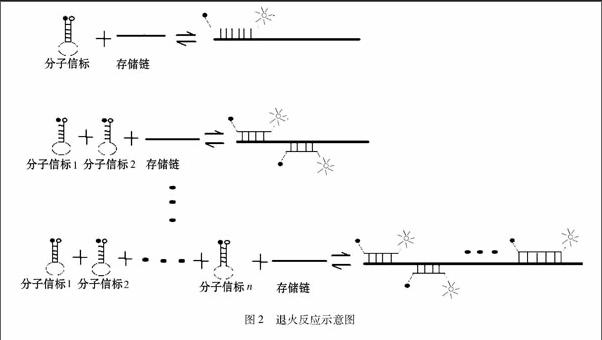
基于分子信标的粘贴模型跟普通的粘贴模型的构造相似,它的区别在于粘贴链不是普通存储链的子链的补链,而是用分子信标作为粘贴链。由于分子信标的环状区的编码是与靶基团互补的,该模型的粘贴链设计的分子信标环状区的编码是与存储链对应的子链互补的。因为分子信标环部识别区的碱基个数一般为15~30个,所以分子信标作为粘贴链时的环部识别区的碱基数应该不低于15个 例如,存储链是5′-ATCGATTACCGATATATCGATTACGTTAAC-3′,则分子信标粘贴链的环部识别区分别为3′-TAGCTAATGGCTATA和3′-TAGCTAATGCAATTG-5′。当分子信标与存储链上对应的子链发生退火反应时,分子信标的环状区与存储链上对应的子链结合,发夹打开,发出荧光。分子信标粘贴链与存储链上对应的子链发生退火反应如图2所示。
4可满足性问题的DNA计算
4.1可满足性问题
可满足性问题可表述为:由若干个析取范式合取构成的范式叫做合取范式,如F=C1∧C2∧…∧Cm,其中Ci(i=1,2,…,m)是形如l1∨l2∨…∨ln的析取式;由若干个合取范式析取构成的范式叫做析取范式,如F=C1∧C2∧…∧Cm,其中Ci(i=1,2,…,m)是形如l1∨l2∨…∨ln的合取式。li(i=1,2,…,n)表示ai或a′i,ai和a′i互为否定,它们的取值或是0或是1,“0”表示真值为真,“1”表示真值为假。可满足性问题是指对于给定的一个含有个变量的合取范式或者析取范式,是否存在一组或多组变量的取值使得该范式的真值为1。如果Ci(i=1,2,…,m)中的变量个数都小于或等于个,那么称其为-可满足性问题。
4.2 可满足性问题的DNA算法步骤
1)对给定的一个含有n变量的合取范式进行编码。先合成2n种短的寡聚核苷酸,把这2n种寡聚核苷酸分成两组,第一组的n种寡聚核苷酸分别表示变量x1,x2,…,xn,第二组的n种寡聚核苷酸分别表示为x1′,x2′,…,xn′,为了避免这两组寡聚核苷酸之间的不正确杂交,这两组的寡聚核苷酸应具有较大差异,保证它们起码要有四个以上是不同的。然后合成这两组寡聚核苷酸的补链,第一组的n种寡聚核苷酸的补链分别表示为x1,x2,…,xn,第二组的n种寡聚核苷酸的补链分别表示为x1′,x2′,…,xn′。
2)构造出的前2n种寡聚核苷酸有2n个不同的组合,而且每个组合都含有n个寡聚核苷酸对应的变量,利用杂交的方法将它们连接成2n个不同的DNA单链。则初始数据库T0共有2n个存储链。存储链的子链有n个,每个子链的长度与分子信标的环部识别区的长度相等,分子信标的环部是由15~30个碱基构成,取分子信标的长度为15,则每个子链是由长度为15的碱基序列构成。粘贴链是前两组的2n种寡聚核苷酸的补链,则粘贴链有2n个,而且这些粘贴链是特殊的链,它们是由分子信标构成的,分子信标的环部识别区与存储链中对应的子链互补。
存储链5′-ATCGATTACCGATATATCGATTACGTTAAC-3′,则分子信标粘贴链的环部识别区分别为3′-TAGCTAATGGCTATA和3′-TAGCTAATGCAATTG-5′。
3)对于范式中给定的一个子句,字句中含有变量xi或x′i,则往初始数据池T0加入对应的分子信标粘贴链xi或xi′,分子信标链的环部识别区与存储链上的变量xi或xi′进行退火反应,茎环结构被破坏,形成双链,并发出荧光。利用激光共聚焦显微镜观察存储链上的荧光情况。有荧光的存储链说明满足子句真值为真的条件,无荧光的存储链说明不满足子句真值为真的条件,记录下有荧光的存储链。
4)对第三步的产物进行加热解链,解开与存储链杂交的分子信标粘贴链,并将它们冲洗掉。
5)重复第三、四步,直到把给定范式的所有子句都检查完为止,删除范式中不满足真值为真的条件的子句,最后通过测序可以读出问题的解。
4.3 实例分析
取标准合取范式F=(x1∨x2)∧(x′1∨x′3)∧(x2∨x′3),算法步骤如下:
1)合成6种短的寡聚核苷酸,将这6种寡聚核苷酸分成两组,第一组的3种寡聚核苷酸分别表示为x1,x2,x3,第二组的3种寡聚核苷酸分别表示为x1′,x2′,x3′,然后合成这两组寡聚核苷酸的补链,它们分别为x1,x2,x3和x1′,x2′,x3′。
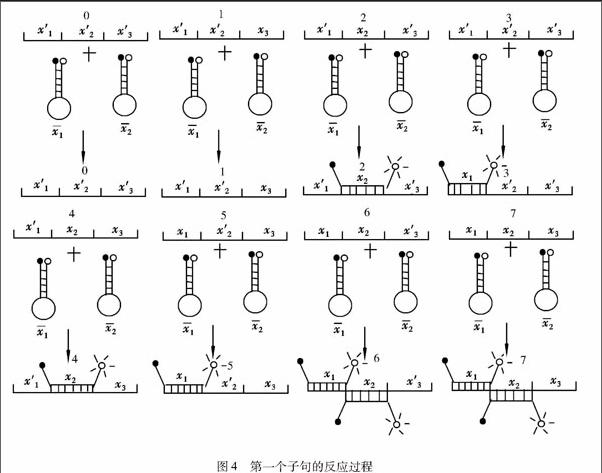
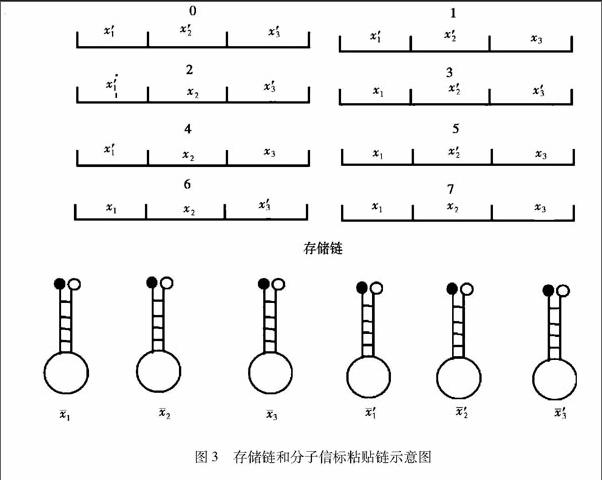
2)构造出的前6种寡聚核苷酸有8个不同的组合,而且每个组合都含有3个寡聚核苷酸对应的变量,利用杂交的方法将它们连接成8个不同的DNA单链。则初始数据库T0共有8个存储链。存储链的子链有3个,每个子链的长度与分子信标的环部识别区的长度相等,分子信标的环部是由15~30个碱基构成,取分子信标的长度为15,则每个子链是由长度为15的碱基序列构成。粘贴链是前两组的6种寡聚核苷酸的补链,则粘贴链有6个,而且这些粘贴链是特殊的链,它们是由分子信标构成的,分子信标的环部识别区与存储链中对应的子链互补,这6种分子信标粘贴链的茎干末端分别连接不同颜色的荧光基团(见图3)。
3)对于第一个子句x1Vx2,则往初始数据池T0加入对应的分子信标粘贴链x1和x2,分子信标链的环部识别区与存储链上的变量x1和x2进行退火反应,茎环结构被破坏,形成双链,并发出荧光。利用激光共聚焦显微镜观察存储链上的荧光情况。可以看出,满足第一个子句x1∨x2的真值为真的条件的存储链编号有2,3,4,5,6,7,并记录下来(见图4)。
4)重复第三步骤,则满足第二个子句x′1∨x3的真值为真的条件的存储链编号有0,1,2,4,5,7,满足第三个子句x2∨x3的真值为真的条件的存储链编号有1,2,4,5,6,7。删除范式中不满足真值为真的条件的子句后,最后通过测序可以读出问题的解,即(0,1,1),(1,0,1),(1,1,0)和(1,1,1)。
5结论
将分子信标技术融入粘贴模型,建立一种新的模型,即以分子信标作为粘贴链的粘贴模型,并将这种模型应用于可满足性问题的求解。在利用该模型求解问题的过程中,对于分子信标的粘贴链要求比较高,对DNA编码的设计比较重要,分子信标的环部识别区的编码要与存储链上对应的子链互补。该模型操作简单,且比普通的粘贴模型更容易观察和检测问题的解,从而得到更准确可靠的解。
参考文献:
[1]ADLEMAN L M.Molecular computation of solutions to combinatorial problems[J].Science, 1994, 266(5 187):1 021-1 023.
[2]ROWEIS S,WINFREE E,BURGOYNE R,et al.A sticker based architecture for DNA computation[J].Journal of Computational Biology, 1998, 5(4):615-629.
[3]RARI L,THIERRIN G.Contextual insertions deletions and computability[J].Information and Computation, 1996, 131(1):47-61.
[4]WINFREE E,LIU F,WENZLER L A,et al.Design and selfassembly of two-dimensional DNA crystals[J].Nature, 1998, 394(6):539-544.
[5]GAO L,MA RN,XU J.DNA solution of vertex cover problem based on sticker model[J].Chinese Journal of Electronics, 2002, 11(2):280-284.

