一种基于MPS和ISOMAP的空间数据重建方法

杜 奕 张 挺 黄 涛

1(上海第二工业大学工学部 上海 201209)2(上海电力学院计算机科学与技术学院 上海 200090)3(中国科学技术大学近代力学系 合肥 230027)(duyi@sspu.edu.cn)



一种基于MPS和ISOMAP的空间数据重建方法

杜 奕1张 挺2黄 涛3

1(上海第二工业大学工学部 上海 201209)2(上海电力学院计算机科学与技术学院 上海 200090)3(中国科学技术大学近代力学系 合肥 230027)(duyi@sspu.edu.cn)

在空间数据重建过程中,条件数据对重建结果影响较大，在仅有少量条件数据的情况下,重建结果常常出现较多的不确定性,此时适合采用不确定性插值方法重建空间数据.作为目前不确定性插值的主流方法之一,多点信息统计法(multiple-point statistics, MPS)可以从训练图像提取模式的本质特征,然后将这些特征复制到待模拟区域.由于传统采用线性降维的MPS方法无法有效处理非线性数据,因此将等距特征映射(isometric mapping, ISOMAP)应用到MPS方法,以实现对非线性数据的降维.提出基于MPS和ISOMAP的空间数据重建方法,通过模式库构建、模式降维、模式分类、模式提取等步骤能够较为准确地重构出未知的空间数据,为MPS处理非线性空间数据提供了新思路.实验结果表明:该方法所重建的空间数据具有与训练图像相似的结构特征.

训练图像;多点信息统计法;模式;等距特征映射;降维

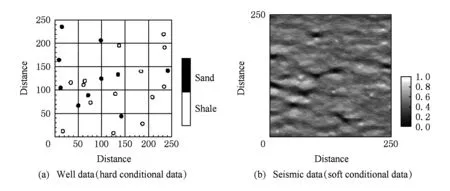
Fig. 1 Well data(hard conditional data) and seismic data(soft conditional data).图1 井位数据(硬条件数据)和地震数据(软条件数据)

空间数据是指包含空间特征的数据集合.现实生活中的空间数据,既有来自科学试验的数据,也有来自生产实践的数据,其格式与特征是包罗万象[1-3].与一般数据相比,空间数据具有一定的特点,主要表现在2个方面：1)空间数据除包含属性信息外,还含有空间信息；2)空间数据具有空间自相关性,即邻近数据间的相关性比距离较远的数据间的相关性要大得多[4-6].目前获取某些领域真实有效的空间数据存在一定的难度,出现这种情况的主要原因是科学实验难度大或勘探开发费用高.

数据插值成为重建空间数据的1个有效手段[7-8].插值方法可分为“确定”性插值方法和“不确定”性插值方法.“确定”性插值方法的插值形式、插值函数参数以及插值结果基本都是确定的[9-10].不确定性插值方法的不确定性一方面表现在选用的插值方式具有随机性,另一方面表现在插值参数的选取和确定依赖概率统计原则[11-13].

不确定性插值方法主要包括克里金(Kriging)方法和随机模拟方法.多点信息统计法(multiple-point statistics, MPS)是目前随机模拟的主流.通过再现高阶统计量,MPS能够从训练图像中捕捉复杂的特征样式并把它们复制到待模拟区域中,从而获得最终模拟结果[14-15].

在MPS重建数据过程中,训练图像的模式特征决定了模拟结果,但这些模式往往维数较高,数据处理较为困难.因此,模式降维问题成为MPS中的研究热点.一部分主流MPS方法,如过滤器随机模拟(filter-based stochastic simulation, FILTERSIM)[15]和距离模式随机模拟(distance-based pattern simulation, DISPAT)[16],将数据降维引入到其随机模拟过程中.但是,这些方法都采用线性降维处理模式数据,而真实情况下的数据并非都以线性形式存在着.如果空间数据处于非线性状态却使用线性方法降维,那么将会严重降低随机模拟的质量.另外,如果把线性降维当作非线性降维的一种特殊情况[17-18],那么基于空间数据非线性降维的随机模拟具有更广泛的一般性,可同时用于线性和非线性的空间数据重建.

条件数据对模拟结果的影响很大,而条件数据又可以分为硬条件数据和软条件数据.硬条件数据是已知的精确采样点数据,但可能数量很少.与硬条件数据相对应的是软条件数据.软条件数据总体上能够比较准确地反映所研究变量的变化趋势,但精度较差.在许多领域里,由于受到客观条件或技术水平限制,所能得到的硬条件数据非常有限,但是可以获得相对比较丰富的软条件数据.例如在石油勘探过程中,所能获得的硬条件数据(井位数据)往往非常少,而有关所研究对象的软条件数据(如地质解释和地震资料等)却相对较为丰富.如图1(a)表示勘探得到的井位数据,其中黑色和白色点分别表示砂岩(sand)和页岩(shale)井位的分布,是一种硬条件数据.图1(b)为对应区块的地震资料,是页岩分布概率,可作为软条件数据.可见硬条件数据的数量相对较少,如果能充分利用较为丰富的软条件数据,那么必然会提高所建模型的精度.

本文基于训练图像的非线性降维,提出一种利用多点信息统计法重建空间数据的方法,可以分别在结合使用软硬条件数据,只有硬条件数据和无条件数据情况下实现空间数据重建.由于本方法通过捕获训练图像的内在结构特征进行数据重建,因此适用于条件数据较少或没有条件数据情况下的数据重建.虽然重建结果具有随机性和不确定性,但是它们能在已知条件数据和先验模型基础上提供未来数据发展趋势的预测,具有一定实际意义.

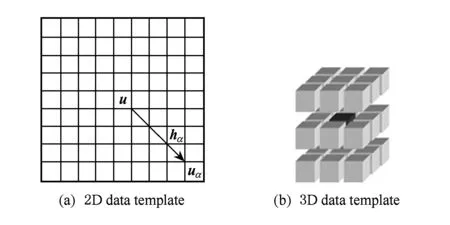
Fig. 2 Data template.图2 数据模板

1 MPS中的一些基本概念

设数据模板为τD,它是由D个向量组成的几何形态,τn={hα;α=1,2,…,D}.设模板中心位置为u,模板其他位置uα=u+hα(α=1,2,…,D).图2(a)是一个9×9节点组成的二维模板,uα由中心点u和80个向量hα所组成,各向量用网格节点表示.而在三维空间中数据模板的定义也是适用的,图2(b)是由3×3×3体素组成的三维模板,模板中心点u用黑色表示,其周围的各三维节点表示各个向量的位置,用浅灰色表示.注意本文的“节点”表示二维平面的像素或者三维空间的体素.假设变量S可以取K个状态值,即有状态值的集合{sk,k=1,2,…,K}.令d(uα)表示在uα的状态值.为了获得在某个向量u的状态值,选取离其最近的D个数据作为模拟时的条件数据.D个条件数据和它们的几何结构组成了“数据事件”,记为dD[19]:

dD={d(uα)=skα,α=1,2,…,D,kα∈[1,K]},

(1)

式(1)代表D个向量在uα位置的S(u1),S(u2),…,S(uD)分别为某个状态值sk.

图3(a)(b)所示为图2(a)的二维数据模板所捕获的2个数据事件,数据模板中包含3种灰度的节点:深灰、浅灰和白色节点.深灰和浅灰节点表示2种已知数据，白色节点为未知数据.同理,图3(c)(d)所示为图2(b)的三维数据模板所捕获的2个数据事件.其中,待模拟点u仍然位于3×3×3数据模板的中心,用黑色表示.深灰色节点表示已知数据点，浅灰色节点表示未知数据.

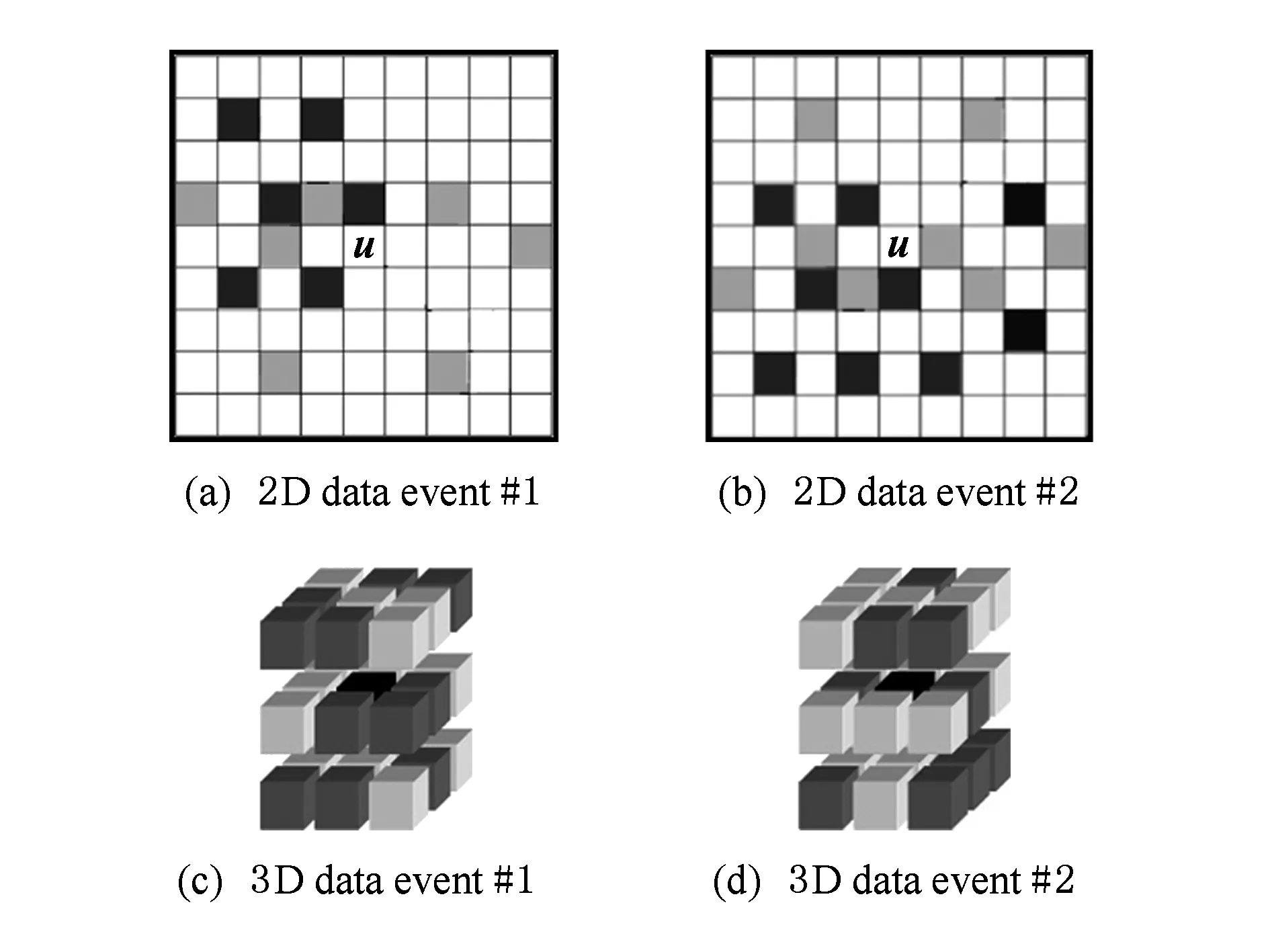
Fig. 3 2D data event and 3D Data event.图3 二维数据事件和三维数据事件

2 方法核心思想

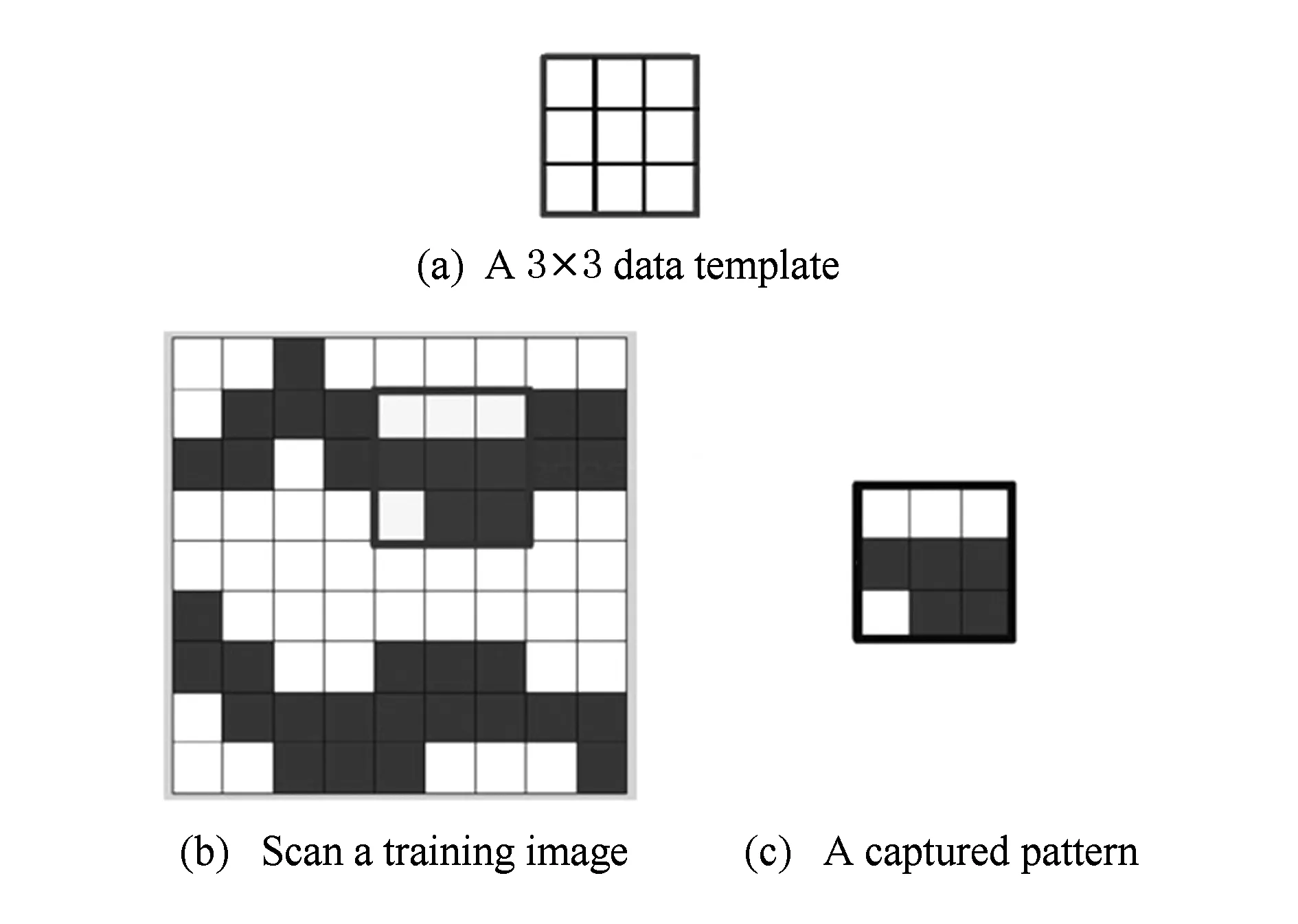
Fig. 4 Capture a pattern in a training image.图4 捕获训练图像中的一个模式

本文方法主要由4个部分组成:建立训练图像模式库、模式的降维、模式的分类和模式的提取.各部分详细内容分别介绍于2.1至2.4节.

2.1 建立训练图像的模式库

利用数据模板扫描训练图像来捕获数据事件,这些数据事件被称为“模式”,而这些模式包含了训练图像的结构特征.例如图4(a)是一个3×3的数据模板；图4(b)是利用数据模板扫描一个二维训练图像；图4(c)是捕获的一个模式.如果按照每次移动一个节点,从左到右、从上到下进行扫描,那么就可以获得训练图像全部的模式库,如图5所示.对于三维训练图像同理可以建立类似的模式库.

Fig. 5 Build a pattern database from a training image.图5 获取训练图像的模式库

设TI(u)表示以u为中心的模式,ti(u+hi)表示u+hi位置的属性值,那么有：

TI(u)=(ti(u+h1),ti(u+h2),…,ti(u+hD)).

(2)

可见模式TI(u)和数据模板尺寸相同,如果将各个模式从训练数据中抽取出来形成模式库,那么与具体位置u无关,此时可设模式库中的模式个数为Npat,那么第k个模式可以表示为

patk=(patk(h1),patk(h2),…,patk(hD)),

k=1,2,…,Npat,

(3)

其中,patk(hi)与ti(u+hi)(i=1,2,…,D)一一对应.整个模式库patDb可以表示为

patDb=(pat1,pat2,…,patNpat),

(4)

其中，每个patk(k=1,2,…,Npat)可以视为模式空间中的一个点.

2.2 模式的降维

降维方法可分为线性降维和非线性降维.线性降维方法主要用来对线性数据降维,代表性方法有主成分分析(principal component analysis, PCA)和多维尺度变换(multi-dimensional scaling, MDS)等.然而现实世界的许多数据处于非线性结构,采用线性降维方法难以处理非线性数据.本文采用等距特征映射(isometric mapping, ISOMAP)实现模式的非线性降维[20-21].

每个模式patk(k=1,2,…,Npat)含有D个分量,可以视其维数为D.本方法通过ISOMAP将patDb中的各个模式patk降维到d(d≪D)维空间.降维后得到的低维数据集设为Y=(y1,y2,…,yNpat)(其中yk∈d,k=1,2,…,Npat),即样本个数不变,每个样本的维数从D变为d.利用ISOMAP降维的步骤如下[21]:

1) 构造模式近邻图G.计算模式库patDb中所有模式对(pati,patj)间的欧氏距离,记为dE(pati,patj)：

(5)

比较欧氏距离,确定每个模式的k个最相似模式；构造模式近邻图G,图G中的节点和各模式一一对应.边代表近邻关系,即如果pati和patj是相似模式,G中对应节点i和j用边连接,否则断开.边权值用模式间欧氏距离dE(pati,patj)表示.

2) 计算模式间的最短路径dM(pati,patj).当图G中存在边(i,j)时,设最短路径dM(pati,patj)=dE(pati,patj),否则dM(pati,patj)=∞,对于p=1,2,…,Npat：

dM(pati,patj)=min{dM(pati,patj),

dM(pati,patp)+dM(patp,patj)}.

(6)

最短路径距离阵可表示为DM=(dM(pati,patj))2,i,j=1,2,…,Npat.

3) 计算低维映射.计算对称阵:

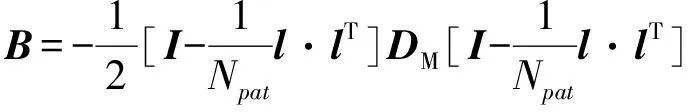
(7)

其中，I是Npat阶单位阵,l是元素全为1的Npat维列向量.低维空间的维度为d,则求取矩阵B的d个最大的特征值λ1≥λ2≥…≥λd,对应的特征向量是α1,α2,…,αd,则可得降维后的各个模式：

Y=(y1,y2,…,yNpat)T=

(8)

至此获得patDb={patk}(patk∈D,k=1,2,…,Npat)的低维映射Y={yk}(yk∈d,k=1,2,…,Npat),数据从高维空间D映射到低维空间d.低维空间的维数d可以通过最大似然估计法获得,具体步骤可见文献[22].

2.3 模式的分类

在完成训练图像中模式的降维后,需要对获取的低维模式进行分类.对这些模式采用一种基于密度的聚类方法(density-based spatial clustering of applications with noise, DBSCAN)进行分类[23].其主要思想是：只要邻近区域的密度(对象的数目)超过某个阈值,就继续执行聚类操作.

在利用DBSCAN划分模式空间后,获得若干“子空间”,每个子空间命名为Cell.图6所示是一个二维空间被划分为若干个Cell,其中包含一个空的Cell,每个黑点表示一个降维后的模式.对于每个Cell,可以定义一个与数据模板相同形状的“平均模板”,称为Prototype. Prototype是属于该Cell的所有模式在原高维空间中各节点位置的均值.例如,图7(a)是一幅训练图像(150×150像素),包含页岩和砂岩2种状态值,图7(b)表示属于一个Cell的所有15个模式(13×13像素),图7(c)表示该Cell对应的Prototype(13×13像素).本质上Prototype可以视为每个Cell中所有模式的均值,是该Cell所有模式的“代表”.

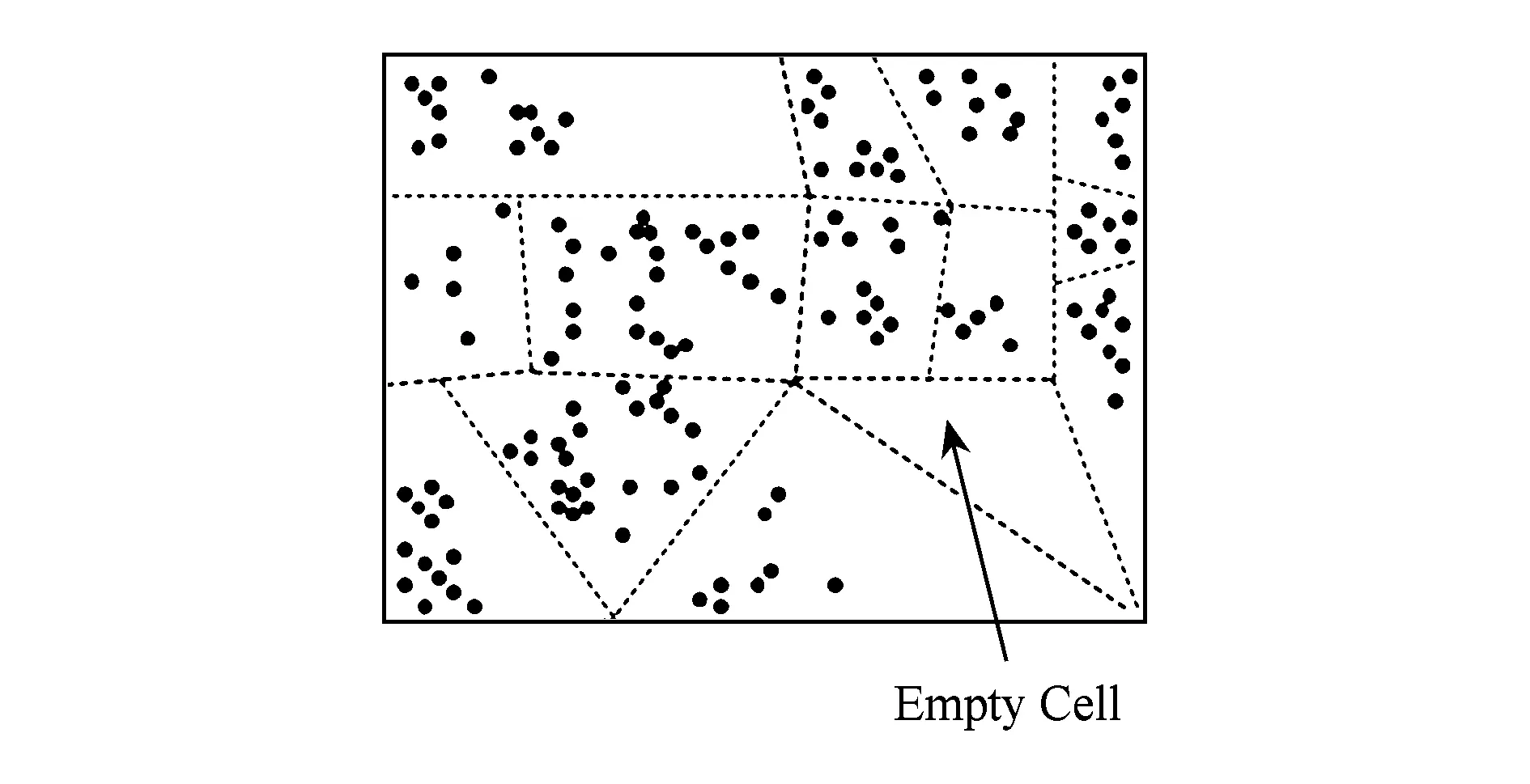
Fig. 6 Illustration of separating pattern space into some Cells.图6 划分模式空间成各个Cell

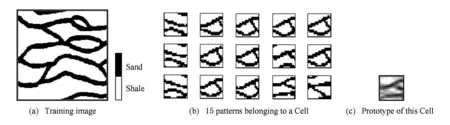
Fig. 7 Illustration of a Prototype.图7 Prototype示意图

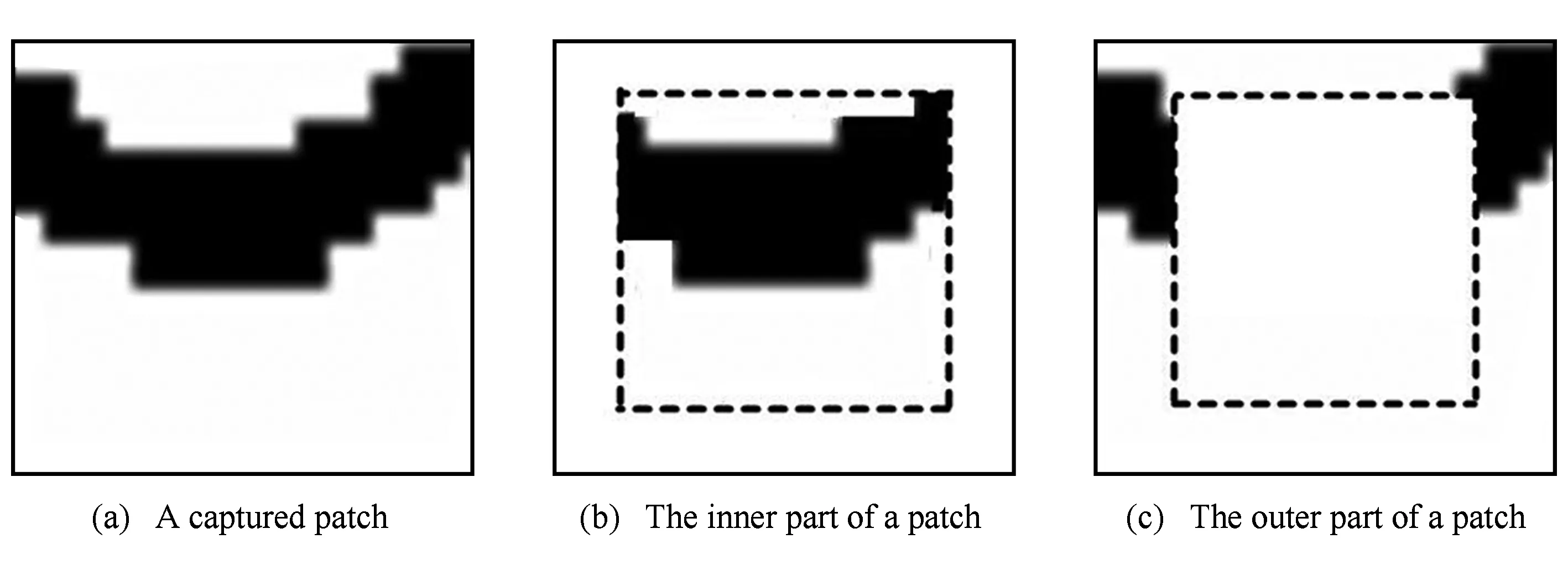
Fig. 8 A patch and its inner part and outer part.图8 patch及其inner和outer部分

Prototype的值prot(l)(hα)表示属于一个Cell中的所有图案在各个hα位置的均值,定义为

(9)

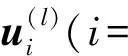
protl=(prot(l)(h1),prot(l)(h2),…,prot(l)(hD)),

(10)

其中，l=1,2,…,L,protl可以视为第l个模式类的平均模式.

2.4 模式的提取

利用扫描训练图像时使用的数据模板扫描待重建区域,检索以未知点u为中心的数据事件内的所有已知节点,这些点视为硬条件数据.设已知硬条件数据点数目为n′≤D.提取的训练图像的模式(称为patch)本质上即训练图像内的图像块.将patch分为2个部分：inner部分和outer部分.它们可以作为其他后继节点重建时的硬条件数据.不同之处在于,inner部分会被“固定”为重建结果,不会再对其进行模拟；而patch的outer部分不仅作为其他节点模拟的条件数据,而且该部分的所有节点会被当作未知点重新模拟.如图8(a)是一个patch,图8(b)(c)分别是其inner部分(虚线内部分)和outer部分(虚线外部分).如果一个patch的inner部分被设定得比较大,那么重建速度会较快,但是容易产生局部的不连续性；反之,较小的inner部分会导致重建速度比较慢,但是重建效果会较好.

设t表示数据类型,则patch中一共可能有3种数据：

1)t=1,原始硬条件数据,它们被分配到各节点位置上；

2)t=2,已经模拟过的节点,它们被固定为硬条件数据,即patch的inner部分(不包含inner部分内的原始硬条件数据)；

3)t=3,通过“粘贴”Cell中的patch而已知的节点,但这些点会被重新模拟,即patch的outer部分(不包含outer部分内的原始硬条件数据).

另外定义“距离函数”如下：

(11)

其中，t=1,2,3;l=1,2,…,L；dis(d(uα),protl)表示求取数据事件d(uα)和protl中对应的已知节点间的距离.每种节点会根据其类型而给定一个权值ω(t),表示其在求取距离函数中的重要性,注意有ω(3)≤ω(2)≤ω(1).可见原始硬条件数据点在距离函数中的作用最大.

假设以u为中心的硬条件数据事件hd(uα)与各个protl之间的距离可以表示为

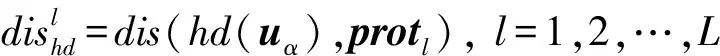
(12)

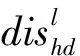
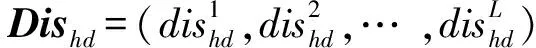
(13)

如果在位置u处也对应存在一个以u为中心的软条件数据事件sd(uα),它与各个protl之间的距离可以表示为

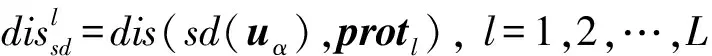
(14)

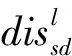
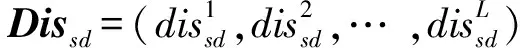
(15)

由式(15)可得整合软硬条件数据的数学模型,即求取软硬条件数据情况下数据事件与protl之间的距离向量：

Distotal=perhd×Dishd+μ×Dissd,

(16)

其中,perhd表示在数据模板中已知硬条件数据的节点数占模板总节点数的百分比,因为当硬条件数据较多时,其能提供的辅助判断信息会增加,权值相应变大；而μ(0≤μ≤1)是表示软数据准确性的权值,它的取值取决于人们对软数据准确性的主观意见.当μ=0,表示完全忽略软数据；而当μ=1,表示完全信任软数据.另外,Dishd和Dissd要进行归一化处理,即令其取值范围为[0,1].

假设有:

(17)

则Distotal可以表示为

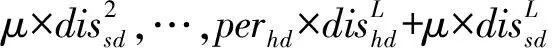
(18)

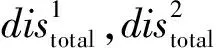
3 重建过程的完整流程

根据初始条件数据的不同,节点u的重建可以分为4种情况:1)无条件数据模拟(称为情况C1);2)只有硬条件数据情况下的模拟(称为情况C2);3)软条件数据和硬条件数据同时存在时的模拟(称为情况C3);4)只有软条件数据情况下的模拟(称为情况C4).第2节对本方法各核心部分作了重点介绍,本节将第2节部分整合起来,形成本方法的完整流程:

1) 利用数据模板扫描训练图像，构建模式库patDb.

2) 利用ISOMAP对模式库中的模式进行降维.

3) 采用DBSCAN对降维后的模式进行分类.

4) 定义一条随机访问路径，对重建区域内的未知节点进行访问.

5) 检查访问路径上的待模拟节点u是已知的硬条件数据还是已模拟节点.如果是已知的硬数据或已模拟节点，则对随机路径上的下个节点进行判定；否则转向步骤6).

6) 检索以u为中心的数据模板内的硬条件数据(设数目为n′)和对应的软条件数据.根据条件数据的不同,提取patch的方法分为4种情况:

① 如果条件数据属于情况C1(即n′=0,无软条件数据)，那么随机地从训练图像模式库patDb中随机提取一个patch，然后将该patch直接复制到以当前模拟节点u为中心的重建区域.

② 如果条件数据属于情况C2(即n′>0,无软条件数据)，即以u为中心的硬数据事件非空，那么就在训练图像所有的protl中利用式(16)寻找与当前数据事件最接近的protl.一旦该protl被确定,则从与之对应的Cell中随机提取一个patch,然后将它复制到以当前模拟节点u为中心的重建区域.注意在计算式(16)时,只能获得硬距离Dishd,软距离Dissd不存在.

③ 如果条件数据属于情况C3(即n′>0,且有软条件数据)，那么同时有软硬条件数据,此时直接利用式(16)获得与当前数据事件最接近的protl,然后从与该protl对应的Cell中随机提取一个patch复制到重建区域.

④ 如果条件数据属于情况C4(即n′=0,仅有软条件数据)，也是利用式(16)获得与当前数据事件最接近的protl,然后从与该protl对应的Cell中随机提取一个patch复制到重建区域.在重建的初始阶段时,式(16)中仅存在软距离Dissd,但是随着重建过程的进行,已模拟节点不断增加,这些节点成为后继节点模拟的硬条件数据.那么此时变为软硬条件数据结合情况下的重建.

7) 将patch复制到重建区域后,再将patch的部分节点固定为inner部分,该patch的其他节点作为outer部分.

8) 重复步骤5)～7)，继续对其他节点进行模拟，直到随机路径上的所有节点被模拟完毕.

本方法的流程图如图9所示.值得注意的是,由于情况C3下硬条件数据通常较为稀疏,即在大多数情况下重建区域内只有软条件数据,因此本文将情况C3和C4视为同一种情况,并且在实验部分仅对情况C1,C2,C3进行测试.

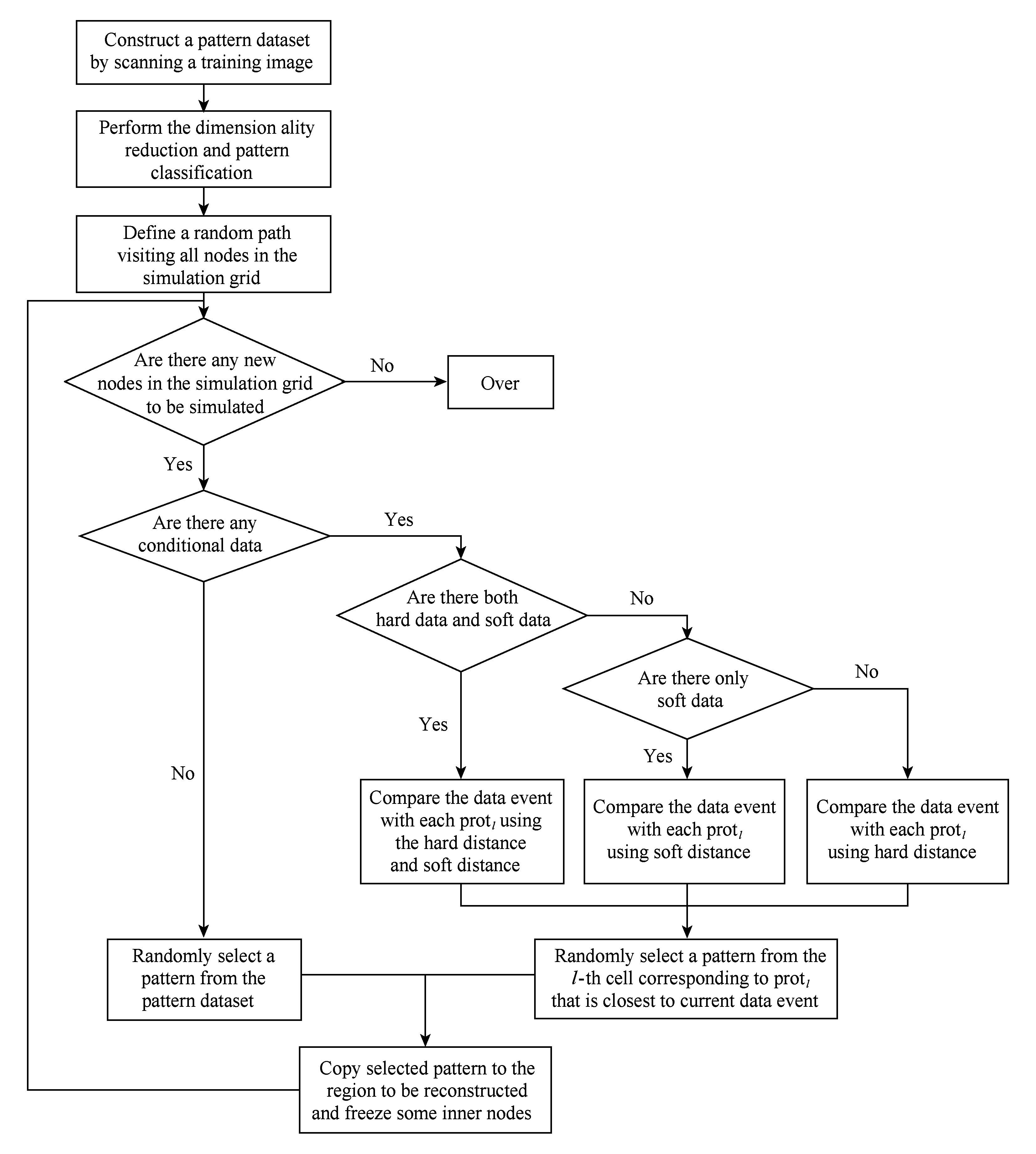
Fig. 9 Flow chart of the proposed method.图9 本文方法流程图

4 实验结果及分析

4.1 重建质量的评价标准

对于评价重建结果优劣的标准,随机重建与一般重建方法有较大的不同.一般重建方法中的重建数据与原始数据的相似度是由两者在每个相同位置具有相同状态值元素的比例决定的.在一般重建方法中,该比例越高,重建相似度就越高,但是这个判定标准对于随机重建并不适用.随机重建并不要求随机模拟结果与训练图像完全一致,它的真正作用体现在捕捉训练图像的结构特征,并将这些特征复制到重建数据中.随机重建可以给出多个模拟结果,这些结果是对训练图像结构特征的反映.重建效果的优劣在于这些结构特征是否被复制到重建数据中.

因此,本文评价重建结果时并不直接比较重建结果和训练图像是否相同,而是通过多个重建结果的均值和方差分布以及变差函数来衡量.变差函数能够反映变量在某个方向上空间结构变化的相关性和变异性.如果2幅图像中的某个属性值在同一个方向上具有相似的变差函数曲线,那么可以说明这2幅图像中的该属性值在此方向上具有相似的结构特征；反之,该属性值在此方向上的结构差异较大.变差函数[24]的定义为

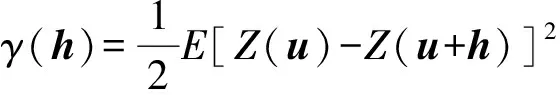
(19)

其中,Z(u)和Z(u+h)分别表示位置u和u+h处的变量状态值,h表示距离向量,E表示求数学期望值.

4.2 重建实验

为了验证本方法有效性,分别对三维离散型数据和三维连续型数据进行重建实验.所有实验都是在Intel core i3-4160T (3.1 GHz CPU)和4 GB DDR3内存环境下运行的.式(11)中的权值ω(1)=0.5,ω(2)=0.3,ω(3)=0.2.如第3节所述,由于将C3和C4视为同一种情况,故以下实验只分别对C1,C2,C3这3种情况下的重建进行测试.

4.2.1 三维离散型数据重建

首先实验三维离散型数据的重建效果.图10(a)是一幅多孔介质(碳酸岩)体数据训练图像(80×80×80体素),包含孔隙和骨架2种状态值,孔隙所占百分比(孔隙度)为0.201;图10(b)是训练图像的截面图(3个截面分别为X=40,Y=40和Z=40);图10(c)是训练图像的孔隙结构图.图11是硬条件数据,分别是孔隙点和骨架点,其中孔隙点比例为0.182,设重建区域为80×80×80体素.由于多孔介质内部只存在孔隙和骨架2种状态值,因此重建区域内孔隙和骨架在某个体素位置的概率之和为1.图12(a)(b)分别是孔隙和骨架分布的概率图,作为重建时的软条件数据.根据最大似然估计法,设置低维空间的维数d=9[22].情况C1,C2,C3下重建结果分别如图13～15所示.可见,3种情况下基本都可以重建孔隙和骨架的结构特征.对情况C1～C3下各实现10次重建,设孔隙状态值为1,骨架状态值为0,则可得3种情况下重建结果均值和方差,如图16和图17所示.3种情况下均值(即孔隙度)见表1所示.求取的方差只有6种取值:0,0.09,0.16,0.21,0.24,0.25,各体素位置的方差值分布如图18所示.可以看出C3重建结果的方差值最小,说明C3重建结果的波动性最小.C1～C3重建图像均值和训练图像的变差函数曲线如图19所示,可见训练图像与C3重建结果的变差函数最为接近.情况C1～C3下10次重建的时间和占用的最大内存如表2所示,可见C3时使用的时间和内存最大.以上实验表明,结合使用软硬数据能够提高重构质量，但是会占用较多的CPU时间和内存.

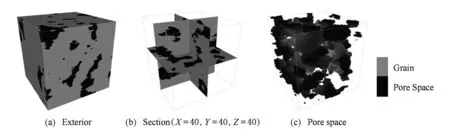
Fig. 10 Training image of carbonatite.图10 碳酸岩训练图像

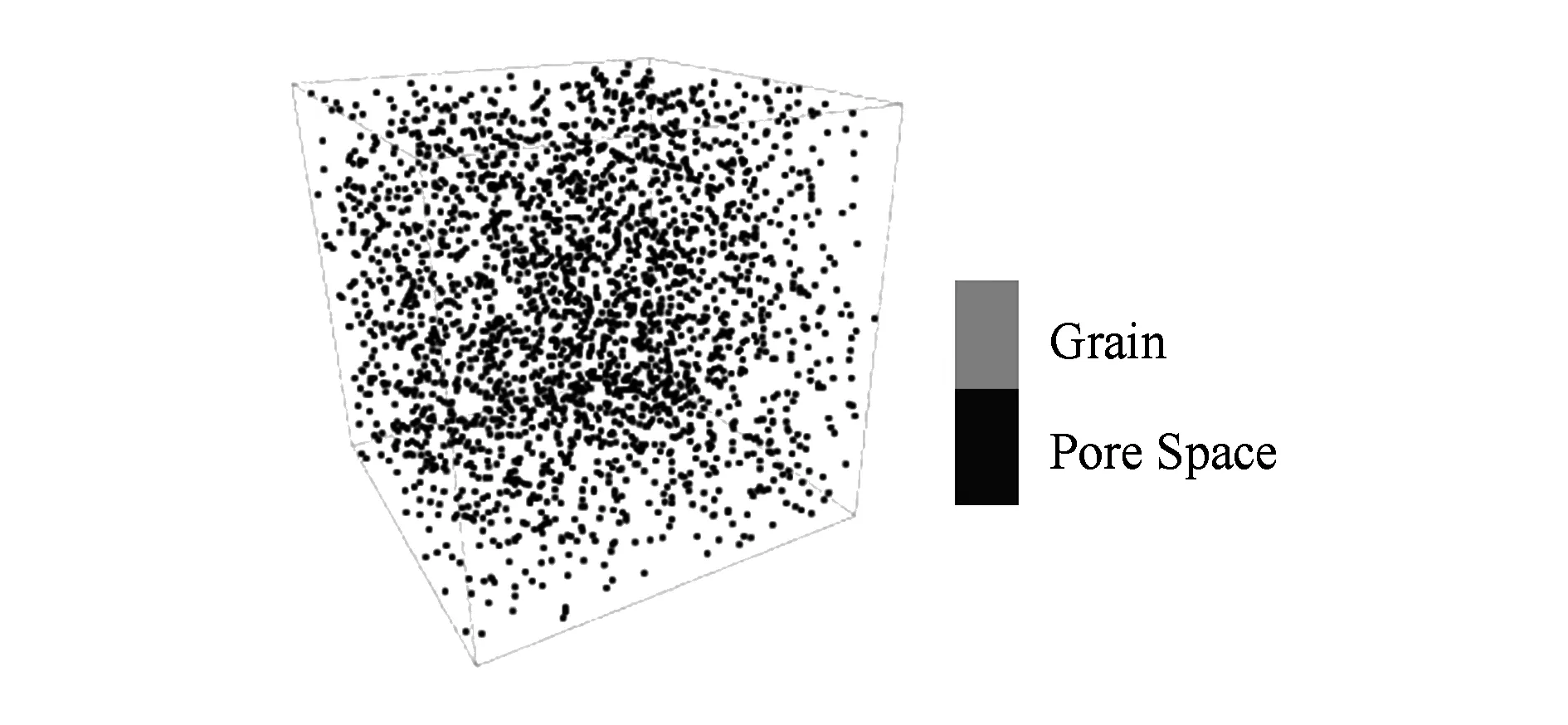
Fig. 11 Hard conditional data of carbonatite.图11 碳酸岩硬条件数据

Fig. 12 Probability distribution of pore spaces and grains.图12 孔隙和骨架分布的概率图

Fig. 13 Reconstructed results of C1.图13 C1重建结果

Fig. 14 Reconstructed results of C2.图14 C2重建结果

Fig. 15 Reconstructed results of C3.图15 C3重建结果

Fig. 16 Average of 10 times of reconstructed carbonatite results under three conditions.图16 3种情况下的碳酸岩重建结果均值

Fig. 17 Variance of 10 times of reconstructed carbonatite results under three conditions.图17 3种情况下的碳酸岩重建结果方差

Table 1 Average of the Training Image and Reconstructed Carbonatite Images with C1, C2 and C3

表1 训练图像、C1,C2,C3情况下重建的碳酸岩图像均值

Fig. 18 Variance distribution at each voxel location under three conditions of C1, C2 and C3.图18 C1,C2,C3情况下各体素位置的方差值分布

Table 2 Maximum Time and Memory for Reconstructing Ten Carbonatite Images with C1, C2 and C3

表2 C1,C2,C3情况下重建10幅碳酸岩图像的时间和占用的最大内存

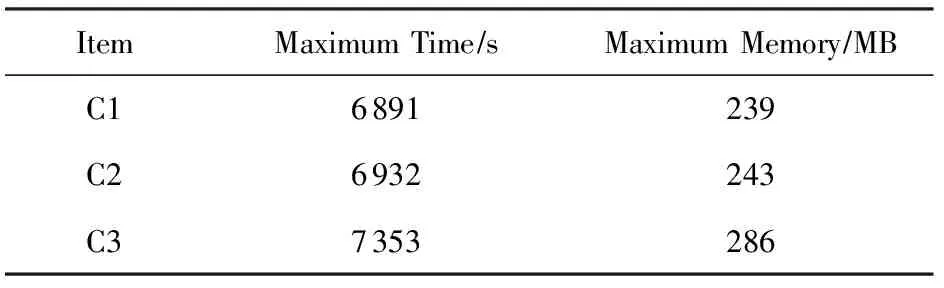
ItemMaximumTime∕sMaximumMemory∕MBC16891239C26932243C37353286

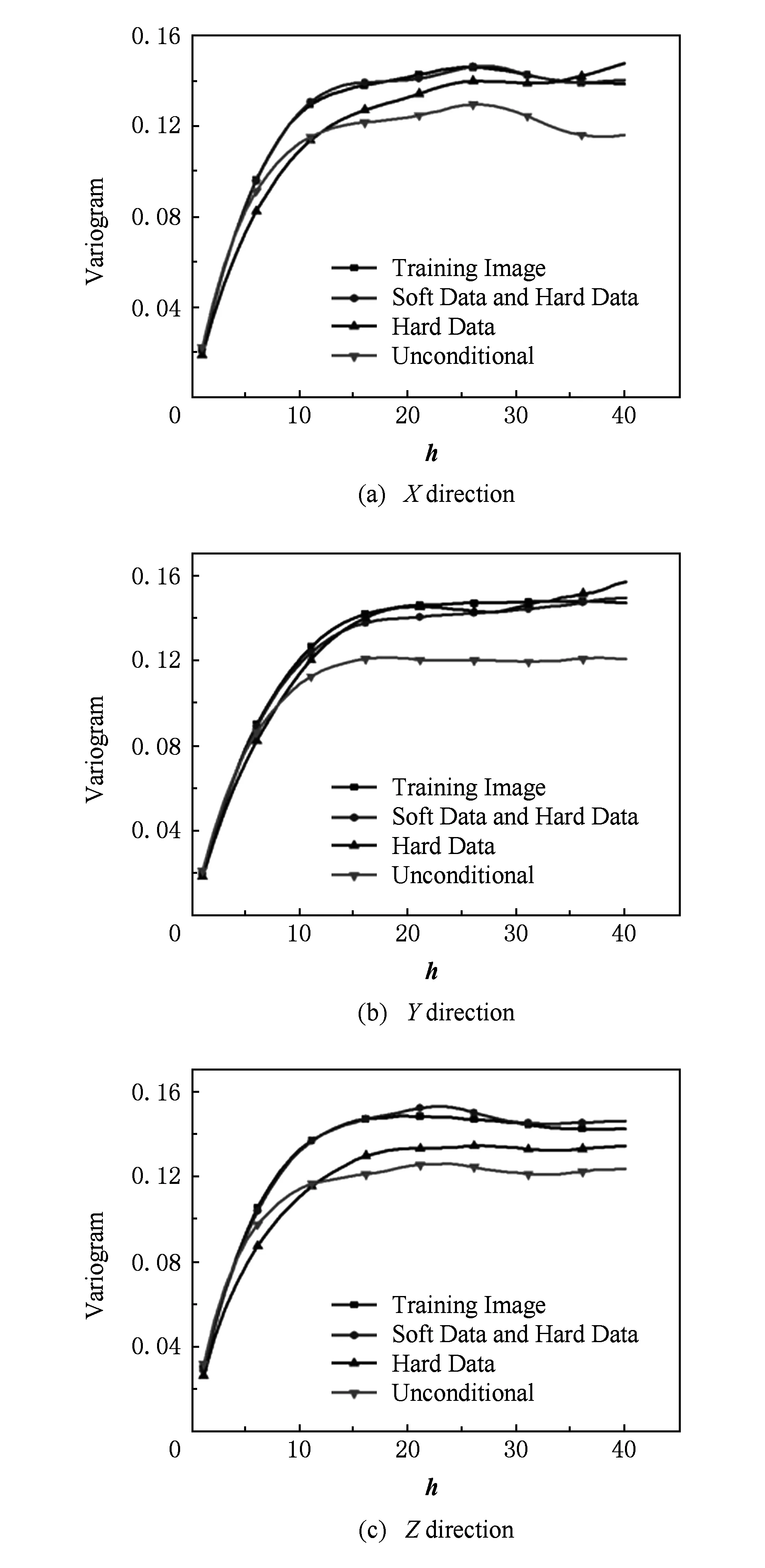
Fig. 19 Variogram curves of the training image and average reconstructed images of carbonatite.图19 碳酸岩训练图像和重建图像均值的变差函数

4.2.2 三维连续型数据重建

进一步实验三维连续型数据的重建效果.图20(a)是一幅渗透率体数据的训练图像(50×50×20体素,均值为1.634 Darcy),设重建区域也为50×50×20体素.重建所使用的硬数据与软数据分别如图20(b)(c)所示.硬条件数据占全部重建区域体素点的1%.情况C1～C3下重建结果分别如图21～23所示.在C1～C3这3种情况下各实现10次重建,则可得3种情况下重建结果均值和方差,如图24和图25所示.各情况下均值见表3所示.各体素位置的方差值分布如图26所示,可见C3重建结果的方差值最小,说明C3情况下重建结果的波动性最小.C1～C3重建图像均值和训练图像的变差函数曲线如图27所示,说明C3的重建结果最接近训练图像.C1～C3情况下10次重建的时间和占用的最大内存如表4所示,可见3种情况的差异不大,但是C3情况下的重建时间和内存占用量最多.以上实验再次证明,结合使用软硬数据有助于提高重构质量,但是也会占用较多的CPU时间和内存.

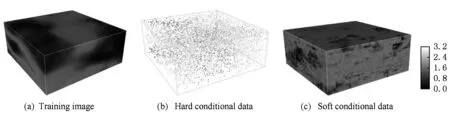
Fig. 20 Training image, hard and soft conditional data for reconstructing permeability image.图20 渗透率图像重建所使用的训练图像和软硬条件数据

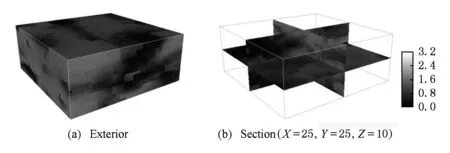
Fig. 21 Reconstructed results of C1.图21 C1重建结果

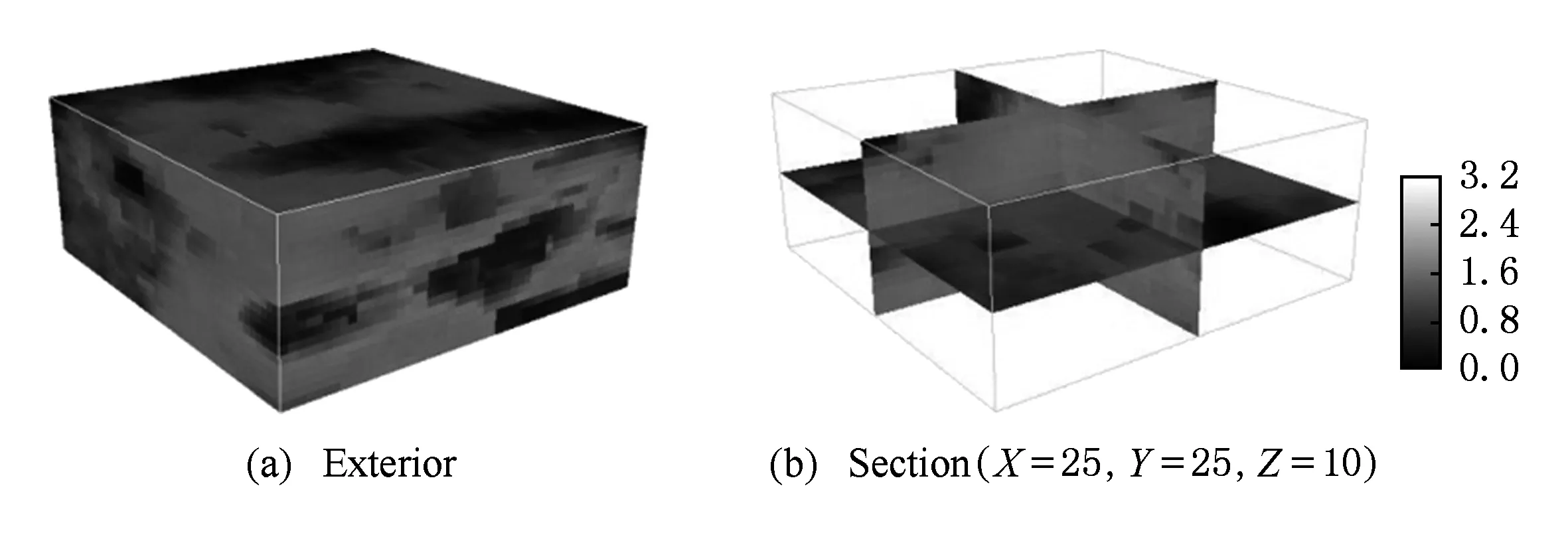
Fig. 22 Reconstructed results of C2.图22 C2重建结果

Fig. 23 Reconstructed results of C3.图23 C3重建结果

Fig. 24 Averages of 10 times of reconstructed permeability results under the conditions of C1, C2 and C3.图24 C1,C2,C3情况下的渗透率重建结果均值

Fig. 25 Variance of 10 times of reconstructed permeability images under the conditions of C1, C2 and C3.图25 C1,C2,C3情况下的渗透率重建结果方差

Table 3 Average of the Training Image and the Reconstructed Permeability Images with C1, C2 and C3

表3 训练图像、C1,C2,C3情况下重建的渗透率图像均值

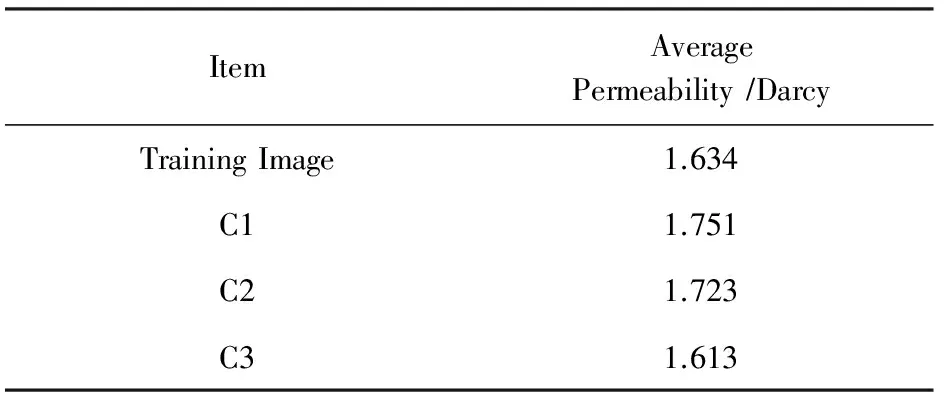
ItemAveragePermeability∕DarcyTrainingImage1．634C11．751C21．723C31．613

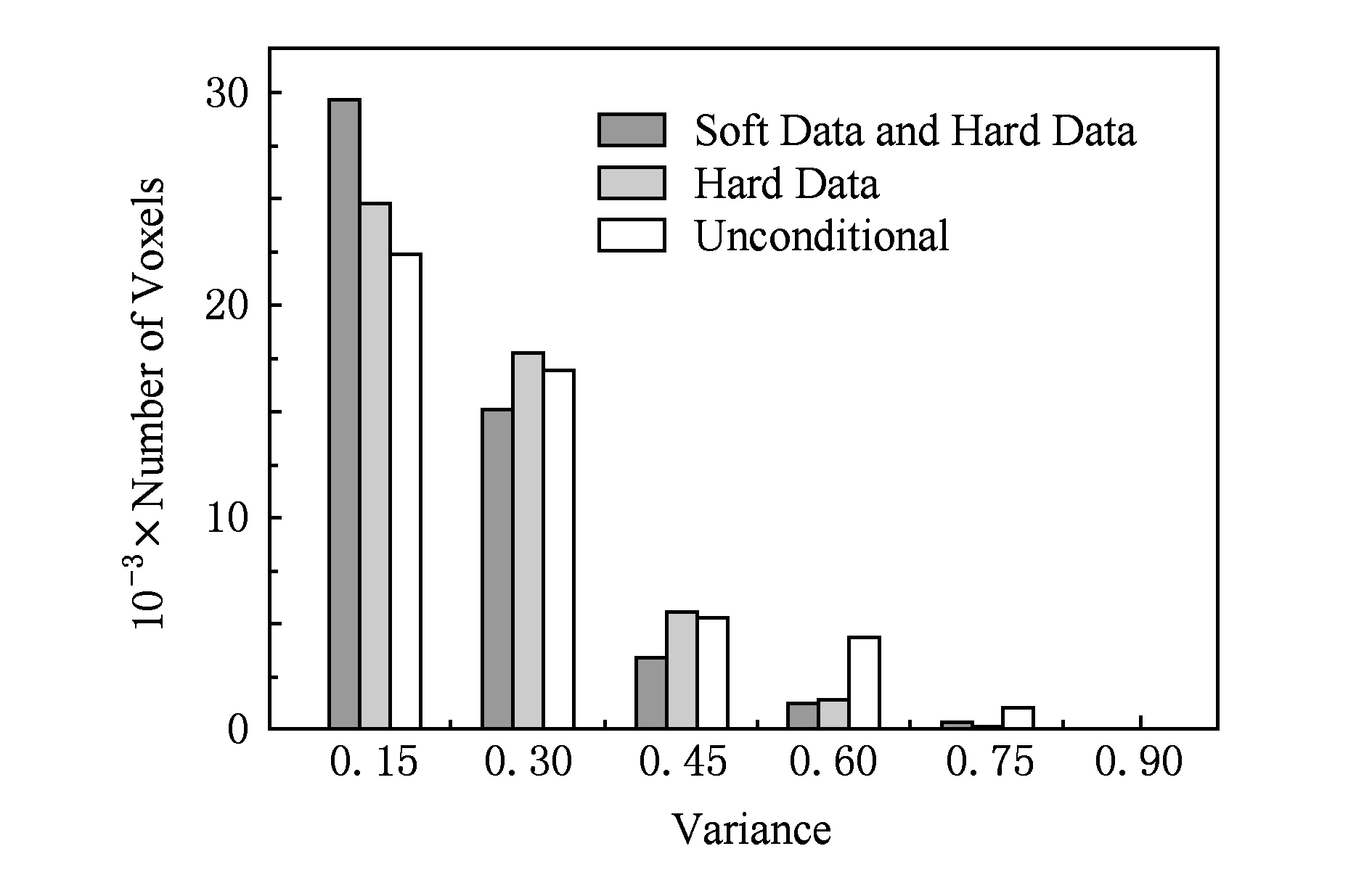
Fig. 26 Variance distribution at each voxel location under the conditions of C1, C2 and C3.图26 C1,C2,C3情况下各体素位置的方差值分布

Table 4 Maximum Memory and Time for Reconstructing Images with C1, C2 and C3

表4 C1,C2,C3情况下重建图像的时间和最大内存

4.3 与FILTERSIM和DISPAT的比较

Fig. 28 Reconstructed results of FILTERSIM.图28 FILTERSIM重建结果

如引言所述,FILTERSIM和DISPAT是典型的基于线性降维的MPS方法.现利用FILTERSIM和DISPAT与本方法进行对比.实验样本即4.2.1节采用的碳酸岩.对FILTERSIM和DISPAT进行结合软硬条件数据情况下(即C3情况)的模拟,即采用图10的训练图像、图11的硬条件数据和图12的软条件数据.分别利用FILTERSIM和DISPAT进行10次重建,每个重建结果为80×80×80体素,一些重建结果的孔隙结构如图28和图29所示.可见FILTERSIM和DISPAT能较好地再现孔隙结构,只是FILTERSIM生成的孔隙的连通性较好,易于形成较大范围的连通孔隙空间;而DISPAT生成的孔隙空间连通性稍差,因此大范围连通的孔隙较少.训练图像和3种方法(本文方法、FILTERSIM和DISPAT)重建结果均值的变差函数参见图30所示.可见本文方法重建结果的变差函数和训练图像变差函数最为接近.FILTERSIM和DISPAT生成上述10个结果的时间和内存占用如表5所示.与表2的C3(即同时使用软硬条件数据)情况相比,可见本方法具有计算速度和内存使用的优势.

Fig. 29 Reconstructed results of DISPAT.图29 DISPAT重建结果

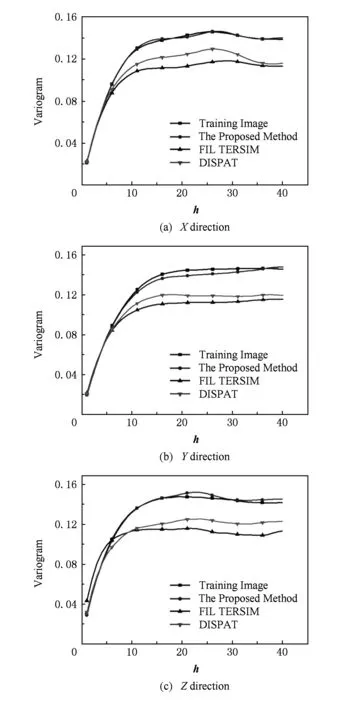
Fig. 30 Variograms of the training image and average reconstructed images using three methods.图30 训练图像和3种方法重建图像的平均变差函数

Table 5 Maximum Time and Memory for Reconstructing Ten Carbonatite Images using FILTERSIM and DISPAT

表5 FILTERSIM和DISPAT重建图像的时间和最大内存

5 总 结

重建区域内的条件数据对重建结果的准确性影响很大.当已知条件数据较少甚至没有条件数据时,非确定性插值方法是重建空间数据的有效手段.多点信息统计法是目前非确定性插值方法的重要分支.它从训练图像提取模式特征,并将其复制到待模拟区域,以完成对缺失空间数据的重建.但是训练图像往往包含大量非线性数据,传统多点信息统计法处理线性数据效果较好,但是并没有针对非线性数据提出具体的处理策略.一些基于降维分类思想的多点信息统计法只是采用线性降维方法来处理包括非线性数据在内的所有数据,这可能会造成空间数据重建质量的下降.

本文采用ISOMAP对训练图像中的模式数据进行降维处理.由于ISOMAP是一种非线性降维方法,因此适用于降低非线性数据的维度.如果把线性数据视为非线性数据的特殊情况,那么ISOMAP同样可以用于线性数据降维,这大大拓展了多点信息统计法的应用范围.基于MPS和ISOMAP提出在无条件数据,只有硬条件数据和结合软硬条件数据情况下的空间数据重建方法,实验验证了方法的有效性.又与传统采用线性降维的多点信息统计法(即DISPAT和FILTERSIM)进行比较,显示出采用非线性降维方法处理空间数据的优势.值得指出的是：虽然本方法采用的随机模拟会使得重建结果具有一定的不确定性并产生多种可能结果,但是这些结果都是在当前条件数据和先验模型下对未知区域数据的合理预测,对风险评测研究和分析决策均具有指导意义.

[1]Wang Wencheng. Research and realization of volume rendering in 3D data fields[D]. Beijing: Institute of Software, Chinese Academy of Sciences, 1998 (in Chinese)(王文成. 三维数据场体绘制技术的研究和实现[D]. 北京: 中国科学院软件研究所, 1998)

[2]Vedadi F, Shirani S. A MAP-based image interpolation method via viterbi decoding of Markov chains of interpolation functions[J]. IEEE Trans on Image Processing, 2014, 23(1): 424-438

[3]Delibasis K K, Kechriniotis A I, Assimakis N D. New closed formula for the univariate hermite interpolating polynomial of total degree and its application in medical image slice interpolation[J]. IEEE Trans on Signal Processing, 2012, 60(12): 6294-6304

[4]Alpay D, Lewkowicz I. Interpolation by polynomials with symmetries[J]. Linear Algebra and Its Applications, 2014, 456: 64-81

[5]Wang Yunsen, Yang Dongsheng, Liu Yinzhong. A real-time look-ahead interpolation algorithm based on Akima curve fitting[J]. International Journal of Machine Tools & Manufacture, 2014, 85: 122-130

[6]Matej S, Kazantsev I G. Fourier-based reconstruction for fully 3-D PET: Optimization of interpolation parameters[J]. IEEE Trans on Medical Imaging, 2006, 25(7): 845-854

[7]Angelo L D, Stefano P D. C1 continuities detection in triangular meshes[J]. Computer-Aided Design, 2010, 42: 828-839

[8]Chen K, Lorenz D A. Image sequence interpolation based on optical flow, segmentation, and optimal control[J]. IEEE Trans on Image Processing, 2012, 21(3): 1020-1030

[9]Pan Rijing. Quadratic B-spline interpolation curves with tangent constraints on data points[J]. Chinese Journal of Computers, 2007, 30(12): 2132-2141 (in Chinese)(潘日晶. 满足数据点切向约束的二次B样条插值曲线[J].计算机学报, 2007, 30(12): 2132-2141)

[10]Paiement A, Mirmehdi M, Xie X, et al. Integrated segmentation and interpolation of sparse data[J]. IEEE Trans on Image Processing, 2014, 23(1): 110-125

[11]Jing Minggang, Wu Jitao. Fast image interpolation using directional inverse distance weighting for real-time applications[J]. Optics Communications, 2013, 286: 111-116

[12]Du Yi, Zhang Ting, Lu Detang, et al. An interpolation method using an improved Markov model[J]. Journal of Computer Research and Development, 2012, 49(3): 565-571 (in Chinese)(杜奕, 张挺, 卢德唐, 等. 一种基于改进的Markov模型的插值方法[J].计算机研究与发展, 2012, 49(3): 565-571)

[13]Wang Guozhao, Fang Lincong. On control polygons of quartic pythagorean hodograph curves[J]. Computer Aided Geometric Design, 2009, 26: 1006-1015

[14]Guardiano F, Srivastava M R. Multivariate geostatistics: Beyond bivariate moments[EB/OL]. (1993-03-21)[2014-03-02]. https://pangea.stanford.edu/ researchgroups/ scrf /sites /default /files

[15]Zhang Tuanfeng. Filter-based training pattern classification for spatial pattern simulation[D]. Palo Alto: Stanford University, 2006

[16]Honarkhah M. Stochastic simulation of patterns using distance-based pattern modeling[D]. Palo Alto: Stanford University, 2011

[17]Lei Yingke. The study of manifold learning algorithms and their applications[D]. Hefei: University of Science and Technology of China, 2011 (in Chinese)(雷迎科. 流形学习算法及其应用研究[D]. 合肥: 中国科学技术大学, 2011)

[18]Wang Yong. Manifold learning based classification and clustering approaches with their applications[D]. Changsha: National University of Defense Technology, 2011 (in Chinese)(王勇. 基于流形学习的分类与聚类方法及其应用研究[D]. 长沙: 国防科学技术大学, 2011)

[19]Zhang Ting, Lu Detang, Li Daolun, et al. Research on statistical information reconstruction of images based on multiple-point geostatistics integrating soft data with hard data[J]. Journal of Computer Research and Development, 2010, 47(1): 43-52 (in Chinese)(张挺, 卢德唐, 李道伦, 等. 基于软硬数据的多点信息统计法在图像统计信息重构中的应用研究[J]. 计算机研究与发展, 2010, 47(1): 43-52)

[20]Kim K, Lee D. Inductive manifold learning using structured support vector machine[J]. Pattern Recognition, 2014, 47: 470-479

[21]Tenenbaum B J, Silva V, Langford C J. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(22): 2319-2323

[22]Levina E, Bickel P J. Maximum likelihood estimation of intrinsic dimension[C] //Proc of Neural Information Processing Systems (NIPS 2005). Cambridge, MA: MIT Press, 2005: 777-784

[23]Ester M, Kriegel H P, Sander J, et al. A density-based algorithm for discovering clusters in large spatial databases[C] //Proc of Knowledge Discovery and Data Mining(KDD’96). Menlo Park: AAAI Press, 1996: 226-231

[24]Goovaerts P. Geostatistics for Natural Resources Evaluation[M]. New York: Oxford University Press, 1997:45-60

Du Yi, born in 1977. PhD and associate professor in Shanghai Polytechnic University. Member of China Computer Federation. Her main research interest is data mining.

Zhang Ting, born in 1979. PhD and associate professor in Shanghai University of Electric Power. His main research interest is image reconstruction.

Huang Tao, born in 1979. PhD and associate professor in the University of Science and Technology of China. His main research interest is high performance computing.

A Reconstruction Method of Spatial Data Using MPS and ISOMAP

Du Yi1, Zhang Ting2, and Huang Tao3

1(College of Engineering, Shanghai Polytechnic University, Shanghai 201209)2(CollegeofComputerScienceandTechnology,ShanghaiUniversityofElectricPower,Shanghai200090)3(DepartmentofModernMechanics,UniversityofScienceandTechnologyofChina,Hefei230027)

Conditional data influence the reconstructed results greatly in the reconstruction of spatial data. Reconstructed results often show a number of uncertainties when only sparse conditional data are available, so it is suitable to use indefinite interpolation to reconstruct spatial data. As one of the main indefinite interpolation methods, multiple-point statistics (MPS) can extract the intrinsic features of patterns from training images and copy them to the simulated regions. Because the traditional MPS methods using linear dimensionality reduction are not suitable to deal with nonlinear data, isometric mapping (ISOMAP) is combined with MPS to address the above issues. A method using MPS and ISOMAP for the reconstruction of spatial data is proposed for the accurate reconstruction of unknown spatial data by constructing pattern dataset, dimensionality reduction of patterns, classification of patterns and extraction of patterns, which has provided a new idea for dealing with nonlinear spatial data by MPS. The experimental results show that the structural characteristics of reconstructed results using this method are similar to those of training images.

training image; multiple-point statistics (MPS); pattern; isometric mapping (ISOMAP); dimensionality reduction

2015-05-21；

2015-12-22

中国科学院战略性先导科技专项课题(XDB10030402);中国石油与中国科学院重大战略合作项目(2015A-4812);国家自然科学基金项目(41672114);上海市自然科学基金项目(16ZR1413200);上海第二工业大学校级重点学科建设计算机科学与技术项目(XXKZD1604) This work was supported by the State Priority Research Program of the Chinese Academy of Sciences (XDB10030402), CNPC-CAS Strategic Cooperation Research Program (2015A-4812), the National Natural Science Foundation of China (41672114), the Natural Science Foundation of Shanghai (16ZR1413200), and the Key Discipline of Computer Science and Technology of Shanghai Polytechnic University (XXKZD1604).

张挺(tingzh@shiep.edu.cn)

TP391.41