既有钢筋混凝土码头保护层锈胀开裂计算时长对比

吴灵杰，寇新建，周拥军，蒋 萌

(上海交通大学 船舶海洋与建筑工程学院，上海200240)



既有钢筋混凝土码头保护层锈胀开裂计算时长对比

吴灵杰，寇新建，周拥军，蒋 萌

(上海交通大学 船舶海洋与建筑工程学院，上海200240)

为评估北部湾某在役混凝土码头的耐久性状态，预测其剩余使用寿命.本文基于现场检测结果，通过确定性预测模型和随机性预测模型，对比分析了该混凝土码头的保护层锈胀开裂时长.结果表明，在确定性预测模型中，根据列举的8种模型计算得到保护层锈胀开裂时长为2.09～22.77 a.对于较为恶劣的氯离子侵蚀环境，学者和工程师给出的经验值2～5 a是合理的.在随机性预测模型中，本文考虑了裂缝宽度限值的随机性以及腐蚀速率时变特性，计算得到保护层锈胀开裂时长约为12.7 a，该值与确定性模型的计算结果相吻合.裂缝宽度限值和腐蚀速率对保护层锈胀开裂时长的预测有着显著影响.当腐蚀速率从0.5 μA/cm2上升到1.0 μA/cm2时，保护层锈胀开裂时长减少了14.75 %；而当裂缝宽度限值从0.15 mm增加到0.5 mm时，保护层锈胀开裂时长则增加了39.13 %.研究显示被检测混凝土码头能很好地满足设计使用年限要求.关键词: 混凝土；氯离子；腐蚀发展；随机性模型；确定性模型

众所周知，根据经典的Tuutti模型，对于含氯环境中的钢筋混凝土，钢筋的腐蚀过程可分为两个阶段[1].第一阶段，即所谓的腐蚀初始阶段ti，在氯离子渗入的情况下，但钢筋仍然处于钝化状态，当钢筋表面氯离子质量分数累积达到阀值，致使钢筋脱钝，即意味着腐蚀初始阶段的终结；第二阶段就是所谓的腐蚀发展阶段tp，由于氯离子的活化，促使钢筋不断腐蚀，截面积随时间减少，导致结构承载能力随之下降.

近年来，由于混凝土中钢筋腐蚀的现象越发严重，学者们提出了数种不同的模型用于描述混凝土中钢筋的劣化程度.这模型集中于腐蚀初始阶段，腐蚀发展阶段的预测模型则相对较少[2].然而，忽略腐蚀发展阶段对于暴露在腐蚀环境下的结构进行耐久性评估显然是不合理的[2].

由于混凝土保护层开裂导致钢筋混凝土耐久性失效，学者们做了不少工作，并提出了数种预测模型[2-12].Zhang等[3]提出了一个裂缝宽度随侵蚀深度呈线性增长的预测模型，随后该模型被DuraCrete 2000采用.Vu等[4]基于试验研究结果，提出了一个裂缝宽度与混凝土质量(保护层厚度和水灰比)相互关联的非线性模型.然而，上述模型没有考虑荷载情况对裂缝发展的影响.根据受荷状态下钢筋混凝土梁的试验数据，Vidal等[5]提出了一个裂缝发展和钢筋截面损失线性相关的预测模型.此外，Liang等[2]还对部分预测模型进行了对比分析，然而该研究仅针对确定性模型，并未考虑随机性模型.

本文通过对北部湾某码头的现场检测，预测了混凝土码头的钢筋腐蚀开裂耐久性寿命.由于钢筋腐蚀的复杂性，基于确定性模型和随机模型，对比分析被检测钢筋混凝土码头的腐蚀发展阶段时长tp.在确定性模型中，tp定义为混凝土中钢筋腐蚀至劣化程度为0.8的时间[2]；在随机性模型中，tp则定义为保护层裂缝宽度到达某一限值的时间.此外，在随机模型中，本文还考虑了裂缝宽度限值wcr的随机特性和腐蚀速率icorr的时变特性.

1 计算模型介绍

1.1 确定性预测模型

1.1.1 Bazant模型

由氯离子侵蚀引起的钢筋腐蚀，其腐蚀产物会造成钢筋膨胀，使得混凝土内部产生应力变化，Bazant[6]根据弹塑性分析，得到应力Pr和径向变形Δφ(0)的关系：

(1)

式中：φ(0)为钢筋直径，δpp为钢筋孔洞的径向柔度，ft为混凝土抗拉强度，d为保护层厚度.

钢筋孔洞的径向柔度为

(2)

式中：Eef为混凝土有效弹性模量，Eef=Ec/(1+φp)，Ec为混凝土弹性模量，φp为蠕变系数，vc为混凝土泊松比，S为钢筋间距.

最终，Bazant模型求解tp如下：

(3)

式中：ρp为稳定腐蚀阶段钢筋的平均密度，jr为腐蚀物生成速率.

1.1.2 CW模型

对于普通钢筋混凝土结构，Candy等[7]指出其腐蚀发展阶段的持续时间约为2～5 a.本文取其平均值，即tp=3.5 a.

1.1.3 LW模型

Liu等[8]指出钢筋的腐蚀产物并非是呈线性增长的，不同的腐蚀产物，对于腐蚀胀裂时间会有一定程度的影响.因此，腐蚀产物的多寡是计算tp的重要因素.

临界腐蚀物产量Wcrit可表述为

(4)

式中：d0为混凝土孔隙厚度；a为假想混凝土薄管的内径，(φ(0)+2d0)/2；b为假想混凝土薄管的外径，d+(φ(0)+2d0)/2；ρst为钢筋密度；Wst为锈蚀钢筋质量.

由于扩散与腐蚀产物厚度成反比关系，即

(5)

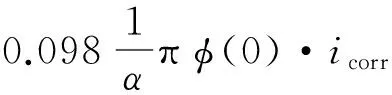
整理得[8]

(6)

1.1.4 ME模型

Mangat[9]等基于室内加速腐蚀试验，针对不同腐蚀状态模拟钢筋腐蚀情况，并提出了tp的预测模型.

腐蚀电流和材料失重之间的关系通常表示为

(7)

式中：ΔW为材料因腐蚀所造成的失重，A为铁的原子量，I为腐蚀电流，t为时间，F为法拉第常数，Z为亚铁离子价数.

则材料损失厚度δ为

(8)

整理得到[9]

(9)

式中ρst为钢筋密度.

1.1.5 VS模型

Vu等[10]提出了腐蚀速率icorr的预测模型，根据该模型进行反推，即可得到tp的预测模型：

(10)

1.1.6 Liang模型

Liang等[2]对Bazant模型进行了修正.依据力学平衡，当混凝土开裂时，将钢筋直径增量Δφ(0)修改为Δφ(0)′:

(11)

最终，修正后的tp计算公式为[9]

(12)

1.1.7 Lounis模型和Andrade模型

Lounis等[11]将钢筋混凝土结构假想为一个厚壁圆筒，钢筋腐蚀膨胀，导致内部产生一个环向的均匀压力Pi，则钢筋的直径变化Δφ(0)可表示为

(13)

而tp的计算公式为[11]

(14)

此外，根据试验结果，Andrade等[12]指出，钢筋的直径变化Δφ(0)可表示为

(15)

因此，整理得，tp又可表示为

(16)

1.2 随机性预测模型

基于随机性模型预测钢筋混凝土结构的腐蚀发展阶段持续时间，首要任务便是确定结构的极限状态.正常使用极限状态SLS下，极限状态方程可由裂缝宽度到达某一限值来表述[1].根据本文被检测码头的实际情况，长期处于受荷状态，因此，选择Vidal等[5]提出的保护层锈胀开裂预测模型将会更加合理.

由氯离子侵蚀引起的混凝土保护层开裂问题，抗力为wcr，作用效应则为w(t)，极限状态方程Z为

(17)

根据Vidal模型，裂缝宽度w(t)和钢筋截面损失的关系为

(18)

式中：ΔA(t)为钢筋截面损失，ΔAs0表示为

(19)

式中：As为钢筋初始截面积；φ(0)为钢筋初始直径；R是和钢筋腐蚀类型相关的一个常数，氯离子侵蚀环境下，通常认为钢筋腐蚀类型为点蚀或者坑蚀[1].

由氯离子侵蚀引起的钢筋直径损失φ(t)则可表示为[13]

(20)

式中：λ=0.011 6Ricorr，ti为钢筋初锈时间，icorr由于其时变特性，采用Vu 等[10]的计算模型，如式(21)所示.

(21)

因此，ΔA(t) 可表示为

(22)

2 被检测码头情况描述

广西省北部湾防城港区13#泊位码头为7万t级散货码头，建成于2005年11月.码头水灰比为0.40，混凝土配合见表1.检测时间为2012年7月下旬，至此，被检测码头已经服役80个月.

表1 码头外墙混凝土配合比

现场检测采用钻孔取样法研究氯离子侵蚀，采用RCT测试仪测定混凝土试样中氯离子的质量分数.混凝土保护层厚度的检测采用Profometer5钢筋保护层测试仪，混凝土码头强度检测采用回弹法.

根据被检测码头实际情况[14]以及文献资料[2]，对于确定性模型，具体计算参数如下：钢筋直径φ(0)=0.022 m，保护层厚度d=59.5 mm，混凝土抗力强度ft=1.7 MPa，混凝土弹性模量Ec=32.5 GPa，蠕变系数φp=2.0，泊松比vc=0.18，钢筋间距S=0.1 m，稳定腐蚀阶段钢筋的平均密度ρp=3.6 g/cm3，腐蚀物生成速率jr=1.5×10-15g·m-2·s-1，混凝土孔隙厚度d0=12.5×10-3mm，α=0.573，钢筋密度ρst=7.86 g/m3，铁的原子量A=56，亚铁离子(Fe2+)价数Z=2，法拉第常数F=0.003 1 A·a，材料损失的厚度δ=0.05 mm.其中，关键参数腐蚀速率icorr本文将依次选用0.1、0.2直到1.0 μA/cm2这10组数据.

基于随机可靠度方法预测钢筋腐蚀发展阶段时长，文献中对系数R推荐值比较统一，根据Stewart等[13]的建议，本文取系数R服从正态分布，均值为3.0，变异系数为0.33.对于裂缝宽度限值wcr，文献以及混凝土规范中给出的推荐值通常在0.15～0.50 mm[1].本文较保守地选择裂缝宽度限值wcr服从均匀分布[14]，最大值为0.30 mm，最小值为0.15 mm.

3 结果与讨论

3.1 基于确定性方法的腐蚀发展阶段时长

将上述参数代入1.1节所列举的计算模型中，即可得到基于确定性模型的腐蚀发展阶段时长tp，计算结果见表2.

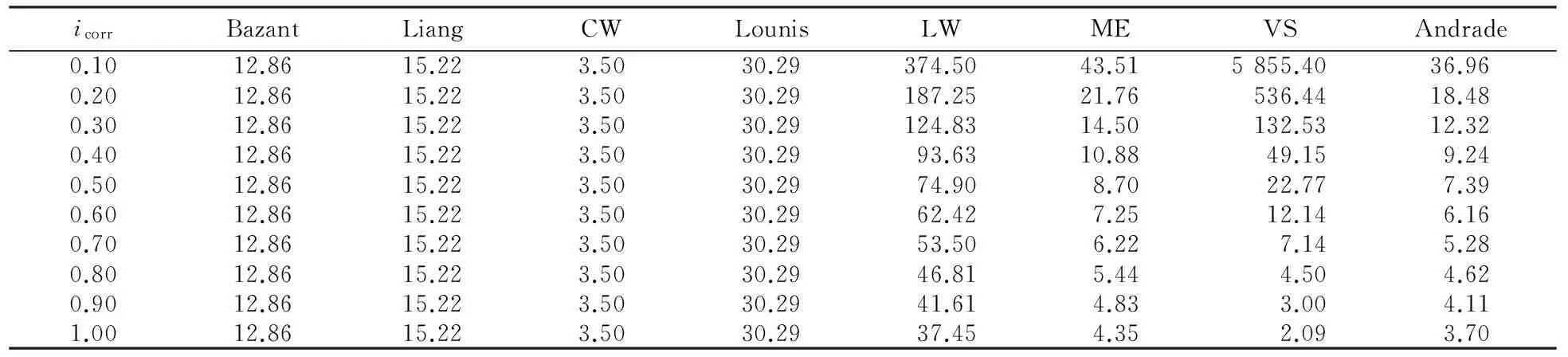
表2 基于确定性模型的腐蚀发展阶段时长

在表2中，Bazant、Liang和Lounis模型均没有考虑锈蚀速率icorr的时变特性对tp计算结果的影响，且Lounis模型较其它模型结果明显偏大，高估了腐蚀发展阶段的时长.Liang等[15]指出，tp的大小应该为钢筋初锈时间ti的1/4～1/5.而文献[14]基于蒙特卡罗模拟方法计算得到该混凝土码头ti约为40 a.如果Liang的观点正确，那么显然Bazant模型计算结果是最合理的.CW模型只是给出了一个经验值2～5 a，没有考虑环境因素的影响，该值虽然较为保守，却为众多学者所接受[1-2].

LW、ME、VS和Andrade模型均考虑了腐蚀速率icorr的时变特性.LW模型计算过程复杂，并不适合在实际工程中的应用，且结果较其余3种模型偏大.VS模型对腐蚀速率icorr表现出了较大的敏感性，当腐蚀速率icorr提高10倍，即从0.10提高到1.00 μA/cm2，相应的tp数值从5 855.40 a下降到了2.09 a，下降了近2 800倍.被检测混凝土码头长期处于受荷状态，侵蚀环境极为复杂且恶劣，因此，腐蚀速率icorr的取值应大于0.50 μA/cm2.从表2可知，当腐蚀速率icorr=0.50 μA/cm2，根据Liang等[15]的理论，ME和Andrade模型的计算结果十分合理；而当腐蚀速率icorr取值为0.60～0.70 μA/cm2时，VS模型的计算结果较好地吻合Liang的理论.此外，当icorr≥0.70 μA/cm2时，ME、VS和Andrade模型计算得到tp数值十分接近，最大值为7.14 a，最小值为2.09 a，这与CW模型推荐的经验值2～5 a近似，这也从另一个角度解释了CW模型广为接受的原因.表2给出的8种预测模型，Lounis和LW模型理论上较为详细，考虑的因素较多，但计算结果却不尽理想，可能是这两个方法针对性较强，模型中部分经验系数并不适合本文的被检测码头所致.

根据上述讨论结果，基于确定性模型预测得到tp数值应在2.09～22.77 a.

3.2 基于随机性方法的腐蚀发展阶段时长

上述讨论皆是基于确定性预测模型，图1给出了基于随机性预测模型的结构时变可靠度指标.

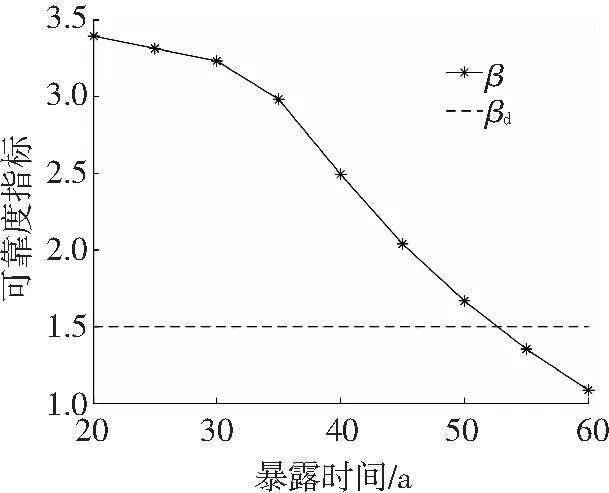
图1 时变可靠度指标

对于设计使用年限为50 a的普通钢筋混凝土结构，正常使用极限状态下，规范中给出的目标可靠度指标βd通常为1.5[1].由图1可知，基于随机性预测模型，被检测钢筋混凝土码头的使用寿命为52.7 a，很好满足了设计使用年限的要求.已知该混凝土码头的钢筋初锈时间ti约为40 a[14]，依此，腐蚀发展阶段的时长tp=12.7 a，与上文Bazant(确定性)模型计算得到的12.86 a相近.进一步计算可知tp约为ti的31.25 %，近似于Liang等[15]所推荐的25 %.此外，Val等[16]给出了一种简化的腐蚀发展阶段的时长tp判定办法，tp的大小约为10倍的混凝土初始裂缝形成所需的时间.而试验研究显示，混凝土初始裂缝形成的时间往往在200～400 d[17].基于此，相应的tp值应为5.5～11.0 a，同样与本文的结果接近.综上所述，本文计算得到腐蚀发展阶段的时长tp=12.7 a是可信的.

混凝土规范中给出的混凝土裂缝宽度限值通常在0.15～0.30 mm，而文献[1-2]中，给出的却通常在0.30～0.50 mm.图2、3分别给出了不同裂缝宽度限值wcr和腐蚀速率icorr下的时变可靠度.

图2 不同裂缝宽度限值下时变可靠度指标

Fig.2 Time-dependent reliability index with various limit crack widths

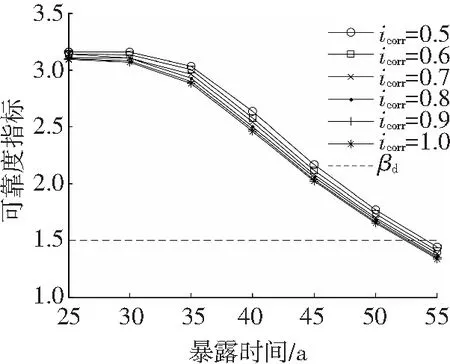
图3 不同腐蚀速率下时变可靠度指标

由图2和图3可知，增加裂缝宽度限值wcr会使相应的结构使用寿命增加，与此相反，结构使用寿命会随腐蚀速率icorr的增大而减小.在给定目标可靠度指标βd=1.5的情况下，当裂缝宽度限值wcr=0.15、0.2、0.3、0.4和0.5 mm时，相应的使用寿命分别为51.5、52.2、53.5、54.5和56 a；当腐蚀速率icorr为0.5、0.6、0.7、0.8、0.9和0.5 μA/cm2时，相应的使用寿命分别为54、53.5、53、52.6、52.3和52.2 a.改变裂缝宽度限值wcr和腐蚀速率icorr的数值看似对结构使用寿命的影响并不明显，这是因为腐蚀发展阶段的时长在结构使用寿命中所占比例较小.如果仅仅考虑腐蚀发展阶段的时长tp，从图2可知，当裂缝宽度限值wcr从0.15 mm提高到0.5 mm，tp增加了39.13 %；从图3可知，当腐蚀速率icorr从0.5μA/cm2增加到1.0 μA/cm2，tp减少了14.75 %.

4 结 论

1)基于确定性模型，根据列举的8种方法，钢筋腐蚀发展阶段时长tp为2.09～22.77 a.对于较恶劣的侵蚀环境，Candy和Weyers推荐的tp经验值2～5 a是合理的.

2)根据随机性模型，在给定目标可靠度指标βd=1.5情况下，得到腐蚀发展阶段时长tp=12.7 a，该结果与Bazant(确定性)模型的计算值12.86 a近似.被检测钢筋混凝土码头能满足设计使用年限的要求.

3)裂缝宽度限值wcr和腐蚀速率icorr对腐蚀发展阶段时长tp的计算结果有着显著影响.当wcr从0.15 mm增加到0.5 mm时，tp增加了39.13 %；而当icorr从0.5 μA/cm2增加到1.0 μA/cm2时，tp减少了14.75 %.

[1] SHI X M, XIE N, FORTUNE K, et al. Durability of steel reinforced concrete in chloride environments: An overview [J]. Construction and Building Materials, 2012, 30: 125-138. DOI: 10.1016/j.conbuildmat.2011.12.038.

[2] LIANG M, LIN L, LIANG C. Service life prediction of existing reinforced concrete bridges exposed to chloride environment [J]. Journal of Infrastructure Systems, 2002, 8(3): 76-85. DOI: 10.1061/(ASCE)1076-0342(2002)8:3(76).

[3] ZHANG R J, CASTEL A, FRANCOIS R. Concrete cover cracking with reinforcement corrosion of RC beam during chloride-induced corrosion process[J]. Cement and Concrete Research, 2010, 40(3): 415-425. DOI: 10.1016/j.cemconres.2009.09.026.

[4] VU K, STEWART M G, MULLARD J. Corrosion-induced cracking: Experimental data and predictive models [J]. ACI Structural Journal, 2005, 102(5): 719-726.

[5] VIDAL T, CASTEL A, FRANCOIS R. Analyzing crack width to predict corrosion in reinforced concrete [J]. Cement and Concrete Research, 2004, 34(1): 165-174. DOI: 10.1016/S0008-8846(03)00246-1.

[6] BAZANT Z P. Physical model for steel corrosion inconcrete sea structures-theory [J]. Journal of the Structural Division, 1979, 105(6): 1137-1153.

[7] CADY P, WEYERS R. Deterioration rates ofconcrete bridge decks [J]. Journal of Transportation Engineering, 1984, 110(1): 34-44. DOI: 10.1061/(ASCE)0733-947X(1984)110:1(34).

[8] LIU Y, WEYERS R E. Modeling the time-to-corrosion cracking in chloride contaminated reinforced concrete structures [J]. ACI Materials Journal, 1998, 95(6): 675-681.

[9] MANGAT P S, ELGARF M S. Flexural strength of concrete beams with corroding reinforcement [J]. ACI Materials Journal, 1999, 96(1): 149-158.

[10]VU K A T, STEWART M G. Structural reliability of concrete bridges including improved chloride-induced corrosion models [J]. Structural Safety, 2000, 22(4): 313-333. DOI: 10.1016/S0167-4730(00)00018-7.

[11]LOUNIS Z, DAIGLE L. Reliability-based decision support tool for life cycle design and management of highway bridge decks: 20378143 [R].Ontario: National Research Council Canada, 2008.

[12]ANDRADE C, ALONSO C. On-site measurements of corrosion rate of reinforcements [J]. Construction and Building Materials, 2001, 15(2-3): 141-145. DOI: 10.1016/S0950-0618(00)00063-5.

[13]STEWART M G, ROSOWSKY D V. Time-dependent reliability of deteriorating reinforced concrete bridge decks [J]. Structural Safety, 1998, 20(1): 91-109. DOI: 10.1016/S0167-4730(97)00021-0.

[14]WU L J, KOU X J, JIANG M. Probabilistic Corrosion Initiation Time Assessment of Existing Concrete Structures Under Marine Environment [J]. Arabian Journal for Science and Engineering, 2015, 40(11): 3099-3105. DOI: 10.1007/s13369-015-1774-y.

[15]LIANG M T, WANG K L, LIANG C H. Service life prediction of reinforced concrete structures [J]. Cement and Concrete Research, 1999, 29(9): 1411-1418. DOI: 10.1016/S0008-8846(99)00109-X.

[16]VAL D V, STEWART M G. Life-cycle cost analysis of reinforced concrete structures in marine environments [J]. Structural Safety, 2003, 25(4): 343-362. DOI: 10.1016/S0167-4730(03)00014-6.

[17]KHAN I, FRANCOIS R, CASTEL A. Prediction of reinforcement corrosion using corrosion induced cracks width in corroded reinforced concrete beams [J]. Cement and Concrete Research, 2014, 56: 84-96. DOI: 10.1016/j.cemconres.2013.11.006.

(编辑 赵丽莹)

Propagation assessment of existing concrete dock based on concrete cover corrosion-crack

WU Lingjie, KOU Xinjian, ZHOU Yongjun, JIANG Meng

(School of Naval Architecture, Ocean and Civil Engineering,Shanghai Jiaotong University, Shanghai 200240, China)

To assess the durability status and remaining service life of existing concrete dock located at Beibu Gulf, the propagation phase was evaluated based on the in situ test data and concrete cover corrosion-crack model. The results indicate that the propagation phase will last about 2.09-22.77 years based on eight deterministic models. The empirical values of 2-5 years, recommended by scholars and engineers, would be more reasonable when the RC structures were exposed to harsh corrosion environment. According to the probabilistic model, the uncertainty of limit crack width and time-dependent characteristic of the corrosion rate were taken into considered, the propagation phase equated to 12.7 years, which was fitted with the deterministic models. The limit crack width and corrosion rate significantly affect the assessment of the propagation phase. When the value of corrosion rate increases from 0.5 to 1.0 μA/cm2, the value of the propagation phase decreases by 14.75 %; and the value of the propagation phase increases by 39.13 % when the value of limit crack width rises from 0.15 to 0.50 mm. The study shows that the tested concrete dock can meet the requirement of design service life.

concrete; chloride; propagation phase; probabilistic model; deterministic model

10.11918/j.issn.0367-6234.2016.12.006

2015-11-30

国家自然科学基金(41274012)

吴灵杰 (1988—)，男，博士研究生; 寇新建 (1950—)，男，教授，博士导师

吴灵杰，79186643@sjtu.edu.cn

TU528.0

A

0367-6234(2016)12-0051-05