基于TD-RLS算法的四旋翼飞行器系统参数辨识

万慧, 齐晓慧

(军械工程学院 无人机工程系, 河北 石家庄 050003)



基于TD-RLS算法的四旋翼飞行器系统参数辨识

万慧, 齐晓慧

(军械工程学院 无人机工程系, 河北 石家庄 050003)

在对飞行器气动参数进行辨识的过程中,常需要对获得的数据求微分或二次微分,而利用差分法求微分会放大噪声的影响,引入滤波器抑制噪声又会产生相位延迟。针对这一问题,提出了一种跟踪微分器-递推最小二乘(TD-RLS)辨识算法。首先,建立了悬停条件下四旋翼飞行器的系统模型;然后,基于实验室四旋翼平台飞行试验实测数据,将TD-RLS算法应用于飞行器参数辨识。最终的辨识结果表明,在四旋翼飞行器悬停或者小角度飞行条件下,该方法可以实时获得比较精确的系统模型。

跟踪微分器; 相位延迟; 系统辨识; 四旋翼飞行器

0 引言

四旋翼飞行器具有结构简单、可垂直起降和空中悬停等优点，具有广阔的发展前景[1]。系统模型是四旋翼飞行器控制律设计的基础,准确获得系统模型参数是建立系统模型的关键[2]。随着四旋翼飞行器故障诊断和容错控制的发展,对系统模型参数的实时性和准确性提出了更高的要求[3]。

系统辨识法可利用实际飞行试验中获得的数据,经过适当处理估计出系统参数的值,具有实验成本低、周期短的优点,已成为一种四旋翼飞行器建立准确系统模型的有效手段[4]。

近年来,许多学者对四旋翼飞行器的系统辨识方法进行了研究,取得了一定的成果。刘亮等[5]通过极大似然法对飞行器控制函数的参数进行辨识,得到了较好的结果。宋彦国等[6]采用子空间法与频域加权预报误差法相结合的两步辨识法,得到的辨识结果与理论分析结果具有一致性。陈农等[7]应用自适应小波神经网络对系统参数辨识,避开了复杂的数据建模过程。然而,极大似然法和子空间辨识方法计算复杂程度高,神经网络容易陷入局部最优解,且辨识的实时性较差。应用于实时在线辨识的系统辨识方法主要有递推最小二乘方法(Recursive Least Square,RLS)[8]和卡尔曼滤波方法等,而卡尔曼滤波对初值比较敏感,初值选择不当可能导致估计发散,并不适宜进行参数估计[9]。另外,对四旋翼飞行器参数进行辨识的过程中,常需要对获得的数据进行微分或二次微分,跟踪微分器(Tracking Differentiator,TD)可以合理地从不连续或带有随机噪声的信号中提取连续信号和微分信号,同时具有较好的滤波性能[10]。

本文提出了一种跟踪微分器-递推最小二乘(TD-RLS)辨识算法。首先建立悬停条件下四旋翼飞行器的系统模型;然后设计了TD-RLS算法,利用实验室四旋翼平台飞行试验实测数据,对飞行器参数进行了辨识。

1 四旋翼飞行器动力学模型的建立

如图1所示,为建立四旋翼飞行器动力学模型,首先建立地面坐标系和机体坐标系。定义:地面坐标系原点O为飞行器在地面上的起飞点,x轴为飞行器前进方向,z轴垂直于水平面(向上为正方向),y轴垂直于Oxz平面,与x轴和z轴构成右手系;机体坐标系原点Ob为飞行器的质心,xb轴指向飞行器机头方向,zb轴垂直于飞行器平面(向上为正方向),yb轴垂直于Obxbzb平面,与xb轴和zb轴构成右手系。Fi(i=1,2,3,4)为单个旋翼产生的力。

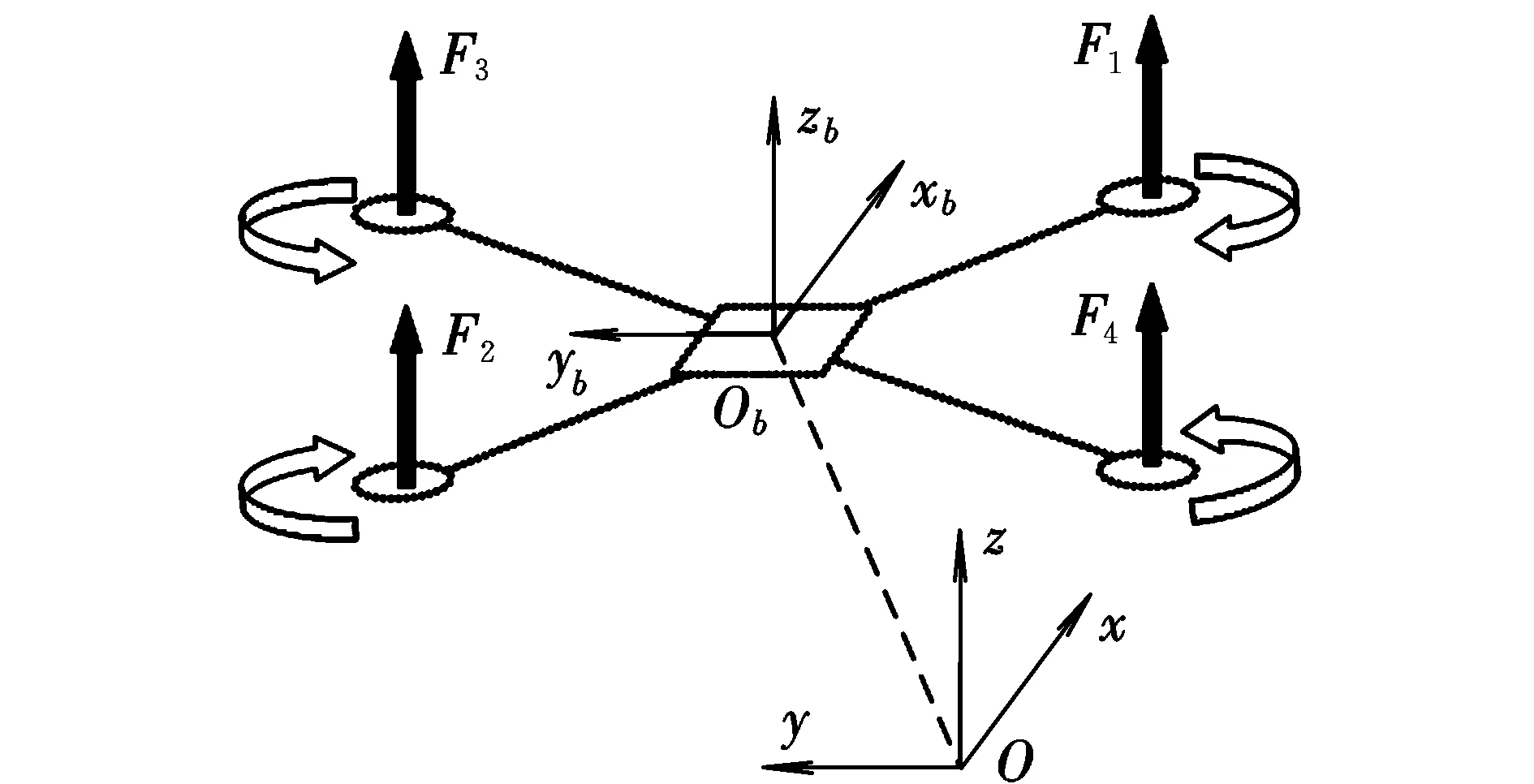
图1 坐标系的建立Fig.1 Establishment of coordinate system

本文主要对处于悬停或小角度飞行状态下的四旋翼飞行器系统参数进行辨识。此时,飞行器低速飞行,三轴角速度较小,忽略水平面上的位移和空气阻力的影响,则四旋翼飞行器的动力学模型可简化为:

(1)

式中:z为飞行器相对地面坐标系垂直方向上的位置;φ,θ,ψ分别为飞行器的滚转角、俯仰角和偏航角;m为飞行器质量;l为飞行器质心到旋翼质心的长度;Ix,Iy,Iz分别为飞行器在机体坐标系3个轴向上的转动惯量;η为升力与随升力产生的扭转力矩的比例;g为重力加速度;Ui(i=1,2,3,4)为解耦后的飞行器模型4个独立控制通道的输入量,具体可表示为:

(2)

单个旋翼产生的力Fi(i=1,2,3,4)的大小与电机的控制量(飞控板输出的PWM波,记为RCOUi(i=1,2,3,4))的关系可表示为:

(3)

式中:CL为升力系数;u为电源电压;G(s)为电机的传递函数,可近似为一阶惯性环节。根据文献[11],G(s)可表示为:

(4)

2 基于TD-RLS的参数辨识算法

2.1 跟踪微分器的离散形式

根据文献[12],为了补偿由信号经过TD后造成的相位损失,可利用TD给出的微分信号对得到的跟踪信号进行适当的预报修正。为了得到更好的滤波效果,本文采用“先预报、后微分”的方法。此时,二阶跟踪-微分器的离散形式可表示为:

(5)

其中:

fhan[x1(k)-v(k),x2(k),r,h0]=

-rsat[g(k),d]

d=h0r,d0=h0d,y(k)=x1(k)+h0x2(k)

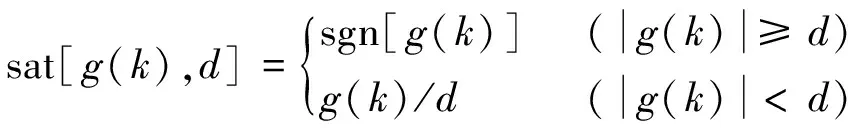
2.2 递推最小二乘算法

2.3 TD-RLS参数辨识算法

根据式(1),四旋翼飞行器在垂直方向上的加速度可表示为:

φcosθm-1-g

(6)

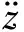
(7)

经整理,变为RLS辨识算法的标准形式:

yn=h(n)CL

(8)

其中:

yn=d(dzn)/(dt)2+g

h(n)=m-1cosφncosθn×

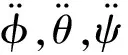
(9)

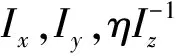
3 应用实例

应用TD-RLS算法对实验室四旋翼平台的参数进行辨识。通过测量,得到m=1.023 kg,l=0.23 m,电源电压u=11.25 V,g取9.8 m/s2。因为所用飞控板电机的控制步长为0.10 s,姿态信息的采样步长为0.02 s,根据式(6)和式(7),需选取同一时刻的姿态信息和控制信息,故取h=0.1,n1=8,n2=16,r=1 000,λ=0.98。辨识过程如下:

(1)对采集的RCOUi(i=1,2,3,4),z,φ,θ,ψ通过TD进行滤波及求微分处理,部分结果如图2和图3所示。

由图2和图3可以看出:四旋翼飞行器采集信息经过TD处理后,跟踪信号较原信号更加平滑;在悬停或者小角度飞行的情况下,得到的数据二次微分也比较符合实际,证明了TD具有较好的滤波和提取微分信号效果。

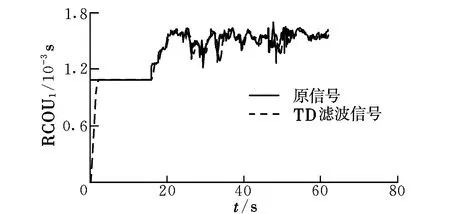
图2 TD对RCOU1滤波Fig.2 Filtering of TD to RCOU1

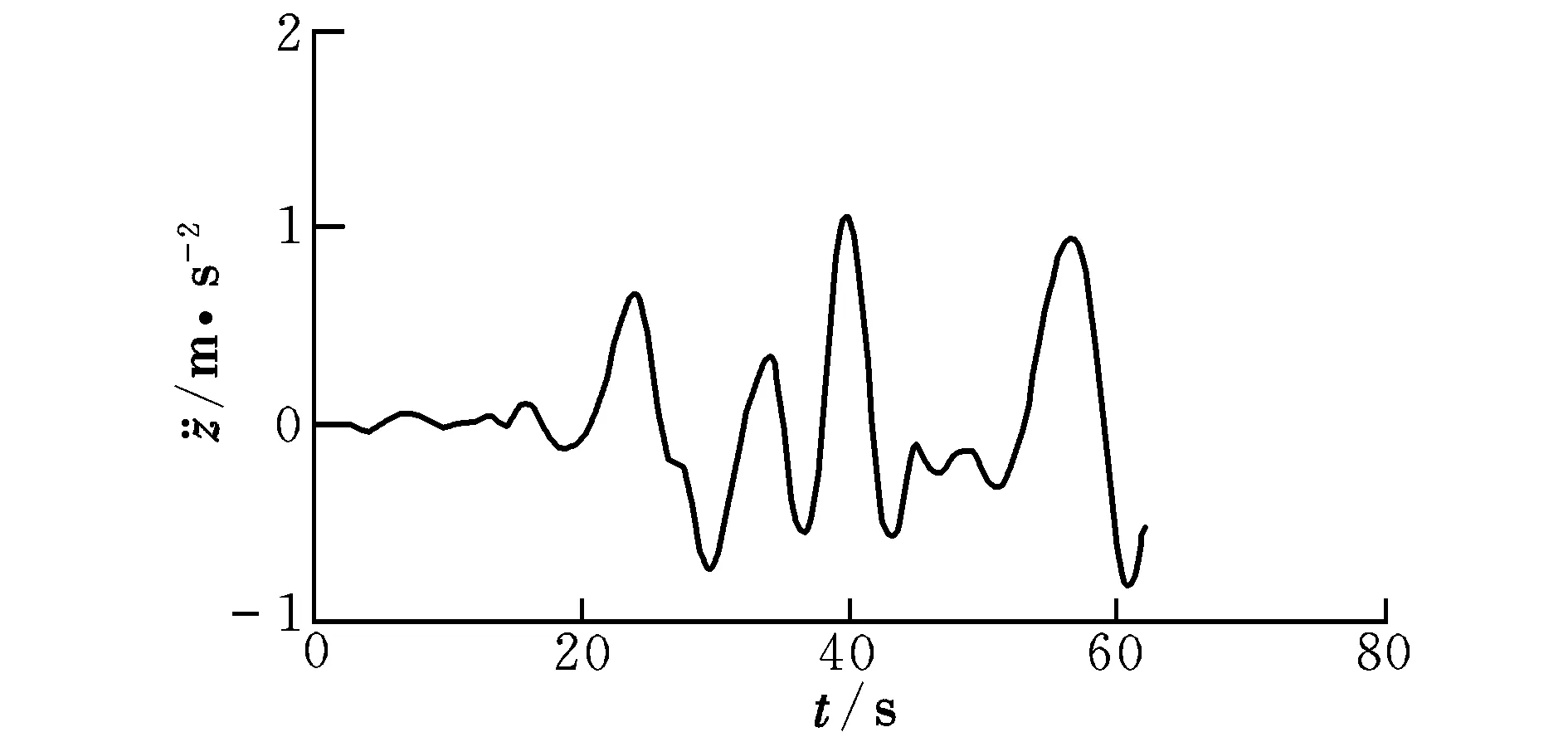
图3 垂直方向加速度Fig.3 Vertical acceleration

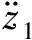
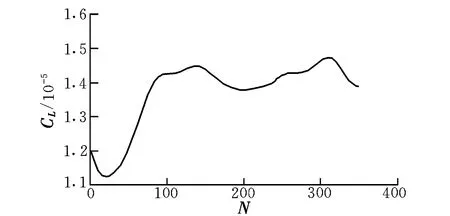
图4 升力系数CL的辨识过程Fig.4 Identification process of CL

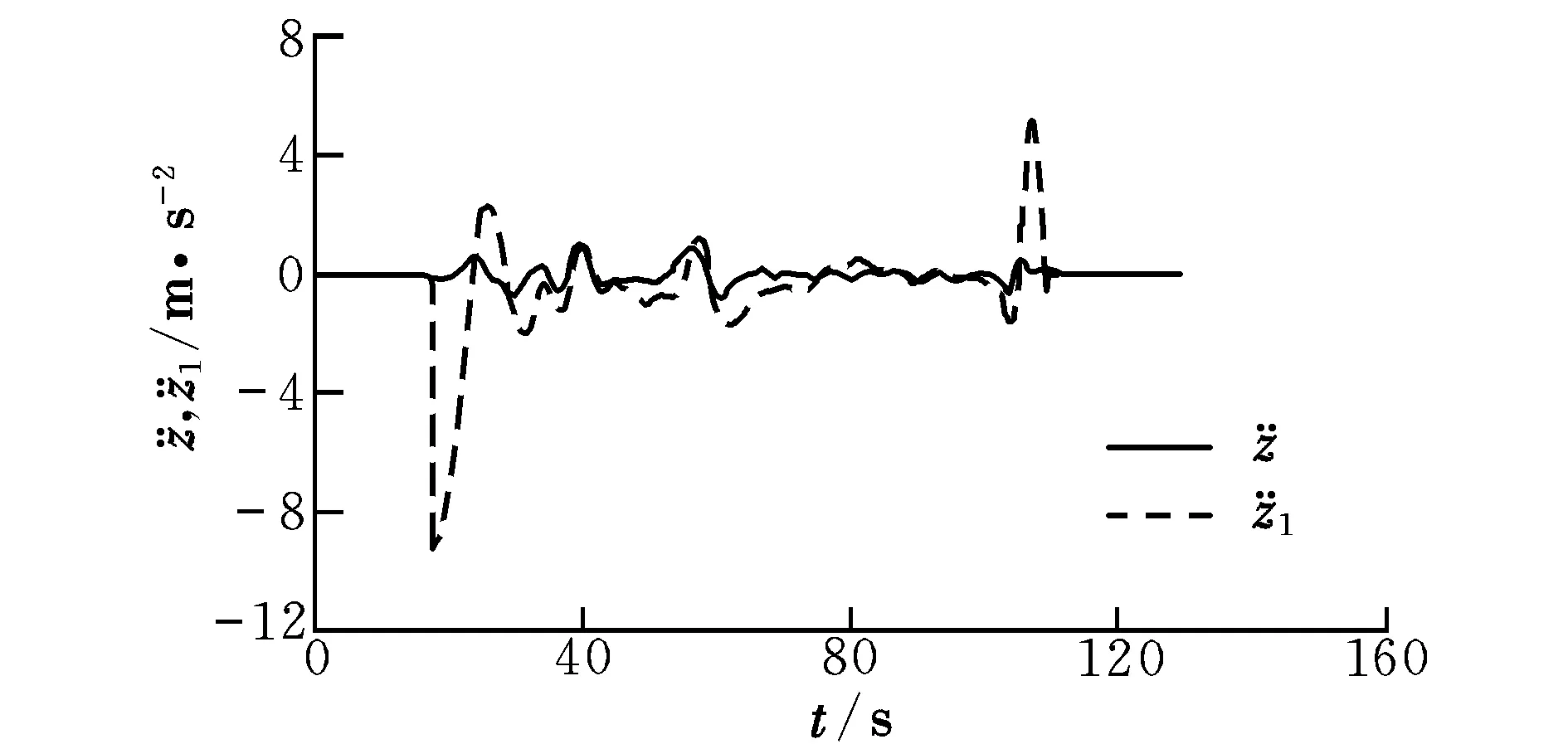
图5 垂直方向加速度Fig.5 Vertical acceleration

由于在飞行器未起飞阶段升力加速度为零,但存在重力加速度,故初始阶段由升力求得的加速度存在负值。

综上可知,由辨识出的CL求得的垂直方向的加速度与实际悬停状态时垂直方向的加速度基本一致,即通过TD-RLS算法辨识出的CL具有较高的可信度。

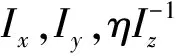
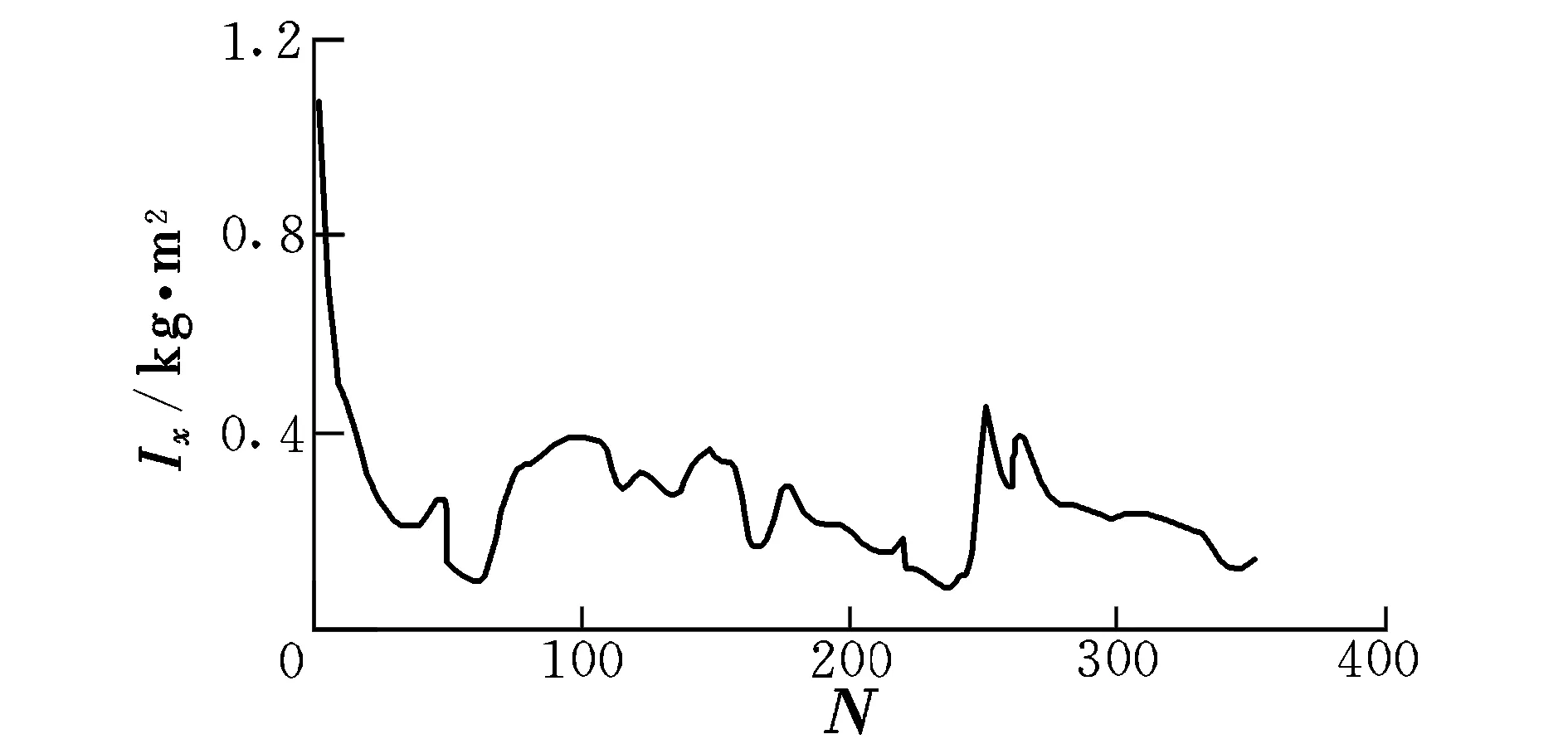
图6 Ix的辨识过程Fig.6 Identification process of Ix

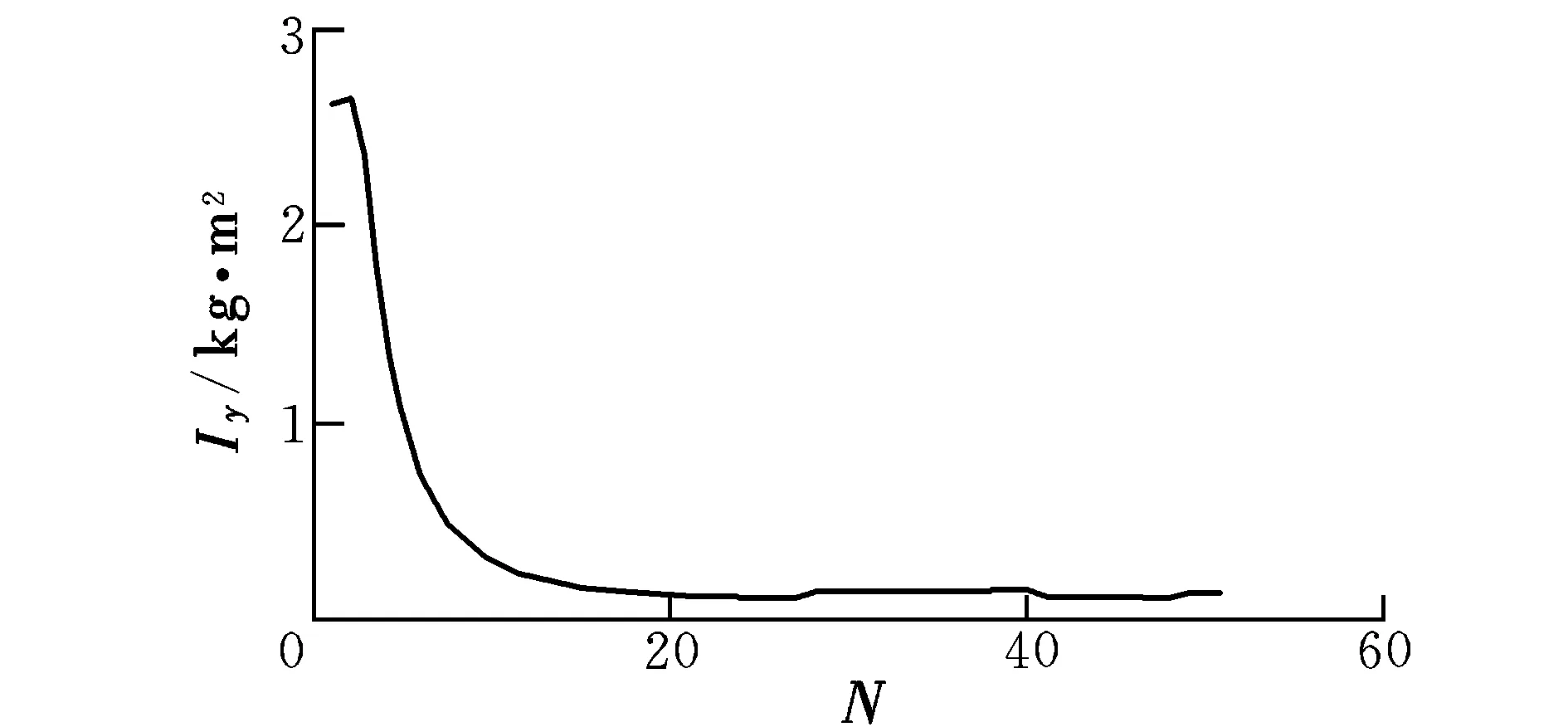
图7 Iy的辨识过程Fig.7 Identification process of Iy

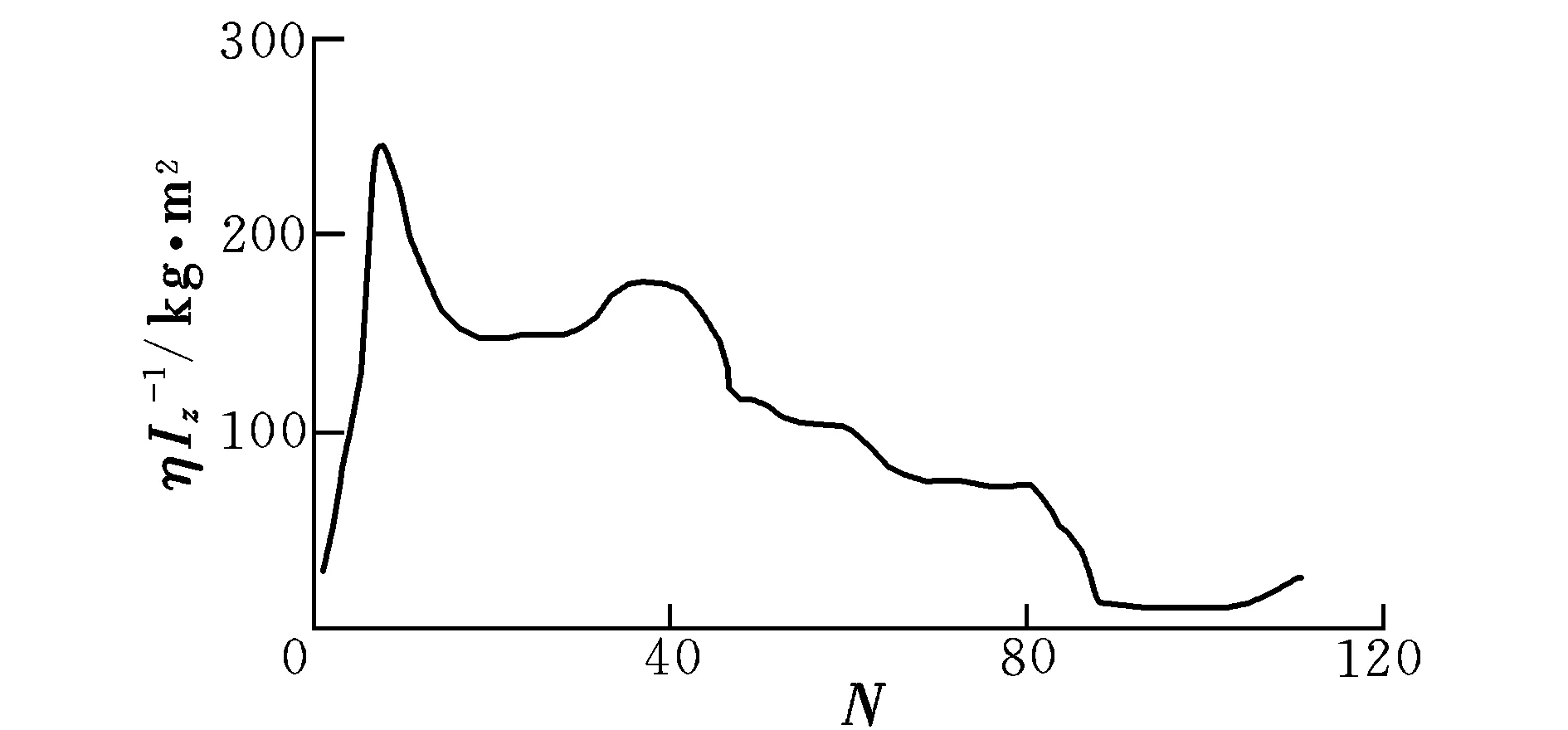
图的辨识过程Fig.

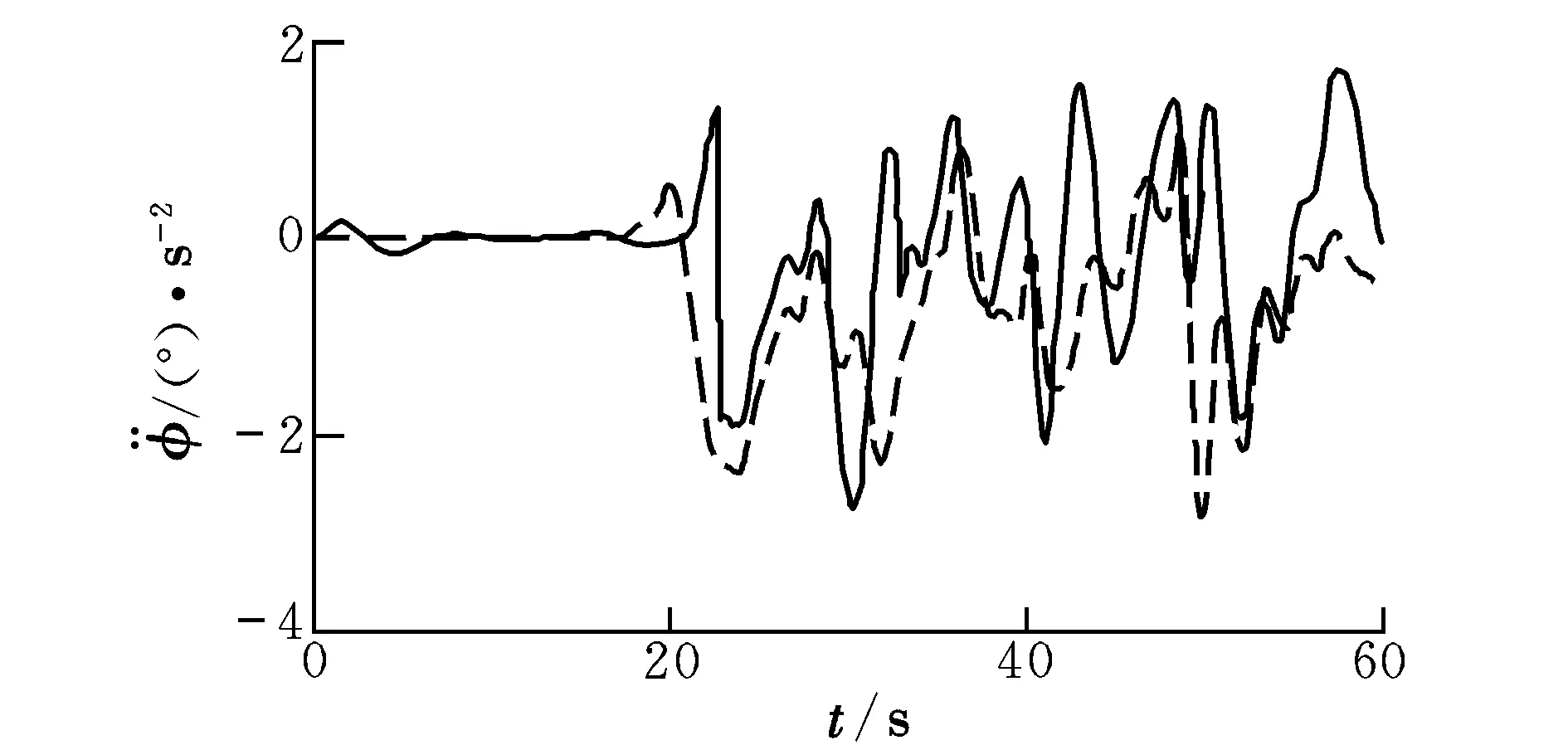
图9 滚转角加速度Fig.9 Acceleration of roll angle

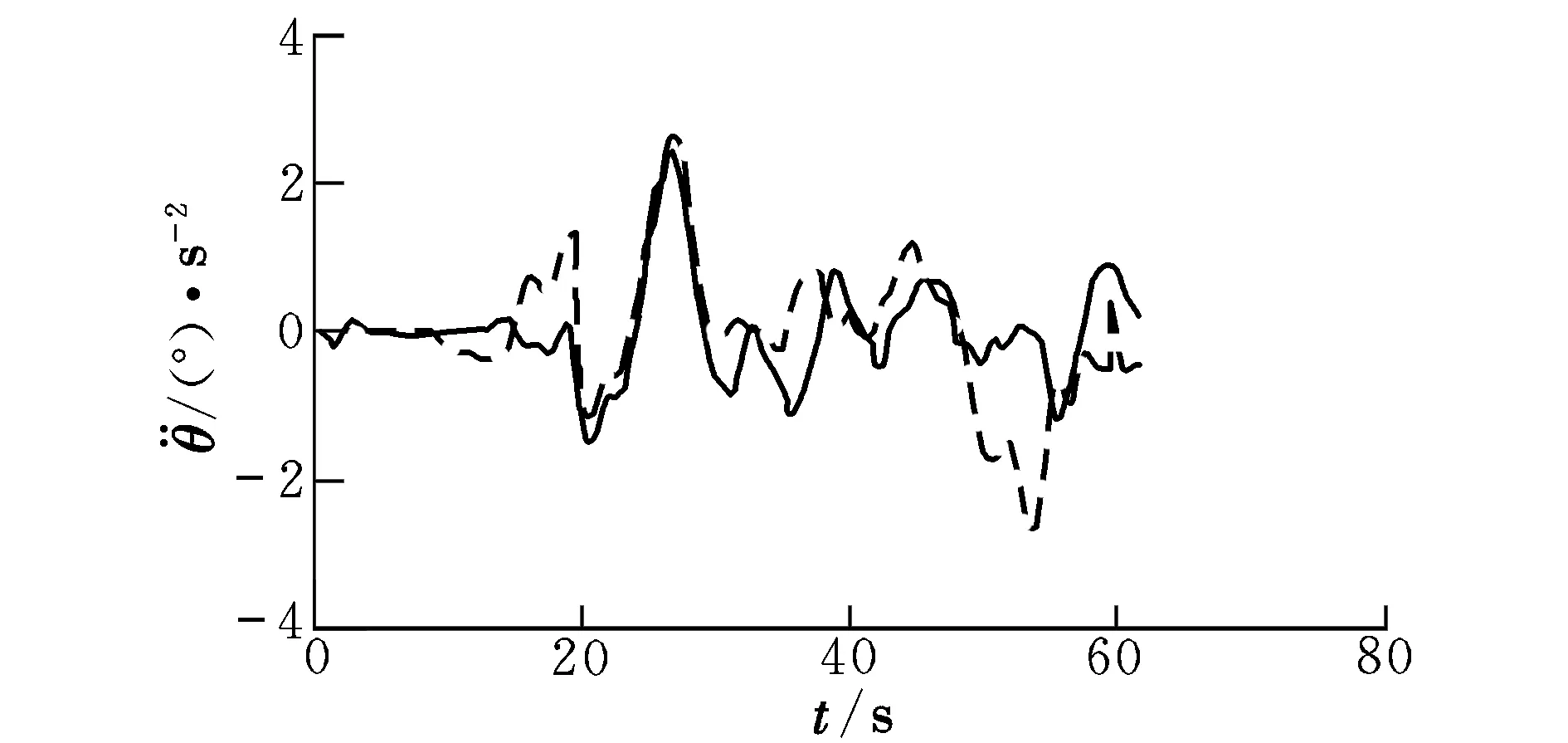
图10 俯仰角加速度Fig.10 Acceleration of pitch angle

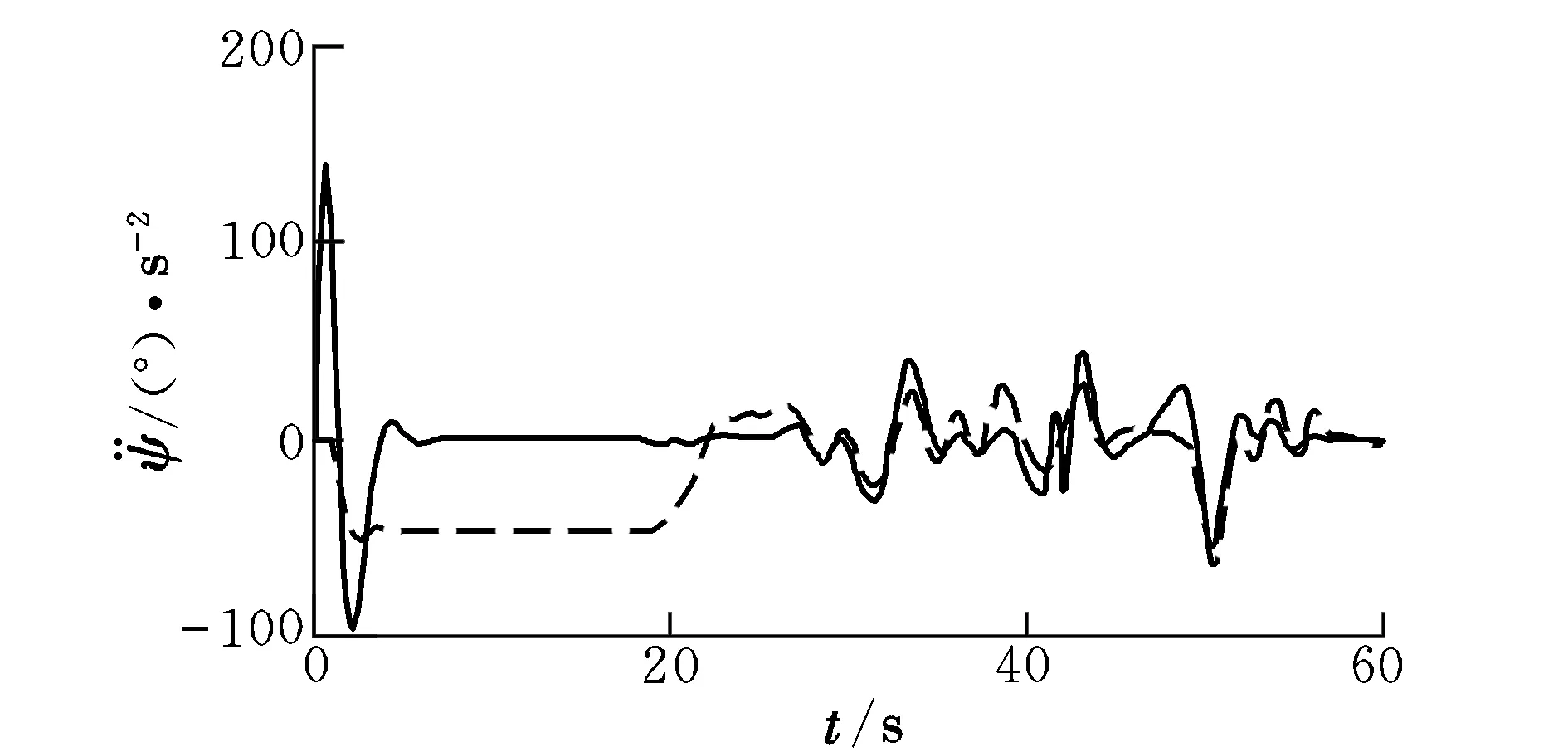
图11 偏航角加速度Fig.11 Acceleration of yaw angle

综上可知,采用TD-RLS算法对四旋翼系统参数进行辨识具有收敛速度较快、辨识精度较高等优势。但由于电机控制延迟、实验人员操作存在偏差等因素,使得实际飞行状态与计算得到的飞行状态还存在一定的偏差。如图11所示,因为四旋翼飞行器未起飞时飞行器实际朝向与设定朝向不符,飞行器起飞后进行了偏航方向的调整,使得实际飞行中的偏航角加速度在初始时存在较大的波动。

4 结束语

本文针对四旋翼系统模型辨识中需要对测量信号求微分和二次微分,且引入滤波器抑制噪声产生相位延迟的问题,提出了一种基于TD-RLS的辨识算法,将微分信号的求解与滤波整合为一个结构,简化了算法。采用该算法对四旋翼飞行器在悬停或者小角度飞行状态下的气动模型相关参数进行了求解,并对所得结果与实际飞行中相关状态进行了验证,结果表明该算法具有较快的收敛速度和较高的收敛精度,在实际工程应用中具有一定的价值。

[1] 甄红涛,齐晓慧,夏明旗,等.四旋翼无人直升机飞行控制技术综述[J].飞行力学,2012,30(4):295-299.

[2] 赵述龙,安宏雷,刘建平,等.四旋翼飞行器模型的气动参数辨识[J].电子测量与仪器学报,2013,27(8):744-748.

[3] 罗峰.自修复飞控系统仿真及重构理论研究[D].西安:西北工业大学,2000.

[4] 李寒冰,吴大卫.一种无人机气动参数辨识的实现方法[J].飞行力学,2014,32(2):183-188.

[5] 刘亮,王林海,张波.超小型旋翼飞行器遥操作仿真模型控制函数的辨识[J].机电工程,2009,26(6):13-16.

[6] 宋彦国,孙涛.旋翼飞行器飞行动力学系统辨识建模算法[J].南京航空航天大学学报,2011,43(3):387-392.

[7] 陈农,贾区耀.用自适应小波神经网络辨识动态实验数据[J].飞行力学,2011,29(1):67-69.

[8] 李响,李为吉.一种实现飞行品质参数实时辨识的实用方法[J].飞行力学,2001,19(2):9-11.

[9] 蔡金狮.飞行器系统辨识学[M].北京:国防工业出版社,2003:55-57.

[10] 李冀鑫,侯志强,郑小洪.离散跟踪微分器在着舰导引滤波中的应用[J].飞行力学,2008,26(4):69-72.

[11] 申珊颖.斜十字四旋翼飞行器实验建模与控制技术研究[D].南京:南京航空航天大学,2013.

[12] 韩京清.自抗扰控制技术[M].北京:国防工业出版社,2013:95-96.

[13] 刘金琨,沈晓蓉,赵龙.系统辨识理论及MATLAB仿真[M].北京:电子工业出版社,2013:41-46.

[14] 齐晓慧,黄健群,董海瑞,等.现代控制理论及应用[M].北京:国防工业出版社,2007:319-320.

(编辑：崔立峰)

Parameter identification of quad-rotor aircraft system based on TD-RLS algorithm

WAN Hui, QI Xiao-hui

(Department of Unmanned Aerial Vehicle Engineering, Ordnance Engineering College, Shijiazhuang 050003,China)

In the parameter identification of aircraft, the obtained data are often used to get differential or quadratic differential.Considering the noise amplification caused by finite difference method for differential and phase delay owing to filter, we proposed a tracking-differentiator and recursive least square (TD-RLS) identification algorithm. Firstly, the system model of a quad-rotor aircraft in hover was built. Then, the algorithm was used for parameter identification of the quad-rotor system based on the measured data of quad-rotor aircraft in our laboratory. The results showed that this method can get accurate system model in hovering or flying with small angle.

tracking-differentiator; phase delay; system identification; quad-rotor aircraft

2016-01-22;

2016-05-04;

时间:2016-05-18 13:49

万慧(1991-)，女，河北秦皇岛人，硕士研究生，研究方向为四旋翼飞行器和自抗扰控制技术。

V212.4; V221.6

A

1002-0853(2016)06-0072-05