压力输水管道管径方程求解法
陈 居 乾
(甘肃省兰州市就业和人才服务局, 甘肃 兰州 730000)
压力输水管道管径方程求解法
陈 居 乾
(甘肃省兰州市就业和人才服务局, 甘肃 兰州 730000)
在各类压力输水工程设计实践中,对于倒虹吸管及一般压力输水管道的管径确定,通常依据复杂多变因素,采用试算法计算选择,由于可变因素较多,计算选择相对繁琐,且工作量较大。本文依据压力管流水力学计算理论,通过分析与方程推导,导出倒虹吸及一般压力输水管道管径,以及直接计算上下游水头与水位差的方程求解法,并分析汇总求解方法及其步骤,计算简便快捷。同时,分别列举工程实例计算予以明确,计算结果准确,可为各类压力输水工程实践提供参考。
倒虹吸管;压力输水管道;管径;水头与水位差;方程求解法
0 前 言
在各类调水、引水及供水等水利工程中,为降低水量损失、减少工程占地、有效保护水质、确保供水压力水头,以及考虑输水线路布置灵活等需要,一般多采用压力管道进行输水。在压力输水水工建筑物不同类型中,倒虹吸为常见与重要的输水建筑物,也是典型的跨沟与穿越地势低洼地段且能保证供水水头的有压输水水工建筑物。通常在工程设计实践中,对于倒虹吸管及一般压力输水管道的设计计算,其流量系数μ与管径d相关联,一般在确定管径时常依据运行水头压力、压坡线、水头损失量、管材价格、经济流速,以及运输与安装施工等复杂多变因素,采用试算法计算选择,由于可变因素较多,计算选择相对繁琐,且工作量较大。依据压力管流水力学计算理论,通过分析与方程推导,导出倒虹吸管径及直接计算运行工作水头的方程求解法,并分析汇总管径方程求解方法及其步骤,管径计算选择简便快捷,工作量大为降低。同时依据倒虹吸管径方程,可延伸应用,进而得出一般压力输水管道不同出流工况的管径,以及直接计算上下游进出口水位差与水头的方程。并分别列举不同类型工程实例进行相应计算,进一步明确管径方程求解方法及其步骤,计算结果准确。
1 倒虹吸管管径方程推导
倒虹吸管水工压力输水建筑物工程一般由进出口上下游水流控制闸室与渐变段、以及中段压力输水管道等组成,其典型布置见图1。

图1 倒虹吸管典型布置示意
从图中可知水面总落差ΔH为:
ΔH=ΔH1+ΔH2+ΔH3
(1)
(2)
(3)
(4)
式中 ΔH1——上游进口闸室水头,m;
ΔH2——进出口之间水头损失量,m;
ΔH3——出口闸室之后渐变段水面回升量,m;
v1——上游渠道断面流速,m/s;
v2——进口上游渐变渠段末端断面流速,m/s;
v——压力输水管道出口断面流速,m/s;
v3——下游渠道断面流速,m/s;
ζ1——进口上游渐变渠段局部水头损失系数;
ζi——压力输水管道某一转弯点等轴线变化处局部水头损失系数;
ζ2——出口下游渐变渠段局部水头损失系数;
λ——压力输水管道沿程水头损失系数;
L——压力输水管道管长,m;
d——压力输水管道净管径,m;
g——重力加速度,取9.81m/s2。
由(3)式及Q=wv可得:
(5)
(6)
(7)
式中Q——输水流量,m3/s;
μ——流量系数;
w——压力输水管道净断面面积,m2。
由(1)、(2)、(4)式得:
(8)
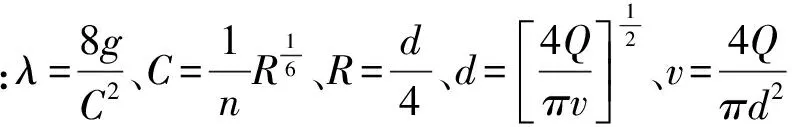
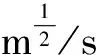
n——压力输水管道水力糙率;
R——压力输水管道净断面水力半径,m。
由(5)、(6)、(8)式可归纳分析计算得:
(9)
为简化繁琐计算式,令:
则(9)式可简化为:
x4-Ax-B=0
(10)
由此,(10)式即为倒虹吸管管径的通用标准方程式,可依据倒虹吸管进出口布置及其型式与结构的不同,分别归纳分析其特定不同结构与布置型式的上下游水位总落差ΔH(运行工作水头),以及关键参数A与B的计算确定方程式。
1.1 进出口设置渐变段
当倒虹吸管进出口设置渐变段,且上下游渠道流量与断面流速相等或近似相同,即v1=v3时,上下游渠道水位总落差ΔH(运行工作水头)(9)式则为:
(11)
由此可得:
(11-1)
(11-2)
1.2 进出口不设渐变段
当倒虹吸管进出口不设置渐变段,且进出口上下游渐变渠段局部水头损失系数,以及上下游渠道流量与断面流速相等或近似相同,即ζ1=ζ2=0、v1=v2=v3时,上下游渠道水位总落差ΔH(运行工作水头)(9)式则为:
(12)
由此可得:
A=0.082 7∑ζiQ2ΔH-1
(12-1)
B=10.293 5Q2n2LΔH-1
(12-2)
2 一般压力输水管道管径方程
当倒虹吸管进出口不设置渐变段,出口自由出流或淹没出流时,即变为自由出流或淹没出流的一般压力输水管道,可由倒虹吸管管径方程得出一般压力输水管道的管径方程,仍为x4-Ax-B=0。可依据压力输水管道出口不同的出流工况,分别归纳分析其特定工况的压力水头H与上下游水位差Z,以及关键参数A与B的计算确定方程式。
2.1 自由出流工况
当一般压力输水管道出口为自由出流运行工况,且为等管径,不考虑水流行进流速或行进流速微小可忽略不计,即行进流速v0=0时,则可依据(9)式得出压力水头H为:
(13)
由此可得:
A=0.082 7(∑ζi+1)Q2H-1
(13-1)
B=10.293 5Q2n2LH-1
(13-2)
2.2 淹没出流工况
当一般压力输水管道出口为淹没出流运行工况,并为等管径,不考虑水流行进流速或行进流速微小可忽略不计,即行进流速v0=0,且上下游进出口渠段水流流速相等或近似相同,即v1=v2=v3时,则可依据(9)式得出上下游水位差Z为:
(14)
由此可得:A=0.082 7∑ζiQ2Z-1
(14-1)
B=10.293 5Q2n2LZ-1
(14-2)
2.3 不同管径方程分析比较
对比(13)与(14)式,公式型式虽不同,但量值相等,对于水头损失系数总量,自由出流工况相对淹没出流工况,增加出口水头损失系数1.0;对比(12)与(14)式,公式型式虽相同,但量值不相等,(12)式中的水头损失系数总量并无出口淹没水头损失系数1.0,由此可知,一般压力输水管道为倒虹吸管的一种特例。
3 管径方程求解方法及其步骤
倒虹吸管与一般压力输水管道管径通用标准方程x4-Ax-B=0为一元四次方程,其求解方法相同。
令:
y=f(x)=x4-Ax-B=0
(15)
在求出方程(15)的实根后,即可求出倒虹吸管或一般压力输水管道的净管径d。方程f(x)=0的自由变量即为实根,也即为y=f(x)图形与x轴交点的横坐标,可采用牛顿法求解方程,其计算求解方法及其步骤一般分为以下5个环节程序:
(1)依据倒虹吸管与一般压力输水管道的运行工况、输水流量、上下游水头落差、工程布置、结构设计、水头损失系数、输水水力学计算特性参数与成果,以及运行或假定条件参数,求出相应关键参数A、B值,然后代入方程(15),得到相应管径方程式。
(2)求解满足f(A)·f(B)<0的封闭区间[A,B]值。
(3)求解f(x)的导数,得方程式:f′(x)=4x3-A、f″(x)=12x2>0。
(4)依据封闭区间[A,B],重复采用牛顿公式求解方程中的x值,分别可得以下两式:
(16)
(17)
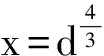
4 工程实例计算分析
4.1 工程例1
某引水工程渠道与河流交叉,采用预制钢筋混凝土倒虹吸管输水建筑物跨越,引水流量Q=3.2m3/s、进出口流速v1=v3=0.75m/s、上下游渠道水位总落差ΔH=0.58m;进出口设置渐变段,水头损失系数分别为ζ1=0.10、ζ2=0.28;进口渐变段末端断面流速v2=0.96m/s;管道长度L=182.40m;进口拦污栅水头损失系数ζ3=0.018、闸门门槽水头损失系数ζ4=0.05、进口水头损失系数ζ5=0.26、管道轴线两处转弯水头损失系数ζ6=ζ7=0.22;管道水力糙率n=0.013 5,要求计算确定倒虹吸管净管径d。
倒虹吸管管径d计算求解确定过程分为以下5个步骤:
(1)按照(11)及(11-1~2)式,可依据已知条件参数求得A=1.514、B=5.977。由此,倒虹吸管管径方程(10)式为x4-1.514x-5.977=0,(15)式相应为y=f(x)=x4-1.514x-5.977。
(2)对于(15)式,当取x=0时,f(0)=-5.977<0;经重复x不同参数值计算,可满足f(x)>0的最小下限x参数值为x=1.711,此时f(1.711)=0.002 9>0,由此,可得封闭区间[A,B]值为x∈[0,1.711]。
(3)相应可得f′(x)=4x3-1.514、f″(x)=12x2>0。
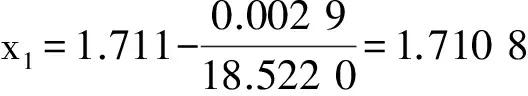
因此,根据管径方程式,可求解得f(1.710 8)=0.000 778≈0,故取x=1.710 8。
(5)计算d=1.710 83/4=1.495 9m。
最终计算确定倒虹吸管管道净管径为d=1.495 9m,工程设计净管径取d=1.50m。
4.2 工程例2
某供水工程供水水头H=5.2m,压力输水管道出口为自由出流,供水流量Q=1.2m3/s,输水管道为钢管,管道长度L=856.6m,管道进口水头损失系数ζ1=0.45,管道轴线五处转弯水头损失系数分别为ζ2=ζ3=0.22、ζ4=ζ5=ζ6=0.25,管道水力糙率n=0.012,要求计算确定压力输水管道净管径d。
压力输水管道管径d计算求解确定过程分为以下5个步骤:
(1)按照(13)及(13-1~2)式,可依据已知条件参数求得A=0.061、B=0.352。由此,压力输水管道管径方程(10)式为x4-0.061x-0.352=0,(15)式相应为y=f(x)=x4-0.061x-0.352。
(2)对于(15)式,当取x=0时,f(0)=-0.352<0;经重复x不同参数值计算,可满足f(x)>0的最小下限x参数值为x=0.796,此时f(0.796)=0.000 91>0,由此,可得封闭区间[A,B]值为x∈[0,0.796]。
(3)相应可得f′(x)=4x3-0.061、f″(x)=12x2>0。
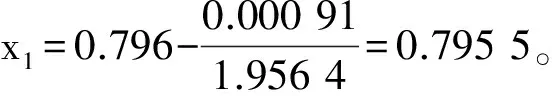
因此,根据管径方程式,可求解得f(0.795 5)=0.000 064≈0,故取x=0.795 5。
(5)计算d=0.795 53/4=0.842 3m。
最终计算确定压力输水管道净管径为d=0.842 3m,工程设计净管径取d=0.85m。
若管径d与水头H可灵活选择确定,则当选择确定净管径为d=0.842 3m时,可逆向由(13)式计算得出所需供水水头为H=5.2m。
5 结 语
在各类调水、引水及供水等水利工程中,为降低水量损失、减少工程占地、有效保护水质、确保供水压力水头,以及考虑输水线路布置灵活等需要,一般多采用压力管道输水。设计实践实际工作中,一般依据运行水头压力、压坡线、水头损失量、管材价格、经济流速,以及运输与安装施工等复杂多变因素,采用试算法计算确定管径d,由于可变因素较多,计算选择相对繁琐,且工作量较大。本文依据压力管流水力学计算理论,通过分析与方程推导,导出倒虹吸管径d及直接计算运行工作水头ΔH的通用标准方程x4-Ax-B=0求解法,并依据倒虹吸管进出口布置及其型式与结构的不同,分别归纳分析进出口设置与不设置渐变段的运行工作水头ΔH,以及关键参数A与B的计算确定方程式。进而得出倒虹吸管的特例,一般压力输水管道自由出流与淹没出流两种不同工况的管径d,以及直接计算压力水头H与上下游水位差Z,以及关键参数A与B的计算确定方程式,并进行分析比较。提出管径d方程求解方法及其步骤,计算选择简便快捷。同时,分别列举不同类型工程实例计算,进一步明确管径d方程求解方法及其步骤,计算结果准确,可为各类压力输水工程实践提供参考。
本文承蒙甘肃省水利水电勘测设计研究院副总工程师陈晓东审阅和指导,特此致谢!
2016-09-19
陈居乾(1992-),男,甘肃会宁县人,从事水力工程设计工作。
TU991.36
B
1003-9805(2016)04-0029-03

