基于量子绝热捷径技术的光波导分束器设计

浦珺慧,施解龙,吴仁华,陈玺

(上海大学理学院,上海　200444)

基于量子绝热捷径技术的光波导分束器设计

浦珺慧,施解龙,吴仁华,陈玺

(上海大学理学院,上海200444)

用于加快量子绝热“慢”过程的量子绝热捷径技术,已广泛应用于原子、分子和光物理.基于耦合波导的量子光学类比,利用量子绝热捷径技术设计光学波导的耦合系数与传播常数,实现快速的光波导分束器件.通过数值模拟,并与共振耦合和绝热耦合波导进行比较.结果表明,量子绝热捷径技术所设计的光学波导分束器具有长度短、输出稳定性高的优势.

集成光学；耦合波导；量子绝热捷径；光分束器

随着集成光学的发展,耦合波导在光通信中有着重要和广泛的应用,例如设计光定向耦合器、光开关、光调制器和光分束器等.特别地,光分束器作为重要的光通信器件,因其能将光能量、偏振等区分后分配到多个波导中从而实现一路到多路或多路到一路的光传输,而受到了极大的关注[1-2].理想的光分束器应具有低损耗、体积小、高带宽等优点.常见的能量分配型光分束器的设计结构有光纤拉锥型、Y分叉型和MMI型[3-5].

目前,共振耦合是实现波导耦合的一种简易的方式.采用该方式,波导间距不变,能量输出呈周期性变化,只有当波导长度满足特定值时,才能获取完美的能量输出.共振耦合波导对于波导参数和入射光波长等的变化较为敏感.于是,人们提出了绝热耦合波导耦合器.当满足绝热条件时,波导中的能量输出稳定,且对波导参数等控制要求不高,但是该耦合器的缺点是需要较长的波导距离来满足绝热条件.因此,人们通过对不同耦合模方程进行最优化设计,试图寻找到距离短、输出能量稳定的器件[6].但是最优化设计的数值计算过程往往需要迭代,不但费时而且不能得到解析表达式.

近年来,上海大学陈玺等[7-8]提出了量子绝热捷径技术,该技术通过加快绝热“慢”过程,实现了量子态的快速操控或制备.由于绝热过程普遍存在,量子绝热捷径技术被推广至导波光学和非线性光学并受到了广泛关注[9].基于量子光学与波导光学的类比[10-11],绝热捷径技术已被用于设计快速且稳定的波导定向耦合器[12-13]、模式转换器等[14-15].本工作主要利用量子绝热捷径技术,特别是Berry[16]提出的量子无摩擦动力学法,来设计波导的宽度和耦合系数,从而实现三波导中快速且稳定的1×2光分束器.

1　理论模型

首先考虑一个量子三能级体系[17],具体模型如图1所示.

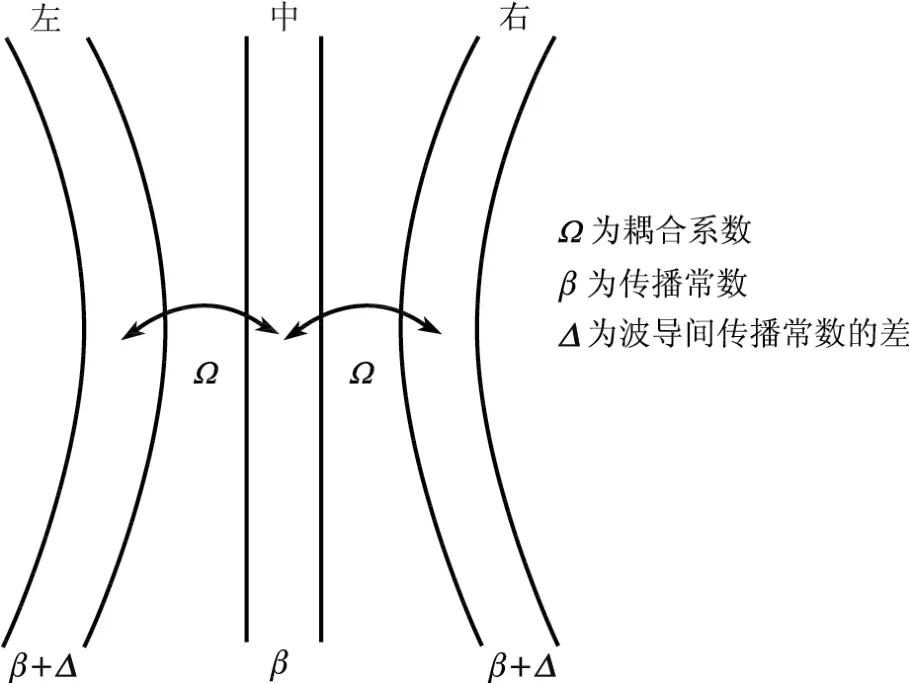
图1　三能级体系的光学波导类比Fig.1　Optical waveguides analogy of three-level systems

若令变量ħ=1,则该体系的哈密顿量可以写为

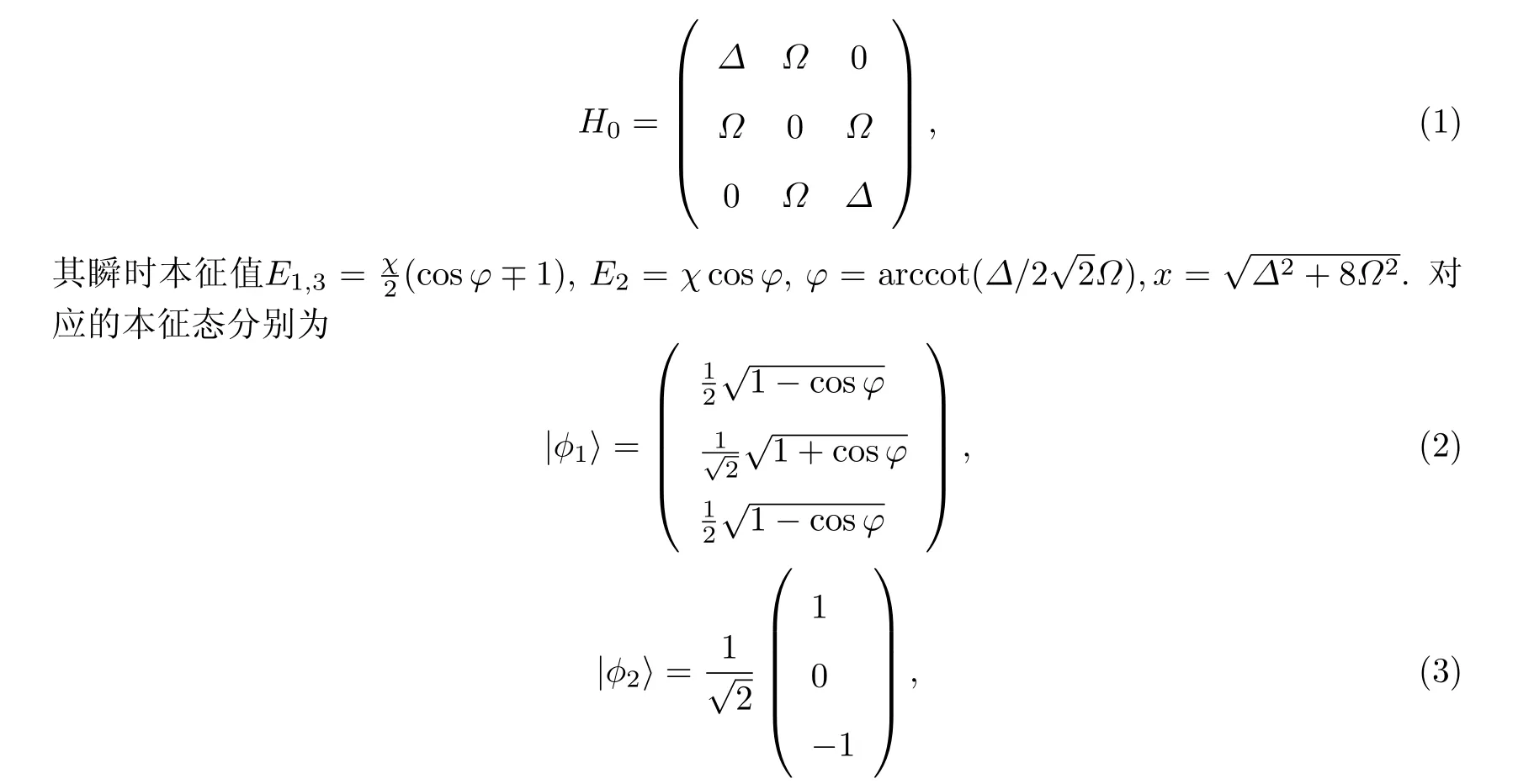
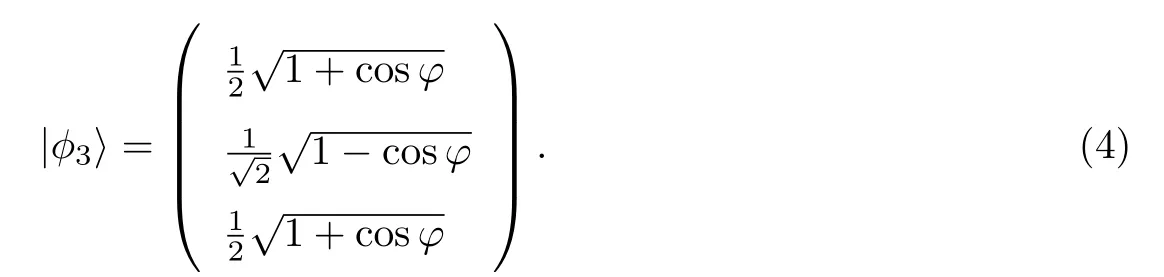
由式(1)～(4)可知,当满足绝热条件|˙ϕ|≪|χ|时,H0缓慢变化,则系统沿着瞬时本征态演化至末态输出,即绝热演变.然而,当绝热条件不满足时,系统则发生跃迁,转换效率降低.为了加快系统的绝热过程,本工作采用Berry[16]提出的量子无摩擦动力学法,构造哈密顿量H=H0+Hcd,其中Hcd的表达式为

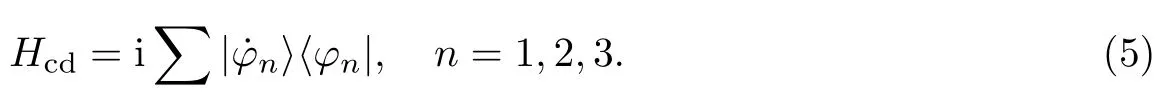
新的哈密顿量H的薛定谔方程的解恰恰是原哈密顿量H0的绝热近似解,但是Hcd在物理上难以实现[18].为此,引入变换矩阵

并对哈密顿量H作幺正变换,

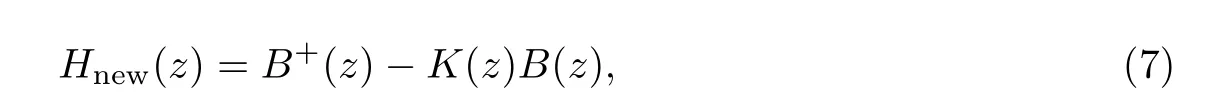
同时,设定

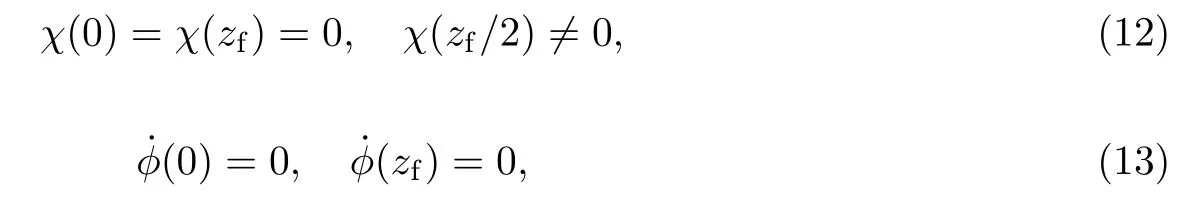
以满足Hnew(0)=0,Hnew(zf)=0,使得波导的输出和输入端处波导之间的耦合效应近乎为0.另外,进一步设定

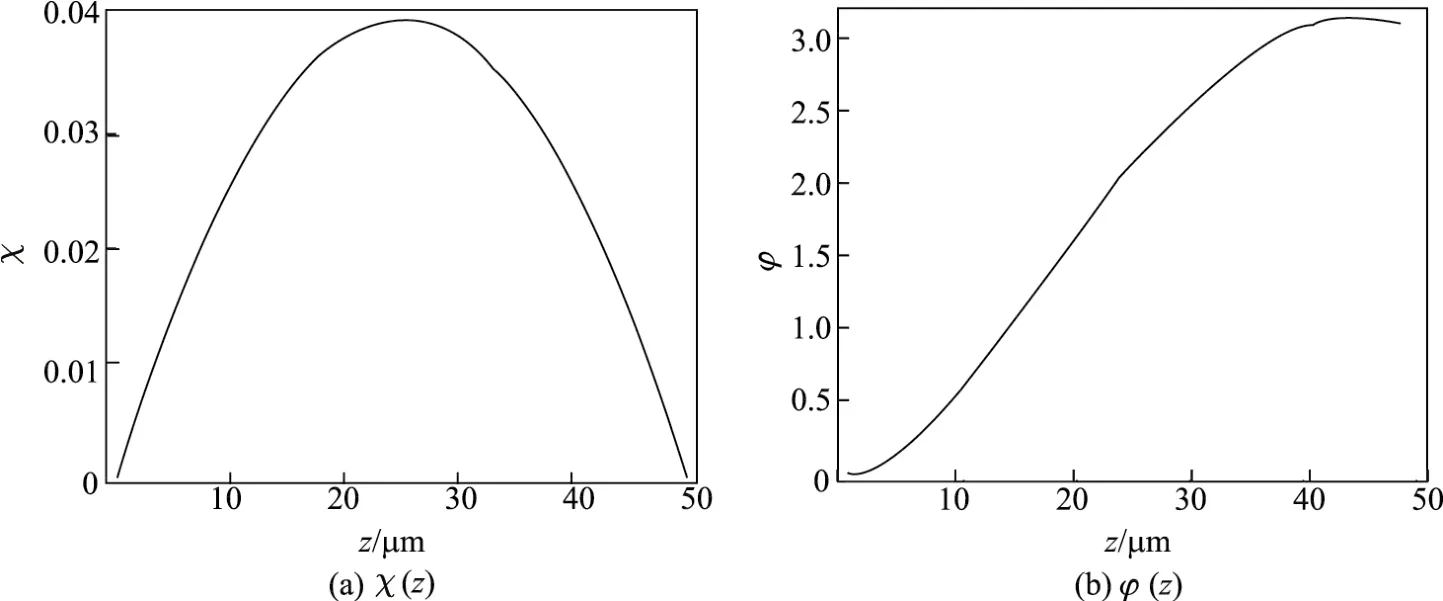
图2　参数χ(z),ϕ(z)随距离z的变化Fig.2　Parameters χ(z),ϕ(z)versus z

将χ(z)与ϕ(z)代入式(8)～(9),得到光波导的耦合系数~Ω和传播常数差~∆,如图3所示.由于选取的波导长λ=1.55µm较小,绝热条件不满足,因此运用该绝热耦合型波导无法实现完美的1×2光分束.

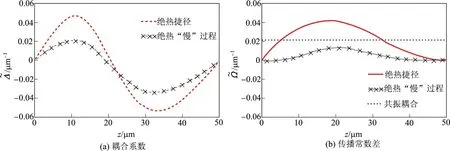
图3　3种光分束器系统的耦合系数和传播常数差Fig.3　Coupling efficiency and mismatch of propagation constant for three different waveguide systems

2　数值模拟与比较

为了验证上述理论结果,利用光束传播法[19]进行数值模拟.假设二维波导由折射率nc=2.3的材料构成,包层为空气(折射率ncl=1).入射光中心波长λ=1.55µm,TE偏振.要设计上述二维波导,就需要对3根波导的宽度以及相互间的距离进行设计.在近似对称波导中耦合系数Ω与波导间距满足如下指数关系[20]：

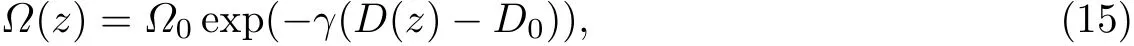
式中,Ω0=0.661 907,γ=7.596 92,D0=0.5µm.以中间波导的中心为基准线,将式(9)代入式(14),计算得到D(z),即左、右波导的中心到中间波导中心的距离.另外,利用传播常数与波导宽度之间的近似关系[21-22]：

通过调整中间波导的宽度变化,可以计算得到中间波导与两边波导的传播常数差~∆.这里选取WM为波导实际宽度,左右波导的基准宽度为W=0.5µm.根据式(7)所设计的耦合光分束器的光能量分布和功率演化如图4所示.

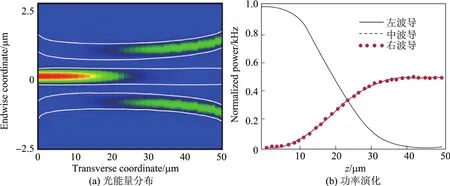
图4　1×2绝热捷径耦合光分束器的光传输模拟Fig.4　Beam propagation simulations for 1×2 shortcut coupler beam splitter

为了进一步与原有的波导分束器作比较,这里给出共振耦合分束器的光能量分布和功率演化,如图5所示.研究结果表明：在波导参数相同的情况下,绝热捷径耦合分束器的输出能量更为稳定,对波导折射率和入射光波长等参数的变化不敏感.

图6为绝热捷径耦合分束器和共振耦合分束器波导输出功率损耗随波长的变化，可以看出利用量子绝热捷径所设计的分束器对波长的敏感性小于共振分束器,其光谱频带较宽,有利于设计宽波带的光分束器.

图5　共振耦合分束器的光传输模拟Fig.5　Beam propagation simulations for resonant coupler beam splitter

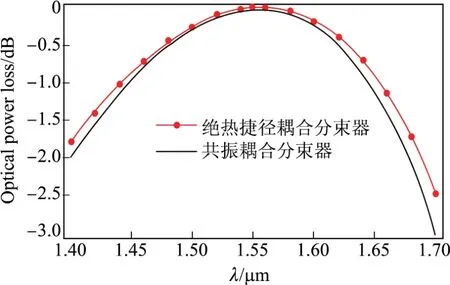
图6　波导输出功率损耗随波长的变化Fig.6　Output power loss versus input wavelength

3　结束语

本工作研究了量子绝热捷径技术在耦合波导中的应用,设计了1×2耦合光分束器.通过与共振分束器的比较,发现基于量子绝热捷径技术所设计的光分束器具有长度短、输出稳定、对入射波长变化不敏感等优势.这不仅拓展了量子绝热捷径技术的运用,而且对集成光波导的设计具有重要的指导意义.在接下来的工作中,还将针对入射波长变化等微扰因素对波导进行最优化设计,并进一步推广至1×3甚至1×N的光分束器.

[1]FUjII Y,MINOwA J.Four-channel wavelength multiplexing composed of phase plates and polarizing beam splitters[J].Applied Optics,1989,28(7)：1305-1308.

[2]底彩慧,周常河.基于达曼光栅的动态光耦合器[J].光学学报,2007,27(7)：1275-1278.

[3]黄勇,曾庆济.一种新型结构的单模光纤1×4分束器[J].光学学报,1995,15(2)：248-251.

[4]唐雄贵,廖进昆,李和平,等.新型非对称Y分支波导设计与分析[J].光学学报,2009,29(8)：2077-2081.

[5]HOSSEINI A,KwONG D N,ZHANG Y,et al.1×N multimode interference beam splitter design techniques for on-chip optical interconnections[J].IEEE Journal of Selected Topics in Quantum Electronics,2011,17(3)：510-515.

[6]RAMADAN T A,ScARMOzzINO R,OSGOOD R M.Adiabatic couplers：design rules and optimization[J].Journal of Lightwave Technology,1998,16(2)：277-283.

[7]CHEN X,RUScHHAUpT A,ScHMIDT S,et al.Fast optimal frictionless atom cooling in harmonic traps：shortcut to adiabaticity[J].Phys Rev Lett,2010,104(6)：063002.

[8]CHEN X,LIAUAIN I,RUScHHAUpT A,et al.Shortcut to adiabatic passage in two-and three-level atoms[J].Phys Rev Lett,2010,105(12)：123003.

[9]TORRONTEGUI E,IBANEz S,MARTINEz-GARAOT S,et al.Shortcuts to adiabaticity[J].Advances in Atomic Molecular&Optical Physics,2013,62(1)：117-169.

[10]VITANOv N V,GARRAwAy B M.Landau-Zener model：effects of finite coupling duration[J]. Physical Review A,1996,53(6)：4288-4340.

[11]BERGMANN K,THEUER H,SHORE B W.Coherent population transfer among quantum states of atoms and molecules[J].Reviews of Modern Physics,1998,70(3)：1003-1025.

[12]TSENG S Y.Counterdiabatic mode-evolution based coupled-waveguide devices[J].Optics Express,2013,21(18)：21224-21235.

[13]TSENG S Y,WEN R D,CHIU Y F,et al.Short and robust directional couplers designed by shortcuts to adiabaticity[J].Optics Express,2014,22(15)：18849-18859.

[14]LIN T Y,HSIAO F C,JHANG Y W,et al.Mode conversion using optical analogy of shortcut to adiabatic passage in engineered multimode waveguides[J].Optics Express,2012,20(21)：24085-24092.

[15]TSENG S Y,CHEN X.Engineering of fast mode conversion in multimode waveguides[J].Optics Letters,2012,37(24)：5118-5120.

[16]BERRy M V.Transitionless quantum driving[J].Journal of Physics A：Mathematical and Theoretical,2009,42(36)：2285-2289.

[17]MARTINEz-GARAOT S,TORRONTEGUI E,CHEN X,et al.Shortcuts to adiabaticity in three-level systems using Lie transforms[J].Physical Review A,2014,89(5)：053408.

[18]IBANEz S,CHEN X,TORRONTEGUI E,et al.Multiple Schr¨odinger pictures and dynamics in shortcuts to adiabaticity[J].Physical Review Letters,2012,109(10)：100403.

[19]KAwANO K,KITOH T.Introduction to optical waveguide analysis：solving Maxwell’s equations and the Schr¨odinger equation[M].New York：John Wiley&Sons Inc,2001：165-180.

[20]OKAMOTO K.Fundamentals of optical waveguides[M].Hoboken：John Wiley&Sons Inc,2007：177-178.

[21]SyAHRIAR A,ScHNEIDER V M,AL-BADER S.The design of mode evolution couplers[J].Journal of Lightwave Technology,1998,16(10)：1907-1914.

[22]SOLDANO L B,PENNINGS E C M.Optical multi-mode interference devices based on self-imaging：principles and applications[J].Journal of Lightwave Technology,1995,13(4)：615-627.

Beam splitter in optical waveguides designed by shortcuts to adiabaticity

PU Junhui,SHI Jielong,WU Renhua,CHEN Xi
(College of Sciences,Shanghai University,Shanghai 200444,China)

Shortcuts to adiabaticity have been proposed to accelerate“slow”adiabatic processes with the applications in atom,molecular and optical physics.Based on the quantum optical analogy of coupled waveguide,the coupling coefficient and propagating constant are designed by using shortcuts to adiabaticity,to realize optical beam splitters in short length.Compared with resonant and adiabatic couplers by numerical simulation,the designed waveguide is demonstrated its advantages on shorter length and high stability.

integrated optics；waveguide coupler；shortcuts to adiabaticity；beam splitter

O 436

A

1007-2861(2016)05-0545-07

10.3969/j.issn.1007-2861.2015.02.007

2015-03-24

国家自然科学基金资助项目(11474193,61176118)；上海市浦江人才计划资助项目(13PJ1403000)；教育部博士点基金资助项目(2013310811003)；上海市高校特聘教授“东方学者”资助项目

施解龙(1960—),男,副教授,博士,研究方向为光波导理论.E-mail:sjlong@staff.shu.edu.cn