离心纺:一种高效制备微/纳米纤维的纺丝方法(二)
徐淮中 陈欢欢 李祥龙 刘 晨 杨 斌
浙江理工大学材料与纺织学院,浙江 杭州 310018
离心纺:一种高效制备微/纳米纤维的纺丝方法(二)
徐淮中 陈欢欢 李祥龙 刘 晨 杨 斌
浙江理工大学材料与纺织学院,浙江 杭州 310018
(上接2016年第1期第33页)
3 射流成形机理
有喷嘴离心纺、无喷嘴离心纺、离心-静电纺有着各自的特点,下文将重点介绍这三种离心纺射流的成形条件、轨迹特征和影响因素。其中,有喷嘴和无喷嘴离心纺的射流成形机理将基于本课题组的研究成果展开论述,而离心-静电纺的射流成形机理将基于台湾成功大学Chen Chuh-yung课题组近4年来的科研成果展开分析,以期为不同的纺丝原料选择合适的纺丝类型和纺丝参数提供部分理论和试验依据。
3.1 有喷嘴离心纺
在离心力的作用下,纺丝液沿纺丝甬道向外运动。流体在圆管中的运动称为泊肃叶(Poiseuille)流动,而基于该模型推导得到的哈根-泊肃叶(Hagen-Poiseuille)方程已广泛应用于化工领域。
3.1.1 临界转速
纺丝液从针头内挤出的瞬间及其示意如图15[51]1551所示。

图15 高聚物流体从针头内挤出瞬间
此时,半球形液滴主要受黏滞力(Fv)、表面张力(Fγ)及离心力(Fc)的共同作用。其中:
Fv=πdγsinθ
(2)
(3)
Fc=ρVpdrΩ2
(4)
式中:d——喷嘴内径;γ——表面张力;θ——液滴与喷嘴夹角;L2——针头后部长度; ΔP——作用于针头两端(即L2段)的压差; ρ——纺丝液密度;Vpd——液滴体积;r——喷丝器半径;Ω——临界转速。
当Fv、Fγ及Fc三者满足平衡方程Fv+Fγ=Fc时,可得到有喷嘴离心纺丝临界转速(Ωnozzle-c):
(5)
当作用于液滴的Fc足以克服Fv与Fγ时,液滴向外拉伸、变形,形成射流。
3.1.2 射流初速度
射流离开喷丝器时的速度即为射流初速度(uex),其会直接影响射流轨迹及最终纤维的形貌。针对图15(b)所示的物理模型可得:
(6)
式中:L1——针头前部长度;r1、r2——原点(O)分别至针头前部质心(CM1)和后部质心(CM2)的长度;μ——流体黏度系数。
式(6)左端为离心力项,右端为动量和摩擦损耗项,化简后可得:
(7)
3.1.3 初始射流的牵伸
射流在达到稳定状态前会经历一段不稳定的牵伸运动,如图16[51]1554所示:半球形液滴在克服表面张力与黏滞力后,经牵伸形成缩颈;射流离开喷嘴后,惯性力因空气阻力作用而逐渐减小,黏滞阻力随溶剂挥发而逐渐增大,导致拉伸射流的合外力及其产生的绝对速度逐渐减弱,射流角速度在做离心运动的过程中逐渐减小并滞后于喷嘴;端部液滴由于质量大导致其绝对速度大于射流缩颈处速度,非线性的角速度差异形成了初始射流独特的反S形轨迹;射流被牵伸数圈后形成稳定的螺旋轨迹(图17[51]1555)。
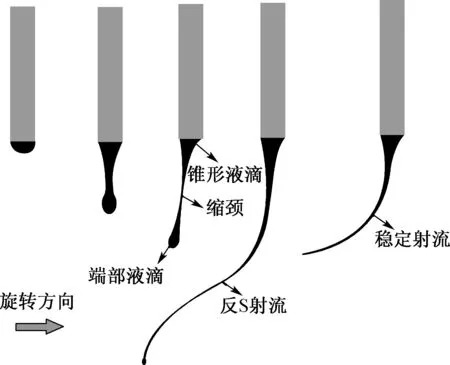
图16 离心纺初始射流拉伸过程示意
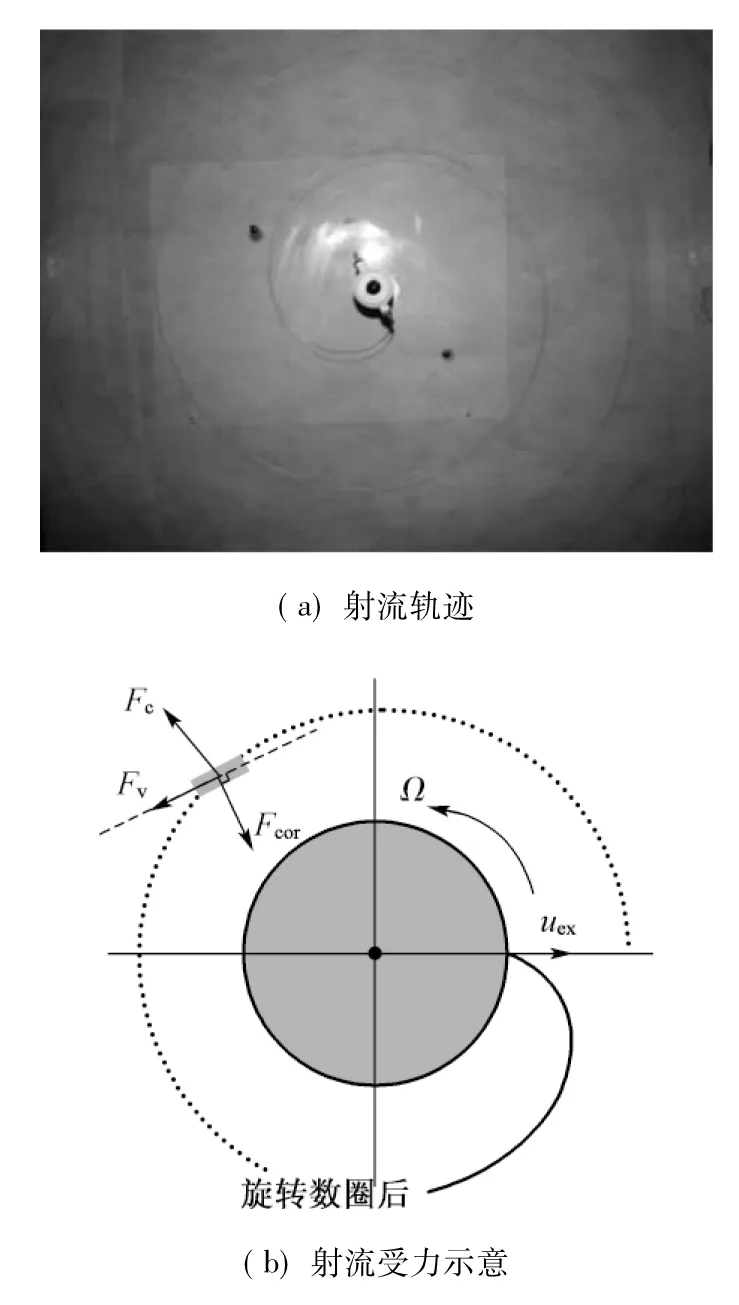
图17 PVP溶液离心纺射流轨迹(PVP水溶液 质量分数18%,转速4000r/min)
3.1.4 螺旋射流轨迹
射流稳定后,轨迹呈曲率半径逐渐增大但增幅逐渐减小的螺旋形,此时,射流受离心力(Fc)、黏滞力(Fv)和科氏力(Fcor)的共同作用,如图17(b)所示。Fc沿径向向外拉伸射流,使射流逐渐变细;Fv使射流保持连续而不断裂;Fcor垂直射流轴线向内,促使射流弯曲形成螺旋轨迹。该轨迹可使直径约1mm 的初始射流在狭小空间内直径迅速拉伸至微米或亚微米级,即射流牵伸了近4000倍。且随着射流向外扩张,Fc逐渐减小、Fv逐渐增加,作用于射流的合外力减小,导致射流不断趋紧,从而验证了Taghavi-Larson模型的合理性。
Padron等[52]分析了不同参数条件下离心纺的射流轨迹,发现:PEO射流先向外扩张,达到最大半径后向内收缩[图18(a)];转速越高或纺丝液质量分数越低,射流曲率半径越大[图18(b)、18(c)];针头沿旋转方向弯曲角度越大、喷嘴长径比越小,射流曲率半径越大[图18(d)、18(e)];储料槽内纺丝液含量越多,则作用于喷嘴的压力越大,射流曲率半径也越大[图18(f)]。射流曲率半径会直接影响射流固化时间、固化点与牵伸倍数,最终影响纤维形貌及其力学性能。本课题组研究还发现,PEO与PVP的射流轨迹区别较大,它们分别代表了两种类型的射流轨迹:PVP大分子链含侧基,纺丝液黏弹性较低,射流会持续向外扩张;PEO为直链大分子,纺丝液黏弹性高,靠近喷嘴时离心力起主导作用,远离喷嘴时黏滞力起主导作用,因此PEO轨迹有临界半径,且该临界半径随转速提高、纺丝液质量分数降低而变大。因此,建议PVP纤维采用环形收集器或输网帘收集,而PEO纤维因需借助气流或静电等辅助外力改变射流轨迹,建议采用输网帘+气流或输网帘+静电的方式收集。

图18 PEO离心纺射流轨迹
3.2 无喷嘴离心纺
无喷嘴离心纺射流离开喷丝器后的运动轨迹及规律与有喷嘴离心纺射流一致,本节将重点介绍无喷嘴离心纺的“手指”现象、临界转速及射流初速度。
3.2.1 “手指”现象
流体经导流器狭缝中挤出后,液膜前端会产生不稳定波动[图19(a)],并在波峰处形成“手指”[图19(b)],且随着流体进一步向外铺展,液膜前端不断分裂出新“手指”[图19(c)][51]1549。

图19 质量分数为20%的PVP水溶液在 旋转盘面上的铺展过程
液膜分裂形成“手指”可利用Rayleigh-Taylor不稳定性理论解释。研究发现,液膜厚度随着铺展距离增大而变薄,这使得作用于液膜前端的表面张力不断变大,进而产生波动。当离心力足以克服表面张力时,波动发展并形成“手指”,否则波动将被抑制。因此,液膜厚度与离心力是产生“手指”的两个关键因素。
3.2.2 临界转速
纺丝液离开导流器时,会在导流器狭缝出口处形成“凸起”[图20(a)和(b)][51]1552-1553。
因表面张力(Fγ)与黏滞力(Fv)会抑制流体向外运动,故可建立离心力Fc=ρVr0Ω2、表面张力Fγ=γhl/r*及黏滞力Fv=μΔPh2l/(2r0)之间的平衡方程:
(8)
式中:μ——黏度系数; ΔP——作用于r0段的压差;h、l——狭缝高度与长度;r0——导流器半径;r*、V——凸起的曲率半径与体积;ρ——流体密度;Ω——喷丝器转速。
因此,流体从导流器中挤出时喷丝器的临界转速(Ωlid-c):
(9)
流体从导流器中挤出后液膜均匀铺展于旋转盘面[图20(c)],并在流体最前端(三相接触线处)形成隆起,此处产生向内的压差ΔP=γ/r*[图20(e)],抑制液膜向外运动。在液膜隆起处建立平衡方程(等式左端分别为黏滞力项和表面张力项,右端为离心力项):
(10)
式中:rMin——最小半径;δ——液膜厚度;S——隆起侧面积。
因此,液膜向前运动的喷丝器临界转速(Ωfilm-c):
(11)
同样,在“手指”隆起处建立平衡方程[图20(d)和(e)]:
(12)

图20 固、液、气三相接触线处的凸起
式中:rMax——最大半径;wf——“手指”宽;Vdp——隆起体积。
因此,形成“手指”的临界转速(Ωfinger-c):
(13)
式(5)、式(9)的临界转速在约束条件下求得,而式(11)、式(13)的临界转速在自由面环境下求得。流体在无喷嘴离心纺喷丝器内经历的过程更为复杂,三类临界转速遵循:Ωlid-c<Ωfilm-c<Ωfinger-c。
3.2.3 射流初速度
在极坐标系(r,θ,z)中,流体沿盘径向的动量方程:
(14)
式中,ρrΩ2为离心力项,∂τrz/∂z为黏滞力项,τrz=K(∂vr/∂v)n为剪切应力。
利用边界条件:vr=0、 z=0、 ∂vr/∂z=0、 z=δ,积分并化简式(14),可得到盘径向速度(vr):
(15)

试验发现,流体在盘面上的流动速度较低(每秒仅数十毫米),即高聚物流体剪切变稀效果不显著。取n=1,此处用牛顿流体黏度系数η代替非牛顿流体稠度系数K,化简式(15)可得:
(16)
进一步求得射流的初速度(uex):
(17)
式中:R——纺丝盘半径。
由于缺少喷嘴,流体在纺丝盘上受到的抑制作用较小,故相同纺丝条件下无喷嘴喷丝器形成的射流初速度更大。因此,建议选用无喷嘴离心纺加工高黏度纺丝液。
3.3 离心-静电纺
静电纺射流轨迹如图21(a)所示,喷嘴出口处液滴受静电拉伸作用形成泰勒锥,射流随即从锥点处喷出,并在运行一小段距离后发生不稳定鞭动,形成螺旋弯曲,且螺旋半径不断增大,并伴随出现2、3级螺旋;当静电场中引入离心力后,鞭动现象消失,射流沿垂直于喷丝器轴线方向弯曲、扩张[图21(b)][53]。静电纺射流螺旋弯曲源于射流表面相邻正电荷的相斥作用,当引入离心力后,为达到新的平衡,因电荷斥力引起的鞭动现象消失,科氏力驱使射流形成螺旋轨迹。

图21 静电纺与离心-静电纺射流轨迹比较
离心-静电纺射流轨迹融合了离心纺与静电纺射流的轨迹特点,其射流在离开喷嘴不久后便形成了120°转折[图22(a)],替代了传统静电纺射流的鞭动现象[54];且弯曲不稳定现象消失使得射流受到更加剧烈的剪切作用,直接促使射流变得更细、更长,提高了纤维的力学性能。若将电压从25kV提升至30kV,则双酚A聚碳酸酯(BPAPC)纤维的平均直径将从270nm变成340nm,原因在于电压提高后,射流弯曲不稳定作用增强,这不利于射流的充分牵伸。若将纺丝液温度从25℃提高至45℃,射流则将出现劈裂现象[图22(b)],因为提高纺丝液温度会加速溶剂挥发,射流表面张力增大,从而促进了电荷的积聚,导致射流劈裂。综上,离心-静电纺射流既具有离心纺射流的螺旋轨迹特征,又具有静电纺射流独有的劈裂特性,因此应通过主动调控纺丝参数(如纺丝液性能、操作条件、环境条件等),抑制不利于纺丝的射流运动行为(如射流鞭动),实现充分拉伸射流与提高纤维力学性能的目标。
离心-静电纺射流轨迹与纺丝液黏度、表面张力、转速、电场强度、介电性质等参数有关。为方便研究,引入特征数Re(惯性力与黏滞力之比)和We(惯性力与表面张力之比)表征射流曲率半径,特征数Pe(电对流与电导之比)和ε(静电力与惯性力之比)表征射流长度,特征群П1(静电力与黏滞力之比)和Oh(黏滞力与表面张力之比)表征泰勒锥形貌(图23[55]546)。

(a) 电压25kV,转速800r/min,溶液温度25℃

(b) 电压25kV,转速800r/min,溶液温度45℃(射流出现劈裂现象)

图23 离心-静电纺射流曲率半径、射流长度、泰勒锥形貌与特征数(群)的关系
从图23可以看出,在合理的参数范围内,增大特征数Re、We、Pe、ε,射流受到的惯性力作用和电场力牵伸作用增强,这会导致射流轨迹的曲率半径变大、射流变细;减小特征群П1和Oh会诱发射流产生波动,断裂后形成珠粒,故П1和Oh越大,泰勒锥形貌越稳定,越易形成连续的射流。
Chen Chuh-yung课题组在此基础上分析了特征数(Re、We)、特征群(П1、Oh)与纤维可纺性(如纤维形貌、直径、力学性能)之间的关系。Re数与纤维直径、形貌关系如图24(a)所示,所纺材料依次为聚碳酸酯(PC)、聚乳酸(PLA)、聚丙烯腈(PAN)纤维[55]547-550,研究结果表明:静电场越大,Re数越大,射流螺旋轨迹的曲率半径也越大,因此越会有充分的力与时间拉伸射流,最终得到更细的纤维;反之,若静电力不足,Re数减小,射流未被充分拉伸,纤网中则会含有珠粒或串珠结构;相同纺丝条件下,降低纺丝液质量分数会使得Re数变大,但大分子链缠结度也随之降低,导致纤维中的珠粒含量增加。We数与纤维形貌的关系如图24(b):We>10.0,纤维均匀性及力学性能优异;We<1.2,仅有液滴形成。单纤维力学性能与特征群П1、Oh数的关系如图24(c):П1数越大,射流拉伸越充分;Oh数越大,则越不易形成串珠结构。因此,随着П1和Oh数变大,纤维的结晶度、硬挺度、取向度及模量均有提高。通过特征数(群)来加强运动射流与纤维形成关系的构想,为研究纤维可纺性提供了新思路。研究离心纺纤维成形时,若能针对性地从黏弹性射流本构模型中提炼出特征数(群),避免主观选用特征数(群)带来的误差,将能更准确地预测和调控离心纺射流运动及其纤维的可纺性,从而更精确地构筑运动射流与纤维可纺性之间的非线性响应关系,为预测和调控纤维的直径、形貌及其力学性能提供一定的理论和试验依据。
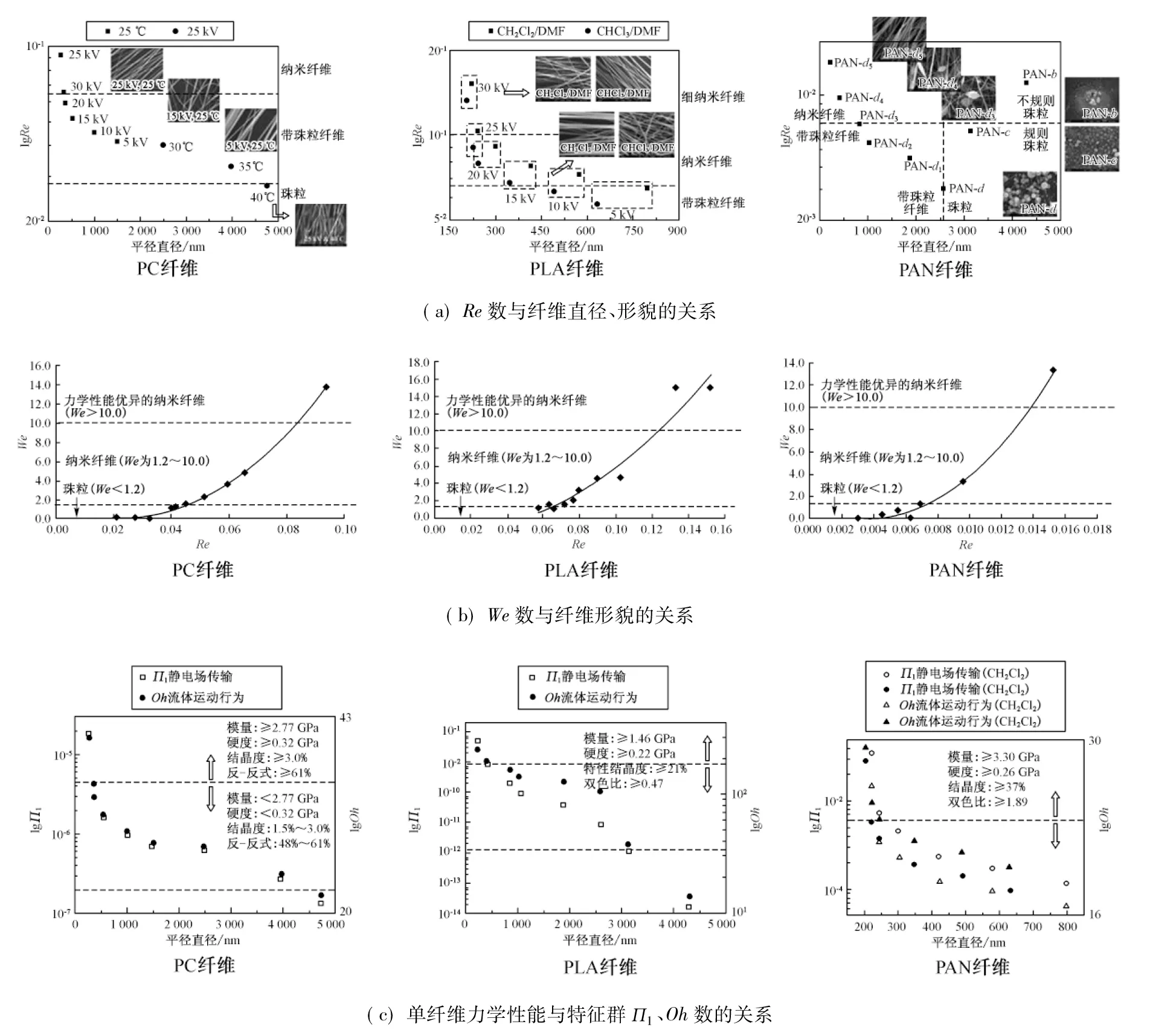
图24 离心-静电纺纤维形貌、直径、力学性能与特征数(群)间的关系
4 结论
离心纺作为一种制备纳米纤维的新方法,为制备高聚物纤维、无机物纤维和金属纤维提供了新选择。而基于离心纺技术发展的无喷嘴离心纺和离心-静电纺技术使得纤维的可纺性得到了进一步提升。无喷嘴离心纺利用自由面替代喷嘴,克服了喷嘴易堵塞的弊端,进一步提高了纤维产量;在离心场中引入高压电场,有助于消除鞭动现象,从而充分牵伸射流,提高纤维力学性能,形成致密纤网。研究纺丝参数对射流轨迹及纤维品质的影响规律时,应先归纳具有同类物理意义的纺丝参数,以特征数和特征群作为研究的基本单元,利用特征数(群)搭建射流形成与纤维可纺性之间的关系。此研究方法同样适用于静电纺、熔喷纺与常规化纤纺丝,是解决多参数问题的有效手段。
(全文完)
[51] XU H, CHEN H, LI X, et al. A comparative study of jet formation in nozzle- and nozzle-less centrifugal spinning systems[J]. Journal of Polymer Science Part B: Polymer Physics, 2014, 52(23).
[52] PADRON S, FUENTES A, CARUNTU D, et al. Experimental study of nanofiber production through forcespinning[J]. Journal of Applied Physics, 2013, 113(2):024318.[53] LIAO C C, HOU S S, WANG C C, et al. Electrospinning fabrication of partially crystalline bisphenol a polycar-bonate nanofibers: The effects of molecular motion and conformation in solutions[J]. Polymer, 2010, 51(13):2889.
[54] LIAO C C, WANG C C, SHIH K C, et al. Electrospinning fabrication of partially crystalline bisphenol a polycarbonate nanofibers: Effects on conformation, crystallinity, and mechanical properties[J]. European Polymer Journal, 2011, 47(5): 919.
[55] CHANG W M, WANG C C, CHEN C Y. The combination of electrospinning and forcespinning: Effects on a viscoelastic jet and a single nanofiber[J]. Chemical Engineering Journal, 2014, 244(5).
Centrifugal spinning: A high-efficient approach to fabricate micro-/nano-fibers(Part 2)
XuHuaizhong,ChenHuanhuan,LiXianglong,LiuChen,YangBin
College of Materials and Textiles,Zhejiang Sci-Tech University, Hangzhou 310018, China
2015-03-16
徐淮中,男,1989年生,在读硕士研究生,研究方向为离心纺纤维的成形机理
杨斌,E-mail: yangbin5959@zstu.edu.cn
TQ340.64
A
1004-7093(2016)03-0021-08

