基于MRAS的永磁同步电动机无位置传感器控制

邓 鹏

(荆楚理工学院，荆门 448000)



基于MRAS的永磁同步电动机无位置传感器控制

邓 鹏

(荆楚理工学院，荆门 448000)

为了实现永磁同步电动机(PMSM)无位置传感器控制，提出了一种基于永磁同步电动机两相静止α-β坐标系下PMSM数学模型的模型参考自适应(MRAS)位置估算算法。该算法利用α-β坐标系下的α轴和β轴电压、电流及其偏差，借助Lyapunov稳定性理论建立了PMSM位置估算模型，并根据该理论推导出位置参数的自适应率，保证了位置估算模型的稳定性和误差的收敛，同时快速有效地估算出了转子位置。仿真和实验结果证明了该位置估算算法的可靠性和有效性。

永磁同步电动机；模型参考自适应；位置估算

0 引 言

由于永磁同步电动机(以下简称PMSM)具有高功率密度、高效率、结构简单等特点，在驱动控制领域受到了普遍的关注。在PMSM的驱动控制系统中需要精确的转子位置来实现磁场定向，需要转子速度信息实现闭环控制，这就需要在电机轴上安装光电编码器、旋转变压器等位置传感器，但是，安装位置传感器不仅增加了系统的成本，系统体积也有所增加，并且传感器的安装和维护困难，限制了PMSM在相对恶劣环境条件下的应用。因此，永磁同步电动机无位置传感器控制的重要性日益凸显。目前，以观测器为基础的估算方法，利用电机凸极效应的高频注入法，扩展卡尔曼滤波法都属于观测器方法的范畴[1-2]，并得到了广泛的研究，但这些方法算法较为复杂，算法中的一些参数的设置影响其估算性能；高频注入法虽不依赖于电机的模型，但高频信号地注入会带来高频的噪声干扰，从而影响系统的性能[3]。综合上述情况，模型参考自适应算法由于是根据稳定性理论来设计参考系统，保证了系统的稳定型和鲁棒性，因此得到了广泛的应用。

模型参考自适应算法(以下简称MRAS)的要点主要为收敛算法的设计，首先，收敛算法需要保证待估模型与参考模型之间的输出误差能够收敛到零[4-8]；其次，为了实现转速位置实时计算，必须使得待估模型中估算的转子位置能够逼近实际位置。目前学术界比较常用的收敛算法主要有：局部参数最优化方法，基于Popov稳定理论的收敛算法设计，基于Lyapunov稳定性理论的收敛算法设计。

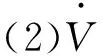
当确定的Lyapunov函数正定时，依据第(2)条件即可推导出转子位置的收敛率。本文将在PMSM的α-β坐标系下利用Lyapunov稳定性理论来设计待估模型中转子位置的自适应率。利用Lyapunov稳定性理论设计转子位置估算系统的主要过程如下：(1)对设定的MRAS位置估算系统，推导出转子位置误差方程；(2)确定一个正定函数V(x)作为Lyapunov函数；(3)对于V(x)，求出Lyapunov函数沿转子位置误差方向上的导数；(4)假设该导数为负定函数，建立等式，计算出转子位置收敛率。

本文在PMSM的α-β坐标系下，根据MRAS计算出的转子位置收敛率对PMSM转子位置进行估算，以李亚甫洛夫稳定性理论为基础，根据待估模型与参考模型二者之间的误差建立了转子位置计算模型，并推导出了转子位置的自适应率，保证了在一定条件下位置参考系统的稳定性和参数的收敛性。最后通过仿真验证了该方法的有效性和可靠性。

1 矢量控制下的PMSM位置估算

1.1PMSM数学模型的建立

在PMSM数学模型的推导中通常需要作以下设定[9-10]：(1)不考虑铁心磁路饱和； (2)忽略磁滞损耗和涡流损耗；(3)不考虑转子上的阻尼绕组和永磁体的阻尼作用；(4)反电动势为正弦。

1.2PMSM位置估算系统

PMSM在两相α-β静止坐标系下的数学模型：

(1)

式中：iα，iβ为定子α，β轴电流；uα，uβ为定子α，β轴电压；eα，eβ为永磁体反电动势α，β轴分量；Rs，Ls为定子电阻、dq轴等效电感；ψf为永磁体磁链；ωr为转子相角速度；θ为转子位置。

由反电势的表达式可以看出：反电动势中含有PMSM转子位置参数和转速参数。因此，利用MRAS算法估算出PMSM反电动势就能进一步计算转子位置和转速。

根据PMSM矢量控制原理，可得矢量控制下PMSM的MRAS位置估算系统结构图，如图1所示。

图1 矢量控制下PMSM的MRAS位置估算系统结构图

根据id=0控制，驱动系统为双闭环架构，控制器采用典型的PI控制。图2给出了转速位置系统结构图，该位置估算系统仅需要α，β轴电压和电流作为输入信号，这些参数可通过电流电压传感器测得后经过坐标变换获得，有利于算法在实际系统下应用。

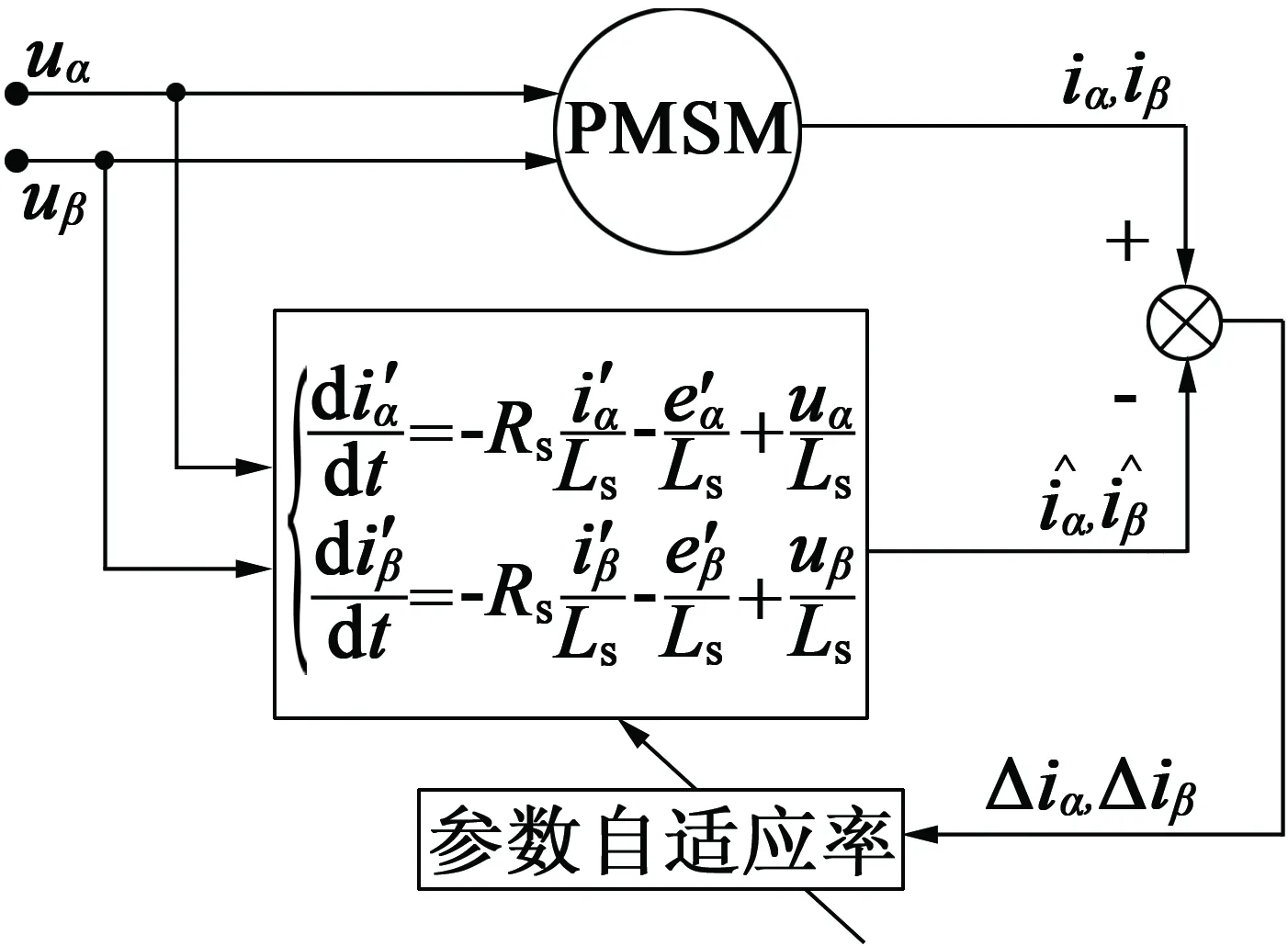
图2 MRAS转速位置系统结构图

2 PMSM模型参考自适应位置估算

2.1 位置估算模型的构建

MRAS算法是基于稳定性理论为前提条件来推导出待估参数收敛的算法，能够确保整个位置估算系统的稳定性，常用的自适应控制方法有[11-13]：MIT规则、Lyapunov稳定性判据和Popov稳定性判据。Lyapunov稳定性判据和Popov稳定性判据都是基于稳定性理论进行设计，对算法的收敛性有所保证，故应用广泛。

在估算转子位置过程当中，将PMSM的电压电流输出作为参考模型，将含有电机位置参数的PMSM数学模型看作待估模型，两模型之间的输入和输出可通过电压电流传感器测得。由两模型的输出误差和计算出的收敛算法来对电机位置进行估算，最终使得估算位置逼近到实际值。

本文利用实际的PMSM作为参考模型，将含有待估位置量的α-β坐标系下的PMSM的电压电流输出作为待估模型，形成无位置传感器估算结构，其估算系统结构如图2所示。

2.2 估算自适应率推导

由式(1)可得，MRAS待估模型电流模型如下式[14-18]：

(2)

若设：

(3)

则用式(1)减去式(2)后可得：

(4)

若：

(5)

则式(4)可写成如下形式：

(6)

选取Lyapunov函数为如下形式：

(7)

由式(1)可知，反电动势信号中包含着电机转子的速度和位置信息，故而估算出反电势即可得出转子位置信息和转速根据电机反电势与转子位置的关系得出估算的位置信号：

若要使转子位置保持收敛，应具备前述Lyapunov稳定性理论的3个收敛条件

由式(7)可以看出，条件(1)和条件(3)已经满足了。仅对条件(2)，根据式(5)、式(6)，可得：

(8)

(9)

(10)

将式(8)、式(9)代入式(10)后，计算可得：

(11)

(12)

由于式(11)为负定矩阵，则eT(ATQ+QA)e一定为负定函数，此时若使：

(13)

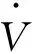
(14)

由式(14)可得反电势参数的α-β坐标系下自适应率分别：

(15)

(16)

Lyapunov稳定性理论保证了上述的参数电流待估模型以及推导的位置参数收敛算法稳定收敛。待估模型中位置量不断逼近PMSM转子位置，当位置估算系统稳定时，估算的转子位置即反映了电机的实际转子位置。

3 仿真验证

为了验证所提出MRAS位置估算算法的有效性，选用一台2 kW的永磁同步电动机，额定转速60 r/min,额定转矩300 N·m，极对数12，相电阻1.8 Ω，相电感12 mH,永磁体磁链0.65 Wb。仿真系统按照图1所示的矢量控制系统框图搭建。

图3为电机运行在30 r/min，负载转矩80 N·m下获得的波形。

(a) 估算反电动势波形

(b) 电机实际位置波形

(c) 电机估算位置波形

(d) 电机实际转速波形和估算转速波形图3 转速30 r/min,负载80 N·m的运行波形

由图3可以看出，在没有低通滤波器的情况下，使用模型参考自适应算法跟踪两相静止坐标系下的反电势波形的方法，得到了理想的反电势估算波形，估算的位置信号能够很好地跟踪实际位置信号，转速估算信号需要0.35 s才能够跟踪实际转速，这并不会影响系统的稳定运行。

为了进一步验证本文所提出的位置估算算法的性能，在0.5 s时，给定转速由30 r/min切换到60 r/min，负载转矩为80 N·m，仿真波形如图4所示。在50 r/min稳态运行时，在0.5 s时刻负载由0突加到300 N·m，仿真波形如图5所示。

由图4可以看出，MRAS算法在转速阶突变时能够对转子位置准确估算，转速也可以较快地跟踪到突变后的转速。

由图5可以看出，当电机负载突变时，位置估算所受影响较小，转速波形在负载突变时短时间内与实际转速变化趋势相反，但是最终都能收敛到实际值。上述的仿真验证表明，本文提出的MRAS算法在系统稳定前提下能够快速地跟踪转子位置和转子速度，当转速突变和负载突变时仍可保持快速跟踪性能。

(a) 反电动势估算波形

(b) 电机实测位置波形

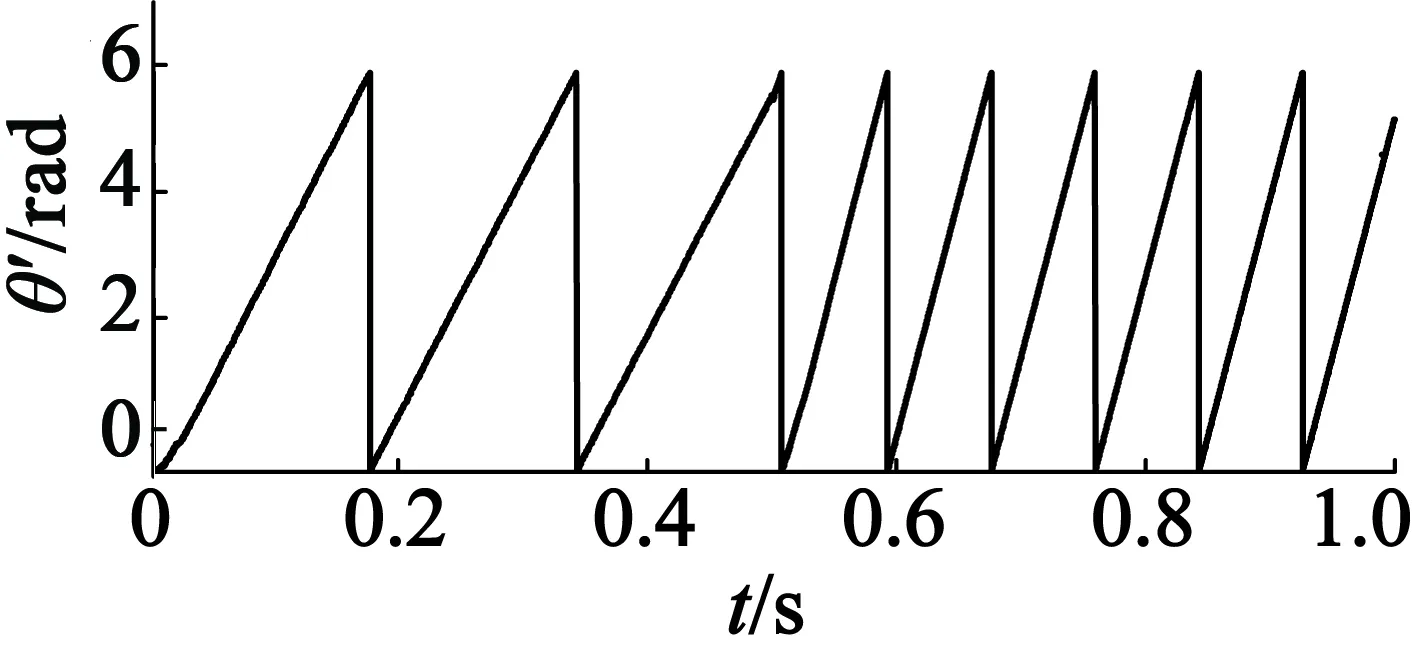
(c) 电机估算位置波形

(d) 电机实际转速波形和估算转速波形图4 转速由30 r/min到60 r/min的突变波形

(a) 电机实际位置

(b) 电机估算位置

(c) PMSM实际转速和估算转速

(d) 0.5 s附近负载突变时的转速变化图5 转速在50 r/min下，0.5 s时负载由 0阶跃变化至300 N·m的波形

4 实验验证

在上述仿真基础上，为验证该位置估算算法的实际效果，搭建基于MRAS无位置传感器估算的PMSM机矢量控制平台，驱动电路使用AD-DC-AC变频电路，三相逆变电路由智能控制单元IPM构成，选用一台2 kW PMSM作为位置估算对象，电机内部参数与仿真设置的相同，如表1所示，为验证算法准确性，利用增量式编码器对电机实际位置进行检测。

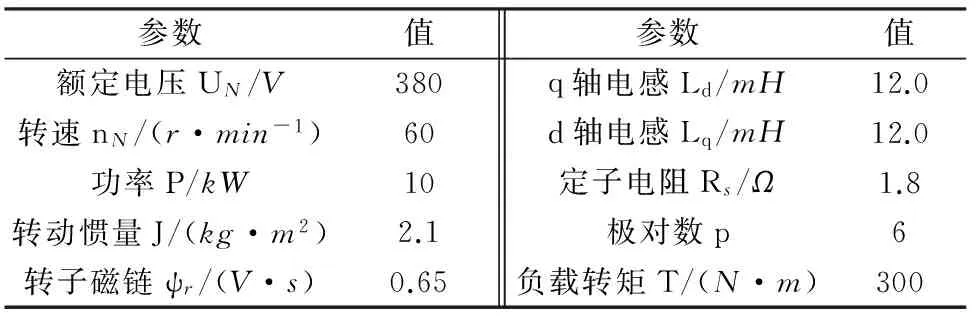
表1 电机内部参数表

由图6可知，该位置估算算法可以有效跟踪转子位置，估算位置波形与实测位置波形几乎重合，但估算位置波形存在一定的波动，这是由实际实验系统中的一些测量误差和噪声造成，同时，由图6的下半部分可知，估算转速可以有效地跟踪实际转速，但估算转速落后于实际转速，这是因为MRAS算法实际上是有差拍控制，存在一定的估算延时。

图6 转速30 r/min，负载转矩300 N·m下的转速 和位置估算波形与位置编码器实测波形对比

为进一步验证该位置估算算法的动态性能，图7给出了额定负载下，转速给定30r/min阶跃至60r/min时的转速和位置估算波形与位置编码器实测波形对比，由图7可知，当转速发生突变时，该算法可以有效地跟踪转速变化，很快地跟踪上实际的电机转速和位置变化。

5 结 语

本文将MRAS算法应用于PMSM的转子位置与速度估算中，利用Lyapunov稳定性理论，基于PMSMα-β坐标系下的电流模型，推导出了两相α-β坐标系下的反电势自适应收敛率，从而保证了位置估算系统的稳定性。再根据α-β坐标系下的反电势精确计算出了转子位置与速度，实现了PMSM机位置与转速的估算，并且具有较小的估算误差和较快的估算速度。仿真和实验验证了该算法的有效性和快速性。

[1] 梁艳，李永东．无传感器永磁同步电机矢量控制系统概述[J]．电气传动，2003，33(4)：4-9．

[2] 李永东，朱昊．永磁同步电机无速度传感器控制综述[J]．电气传动，2009,39(9)：3-10．

[3]CONSOLIA，SCARCELLAG，TESTAA．Industryapplicationofzero-speedsensorlesscontroltechniquesforPMsynchronousmotors[J]．IEEETransactionsonIndustryApplications，2001,37(2):513-521．

[4]UTKINV,GULDNERJ,SHIJingxin.Slidingmodecontrolinelectromechanicalsystems[M].BocaRaton,US:CRCPress,1999.

[5]UTKINVI．Slidingmodecontroldesignprinciplesandapplicationstoelectricdrives[J]．IEEETransactionsonIndustrialElectronics，1993，40(1)，23-36．

[6]CHENZ，TOMITAM，DOKIS，etal．Newadaptiveslidingobserversforposition-andvelocity-sensorlesscontrolsofbrushlessDCmotors[J]．IEEETransactionsonIndustrialElectronics，2000，47(3)：582-591．

[7]JIANGDong,ZHAOZhengming,WANGFei．AslidingmodeobserverforPMSMspeedandrotorpositionconsideringsaliency[C]//ProceedingsofIEEEConferenceonPowerElectronicsSpecialists.IEEE，2008:809-814．

[8]CHUJB，HUYW，HUANGWX．AnimprovedslidingmodeobserverforpositionsensorlessvectorcontroldriveofPMSM[C]//ProceedingsofIEEEConferenceonPowerElectronicsandMotionControl.IEEE,2009:1898-1902．

[9] 苏健勇，李铁才，杨贵杰．PMSM无位置传感器控制中数字滑模观测器抖振现象分析与抑制[J]．电工技术学报，2009，24(8)：58-64．

[10]PARASILITIF，PETRELLAR，TURSINIM．SensorlessspeedcontrolofaPMsynchronousmotorbasedonslidingmodeobserverandextendedKalmanfilter[C]//ProceedingsofIEEEConferenceonIndustryApplicationsConference.IEEE，2001:533-540．

[11]SONGC，ZHENGZ，XULY．Sliding-modesensorlesscontrolofdirect-drivePMsynchronousmotorsforwashingmachineapplications[J]．IEEETransactionsonIndustryApplications，2009，45(2)：582-590．

[12] 齐放，邓智泉，仇志坚，等．基于MRAS的永磁同步电机无速度传感器[J]．电工技术学报，2007，22(4)：53-58．

[13] 朱喜华，李颖晖，张敬．基于一种新型滑模观测器的永磁同步电机无传感器控制[J]．2010,38(13)：7-10．

[14] 齐放，邓智泉，仇志坚，等．一种永磁同步电机无速度传感器的矢量控制[J]．电工技术学报，2007,22(10)：30-34．

[15] 张承林，张复琳，王志福，等．无刷直流电动机无位置传感器控制技术综述[J]．微特电机，2014,42(2):70-74.

[16] 朱军，韩利利，汪旭东，等．永磁同步电机无传感器控制现状与发展趋势．微电机，2013,46(9):11-16．

[17] 鲁文其，胡育文，杜栩杨，等．永磁同步电机新型滑模观测器无传感器矢量控制调速系统[J]．中国电机工程学报，2010，30(33)：78-83．

[18] 丁文，梁得亮，罗战强，等．两级滤波滑模观测器的永磁同步电机无位置传感器控制[J]．电机与控制学报，2012,16(11):1-10．

[19] 王寅东．基于新型滑模观测器的永磁同步电机无位置传感器控制[D]．天津：天津大学，2012．

Position Sensorless Control of Permanent Magnet Synchronous Motor Drive System Based on MRAS

DENGPeng

(Jingchu University of Technology，Jingmen 448000，China)

In order to achieve the position sensorless control of permanent magnet synchronous motor (PMSM), a model reference adaptive system (MRAS) method which was based on the PMSM mathematical model inα-βreference frame was put forward. In this method, the PMSM position estimation model was established according to the Lyapunov stability theory, usingα-axis andβ-axis voltage, current, and their errors inα-βreference frame. The adaptive ratio of the positional parameter was deduced by means of Lyapunov stability theory, ensuring the stability of position estimation system and the convergence of error, and at the same time the position of PMSM rotor can be quickly and efficiently obtained. The simulation results show the reliability and effectiveness of this method.

permanent magnet synchronous motor (PMSM); model reference adaptive system (MRAS); position estimation

2015-11-01

TM341；TM351

A

1004-7018(2016)07-0051-05

邓鹏(1981-)，男，硕士研究生，讲师，研究方向为交流电机控制、电动车驱动控制、计算机控制等。