基于环结构分析的准循环LDPC码构造

李文雯，刘志伟，张炎林，刘丽丽，王 齐

(中国酒泉卫星发射中心，甘肃 酒泉 732750)



基于环结构分析的准循环LDPC码构造

李文雯，刘志伟，张炎林，刘丽丽，王 齐

(中国酒泉卫星发射中心，甘肃 酒泉 732750)

准循环奇偶校验(Quasi-Cyclic Low-Density Parity-Check， QC-LDPC)码在通信工程领域具有重要的应用价值，因此它的构造算法一直是LDPC码研究领域的一个热点内容。根据现有的QC-LDPC码构造算法，特别是基于渐进边增长(Progressive Edge Growth， PEG)算法的QC-LDPC码构造方法，提出了一种新的移位矩阵构造方法。该方法有效减少了随机搜索带来的时间损耗，并改进了二次同余、等差数列等算法仅能除去四环的情况，进一步消去了六环、八环和十环结构，确保QC-LDPC码的围长不小于12。仿真结果表明，所构造的QC-LDPC码具有更优的环结构特点和纠错性能。

准循环LDPC码；移位矩阵；围长；环结构

低密度奇偶校验(Low-Density Parity-Check，LDPC)码[1]是一类迫近香农限的“好码”，它具有较低译码复杂度、较强纠错性能以及较低的误码平层，在无线局域网、深空宇航、硬件存储、卫星数字电视等多个通信领域得到广泛的应用。准循环(Quasi-Cyclic，QC)LDPC码是一类典型的结构化LDPC码，它能够通过一组移位寄存器实现快速编码，并且具有校验矩阵存储空间小、能够进行并行译码、纠错性能良好等特点，因此在工程实践中得到了广泛的应用。在构造方法上，QC-LDPC码的构造方法主要可以分为基于有限几何的构造方法[2-3]和基于循环移位矩阵的构造方法[4-11]两大类。基于有限几何的构造方法致力于构造满足“行列约束”的基矩阵，从而有效确保QC-LDPC码的围长至少为6；但是该构造方法在码长和码率等参数的选择上缺少灵活性。基于循环移位矩阵的构造方法主要通过基矩阵和移位矩阵共同控制环的长度和数量。基矩阵在构造时主要以增大环长为目的，通常采用渐进边增长(Progressive Edge-Growth，PEG)算法[12]进行构造。在移位矩阵构造方面，文献[6]中采用随机搜索的方法，其优点在于能够通过重复搜索提高码的围长，但随机搜索的时间损耗和运算量会随着预设围长的增加而迅速增加。另一类移位矩阵的构造方法是采用二次同余[7]、等差数列[9]等算法，能够除去校验矩阵中所有的四环，即保证围长至少为6，但这种方法没有对六环及其以上的环结构做进一步的考虑。另一种采用等差数列构造移位矩阵的方法[11]虽然除去了六环，但需要固定校验矩阵的列重为3，对度分布的设计存在约束。

基于现有的研究成果，本文提出一种新的QC-LDPC码构造算法。该算法能够有效消除QC-LDPC码校验矩阵中长度小于12的短环结构，同时避免随机搜索带来的时间损耗和运算量。本文首先给出基于PEG算法的QC-LDPC码表示方法及环结构特点，随后在QC-LDPC码的特点及环结构分析基础上给出一类新的移位矩阵的构造方法，最后给出新构造的QC-LDPC码性能仿真结果并做出相应的分析和对比。

1 基于PEG算法的QC-LDPC码构造

QC-LDPC的校验矩阵由单位矩阵的循环移位矩阵和零矩阵组成，在结构上具有准循环移位特性。设mp×np阶矩阵H为QC-LDPC码校验矩阵，它在结构上可以表示为

(1)

其中：I(si，j)为p×p阶全零矩阵或者单位循环移位矩阵；si，j代表单位矩阵循环移位的次数，其中，1 ≤i≤m，1 ≤j≤n，-1≤si，j≤p-1。

根据校验矩阵H的结构，可以使用一个m×n阶的基矩阵B和一个m×n阶的移位矩阵P联合对其进行表述，从而降低矩阵表示及环结构分析的复杂度。基矩阵B用以表示相应位置上p×p子矩阵为全零矩阵还是单位矩阵的循环移位矩阵：移位矩阵P用以表示相应位置上p×p阶子矩阵循环移位的次数，即Pi，j=si，j。基矩阵B中的环称为块环，它决定了校验矩阵H环结构的框架；移位矩阵H中移位值的选取，在块环设定的框架下影响着校验矩阵H中环的长度和数量[6]。设基矩阵B中存在一个长为2t的块环，sαk,βk为该块环对应位置上的移位值(1≤k≤ 2t)，令

(2)

S1=Tmodp

(3)

则S1与H中的环长及数量存在以下关系[6]：

1)S1=0，则该长度为2t的块环在H中被“复制”为p个长度为2t的环；

2)S1≠0且S1与p互素((S1，p)=1)，则该长度为2t的块环在H中被“倍增”为1个长度为2tp的环；

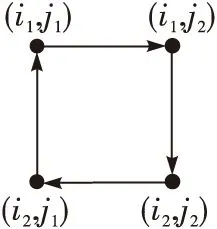
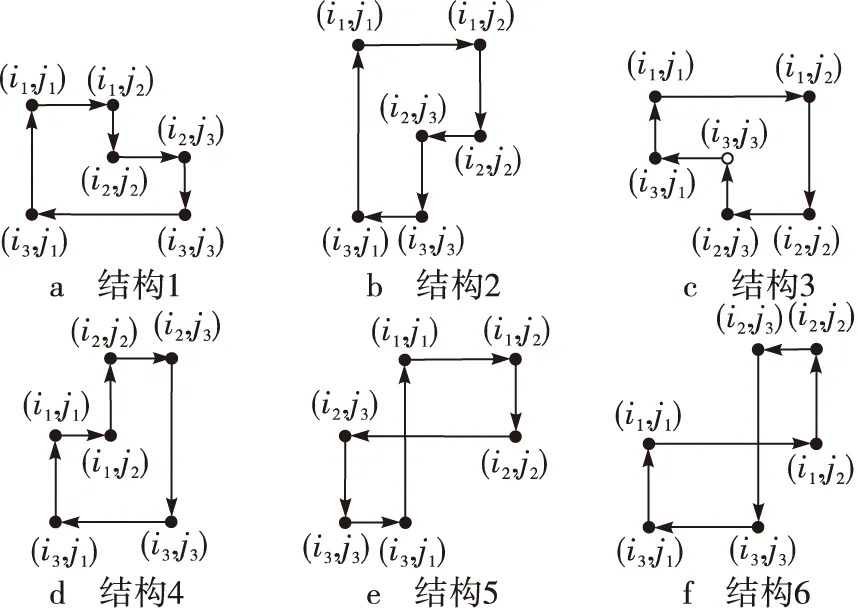
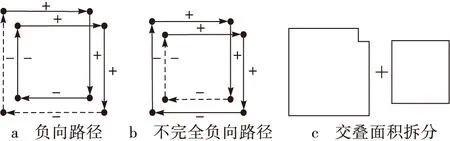
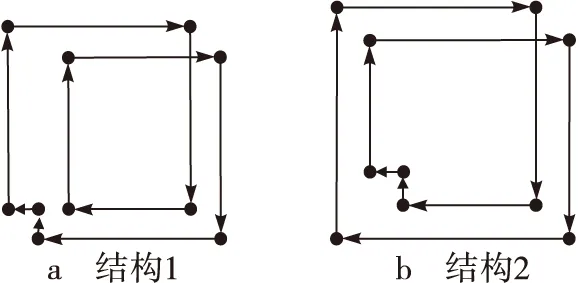
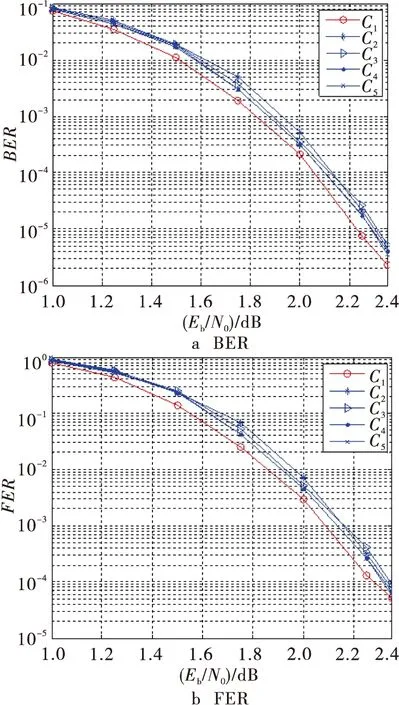
3)S1≠0但S1与p非互素((S1，p) ≠ 1)，则一定存在某个正整数l(1

lS1modp=0

(4)

该长度为2t的块环在H中扩展为p/l个长度为2tl的环。

由此可见，QC-LDPC码的环长由基矩阵中的块环和移位矩阵中相应位置上的移位值共同决定。若要增大QC-LDPC码的环长，则需要增大块环的长度并合理设置移位矩阵的移位值。在对基矩阵B进行构造时，采用现有相关研究中多使用的PEG算法[12]。它适合于低维度的校验矩阵构造，并以渐进边增长的方式最大限度地增大LDPC码围长，能够为QC-LDPC码提供理想的块环结构。在对移位矩阵P进行构造时，文献[6]中采用随机搜索的构造方法，需要对短环结构进行搜索，具有一定的运算复杂度和时间损耗；文献[7-9]中采用的方法虽然减省了环搜索的过程，但只能除去长度为4的短环。本文提出了一种新的移位矩阵构造方法，能够有效避免基矩阵中的环被“复制”的情况，使QC-LDPC码的围长至少为12。

2 移位矩阵的构造方法及环结构分析

由前文分析可知，在基矩阵相同的情况下，移位值的选取需要尽可能保证S1≠0，避免环结构被“复制”。 基于上述考虑，设基矩阵B和移位矩阵P的大小均为m×n，其中B由PEG算法构造得到，而P第i行第j列元素值设为

si,j=ij

(5)

其中:1≤i≤m，1≤j≤n，且(si，j)max=mn

2.1 块环长度为4

若基矩阵中存在一个四环结构，如图1所示。

图1 四环结构图

若si，j=ij，则

(6)

令j2-j1=a1，i2-i1=b1，则式(1)可以化简为

T=i1j1-i1j2+i2j2-i2j1=-i1a1+i2a1=a1b1

(7)

T恰好表示该环在矩阵中所围图形的面积。设该闭合图形的面积为S，则S>0且T=S。根据图形结构可知，四环所围图形的最大面积为(S)max=(T)max=(m-1)(n-1)

S1=Tmodp=T=S

(8)

由此可得

S1=S>0

(9)

2.2 块环长度为6

再考虑块环长度为6的情况。通常情况下，六环结构有6种，如图2所示。

图2 六环结构图

先以环结构(图2a)进行分析。若si，j=ij，则

i3j3-i3j1

(10)

令j2-j1=a1，j3-j2=a2，i2-i1=b1，i3-i2=b2，则式(3)可以化简为

T=i1j1-i1j2+i2j2-i2j1+i3j3-i3j1=-i1a1-

i2a2+i3(a1+a2)=a1(b1+b2)+a2b2

(11)

观察可知，T同样等于环结构图2a在基矩阵中所围图形的面积，即T=S。由于环结构图2b、图2c与图2d分别可由环结构图2a以90°，180°以及270°顺时针旋转获得，故分析过程与环结构图2a相同。同理，环结构图2f可由环结构图2e以180°顺时针旋转得到，因此以下仅对环结构图2e进行分析。根据图2e中的标识，当si，j=ij时，同样可得

i3j3-i3j1

(12)

令j2-j1=a1，j3-j2=a2，i2-i1=b1，i3-i2=b2，则式(5)可以化简为

T=i1j1-i1j2+i2j2-i2j1+i3j3-i3j1=-i1a1-

i2a2+i3(a1+a2)=a1(b1+b2)+a2b2

(13)

由图2e中的结构可以看出，i3-i2=b2<0，且b1+b2=i3-i1，故T同样等于环结构图2e在基矩阵中所围图形的面积。根据图形结构可知，六环所围图形的最大面积为(S)max=(T)max=(m-1)(n-1)-10。

根据前文分析，可以归纳出以下结论：若基矩阵中存在长为2t的环，移位矩阵第i行第j列元素值为si，j=ij，且aq=jq+1-jq，bq=iq+1-iq，其中1≤q≤t-1，则

(14)

2.3 块环长度为8

设块环从起点出发后，定义背离起点的路径为正向路径，用“+”表示；朝向起点的路径为负向路径，用“-”号表示。为形成一个闭合的环路，正、负路径必然同时存在于一个块环中。根据块环的结构，负向路径再分为两类：一类是始终向着起点行进，定义为完全负向路径，如图3a中加粗虚线所示；另一类是向着起点行进一段距离后又转为正向路径，定义为不完全负向路径，如图3b中加粗虚线所示。由图1和图2可知，长度为4和6的块环结构中不存在不完全负向路径。当块环长度增加到8时，不完全负向路径开始出现，如图3b中加粗虚线所示。不完全负向路径的产生会导致环所围成的图形交叠，在这种情况下图3b中的块环所围成的面积可以等效为图3c。

图3 负向路径的分类与交叠面积的计算

此时，T=S仍然成立，但S1与S间的相等关系不一定存在。当块环长度为8且存在不完全负向路径时，环所围成图形的最大面积，如图3a所示，则

Tmax=2(m-2)(n-2)+1

(15)

T与mn的大小关系未定，即存在m，n的取值，使得T>p。此时S1=Tmodp≠S，可能存在S1=Tmodp=0的情况，使得该长度为8的块环被“复制”。为了避免此类情况产生，加入以下附加条件

p>max{mn，2(m-2)(n-2)+1}

(16)

则S1=T0。

值得注意的是，校验矩阵中H的八环也可以通过四环的扩展得到。根据前文内容可知，当块环长度为4时，S1≠0但可能存在(S1，p)≠1，且使得lS1modp=0的l取值为2(即p=2S1)，此时该长度为4的块环被不完全扩展为p/2个长度为8的环，p必为一个偶数。为了避免这种情况的产生，更进一步规定p的取值为奇数。

2.4 块环长度为10

当块环长度为10时，最大的面积交叠为二重交叠。这是因为如果环的面积出现三重交叠时，图中必然会有3个多边形套接，块环长度至少为12。因此块环长度为10时，交叠的两个环分别为4环和6环，如图4所示。

图4 具有负向路径的长度为10的块环

对比图3a中长度为8的块环所围图形的面积可知，当块环长度为10时，有

Tmax=2(m-2)(n-2)

(17)

由于在2.3节中已经规定p>max{mn，2(m-2)(n-2)+1}且p为质数，因此在块环长度为10时同样有S1=T0成立。

综上，新移位矩阵构造方法可以概括为：若I(si，j)为非零子矩阵，则移位矩阵第i行第j列的元素为si，j=ij，其中1≤i≤m，1≤j≤n，p为一个大于max{mn，2(m-2)(n-2)+1}的奇数。

3 仿真结果与性能分析

仿真中将本文构造的QC-LDPC码分别与PEG算法构造的LDPC码以及随机搜索算法构造的QC-LDPC码进行对比，所有参与仿真的码均具有相同的结构参数：码长N=1 774，码率R=0.5，度分布λ(x)=0.5x2+0.5x3。码C1为采用本文构造方法构造的QC-LDPC码，其基矩阵和移位矩阵的行数m=7，列数n=14，扩展系数p=127，满足p>max{98，121}=121的要求；码C2为采用PEG算法构造的非结构化LDPC码；码C3，C4，C5为基矩阵与C1相同、移位矩阵均采用随机搜索算法构造的QC-LDPC码，围长分别为4，6，8，构造耗时分别为9 969 ms，69 748 ms，1.35×106ms，可见随机搜索算法的构造耗时随围长的增加而急剧增加。

在相同的条件下，对码C1～C5进行仿真并将它们的误帧率(Frame Error Rate， FER)和误码率(Bit Error Rate，BER)进行对比，结果如图5所示。仿真时采用加性高斯白噪声信道及二进制移相键控调制(Binary Phrase Shift Keying，BPSK)方式，译码算法采用传统的置信传播(Brief Propagation，BP)译码算法，最大迭代次数设置为100。

图5 QC-LDPC码C1～C5的性能对比

图5中的仿真结果表明，在相同的构造参数及仿真条件下，本文算法构造的QC-LDPC码性能优于PEG算法及随机搜索算法。如图5a所示，当BER=10-5时，码C1的性能优于C2～C5中性能最好的码C5约0.1 dB，证明C1具有更大的围长和更好的环结构特点。除了对于扩展系数p的取值存在约束条件，本文构造算法对度分布、码长、码率等参数没有提出要求，且在构造时不需要计算耗时，因此在应用上更具有灵活性。

4 结语

本文着眼于QC-LDPC码在工程实践中的广泛应用前景，在基于环结构分析的基础上给出一种新的QC-LDPC码构造算法。该构造算法通过一种全新的移位矩阵构造方法避免了对基矩阵中环结构“复制”的情况，有效增加了校验矩阵中的环长。相较于几种现有的QC-LDPC码构造方法，本文给出的构造方法具有以下两个显著特点：1)避免了随机搜索算法带来的搜索时间和计算量的损耗；2)进一步消除了长度为4，6，8和10环结构，有效增大校验矩阵的环长，使QC-LDPC码的围长至少为12。

[1]GALLAGER R G. Low-Density Parity-Check codes [D]. [S.l.]：MIT，1963.

[2]SONG S，LAN L，LIN S，et al. Construction of quasi-cyclic LDPC codes based on the primitive elements of finite fields [C]//Proc. Annual Conference on Information Science and Systems.[S.l.]：IEEE，2006：835-838.

[3]LAN L，ZENG L，TAI Y Y， et al. Construction of quasi-cyclic LDPC codes for AWGN and binary erasure channels： a finite field approach[C]// Proc. International Conference on Wireless Networks, Communications and Mobile Computing.[S.l.]:IEEE, 2005：146-151.

[4]FOSSORIER M P C. Quasi-cyclic low-density parity - check codes form circulant permutation matrices[J]. IEEE transactions inf. theory，2004，50：1788-1793.

[5]LI Z W，KUMAR B V K V. A class of good quasi-cyclic Low-Density Parity Check codes based on progressive edge growth graph. signals[C]// Proc. Thirty-Eighth Asilomar Conference on Systems and Computers.[S.l.]：IEEE，2004：1990-1994.

[6]雷菁，王建辉，唐朝京. 基于PEG算法的准循环扩展LDPC码构造[J]. 通信学报，2008，29(9)：103-110.

[7]HUANG C M，HUANG J F，YAN C C. Construction of quasi-cyclic LDPC codes from quadratic congruences[J]. IEEE communications letters，2008，12(4)：313-315.

[8]孔令军，赵莹，肖扬. 准循环LDPC码不存在四环的重要条件[J]. 铁道学报，2009，31(6)：39-45.

[9]郭锐，胡方宁，刘济林. 一种低差错平底线性复杂度的QC-LDPC码构造方法[J]. 电路与系统学报，2011，16(6)：87-93.

[10]刘星成，程浩辉. 基于PEG算法的准循LDPC码构造方法研究[J].电路与系统学报，2009，14(4)：115-119.

[11]张轶，达新宇，苏一栋. 利用等差数列构造大围长准循环低密度奇偶校验码[J].电子与信息学报，2015，37(2)：394-398.

[12]HU X Y，ELEFTHERIOU E，ARNOLD D M. Progressive edge-growth tanner graphs[C]// Proc. IEEE Global Telecommunications Conference. [S.l.]：IEEE，2001：995-1001.

责任编辑：闫雯雯

Construction of quasi-cyclic LDPC codes based on cycle analysis

LI Wenwen， LIU Zhiwei， ZHANG Yanlin， LIU Lili， WANG Qi

(JiuquanSatelliteLaunchCenterinChina，GansuJiuquan732750，China)

Quasi-cyclic Low-Density Parity-Check (QC-LDPC) codes have practical significance in the field of communication engineering， and their construction methods have always been a hot topic in the area of LDPC codes. Based on existing literature， especially those constructed through Progressive Edge Growth (PEG) algorithm， a new construction method for shift matrix is proposed in this paper. The method can efficiently reduce the time cost and computation caused by random search； eliminate short cycles with length 4，6，8 and 10 to guarantee the girth at least 12， which improves the error correction performance when compare with those methods based on quadratic congruence and arithmetic sequence. Simulation results show that the newly constructed QC-LDPC codes have good cycle structure and performance.

quasi-cyclic LDPC codes； shift matrix； girth； cycle structure

李文雯，刘志伟，张炎林，等. 基于环结构分析的准循环LDPC码构造[J].电视技术，2016，40(11)：95-99. LI W W，LIU Z W，ZHANG Y L，et al. Construction of quasi-cyclic LDPC codes based on cycle analysis[J]. Video engineering，2016，40(11):95-99.

TN911.2

A

10.16280/j.videoe.2016.11.020

2016-01-23