多径信道OFDM系统小数倍频偏估计算法改进研究

李 波，李 涛

(西安邮电大学 通信与信息工程学院，陕西 西安 710061)



多径信道OFDM系统小数倍频偏估计算法改进研究

李 波，李 涛

(西安邮电大学 通信与信息工程学院，陕西 西安 710061)

针对多径信道环境下OFDM系统小数倍频偏估计精度不足的问题，提出一种基于循环前缀(CP)估计的改进算法。该算法重点在于准确搜索出受到多径干扰的数据范围，利用未受到多径干扰的CP数据进行ML频偏估计，并对估计值加以修正，使得估计结果更加精确。仿真结果表明，改进算法相对于原算法具有更好的估计性能。

多径信道；OFDM；频偏估计；循环前缀

正交频分复用技术(OFDM)因其频带资源利用率高、抗频率选择性衰落效果好等优点，在无线通信领域中已受到了广泛应用。例如，数字视频广播系统(DVB-T)[1]、LTE系统[2]、基于IEEE802.11a的WLAN系统[3]。引起载波频率偏移(CFO)原因主要是收发终端混频载波精度不足、无线信道的非线性，以及多普勒效应等因素。对于OFDM系统，CFO会破坏各子载波间的正交性，严重影响系统性能，因此频偏估计的精度对于OFDM系统显得至关重要。频偏估计按照估计方法不同可分为基于辅助数据算法[4]和无辅助数据算法[5]，按照估计值范围的不同，CFO可以分为整数倍频率偏移(IFO)[6]和小数倍频率偏移(FFO)[7-9]。本文将讨论如何在多径信道下利用循环前缀(CP)准确地进行小数倍频率偏移估计。

插入CP可以有效地避免多径延时所引起的符号间干扰(ISI)，CP是无线应用中OFDM系统数据结构中不可缺少的组成部分。文献[5]提出基于CP、采用最大似然算法(ML)进行FFO估计，但是仅适用于平坦慢衰落的情况，在多径信道环境下估计值会存在较大误差。文献[7]针对在多径环境下利用ML进行估计，并对估计值进行相对误差分析，然后选取精度较高的估计值，该算法性能提升有限，在低信噪比情况下估计性能会严重恶化。

本文提出基于循环前缀计算在多径环境下的估计修正算法，算法假设最大延时长度小于循环前缀长度。通过对数据进行滤波处理，以加强抗高斯噪声干扰能力。

1 系统模型

在OFDM系统中，发送端和接收端分别依靠IFFT/FFT算法完成多载波正交调制和解调，所以OFDM系统对频偏非常敏感。但是由于本地混频载波精度存在误差，以及信号在传播过程中的多普勒效应，都会引起载波频率偏移，严重影响通信系统性能。其中OFDM系统框图如图1所示。

图1 OFDM系统框图

OFDM系统有N个子载波，经过IFFT调制后信号为d(n)，n∈{0,1,…,N-1}。每个符号前面都插入长度为NCP的CP，用来避免多径效应而引起的符号间干扰(ISI)。信号通过多径信道h(l)，其中假设多径最大延迟Tn小于循环前缀长度NCP。时域同步工作完成后，接收到的信号表达式为

n=0,1,…,N+Ncp-1

(1)

(2)

2 基于循环前缀的小数倍频偏估计

传统方法通过利用CP数据进行ML计算，得到小数倍频偏值，方法见式(3)。因为没有考虑多径信道对CP数据的干扰，直接利用全部CP数据进行相关运算，所以使得计算出的小偏值ε存在较大误差。

(3)

(4)

文献[10]提出利用未受到多径干扰的CP数据进行频偏估计的思想，即通过估计多径最大时延，求出受到多径干扰的CP范围，去掉干扰点，再利用剩余的CP数据进行相关运算，从而达到消除多径对于频偏估计影响的目的。

根据到达接收端的信号图2可知，由于多径，接收到的符号n受到上一个符号n-1的干扰。因为在各符号之间相位不连续存在相位翻转现象，所以G1与G1′相关性降低。在这里，设定多径的最大时延Tn小于循环前缀长度NCP，所以G2区间并没有受到多径时延的影响，因而G2与G2′仍然保持良好的相关性。根据上述结论，可以利用区间的相关性计算出最大多径时延Tn，确定G2区间的起始位置，然后依据G2区间的CP数据来计算频偏值，证明见式(5)。

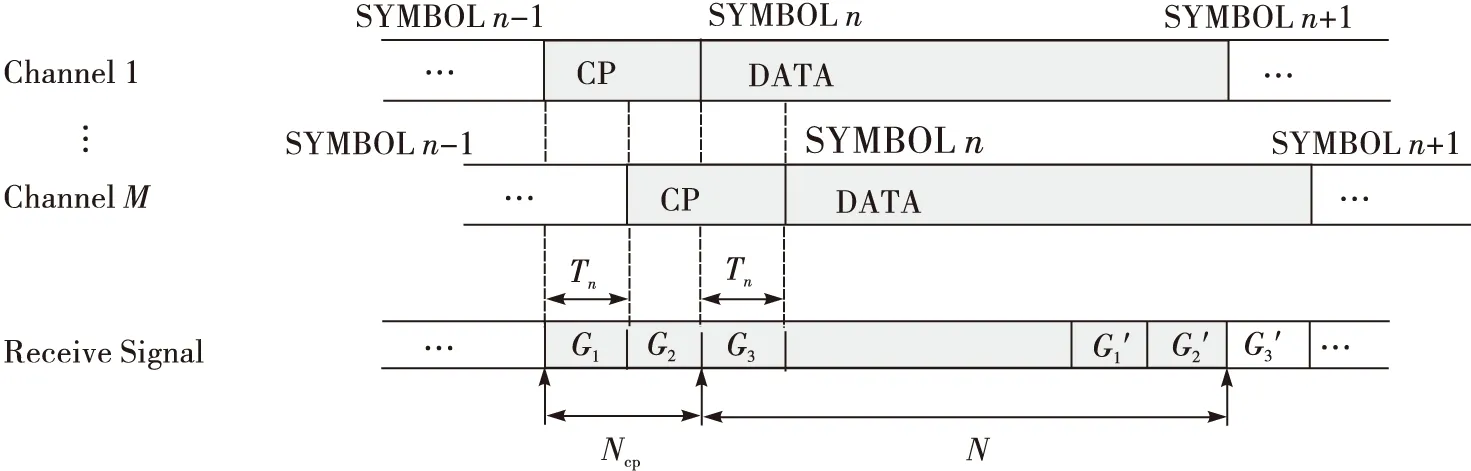
图2 多径延时环境下OFDM符号结构

(5)

(6)

(7)

(8)

(9)

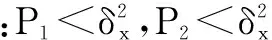
(10)

式中：λ∈{G1∪G2}，θ用来搜索区间G2的起始位置。由上面的结论可知，当λ在G1区间内，θ值会随着λ的增大而增大。当λ在G2区间内时，θ值将达到最大值并且维持不变。由此可知，若λ取λopt时，θ达到最大值，则λopt为多径的最大延迟的采样点。根据计算出的λopt位置，去掉受到多径延迟干扰的CP，利用剩余的CP数据计算频偏值。

(11)

(12)

(13)

该算法极大地改善了由多径引起的频偏值估计精度不足的问题，但是在实际应用中，由于发送数据具有随机性，以及高斯噪声的存在，通过相关运算得到的θ值会出现波动现象，因而搜索θmax会出现无法准确定位λopt问题。本文借用一种数据光滑处理方法，进而改善这个问题。

文献[11]提到的Savitzky-Golay光滑滤波算法，该算法利用一定长度的滤波器和待处理数据进行卷积，对待处理数据作多项式拟合，通过拟合，得到最小均方根误差，而偏离大部分的点将不参与计算，从而达到平滑滤波的目的。

针对λopt定位不准的问题，采取光滑滤波后效果见图3。观察可知，经光滑滤波后，在G1区间θ值是单调递增的，在G2区间θ值基本趋于稳定。由此通过对光滑滤波后的数据进行单调性判断，找到合适的λopt点。判断流程如图4所示。

图3 Savitzky-Golay光滑滤波效果图

图4 搜索λopt流程图

除去干扰，剩余的CP数据，可以较精确地估计出频偏值。在实际数字无线通信系统中，混频模块、AD/DA转换模块等是必不可少的。由于各模块受到温度、电磁干扰等因素影响，难免会存在突发干扰。同样ML算法本质通过相关运算得到的复数求出角度，计算结果对复数的实部和虚部的数值大小比较敏感，运算过程对数据的量化会产生一定误差，因此也会产生估计结果大幅度偏离平均值的现象，如图5所示。

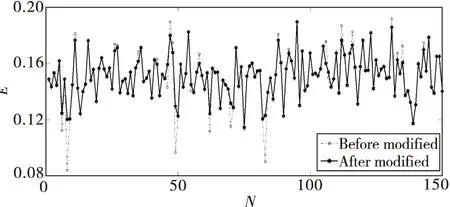
图5 消除突发干扰效果图

对于此问题，采用数据聚类思想滤除这些突发干扰。具体方法步骤为：

1)计算末尾L个数据的平均值aver，以此平均值为质心。设定取值半径R。

2)在0≤n

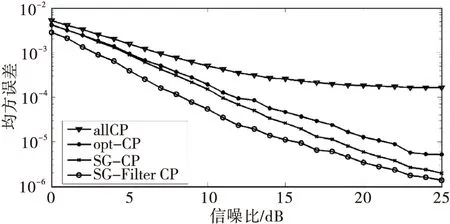
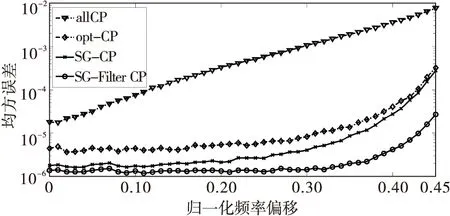
3 仿真结果

使用MATLAB对上述算法进行仿真，仿真中假设接收端已完成时域同步工作。其中，仿真信号数据参数为：OFDM符号长度N为2 048，CP长度NCP为512，信号带宽5 MHz，载波频率为320 MHz。仿真多径信道有4条多径，时延分别为[0，3，6，12] μs，每条径的功率为[0，-2，-5，-7]。设定归一化频偏值ε为0.15。估计值的均方误差与信噪比关系曲线如图6所示。由图可知，基于CP的ML算法会受到信噪比的影响,随着信噪比的增大，估计精度会增加。本文提出的算法的到的估计值，在各个信噪比情况下，估计精度都优于另外3种算法。

图6 ε取0.15时均方误差与信噪比关系图

图7给出当信噪比为25 dB时，均方误差与各归一化频偏值的曲线关系。本文提出的算法估计精度在各频偏值情况下优于另外3种算法。但是由于基于CP的ML估计算法估计范围为[-0.5，0.5]。当归一化频偏值靠近范围边界时，容易出现极性反转。因而，当归一化频偏值靠近边界时，均方误差值增大。

图7 信噪比取25 dB时均方误差与归一化频偏值关系图

4 结论

针对多径信道中的OFDM系统，本文提出了基于CP数据进行小数倍频偏值估计的优化算法。本算法可以有效计算出受到多径延迟干扰的CP数据位置，并给出估计值误差的一种修正方法。

[1]方绍,谢显中.基于DVB-T的OFDM频偏估计算法及DSP实现[J].电视技术，2011，35(3)：5-8.

[2]CAPOZZI F,PIRO G,GRIECO L A, et al. Downlink packet scheduling in LTE cellular networks: key design issues and a survey[J].IEEE communications surveys & tutorials, 2012,15(2):678-700.

[3]崔丽珍,孙瑞漩.基于IEEE 802.11a的OFDM系统信道估计算法研究及实现[J].电视技术,2012,36(15):97-100.

[4]TANG Y,ZHENG F,LIU H,et al. A data aided estimation algorithm of decimal frequency offset for OFDM system[J].Advanced materials research,2014(902):385-391.

[5]JAN-JAAP V D B,SANDELL M, BORJESSON P O.ML estimation of time and frequency offset in OFDM systems[J]. IEEE transactions on signal processing,1997,45(7):1800-1805.

[6]LI D,LI Y,ZHANG H,et al. Integer frequency offset estimation for OFDM systems with residual timing offset over frequency selective fading channels[J].IEEE transactions on vehicular technology,2012,61(6):2848-2853.

[7]廖腾达,谢显中,郑品莲.基于循环前缀的LTE系统多普勒频偏估计算法[J].电视技术，2010,34(1)：56-58.

[8]MA S,PAN X,YANG G H,et al. Blind symbol synchronization based on cyclic prefix for OFDM systems[J].IEEE transactions on vehicular technology,2009,58(4):1746-1751.

[9]孙宇明,张彦仲,邵定蓉,等.基于噪声判决的OFDM小数倍频偏估计算法[J].通信学报,2010,31(8):56-62.

[10]LIU M,LI B,GE J. Blind estimation for OFDM fractional frequency offset over multipath channels[J]. Wireless personal communications,2014,79(1):119-130.

[11]周增光,唐婷.基于质量权重的Savitzky-Golay时间序列滤波方法[J].遥感技术与应用,2013,28(2):232-239.

李 波(1980— )，硕士生导师，主研无线通信系统设计、通信信息处理等；

李 涛(1991— )，硕士生，主研宽带无线通信。

责任编辑：薛 京

Modified algorithm for OFDM fractional frequency offset over multipath channels

LI Bo, LI Tao

(SchoolofCommunicationandInformationEngineering,Xi’anUniversityofPostsandTelecommunications,Xi’an710061,China)

For the insufficient accuracy of fractional frequency offset estimation in OFDM system, a modified algorithm based on cyclic prefix (CP) is proposed. This algorithm emphasizes on how to search the range of the interferential data from multipath channels, and uses pure CP to estimate frequency offset, in order to make the results more accurate and the estimated results corrected. The simulation results show that modified algorithm has better estimation performance.

multipath channels; OFDM; frequency offset estimation; cyclic prefix

李波，李涛.多径信道OFDM系统小数倍频偏估计算法改进研究[J]. 电视技术，2016,40(11)：81-84. LI B, LI T. Modified algorithm for OFDM fractional frequency offset over multipath channels[J]. Video engineering，2016,40(11)：81-84.

TN929.5

A

10.16280/j.videoe.2016.11.017

陕西省科技统筹创新工程计划项目(2011KTCL01-10)

2016-03-25