西湖凹陷致密低渗砂岩测井解释模型

李钧轲，李德勇

（中国海洋大学海洋地球科学学院，山东青岛266100）

西湖凹陷致密低渗砂岩测井解释模型

李钧轲*，李德勇

（中国海洋大学海洋地球科学学院，山东青岛266100）

在岩石结构复杂的低孔渗储层中，如何根据已有的岩芯、测井等资料来更加精确地求取储层物性参数是十分重要也十分困难的。不同工区的地质特征、流体性质、储集特征各不相同，因此也应对不同的测井解释模型。在借鉴前人研究的基础上，根据本工区的岩芯、测井资料，利用交会图和直方图技术建立了针对本工区的储层测井解释模型，提高了本工区低孔渗储层的测井解释精度，为后期勘探开发工作提供了崭新思路和可靠依据。

西湖凹陷；测井解释模型；孔隙度；渗透率；含水饱和度

西湖凹陷位于东海盆地陆架边缘，是东海盆地中面积最大、勘探程度最高的沉积凹陷，呈北北东—北东走向，南北长约420km，东西宽约100km，面积约4.27× 104km2。西湖凹陷自老到新发育有古新统、下始新统、中上始新统（平湖组）、渐新统（花港组段）、中新统（龙井组、玉泉组和柳浪组）、上新统（三潭组）及第四系（东海群）。其中，龙井组、花港组、平湖组地层为西湖凹陷勘探的目的层，而花港组是本文研究的重点地层。花港组主要发育于浙东坳陷，厚1000～2000m。

1 概述

储层测井解释的主要任务是将自然伽马、纵横波声波时差、电阻率、密度、自然电位等测井曲线依据不同的地质特征选取合适的解释模型，计算成泥质含量、孔隙度、渗透率、含水饱和度等物性参数。最后，根据这些地质参数，研究储层及其岩性、物性和含油性，包括储油性能、渗滤特性、流体性质及产烃能力，以便对地下地质情况、产层特征、油气层分布与生产能力做出全面评价及符合地下原貌的模拟，从而在宏观上显示出较高的精度和较好的经济效益[1]。为了提高储层测井解释模型的计算精度，在针对此工区进行储层测井解释模型时，对关键井储层岩芯基本资料进行分析并进行岩芯归位等处理。对该工区测井资料进行环境校正、深度校正、滤波处理、标准化及归一化处理，最终建立该工区精确的储层测井解释模型。

2 测井解释模型

2.1 地层泥质含量

地层泥质含量是评价储层物性及岩性的一个重要参数，是由各种细粉砂、粘土矿物、直径小于0.01mm的非粘土矿物细颗粒组成的复杂混合物。因此准确计算地层泥质含量是一个必要和复杂的问题[2]。此次工区研究层位为含泥质砂岩，通过对比前人研究成果并结合西湖凹陷地区储层特征，认为自然伽马测井能较好地反映地层泥质含量，因此选取自然伽马测井曲线（GR）计算地层泥质含量（Vsh）。

在实际计算过程中，采取（1）、（2）式计算泥质含量。

式中：GR——自然伽马测井值，API；

SH——曲线相对值，又称泥质含量指数，若SH≤0,SH=0.001，若SH≥1,SH=1；

Gmin——纯砂岩的自然伽马测井值，API；

Gmax——纯泥页岩的自然伽马测井值，API；

GCUR——地层年代系数,第三系以下老地层取2，新地层取3.7，花港组为新地层，故选择为3.7。

X1井、X2井自然伽马曲线计算地层泥质含量图如图1、图2所示。

图1、图2分别为X1井、X2井利用自然伽马曲线计算地层泥质含量的归一化数值。X1井选取3650～4050m共400m储层进行示意，X2井选取3200～3600m共400m储层进行示意。从图中可以看到，自然伽马曲线与地层泥质含量具有良好的正相关性，即自然伽马曲线数值较高处地层泥质含量也较高。利用所计算地层泥质含量可以精确划分储层并有效评价储层的性质和质量。

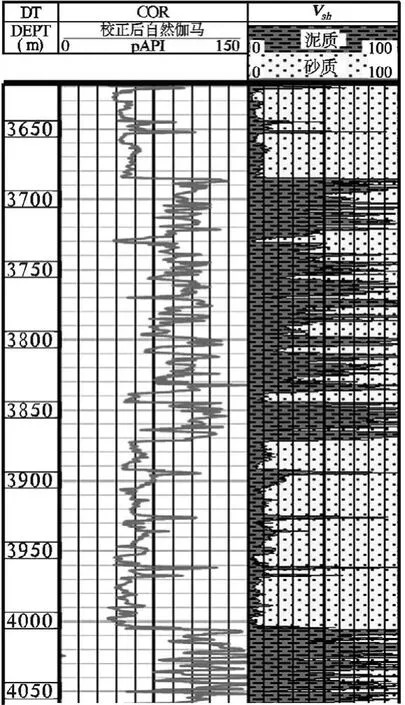
图1 X1井自然伽马曲线计算地层泥质含量图

图2 X2井自然伽马曲线计算地层泥质含量图

2.2 孔隙度解释模型

孔隙度是反映储层物性的重要参数，也是储量、产能计算及测井解释不可缺少的参数之一[3]。由于孔隙度曲线的测井地质基础及测井机理不尽相同，孔隙度曲线纵横向分辨率受井眼及储层流体性质等非孔隙性因素的影响程度有较大差异[4]。

此项工作利用实验室进行岩芯分析资料所得到的孔隙度与测井所得到的纵波声波时差—密度曲线进行回归分析。将岩芯归位后的孔隙度与纵波声波时差—密度交会，得到交会图及二元一次回归方程：

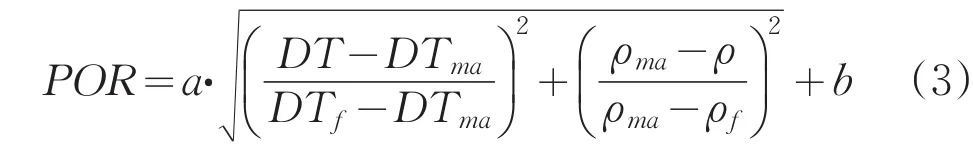
式中：DTma——目的层声波时差值，55.47μs/ft；

DTf--岩石骨架声波时差值，188.98μs/ft；

DT——流体时差值，μs/ft；

ρ——目的层密度值，g/cm3；

ρma——岩石骨架密度值，2.65g/cm3；

ρf——流体密度值，1.0g/cm3。

岩芯分析所得孔隙度与纵波声波时差—密度交会图如图3、图4所示。

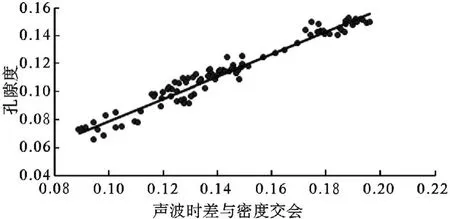
图3 X1井声波时差与密度交会法

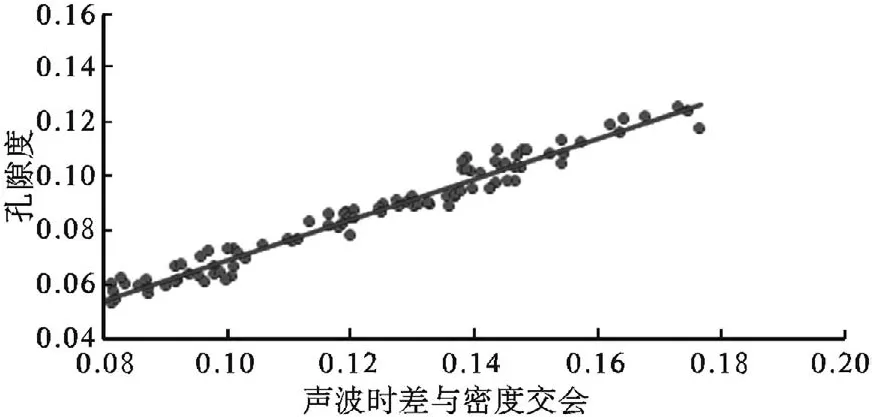
图4 X2井声波时差与密度交会法

图3、图4是利用西湖凹陷某区块X1、X2井的经过岩芯归位、标准化处理、归一化处理的某层位的纵波声波时差DT、密度RHOB与实验室岩芯分析得到的孔隙度POR进行交会得到的关系图，得到的回归方程为：

POR=0.7945×

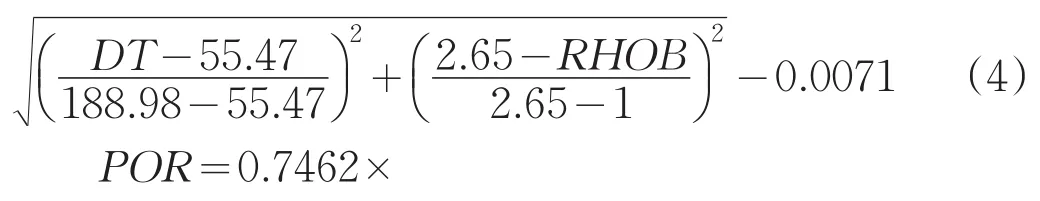
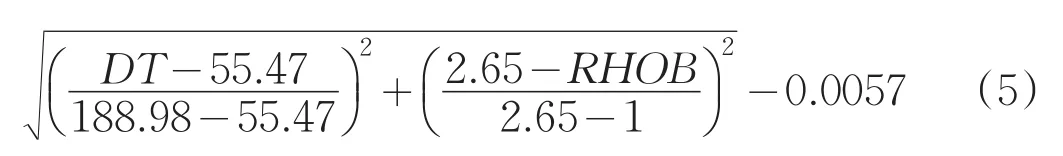
相关系数分别为R2=0.9557、R2=0.9684，一般认为相关系数R2＞0.8即为此关系式可信度较高，因为此关系式可信。

西湖凹陷某区块储层岩石结构复杂，利用测井资料直接计算孔隙度有一定的困难。经综合分析可以看出，若条件允许可利用多条曲线计算孔隙度时，在该工区优先选取纵波声波时差—密度曲线进行孔隙度计算。

2.3 渗透率解释模型

岩石的渗透率是指岩层在一定的压差下允许流体通过的能力，它是评价油层好坏的重要指标之一，确定岩层渗透率是测井资料定量解释的重要任务之一[5]。而渗透率的大小由储层孔隙度的大小以及孔隙结构特征共同决定，且储层孔隙的几何形态和大小也会影响渗透率。由于孔隙度与渗透率一般呈正相关性，因此实际工作中常常利用孔隙度采取统计方法计算渗透率。

对于西湖凹陷某区块低孔低渗的储层特征，经分析得知孔隙度与渗透率相关性较好，因此利用孔隙度为自变量与渗透率做交会图并求取进行回归方程。此项工作利用实验室进行岩芯分析资料所得到的孔隙度与渗透率进行回归分析，做孔隙度与渗透率交会图并得到指数函数：

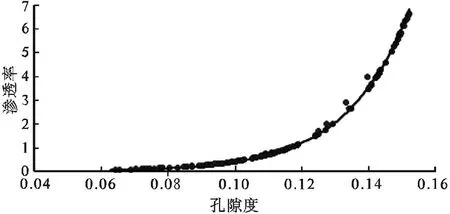
岩芯分析所得孔隙度与渗透率交会图如图5、图6所示。

图5、图6是利用西湖凹陷某区块X1、X2井的经过实验室岩芯分析得到的孔隙度POR与渗透率PERM进行交会得到的关系图，得到的回归方程为：

相关系数分别为R2=0.9984、R2=0.9972，一般认为相关系数R2＞0.8即为此关系式可信度较高，因为此关系式可信。

2.4 含水饱和度解释模型

含水饱和度Sw和含气饱和度Sg是评价储层含气性的主要标志。由于目前西湖凹陷某区块无岩芯分析含气饱和度数据，因此通过研究储层的含水饱和度来实现。含水饱和度是水的体积在储层岩石的孔隙的体积中所占的比例，是评价储层的一个基本参数。

考虑泥质对岩石电阻率的影响,1983年法国Si⁃mandoux对砂和粘土组成的人工介质做了广泛的实验研究,得出泥质砂岩电导率关系式：

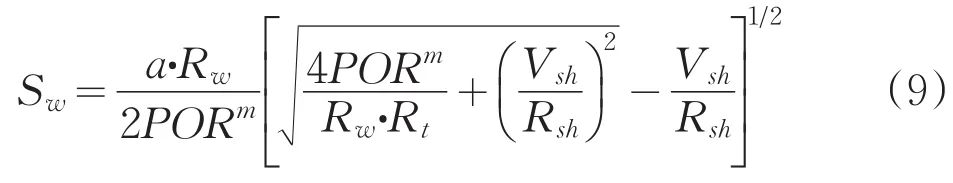
该式是混合泥质砂岩模型，是一种反映含分散泥质的岩石导电性模型[7]。其中Vsh为泥质含量，Rsh为泥质电阻率。Simandoux公式在实际应用中不考虑泥质和粘土的具体分散形式，并认为泥质和纯砂岩一样含有水和气，这与实际情况较为吻合，这样也能够消除储层物性差异所带来的影响。在实际计算含水饱和度过程中，岩性系数b和饱和度指数n变化范围较大，Si⁃mandoux公式没有采用这两个参数，减少了可能出现的误差。

因此，针对西湖凹陷某区块的低孔低渗储层以及泥质含量较高的的地质条件，采用Simandoux公式计算含水饱和度的准确略更高。

3 测井解释模型检验

测井解释成果图如图7所示。

从左至右分别为泥质含量、孔隙度、渗透率、含水饱和度，其中渗透率用对数方式显示，其余采用百分比形式显示。从图中显示看出，所计算的测井解释模型与实测数据及地下真是情况基本对应一致。

4 结论

应用所建立的测井解释模型，对西湖凹陷某区块的测井资料进行了处理和解释，为此工区储层评价提供了地质依据和油藏描述的基础。根据岩芯分析资料、地质资料、测井资料建立了较为精确的测井解释模型，有效提高了西湖凹陷某区块低孔渗储层的解释准确率，为下一步的勘探开发提供了可靠的依据。

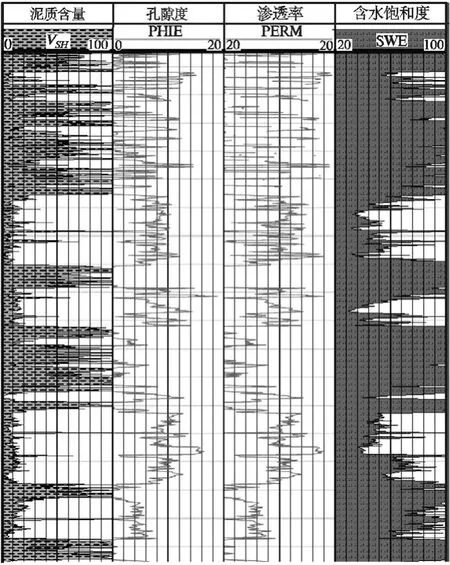
图7 测井解释成果图

[1]曹嘉酋，刘士安，高敏.测井资料综合解释[M].北京：石油工业出版社，2002.

[2]尚作源，欧阳健.测井新技术与油气层评价进展[M].北京：石油工业出版社，1998.

[3]黎文清.油气田开发地质基础[M].北京：石油工业出版社，1993.

[4]洪斌.苏里格气田苏X区块测井储层评价[D].成都理工大学硕士学位论文，2009：26-35.

[5]王会丽.金湖凹陷低孔低渗储层分布与测井评价方法研究[D].中国石油大学硕士学位论文，2011：27-42.

[6]张海涛.苏格里地区有效储层测井识别方法研究[D].西北大学博士学位论文，2010：67-73.

[7]雍世和，张超谟.测井数据处理与综合解释[M].东营:石油大学出版社,1996.

[8]林承焰.乐安油田草4块Es4稠油油藏测井解释模型研究[J].西南石油大学学报，2008，30（4）：2-5.

[9]胡杨，等.大牛地气田测井解释模型建立与气层识别标准研究［J］.石油地质与工程，2008，22（3）：37-41.

[10]孙建孟.应用岩心分析资料建立测井解释模型［J］.石油大学学报：自然科学版，1995，19（4）：28-34.

TN929.5

A

1004-5716(2016)12-0008-04

2016-01-25

2016-01-26

李钧轲（1990-），男（汉族），天津人，中国海洋大学读硕士研究生，研究方向：油气田与煤田地球物理勘探。