平行轴圆柱副接触分析

田红亮,陈甜敏,郑金华,余媛,张屹,赵春华

(三峡大学机械与动力学院,443002,湖北宜昌)



平行轴圆柱副接触分析

田红亮,陈甜敏,郑金华,余媛,张屹,赵春华

(三峡大学机械与动力学院,443002,湖北宜昌)

将古典赫兹理论与现代Majumdar-Bhushan模型相结合,建立了两圆柱分形接触模型。考虑结合部虚拟材料厚度,以及引入圆柱接触面积比,对两圆柱线高副矩形接触面进行了受力分析。数值仿真表明:圆柱接触面积比不大于1;外接触时圆柱接触面积比小于内接触时;增加总载荷或减小结合部虚拟材料厚度都将增大圆柱接触面积比;外接触时实际接触面积小于内接触时;实际接触面积随着分形粗糙度、材料硬度或结合部虚拟材料厚度的增加而减小;随着分形粗糙度的增加,产生特定实际接触面积所需要的总载荷增加,微凸体变形量增大;对于给定总载荷,当分形维数从1.4增加到1.5时,实际接触面积相应增大,但当分形维数从1.5增加到1.9时,实际接触面积转而减小;内接触时的赫兹应力小于外接触时的赫兹应力。该研究结果可为进一步研究圆柱齿轮传动的齿面接触疲劳强度计算提供参考。

机械设计;结合部;分形接触;虚拟材料;圆柱;线高副

机械系统中各零件之间力的传递总是通过两零件的接触来实现的。当前描述、表达与分析两接触物体接触行为的2种主要解算方法,一种是侧重考虑两接触物体宏观因素的古典赫兹理论[1],另一种是重点考察两接触物体微观因素的现代Majumdar-Bhushan模型[2](以下简称MB模型)。

古典赫兹理论采用弹性力学,考虑两接触物体的宏观因素(如零件初始接触线处的曲率半径,球或圆柱的曲面形状,外接触或内接触的接触方式),可以给出线接触时的接触压应力计算公式。接触压应力是机械零件接触疲劳强度计算的基础应力,古典赫兹理论首先解决了接触压应力计算问题,但却没有考虑两接触物体的微观因素(如接触表面处的微观几何学形貌,表面粗糙度)对接触压应力的影响,不能精确计算精密测试仪器的接触压应力。

MB模型依据分形理论,计及了两接触物体的微观因素(如接触表面处的微观几何学形貌,分形维数D,分形粗糙度G),能够推导出两粗糙平面接触时的总法向接触载荷、实际接触面积的计算公式,但MB模型没有考虑两接触物体的宏观因素(如零件初始接触线处的曲率半径,曲面形状,接触方式)对实际接触面积的影响,也不能准确计算两曲面接触后的实际接触面积。目前尚未见到从理论上精准计算两粗糙曲面接触时实际接触面积的文献。

机械加工工艺路线(如金属的冷加工、热加工、普通热处理、表面热处理、粗机械加工、精机械加工)、材料属性(如弹性模量、泊松比、交货状态布氏硬度HB、最初屈服强度σy)及所受外载荷均相同的零部件互相接触时,如果零部件的微观几何学形貌、表面粗糙度、曲面弧的弯曲程度(用曲率度量)与接触方式相异,则零部件的弹塑性变形与两零件间接触受力后的压应力亦皆相异。假如完全根据古典赫兹理论研究接触问题,就无法区别微观几何学形貌与表面粗糙度相异的情况。假设纯粹按照MB模型探讨接触问题,同样不能区别曲面弧弯曲程度和接触方式不同的情况。

早在1881年,赫兹首先用数学和弹性力学方法推导出了点接触问题的计算公式。1882年,为解决线接触问题,赫兹发表了经典论文《论弹性固体的接触》,随后通过实验验证了他的理论公式的正确性,从而开创了接触力学这门学科。此后,人们从宏观到微观、从现象到本质,通过理论分析和试验测试,对机床系统中各种典型结合部的作用机理进行了大量研究,并取得了相应的研究成果。Majumdar等利用Weierstrass-Mandelbrot分形函数,提出了具有尺度独立性的粗糙表面弹塑性接触分形模型,通过描述粗糙表面的2个重要表征参数和一些工程参数,推导出了法向载荷的表达式[3],但是没有考虑切向接触,忽略了弹、塑性转变带来的加工硬化,硬度随表面深度的变化,以及变形微凸体间的摩擦力。针对MB模型中最大弹性微接触点的面积偏大的不足,Wang等做了相应的改进:第一,提出了扩展分形函数;第二,区分了实际微接触面积与微接触截面积,给出了它们之间的关系式,通过定义一个扩展非零域、一个域扩展系数和一个域分开系数,求得了更为合理的微接触扩展概率分布密度[4-7]。Horng建立了椭圆抛物面微凸体弹塑性接触模型,推导出了弹性接触面积、弹性接触载荷、塑性接触面积、塑性接触载荷与干涉量、椭圆离心率的通用关系,以及临界干涉量、塑性指数与椭圆离心率、椭圆平均有效半径、椭圆等效半径的关系[8]。但是,上述文献[2-8]都有一个共同的问题,即均为主要针对两平面接触表面的载荷承载分析,而对于不同形状的曲面接触体的载荷,则不能正确分析。

古典赫兹理论与MB模型各有优、缺点,二者可以互补。本文对两圆柱线高副接触时形成的矩形接触区域进行受力分析,在分析过程中,试图把古典赫兹理论与MB模型相结合,将两平面接触推广到两圆柱曲面接触,使所建立的模型更具通用性与实用性。

1 两圆柱接触受力后的实际接触面积

2个轴线平行的圆柱作外或内接触,圆柱的初始接触线长度为b。受力前,两圆柱沿与轴线相平行的一条线相接触。受力后,作用在轴向长度b上的径向压缩均匀分布总载荷为F,则作用在单位轴向长度上的压缩载荷(称为载荷集度)为

q=F/b

(1)

受力后,因为材料发生了弹性变形,接触线变成宽度为2a、长度为b的一个矩形面。半接触宽度a的表达式[9]为

(2)

式中:E为综合弹性模量,r为综合曲率半径,并且满足

(3)

(4)

其中E1、E2分别为小圆柱和大圆柱材料的弹性模量,μ1、μ2分别为小圆柱和大圆柱材料的泊松比,r1、r2分别为小圆柱、大圆柱初始接触线处的曲率半径,±表示接触方式,正号用于外接触,负号用于内接触。

上述矩形面的面积即为实际接触面积,计算公式为

Ar=b2a

(5)

将式(2)代入式(5)得

(6)

将式(1)代入式(6)得

(7)

将式(4)代入式(6)得

(8)

2 圆柱接触面积比

圆柱表面包括圆柱面、顶面和底面。两圆柱面的面积和差为

MΣ=M2±M1=2π(r2±r1)b

(9)

式中:M1、M2分别为小圆柱面和大圆柱面的面积。

Mandelbrot在研究地球表面的几何形貌时发现,面积A超过一定值a的海洋面上的岛屿数N与a之间满足幂律关系[10]

N(A>a)～a-D/2

(10)

式中:符号“～”表示正比。

在MB模型中,岛屿数

(11)

式中:aL为最大岛屿的面积。

接触点的概率分布密度为

(12)

文献[10]指出:在MB分形模型中,n(a)的求解需要假设两接触体在无限平面里接触,或相对各个微突体来说为无限接触。很显然,当接触的2个曲面为非无限接触时,接触时所形成的接触点的总数N将有所变化。假设随着接触面的增大,两接触体的接触点数会增加,但其值小于或等于a-D/2(正确的表达式应为(aL/a)D/2,由式(10)与式(11)知文献[10]将符号“～”等同于符号“=”)。因此,两接触体的理论接触面积对N的大小有影响。

当两曲面完全内接触时,为式(11)所描述的情况。当两曲面一般接触时,N满足

(13)

式中:λ为圆柱接触面积比。可见,式(13)与文献[10]中的式(4)——N(A>a)=λa-D/2不同。

文献[10]认为,由于接触数N是指数函数形式(正确的说法应为幂函数形式,因为由式(12)知a是变量),因此设λ亦为指数函数形式(正确的说法亦应为幂函数形式)。多数文献都假定结合部的质量为0,即结合部的厚度为0,但是结合部的厚度对结合部的特性是有影响的[11-12]。设结合部虚拟材料的厚度为h,考虑两圆柱的半径与接触方式,可构建圆柱接触面积比

(14)

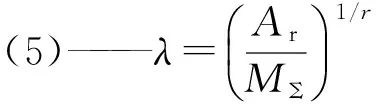
将式(9)和式(7)代入式(14)得

(15)

式中:λ0为圆柱初始接触面积比,并且有

(16)

将式(4)代入式(16)得

(17)

可见,式(17)不同于文献[10]中的式(10)

将内接触形式中的式(4)代入式(15)得

(18)

(19)

将右极限

(20)

代入式(19),可得内接触时

(21)

即当两圆柱大小相同、内接触时,两圆柱完全接触,式(13)退变成式(11),此时的情况与MB模型的建模条件相同。

3 两圆柱接触受力后的压缩总载荷

由式(14)易见

λ≤1

(22)

在总法向接触载荷P作用下,两粗糙表面为平面接触时,产生实际接触面积Ar。若将这2个粗糙表面弯曲成2个圆柱,当这2个圆柱为线接触时如果也产生相同的实际接触面积Ar,则此时两圆柱受径向压缩均匀分布总载荷F。通过平面接触构成平面低副,通过单一线接触形成线高副,故下面不等式成立

P≤F

(23)

分析式(22)与式(23),可令

P=λF

(24)

将式(15)代入式(24)得

(25)

MB模型可求解两粗糙表面为平面接触时的总法向接触载荷P,P的归一化形式即是两粗糙平面接触理论中的改进MB模型载荷公式[13-17]

(26)

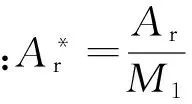
将式(26)代入式(25),可得F的归一化形式为

(27)

4 两圆柱接触受力后的赫兹应力

作用在-a≤x≤a长条上的法向压应力为

(28)

首先注意到法向压应力在整个接触区必须是非负的,即

(29)

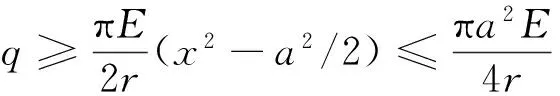
-a≤x≤a

(30)

为使不等式(30)恒成立,且两圆柱不被压溃而使连接失效,q或F(见式(1))不可能取值太大,再根据式(15),能保证不等式(22)成立,故可选较小值

(31)

式(31)与式(2)一致。由式(31)得

(32)

将式(32)代入式(28)得

(33)

函数p(x)在区间[-a,a]上的平均值(即平均法向压应力)为

(34)

将式(1)代入式(34)得

(35)

可见,两圆柱接触受力后,由于材料的弹性变形,接触区域是长为b、宽为2a的一个矩形。由式(33)可看出,接触表面上所承受的法向压应力是处处不相同的,其分布呈半椭圆柱形。初始接触线处的法向压应力最大,以此最大法向压应力代表两零件间接触受力后的应力,称为接触应力或赫兹应力,表示为

(36)

将式(36)除以式(34)得

(37)

将式(2)代入式(36)得

(38)

将式(1)代入式(38)得

(39)

5 两圆柱接触受力的数值模拟

2个圆柱的材料均为含碳质量分数0.45%的中碳调质45钢,弹性模量E1=E2=206GPa,泊松比ν1=ν2=0.3,最初屈服强度σy=550MPa,交货状态布氏硬度HB=700MPa,初始接触线长度b=50mm,大圆柱半径r2=100mm(文献[10]中大圆柱半径R1为1 000N有误,此外,取G=10×10-5也不合理)。

5.1 圆柱接触面积比的变化

图1给出了圆柱接触面积比的演化规律。图1a～1e都反映出2个共性规律:①圆柱接触面积比总是小于或等于1;②外接触时圆柱接触面积比小于内接触时的比率。

(a) h=1 mm与F=1 kN时小圆柱 (b) h=1 mm与r1=60 mm时总载荷 (c) h=1 mm与r1=r2时总载荷 半径对接触面积比的影响 对接触面积比的影响 对接触面积比的影响

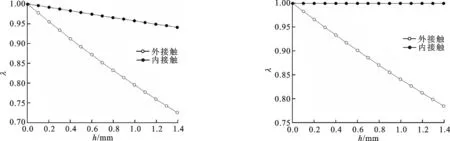
(d) F=1 kN与r1=60 mm时结合部虚拟 (e) F=1 kN与r1=r2时结合部虚拟 材料厚度对接触面积比的影响 材料厚度对接触面积比的影响

从图1a可见:λ随着r1的增加而增大;当r1→0时,λ→0,因为此时没有物体与从动大圆柱接触;当r1→r2且两圆柱为外接触时,λ<1;当r1→r2且两圆柱为内接触时,λ→1,因为此时两圆柱处处彻底内接触。

从图1b可见:λ随着F的增加而增大;当100N≤F≤1 000N时,在此大范围内λ收敛于某一定值,外接触时λ→0.770 9,内接触时λ→0.950 1;当0≤F≤100N时,在此小范围内λ很快从0增加到该定值。

图1c的演化规律与图1b类似,但内接触时的λ恒等于1,因为此时r1=r2,对于内接触是一种极限情况,两圆柱处处完全内接触,只要提供很小的外载荷F,λ就会立即从0增大到1。

从图1d可见,λ随着h的增加而线性衰减,当h=0时,λ=1。图1e的演化规律与图1d相似,但在内接触时λ恒等于1。

由图1b与1c可以看出, 当F=0时,

λ始终等

于0,因为对于任一正数x,0x=0,由式(15)可知F=0时λ=0,这不同于文献[10]中的结论“当F→0时,不论在外接触或内接触时,λ都达到最小值,但并不等于0,原因是尽管此时两接触体间的接触应力为0,但由于接触实体的存在,接触系数亦是存在的”。

5.2 实际接触面积的变化

图2给出了当h=1mm时实际接触面积的演化规律。图2a～2e皆能够说明以下3个共性规律:①本文的圆柱模型曲线位于MB模型曲线的下方;②在相同总载荷下,圆柱模型的实际接触面积比MB模型的小;③在产生相同实际接触面积的情况下,圆柱模型需要施加的总载荷比MB模型的大。

从图2a可见:不论是外接触还是内接触,同种接触方式的实际接触面积随着r1的增加而增加;外接触时的实际接触面积比内接触时的小。

从图2b可见:实际接触面积随着分形粗糙度的增加而减小;随着分形粗糙度的增加,产生特定实际接触面积所需要的总载荷增加,这是因为分形粗糙度增加时法向变形量增加,因此总载荷增加。

(a) D=1.5与G*=10-8时小圆柱 (b) D=1.5与r1=15 mm时分形 (c) G*=10-10与r1=15 mm时分形 半径对实际接触面积的影响 粗糙度对实际接触面积的影响 维数对实际接触面积的影响

(d) D=1.5、G*=10-10与r1=15 mm时 (e) D=1.5、G*=10-8与r1=15 mm时结合部 硬度对实际接触面积的影响 虚拟材料厚度对实际接触面积的影响

从图2c可见:对于给定的总载荷,当分形维数从1.4增加到1.5时,实际接触面积相应增加,而当分形维数从1.5增加到1.9时,实际接触面积转而减小。

硬度是定量表征材料软硬程度的一种物理参量,通常材料的硬度会随着距表面的深度而改变,不是一个恒定值。材料的布氏硬度HB对实际接触面积的影响如图2d所示,可见实际接触面积随着材料硬度的增加而减小。

结合部虚拟材料厚度对实际接触面积的影响如图2e所示,可见实际接触面积随着结合部虚拟材料厚度的增加而减小。

5.3 赫兹应力的变化

图3给出了当h=1mm、P=1kN时赫兹应力的演化规律:在同种接触方式下,本文方法计算的赫兹应力大于赫兹理论的计算值;随着r1的增加,赫兹应力下降;内接触时的赫兹应力小于外接触时的赫兹应力。

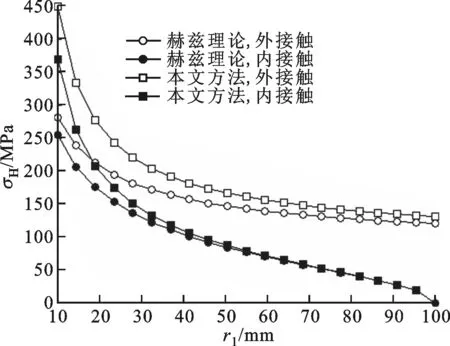
图3 小圆柱半径对赫兹应力的影响

6 结 论

(1)用术语“小圆柱面的面积”取代术语“公称接触面积”,更能直观表达圆柱的几何特征。

(2)圆柱接触面积比不大于1,外接触时的圆柱接触面积比小于内接触时的。圆柱接触面积比随着总载荷的增加或结合部虚拟材料厚度的减小而增大。

(3)外接触时的实际接触面积比内接触时的小。实际接触面积随着分形粗糙度、硬度、结合部虚拟材料厚度的增加而减小。对于给定总载荷,当分形维数从1.4增加到1.5时,实际接触面积相应增大;当分形维数从1.5增加到1.9时,实际接触面积转而减小。

(4)内接触时的赫兹应力小于外接触时的赫兹应力。

[1] HERTZ H. Über die berührung fester elastischer körper [J]. J Reine und Angewandte Mathematik, 1882, 92: 156-171.

[2] MAJUMDAR A, BHUSHAN B. Fractal model of elastic-plastic contact between rough surfaces [J]. ASME Journal of Tribology, 1991, 113(1): 1-11.

[3] MAJUMDAR A, BHUSHAN B. Role of fractal geometry in roughness characterization and contact mechanics of surfaces [J]. ASME Journal of Tribology, 1990, 112(2): 205-216.

[4] WANG Shao, KOMVOPOULOS K. A fractal theory of the interfacial temperature distribution in the slow sliding regime: part Ⅰ Elastic contact and heat transfer analysis [J]. ASME Journal of Tribology, 1994, 116(4): 812-823.

[5] WANG Shao, KOMVOPOULOS K. A fractal theory of the interfacial temperature distribution in the slow sliding regime: part Ⅱ Multiple domains, elastoplastic contacts and applications [J]. ASME Journal of Tribology, 1994, 116(4): 824-832.

[6] WANG Shao, KOMVOPOULOS K. A fractal theory of the temperature distribution at elastic contacts of fast sliding surfaces [J]. ASME Journal of Tribology, 1995, 117(2): 203-215.

[7] WANG Shao. Real contact area of fractal-regular surfaces and its implications in the law of friction [J]. ASME Journal of Tribology, 2004, 126(1): 1-8.

[8] HORNG J H. An elliptic elastic-plastic asperity microcontact model for rough surfaces [J]. ASME Journal of Tribology, 1998, 120(1): 82-88.

[9] JOHNSON K L. Contact mechanics [M]. 9th printing. Cambridge, United Kingdom: Cambridge University Press, 2004: 101.

[10]黄康, 赵韩, 陈奇. 两圆柱体表面接触承载能力的分形模型研究 [J]. 摩擦学学报, 2008, 28(6): 529-533. HUANG Kang, ZHAO Han, CHEN Qi. Research of fractal contact model on contact carrying capacity of two cylinders’ surface [J]. Tribology, 2008, 28(6): 529-533.

[11]田红亮, 刘芙蓉, 方子帆, 等. 引入各向同性虚拟材料的固定结合部模型 [J]. 振动工程学报, 2013, 26(4): 561-573. TIAN Hongliang, LIU Furong, FANG Zifan, et al. Immovable joint surface’s model using isotropic virtual material [J]. Journal of Vibration Engineering, 2013, 26(4): 561-573.

[12]TIAN Hongliang, LI Bin, LIU Hongqi, et al. A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools [J]. Elsevier International Journal of Machine Tools & Manufacture, 2011, 51(3): 239-249.

[13]张学良, 温淑花, 兰国生, 等. 平面结合面切向接触阻尼分形模型及其仿真 [J]. 西安交通大学学报, 2011, 45(5): 74-77, 136. ZHANG Xueliang, WEN Shuhua, LAN Guosheng, et al. Fractal model for tangential contact damping of plane joint interfaces with simulation [J]. Journal of Xi’an Jiaotong University, 2011, 45(5): 74-77, 136.

[14] 田红亮, 郑金华, 方子帆, 等. 阻尼系统的特征 [J]. 三峡大学学报: 自然科学版, 2015, 37(2): 75-82. TIAN Hongliang, ZHENG Jinhua, FANG Zifan, et al. Characters of damping system [J]. Journal of China Three Gorges University: Natural Sciences, 2015, 37(2): 75-82.

[15] 田红亮, 方子帆, 朱大林. 赫兹点接触133年 [J]. 三峡大学学报: 自然科学版, 2014, 36(2): 88-97. TIAN Hongliang, FANG Zifan, ZHU Dalin. 133 years of Hertz point contact [J]. Journal of China Three Gorges University: Natural Sciences, 2014, 36(2): 88-97.

[16] 左婧, 徐卫亚, 王环玲, 等. 岩石电镜扫描图像的分形特征研究 [J]. 三峡大学学报: 自然科学版, 2014, 36(2): 72-76. ZUO Jing, XU Weiya, WANG Huanling, et al. Fractal analysis of SEM image for rocks [J]. Journal

of China Three Gorges University: Natural Sciences, 2014, 36(2): 72-76.

[17] 田红亮, 赵美云, 郑金华, 等. 新的柔性结合部法向接触刚度和接触阻尼方程 [J]. 西安交通大学学报, 2015, 49(1): 118-126. TIAN Hongliang, ZHAO Meiyun, ZHENG Jinhua, et al. New equations of normal contact stiffness and damping for flexible joint interface [J]. Journal of Xi’an Jiaotong University, 2015, 49(1): 118-126.

[本刊相关文献链接]

蒲伟,王家序,杨荣松,等.重载下准双曲面齿轮传动界面润滑机理分析.2015,49(11):55-61.[doi:10.7652/xjtuxb2015 11010]

王东,徐超,万强.弹塑性接触粗糙表面切向载荷-位移模型.2015,49(11):122-127.[doi:10.7652/xjtuxb201511020]

刘伟强,张进华,洪军,等.椭圆抛物体形微凸体弹性接触力学模型.2015,49(10):34-40.[doi:10.7652/xjtuxb201510 006]

冯燕,俞小莉,刘震涛.应用热弹塑性理论的结合部法向载荷分形模型.2015,49(9):18-23.[doi:10.7652/xjtuxb201509 004]

褚坤明,王家序,蒲伟,等.混合润滑状态下滤波减速器的啮合冲击分析与修形方法.2015,49(7):140-148.[doi:10.7652 /xjtuxb201507023]

周安安,陈天宁,王小鹏,等.自仿射接触点及其在分形接触理论中的应用.2015,49(6):8-15.[doi:10.7652/xjtuxb2015 06002]

(编辑 葛赵青)

Contact Analysis of Cylindrical Pair with Parallel Axes

TIAN Hongliang,CHEN Tianmin,ZHENG Jinhua,YU Yuan,ZHANG Yi,ZHAO Chunhua

(College of Mechanical and Power Engineering, China Three Gorges University, Yichang, Hubei 443002, China)

A fractal contact model between two cylinders was set up through combining classic Hertzian theory and modern Majumdar-Bhushan model. The force acting on the linear higher pair rectangular contact plane of two cylinders was analyzed considering the virtual material thickness of joint interface and introducing the cylindrical contact area ratio. Numerical simulation shows that the cylindrical contact area ratio is not greater than one, and the ratio of outer contact is less than that of inner contact. This cylindrical contact area ratio can be increased by increasing the total load or reducing the virtual material thickness of joint interface. The real contact area in exterior contact is less than that in interior contact. As the fractal roughness, material hardness or virtual material thickness of joint interface increases, the real contact area decreases. When the fractal roughness is increased, the total load required to produce a particular real contact area also increases, which results from the fact that an increase in fractal roughness implies an increase in asperity deformation, hence a higher load is required. As the fractal dimension is increased from 1.4 to 1.5, the real contact area first increases under a given total load. However, if the value of fractal dimension is increased from 1.5 to 1.9, the real contact area decreases. The Hertzian stress in internal contact is less than that in external contact. These results may provide a basis for the fatigue strength computation of gear surface contact in cylindrical gear transmission.

machine design; joint interface; fractal contact; virtual material; cylinder; linear higher pair

2015-08-03。 作者简介:田红亮(1973—),男,博士,副教授;张屹(通信作者),男,教授。 基金项目:国家自然科学基金资助项目(51275273)。

时间:2015-11-03

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151103.1744.006.html

10.7652/xjtuxb201601002

TH113.1

A

0253-987X(2016)01-0008-08