计算脉冲电子束辐照下能量沉积剖面的新方案

刘 学 冉宪文,2 徐志宏 王 博 汤文辉（国防科学技术大学 理学院工程物理研究所 长沙 40073）

2（长沙理工大学 近地空间电磁环境监测与建模湖南省普通高校重点实验室 长沙 410073）

计算脉冲电子束辐照下能量沉积剖面的新方案

刘 学1冉宪文1,2徐志宏1王 博1汤文辉11（国防科学技术大学 理学院工程物理研究所 长沙 410073）

2（长沙理工大学 近地空间电磁环境监测与建模湖南省普通高校重点实验室 长沙 410073）

脉冲电子束辐照材料试验研究中，束流电子具有不同的速度和角度分布。但数值模拟计算一般都考虑电子束垂直入射靶材料，这可能导致数值计算结果与试验结果不符。针对该问题，提出了一种计算电子束辐照下能量沉积剖面的新方案，利用MCNP (Monte Carlo N Particle Transport Code)软件对铝、铜、钽金属材料在电子束辐照下的能量沉积进行模拟，分析了电子束垂直入射与带有角度分布入射时能量沉积的差异，为解释电子束辐照试验测量数据与理论计算结果之间的差异提供了依据。

脉冲电子束，电子束发散角，能量沉积剖面，仿真模拟

高空核爆条件下，爆炸能量的70%-85%以脉冲X射线形式释放。核爆产生的脉冲X射线能量很高，距离爆心10km处的能注量可达每平方厘米数百焦耳[1]。如此高能注量的X射线在亚微秒时间内辐照

到附近的航天器，可以导致航天器发生材料和结构破坏，致使航天器部分或完全毁坏。因此，研究脉冲X射线辐照下材料和结构的破坏机制具有重要意义。然而，迄今为止还没有如此高能注量、频谱相近的核爆X射线模拟源。所以，人们通常采用数值方法研究X射线与物质相互作用的热力学效应[2-3]，并采用低能强流脉冲电子束辐照试验来验证数值结果。

另一方面，在利用电子束试验验证材料在脉冲辐照下的热力学响应规律时，同样要采用数值方法研究电子束辐照下材料的热力学响应规律，以期获得较全面认识。然而在数值分析中，人们通常将电子束设定为垂直入射到靶材料表面，这与电子束试验装置中电子的实际运动不相符[4]。因此，造成了数值计算的初始条件与试验存在差别[3,5]，并可能造成数值计算结果与试验结果存在差异[6]，进而导致无法对相关试验数据做出合理的判断。

在数值分析中，要准确得到材料在电子束辐照下的热力学响应规律，关键因素包括能量沉积剖面、材料本构模型和参数等。基于上述现状，本文提出了一种计算电子束辐照下能量沉积剖面的新方案，期望能够更加逼真、准确地分析电子束试验现象。

1 计算方案

在电子束试验装置中，电子束从高功率二极管产生，然后经电磁场加速，最后入射至阳极靶。电子束加速原理如下：电子束从加速器阴极发出，经过加速电场后通过二极管阳极膜被注入到真空漂移管。在没有外加磁场时，电子束会受自身电磁场的作用[7]而产生径向发散，在极短的时间内（纳秒量级）就扩散到金属壁上，从而对束流的品质形成影响。为使电子束传输较远的距离则需要加入磁场，在磁场约束下电子束在传输路径上会产生束流包络振荡，即使最理想的加速器也很难实现平行、单能电子束的输出[5]。

实际上，电子并不是严格按照指定的方向飞散和加速，而是存在一定的发散角，如图1所示。胡杨[8]等采用MMLS (Modified Multi-layer Stacking)方法测量了在限定时刻下阳极靶面不同位置处的电子束入射角二维概率分布。结果表明：在电子束流箍缩不明显情况下，电子多以垂直或小角度（40°以下）轰击到阳极靶面。在电子束发射试验装置中，虽然可以测量电子束的能谱和发射电子的总能注量，但无法精确测量不同电子的飞散角度，从而也不能严格确定入射到靶材料表面的能注量。这就是实验条件的复杂性，所以实验数据往往具有较大不确定性。从有关文献数据可知[3,5,9-12]，在电子束辐照下，表面喷射冲量测量值一般总是大于理论计算值，而靶中热击波压力测量值却又小于理论值。

图1 电子束发散角模型Fig.1 Angle distribution model of electron beam.

1.1 模型建立与计算

电子束辐照热力学响应首先取决于电子束在靶材料内部的能量沉积剖面。因此，我们认为，理论计算结果与实验测量结果的差异可能与电子束在靶材料内部的能量沉积剖面在数值计算中没有被逼真地模拟出来有关。因为试验中电子束存在发射度，而数值分析中往往忽略了这一点[7]。为了对电子束辐照试验条件和相关数据进行深入分析，我们提出了一种计算电子束能量沉积剖面的新的数值分析方案：

1) 设定电子最大发散角。电子的发散角是指电子偏离其垂直入射靶材料表面方向的角度，电子垂直入射时发散角为0°。就某个电子而言，由于其加速过程的复杂性，可认为其飞散角是随机的（即以一定概率取某一角度）。但在确定的试验装置和确定的试验条件下，最大发散角是确定的。为此，可在数值计算中人为限定电子的最大发散角为β（从电子束与靶的相互作用效果看，电子的入射角等价于束流电子的发散角）。这样，电子将在以2β为圆锥顶角的圆锥体内随机飞行。数值模拟中，每一个有角度的电子，经随机抽样，将在0°至β角内随机分布。

2) 设定垂直入射电子的概率。文献[8]指出，在束流箍缩不明显时，大多数电子是垂直入射到靶材表面的。在模拟计算中，设这部分电子的概率为P1，其余电子则在0°到发散角β之间随机分布，其概率为P2，且P1+P2=1。

由于电子束最大发散角以及具有角度的电子的概率并不十分清楚，计算中可在一定范围内改变其数值，然后与相关试验结果进行对比。我们认为，通过大量计算与对比可能对试验装置中电子的飞散情况得到一定的认识。

1.2 能量沉积剖面计算结果与分析

理论表明，电子束的能量沉积过程与靶材料的原子序数Z有很大的关系。为了对不同原子序数的物质的电子束能量沉积形成认识，我们在计算中，选择了低Z、中Z和高Z的三种靶材料（铝、铜和钽）进行对比分析。

1.2.1 算例1

电子束垂直入射靶材料表面的概率设为P1=0.9，最大发散角依次设为5°、15°和25°三种情况，发散角内的电子束的发射概率为P2=0.1。图2给出了三种靶材能量沉积剖面的计算结果。

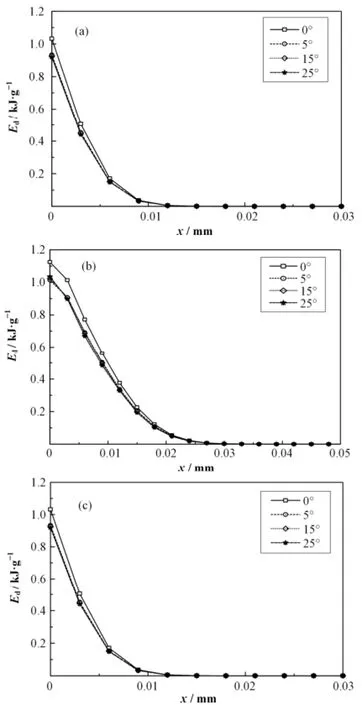
图2 不同发散角的电子束在不同金属靶材料中的能量沉积(a) 铝，(b) 铜，(c) 钽Fig.2 Energy deposition of different divergence angles of electron beam in different kinds of metals. (a) Aluminum, (b) Cuprum, (c) Tantalum

从图2可以看出，与垂直入射靶材料表面的电子束相比，当电子束存在发散角度时，其在铝、铜、钽三种靶材料内部的能量沉积峰值都将有所减小，峰值位置更靠近迎光面，但对穿透深度没有明显影响。例如，当电子束最大发散角取为5°时，在三种靶材料内部的能量沉积峰值相对于垂直入射时的能量沉积峰值降幅依次达到约9%、10%、11%。随着电子束发散角度依次增加，其在同一材料内部产生的能量沉积剖面相差不大，理论上能量沉积峰值会相应增加，峰值的位置也会逐渐靠近迎光面，穿透深度相应地减小。另外，随着靶材料原子序数的增加，电子束在靶材料内的穿透深度逐渐减小（如在铝、铜、钽内部穿透深度依次约为100μm、25μm、12.5μm），能量沉积曲线越来越陡峭，峰值位置更加靠近迎光面，这与不考虑电子束角度分布时所得到的计算结果基本相同。

从计算结果来看，电子束角度分布的存在对靶材料内部的能量沉积剖面存在一定影响。对于钽等高Z材料，不同角度分布的电子束辐照所得到的能量沉积剖面趋于一致。理论上，在同一垂直入射概率情况下，发散角越大，电子束在同一靶材料内部产生的能量沉积峰值也越大，其原因在于电子在靶材中的输运轨迹基本上为直线，能量确定的条件下其穿透深度也确定，入射角的存在并没有增加其穿透深度，反而降低了其垂直穿透深度。

对于取不同发散角时，电子束在同一种靶材料内部的能量沉积剖面相差不大这一现象可做如下解释：电子束垂直入射概率是确定的，电子在不同发散角内的方向分布是均匀分布，如图3所示。假设所取的发散角分别为θ1和θ2(θ1＜θ2)，电子束垂直入射的概率为P1。不同发散角的差别就在于对于发散角为θ2的电子束，电子在(θ1, θ2)方向内入射的概率为P =在算例1中，P1=0.9，当θ1=15°、θ2=25°时，P=0.04为一个很小的概率值。当电子数目不太多时，其在靶材料内部的能量沉积差别就变得十分微弱。

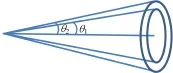
图3 不同发散角示意图Fig.3 Diagram of different divergence angles.

1.2.2 算例2

电子束最大发散角取为5°，垂直入射电子的概率依次取为0.9、0.8、0.7、0.6、0.5。三种靶材料中的能量沉积剖面如图4所示。

由图4可以看出，在电子束发散角相同的情况下，随着垂直入射概率的减小，电子束在三种靶材料内部的能量沉积曲线整体趋势相同。主要差异就

是能量沉积峰值随着电子束垂直入射的概率而依次减小，例如：垂直入射概率每减小0.1，电子束在铝靶内部产生的能量沉积峰值将减小约0.1kJ·g-1，但是峰值位置和穿透深度几乎没有差异，这在铜靶和钽靶内部仍具有类似的规律。这种现象可作如下解释：在有限尺度条件下，电子束垂直入射概率的减小意味着有更多的电子在侧向逃逸，而对能量沉积没有贡献，这与实际电子束打靶试验是相符的。

图4 5°发散角电子束在不同垂直入射概率下不同金属内的能量沉积(a) 铝，(b) 铜，(c) 钽Fig.4 Energy deposition of electron beam of 5° of divergence and different probabilities of perpendicular incidence in different kinds of metals. (a) Aluminum, (b) Cuprum, (c) Tantalum

2 结语

为了分析电子束辐照实验结果，本文提出了一种计算能量沉积剖面的新方案，即考虑电子束有一定的发散角。计算结果表明：

1) 在电子束能谱确定的条件下，存在角度分布的电子束比平行电子束在靶材料中所产生的能量沉积剖面峰值要低，且对原子序数越小的材料，其影响越明显。

2) 在电子束发散角一定的条件下，垂直入射电子的概率（或发散电子的概率）对能量沉积影响较大。

3) 对于具体的试验装置和试验条件，可以通过不断改变电子束发散角和垂直入射电子的概率进行计算，并与相应可比实验结果进行对比，从而对试验装置中电子束的飞散情况形成一定的认识。

在实际电子束打靶试验中，如果能够经过测量得到加速器所产生电子束的最大发散角，就可将此应用于数值模拟计算中，较垂直入射相比，能够有效减小与实验数据的差异，从而提升数值计算的准确性。

1 中国人民解放军总装备部军事训练教材编辑工作委员会. 核爆炸物理概论[M]. 北京: 国防工业出版社, 2003 Editorial Committee of the Chinese People’s Liberation Army General Armament Department of Military Training Materials. Introduction to nuclear explosion physics[M]. Beijing: National Defense Industry Press, 2003

2 周南, 乔登江. 脉冲辐照动力学[M]. 北京: 国防工业出版社, 2002 ZHOU Nan, QIAO Dengjiang. Dynamics of pulse irradiation[M]. Beijing: National Defense Industry Press, 2002

3 彭常贤, 林鹏, 唐玉志. 电子束在材料中的能量沉积和热激波特性[J]. 计算物理, 2003, 20(1): 52-58 PENG Changxian, LIN Peng, TANG Yuzhi, et al. Energy deposition and thermal shock waves of electron beam in materials[J]. Chinese Journal of Computational Physics, 2003, 20(1): 52-58

4 丁升, 周南. 电子束辐照冲量的数值计算与实验的对比[J]. 计算物理, 1997, 14(4-5): 646-648 DING Sheng, ZHOU Nan. Comparison of numerical calculation about impulse of electron beam irradiation and experiment[J]. Chinese Journal of Computational Physics, 1997, 14(4-5): 646-648

5 乔登江. 脉冲X射线热-力学效应及加固技术基础[M].北京: 国防工业出版社, 2012: 94 QIAO Dengjiang. X-ray thermo-mechanical response and basic technology of reinforce[M]. Beijing: National

Defense Industry Press, 2012: 94

6 周南, 丁升. 电子束辐照效应的数值模拟[J]. 计算物理, 1995, 12(3): 301-308 ZHOU Nan, DING Sheng. Numerical simulation of electron beam irradiation effect[J]. Chinese Journal of Computational Physics, 1995, 12(3): 301-308

7 章冠人. Tonks定律和电子束的发射度[J]. 强激光与粒子束, 1990, 2(2): 209-214 ZHANG Guanren. Law of Tonks and transmittance of electron beam[J]. High Power Laser and Particle Beams, 1990, 2(2): 209-214

8 胡杨, 杨海亮, 孙剑锋, 等. 强流电子束入射角二维分布测量方法[J]. 物理学报, 2015, 64(24): 52031-52037. DOI: 10.7498/aps.64.245203 HU Yang, YANG Hailiang, SUN Jianfeng, et al. A method of measuring the incidence angle of intense electron beam[J]. Acta Physica Sinica, 2015, 64(24): 52031-52037. DOI: 10.7498/aps.64.245203

9 王博, 冉宪文, 汤文辉, 等. 模拟X射线热-力学效应电子束能谱的优化研究[J]. 强激光与粒子束, 2014, 26(9): 094001. DOI: 10.11884/HPLPB201426.094001 WANG Bo, RAN Xianwen, TANG Wenhui, et al. Optimization of electron beam spectrum of simulating of X-ray thermo-mechanical response[J]. High Power Laser and Particle Beams, 2014, 26(9): 094001. DOI: 10.11884/HPLPB201426.094001

10 杨海量, 邱爱慈, 张嘉生, 等. 不同入射角度下强流脉冲电子束能量沉积剖面和束流传输系数模拟计算[J].强激光与粒子束, 2002, 14(5): 778-782 YANG Hailiang, QIU Aici, ZHANG Jiasheng, et al. Simulation calculation for the energy deposition profile and the transmission fraction of intense pulsed electron beam at various incident angles[J]. High Power Laser and Particle Beams, 2002, 14(5): 778-782

11 Stephen B S, James P H, Terry K, et al. The theory and simulation of relativistic electron beam transport in the ion-focused regime[J]. Physics of Fluids B: Plasma Physics, 1992, 4(5): 1332-1348. DOI: 10.1063/1.860088

12 汤文辉, 张若棋. 脉冲电子束对材料破坏效应的数值研究[J]. 强激光与粒子束, 1997, 9(4): 617-622 TANG Wenhui, ZHANG Ruoqi. Numerical research on the destructibility of pulsed electron beam to materials[J]. High Power Laser and Particle Beams, 1997, 9(4): 617-622

A new method for calculation of energy deposition profile of intense pulsed electron beam

LIU Xue1RAN Xianwen1,2XU Zhihong1WANG Bo1TANG Wenhui11(Institute of Engineering Physics, College of Science, National University of Defense Technology, Changsha 410073, China)
2(Institutes of Technology of Changsha, Monitoring and Modeling of Electromagnetic Environment in Near Space Key Laboratory of General Colleges and Universities of Hunan Province, Changsha 410073, China)

Background: In an electron beam experiment, electrons accelerated in electromagnetic field have different kinds of velocities and angles. However, in early numerical simulation calculations, the electron beam is always supposed to perpendicularly hit the surface of target materials, which will cause biases between simulations and experiments. Purpose: In this paper, a new method has been given to calculate energy deposition profile of intense pulsed electron beam which may explain the biases. Methods: MCNP (Monte Carlo N Particle Transport Code) is used to study metals such as aluminum, cuprum and tantalum. The differences between electron beam perpendicular to material and the one with angle distribution were worked out. Results: The results show that the energy deposition peak of pulsed electron beam with angular distribution is smaller than that of electron beam which is perpendicular. Conclusion: This may explain the biases between simulations and experiments.

Pulsed electron beam, Electron beam angle of divergence, Energy deposition profile, Simulation

LIU Xue, male, born in 1991, graduated from National University of Defense Technology in 2014, focusing on pulse radiation dynamics Corresponding author: TANG Wenhui, E-mail: 18175121477@163.com

TL7

10.11889/j.0253-3219.2016.hjs.39.120203

国家自然科学基金(No.11002162)、武器装备预研项目(No.51311020201)、长沙理工大学近地空间电磁环境监测与建模湖南省普通高校重点实验室

开放基金项目(No.20150104)资助

刘学，男，1991年出生，2014年毕业于国防科学技术大学，研究领域为脉冲辐照动力学

汤文辉，E-mail: 18175121477@163.com

Supported by National Natural Science Foundation of China (No.11002162), Weapon Equipment Development Project (No.51311020201), Project of Changsha University of Science and Technology, Near Space Electromagnetic Environment Monitoring and Modeling Key Laboratory of Hunan Province (No.20150104)

2016-06-17，

2016-10-27