无线传感器网络中的最大逼近突破路径算法

张红艳

（安徽建筑大学 电子与信息工程学院，安徽 合肥230601）

无线传感器网络中的最大逼近突破路径算法

张红艳

（安徽建筑大学 电子与信息工程学院，安徽 合肥230601）

在无线传感器网络中，感知覆盖的服务质量最重要的指标是感知覆盖区域和整个监测区域的比率。为此，提出一种解决覆盖问题的方法：首先引用覆盖问题(包括确定性覆盖和随机性覆盖)的概念，接着定义最大逼近突破路径的概念，然后利用Voronoi理论解决温度检测过程中的最大逼近突破路径问题，最后用实验仿真结果评估所提出算法的性能并讨论其在传感器网络覆盖领域的发展方向。

无线传感器网络；感知覆盖；最大逼近突破路径；Voronoi图

近些年，无线传感器网络技术被越来越多地使用，而且有望被应用在如健康、军事、家庭和环境监测等更多领域中。无线传感器网络由一些微小的传感器节点组成，每个节点都有感知环境的能力［1］，将这些节点部署在目标监测领域中，就可以组成一个无线传感器网络。

无线传感器网络中节点的部署、追踪以及覆盖问题是根本性问题，而感知覆盖和感知连通性则是两个基本问题［1-2］。其中，感知覆盖问题的研究已经应用到许多领域中，如在艺术画廊问题［3］中，要准确知道观看者的人数和位置，传感器就要覆盖整个画廊。

虽然许多研究者对无线传感器网络覆盖的问题都做过研究，但应用计算几何和Voronoi图来解决问题的却比较少。Meguerdichian等解决了特定传感器网络中针对服务质量的覆盖问题［4-5］：他们用多项式时间集中式算法来解决最坏覆盖的问题，而在解决最佳覆盖的问题时，研究空间定义成相对邻域图。该算法具有一些优势，如：（1）对最佳和最坏的情况分别采取了两种措施，得到了网络路径的关键规划结果，可指导网络节点的部署，提高网络的覆盖率；（2）适用于解决规划网络路径、观察物体以及其他许多方面的问题。但它也有如下缺点：（1）这是一种集中式的计算方法，故需要事先知道每个节点的位置信息；（2）算法不考虑实际的障碍、环境噪声等因素；（3）网络节点是同构的，不适用于实现具有不同覆盖能力节点的网络。因此，Meguerdichian等设传感器的感知能力随着距离的增加而减小，并据此提出了基于曝光的模型［6］。

在本文中，笔者描述了这样一个无线传感器网络：使用概率传感模型，由温度传感器检测室内温度，这里假设传感器的感知能力与距离成反比。

1　　相关理论

1.1模型和算法

（1）传感器网络概率感知模型。网络由分布在空间的自主式传感器节点组成，这些节点协同监测环境信息，如温度、声音、震动和压力等，每个节点都装有无线通信设备、微型控制器和电源（通常是电池）。网络成本取决于网络的规模和单个传感器节点的复杂程度，而这种成本约束会导致通信受到如能量、内存、运算速度和带宽等因素的限制。

概率感知模型［7］假设目标被检测到的概率和目标到传感器之间的距离呈指数关系，即Pij=e-ad（i,j），其中，d是目标与传感器之间距离，a表示传感器检测到目标的概率随距离减小的速度。

（2）传感器定位算法。本文使用欧式算法来确定节点位置，这种算法的优点是在特定条件下可以达到很高的精度，而且节点位置确定之后无需再修正。文中假设节点有接收信号强度（RSSI）测距能力，单个节点可以根据RSSI模型获得相邻节点与其自身之间的距离。

1.2计算几何Voronoi图和Delaunay三角

Voronoi图是由一组离散的点定义的基本构造。图1a为二维平面上一组离散点的Voronoi图，其中的离散点被划分为一系列凸多边形区域，每个多边形内的点都组成了相互间距离最近的一个网络。

Delaunay三角与Voronoi图直接相关，都是计算几何领域的典型问题。图1b显示的是一组随机放置的节点的Delaunay三角和对应的Voronoi图，其中虚线表示Delaunay三角，实线表示Voronoi图。

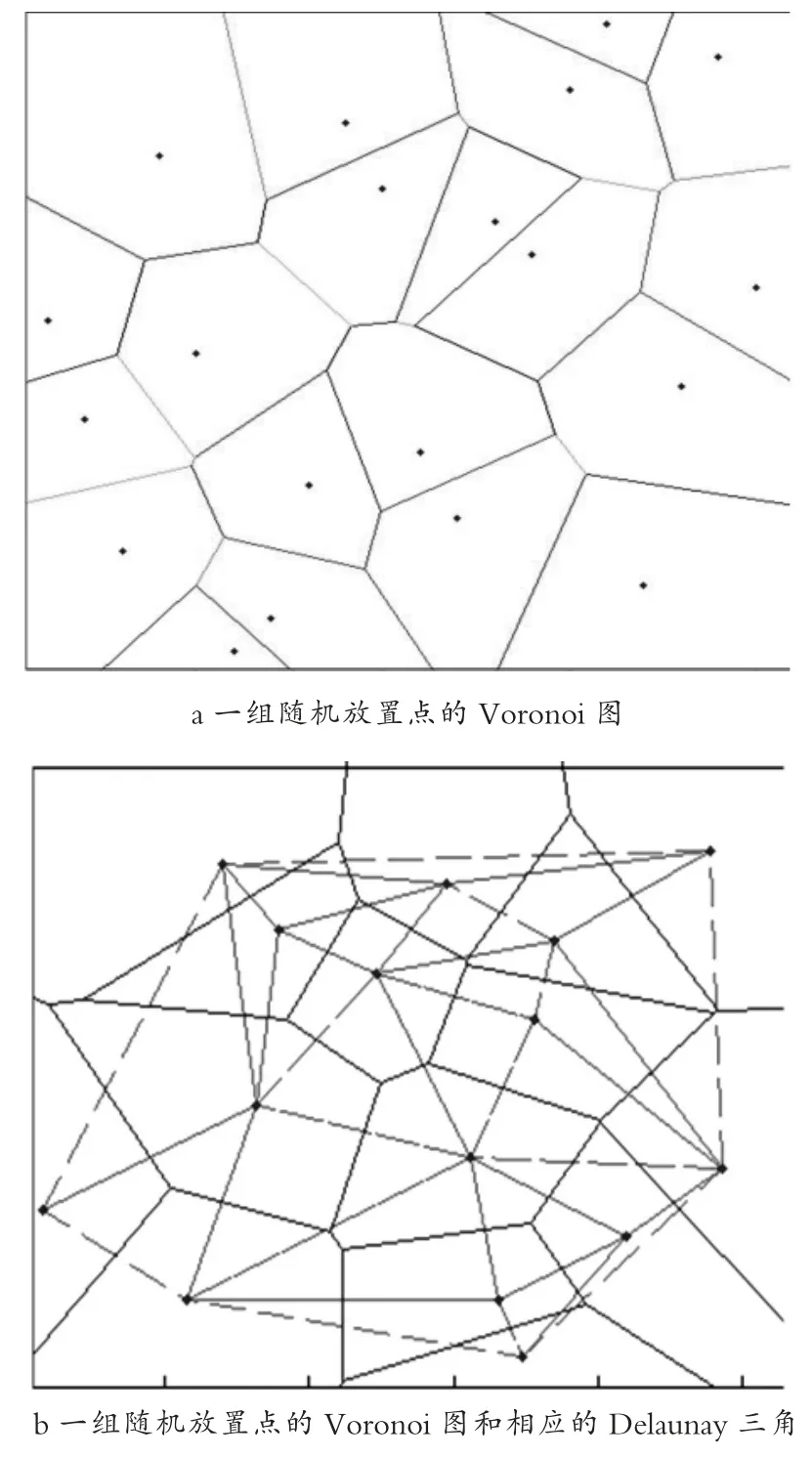
图1　　离散点的Voronoi图和Delaunay三角

1.3集中式与分布式实现方式

集中式计算是将所需信息发送到中央节点（如服务器）的一种计算方法，而分布式计算则依赖于节点之间的信息交换和节点位置坐标。

集中式计算的优点是全局规划，这使计算和存储能力方面不会受到过多限制，而且很容易得到相对准确的位置估计，不过，它会使靠近中心位置的节点由于通信开销过大而过早地消耗完电能，从而引起网络与中心节点之间的通信中断，无法实现实时定位。可见，分布式算法比集中式算法更具优势，特别是在降低通信成本方面，而设计无线网络的一个关键问题就是节约能源，因此，本文选择了分布式算法来实现无线传感器网络。

2　　最大逼近突破路径算法

2.1选择节点部署模型

根据传感器网络中节点分布的不同，可以将传感器网络的覆盖问题分为两大类：确定性覆盖和随机性覆盖。

确定性覆盖指的是传感器网络相对稳定或传感器网络是预设的特定形状，在节点位置已知的条件下完成覆盖目标区域或目标点的任务，关于3D艺术画廊的问题就是确定性覆盖问题的案例［3］。不过，在许多情况下，确定性部署都是不可行的，需要选择随机部署传感器的方法。

在目标监测应用中，移动目标沿任意路径通过部署区域时被检测到或不被检测到的概率属于栅栏覆盖问题。这种覆盖问题就是要最大限度地减小目标穿过检测区而未被发现的概率。

本文需要在某区域内使用温度传感器构成的网络中找到一个最大逼近突破路径，即穿过该区域而未被检测到的路径。在区域内随机部署传感器的同时还提出了一种分布式计算方法，即利用Voro n o i图和D elau n ay三角的特性去解决最大逼近突破路径的问题。

2.2问题描述

已知：在一个给定的目标区域A内，有一组传感器S，每个传感器节点Si的位置都可以通过位置算法得出，位置I和F是根据任务确定的，可以定义在传感区域的内部或外部。

问题：在区域A内找出始于I终于F的最大逼近突破路径PA。PA上任一点都具有从该点到与其最近传感器的距离是最大的属性。

2.3最大逼近突破路径算法

给Voronoi图的每一条边都赋予一个权重值，用来表示它与相邻节点间的最小距离。构建一个无向图T，其中的每个节点和每条边都对应Voronoi图中的一个顶点和一个线段。

最大路径查找算法如图2所示。在图2中，矩阵P用来存储最大路径的结果，矩阵D用来存储最大路径的权重。WUG是加权无向图，其中的元素是从某一节点到对应Voronoi图的边的垂直平分线之间的距离。在一次循环搜索过程中，设v和w均为Voronoi图中的顶点，I0为起点，V为终点。若P（v,w）=true，表明w是从I0到V中间所获得的顶点；如果Final（v）=true，那就是得到了从I0到V的最大路径。

在搜索过程结束后，可以找到一条从起点I到终点F的路径，这个路径就是最大逼近突破路径。图3是最大逼近突破算法，它调用了图2所描述的算法。

图2　　最大路径查找算法

图3　　最大逼近突破路径算法

3　　实验结果

实验采用Matlab来仿真算法，所有传感器节点的感知范围都使用相同半径的圆形区域来表示。为了使查找算法找到比较合理的最大逼近突破路径，假设起点I所在边的权值为0，终点F所在边的权值为所有权值中最大的值。

第一组实验对象是在2维欧几里得空间内给定的30个点，并且在相应的Voronoi图中不考虑权值。图4a所示为30个给定点的Voronoi图、Delaunay三角图以及最大逼近突破路径，其中粗线即为最大逼近突破路径。图4b为对应图4a中传感器节点的圆形感知区域。

第二组实验对象同样是在2维欧几里得空间内给定的30个点，但是在相应的Voronoi图中赋予权值。图5a所示为30个给定点的Voronoi图、Delaunay三角图以及最大逼近突破路径，其中粗线即为最大逼近突破路径。图5b为对应图5a中传感器节点的圆形感知区域。

通过对比图4b和图5b可以看出，第二组实验的结果要优于第一组实验。在已知传感器感知半径的前提下，图5b显示的从起点I到终点F的最大逼近突破路径基本是在传感器感知半径范围之外的，图4b显示的最大逼近突破路径有一部分是穿过传感器感知范围的，也就是说，选用第一组实验最大逼近突破路径穿过检测区被检测到的概率要比第二组大。

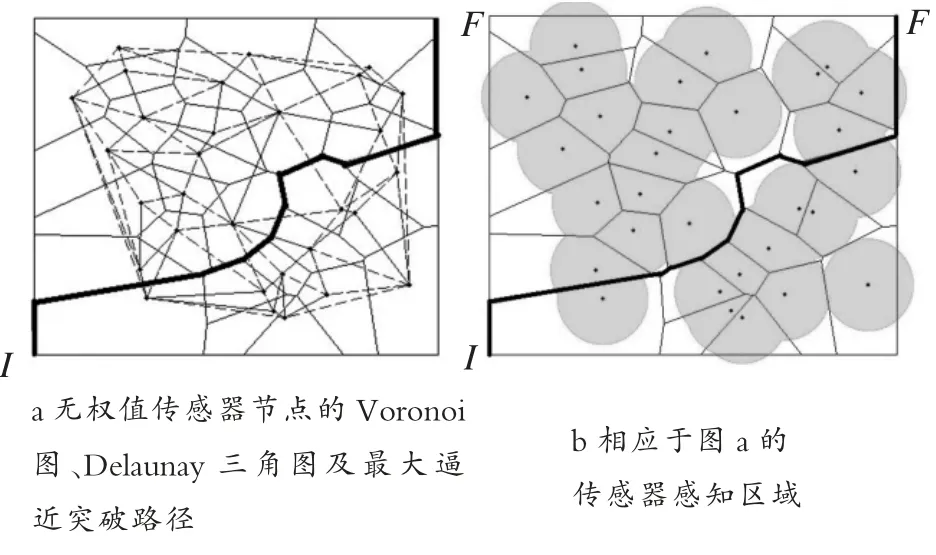
图4　　第一组实验结果

图5　　第二组实验结果

TP391

A

2095-7726（2016）12-0037-04

2016-07-10

安徽省教育厅自然科学项目（KJ2016A821），安徽建筑大学青年科研基金项目（2016XQZ12）

张红艳（1986-），女，安徽合肥人，硕士，研究方向：无线传感器网络技术及其应用。