重点医院对周边住宅价格影响的实证分析

张志峰

（哈尔滨商业大学 研究生学院，哈尔滨 250014）

重点医院对周边住宅价格影响的实证分析

张志峰

（哈尔滨商业大学 研究生学院，哈尔滨 250014）

文章以山东省立医院为例，利用特征价格模型，对重点医院与其周边住宅小区价格之间的关系进行了研究。结果表明：在不考虑方位影响的前提下，住宅小区距重点医院的距离与其价格之间并无显著的相关关系。而考虑方位影响，在研究距离范围以内东西方位和南北方位上，住宅小区到重点医院的加权距离与其价格均呈现显著的三次函数关系。在东西方位上，距重点医院0.83km以内，随距离的增加房价逐渐下降；在距重点医院0.83km-2.35km范围内，随距离增加住宅价格逐渐上升；南北方位上，在距重点医院1.03km以内，房价随距离增加而降低；在距重点医院1.03km-2.46km之间，房价随距离增加而增加。

三甲医院；房价；加权距离；济南

0 引言

医疗资源是一种公共服务设施，不仅能够满足居民日常看病的需求，而且对经济增长有很好的拉动作用[1]。随着社会的发展进步，人们物质生活水平提高，老龄化问题也越来越严重，生活水平提高也使得人们的健康意识不断提高[2]。然而医疗资源是有限的，分布也存在问题，看病难、看病贵仍然是人们较为关注的社会问题。这种日益增长的需求和有限的资源之间的矛盾依然没有得到有效解决，是源于医疗服务所具有的外部性、不确定性、即时性、信息不对称性。

济南作为山东省的省会城市，随着人口持续增长，医疗资源分配不均和优质资源稀缺的问题逐渐显现。那么，三甲医院作为稀缺资源对周边的住宅价格是否产生影响呢？遗憾的是目前仅有一些其他因素对房价影响的研究，例如轨道交通、大型绿地公园、政策因素、市场因素等[3-5]。在这个背景条件下，本文以山东省立医院为例研究了济南市重点医院对房价的影响，旨在为今后济南市房地产开发项目选址定位、产品策划以及营销策略的制定提供理论参考和实践指导。

1 医院选取与数据来源

1.1 医院的选取

济南市作为省会城市，医院以及周边住宅小区房价的相关数据资料众多，搜集、整理、分析存在较大难度，因此，本文将选择某一所代表性医院及其周边小区的数据来进行整理分析。山东省立医院是一所集医疗、教学、科研和预防保健、指导基层等任务于一体的省级综合性三级甲等医院，在济南市有非常高的认可度[6]。并且周边小区众多，数据采集方便，综合考虑各种因素，本次研究选择山东省立医院作为案例。

1.2 数据来源及样本描述

相关研究表明，学校、大型公园、轨道站点等大型公共服务设施对周边房价的辐射距离大概在2km左右[3-5]，本论文选取了山东省立医院周边直线距离2.5km以内的64个居民住宅小区作为样本点。为保证房价数据的可比性和准确性，研究样本均选取的是普通住宅（剔除了别墅、商业办公楼以及棚户区等），价格均采用小区平均价格，统一选取2015年5月到2016年4月份的房价交易数据计算样本小区交易均价。本文所涉及的距离存在一个假设条件：为了方便测量距离，此次研究将山东省立医院的中心位置假设成一个中心点，所有距离都是小区到此中心点的距离。为了提供数据的准确性，需得到三类距离：欧氏距离、街道距离、加权距离。欧氏距离是指小区到省立中心点的直线距离；由于人们主观感受的距离和实际到达途经的距离存在一定的差异，因此本文搜集了小区到医院中心点走主要街道所经过的距离，即街道距离；加权距离就是综合考虑这两方因素，取欧氏距离和街道距离的加权平均值(两方的权重分别为0.5和0.5)[7]。

具体数据的采集方式：①样本小区的价格（2015年5月-2016年4月）、房龄、容积率、绿化率、区域房价等信息是从安居客、房天下以及新浪乐居搜集而来并以必要的实地调查作为辅助；②小区到医院的距离（欧氏距离和街道距离）使用百度地图的测距工具采集并辅以必要的实地测量；③小区周边属性如有没有铁路、大型公园等是通过百度地图查看记录并辅以必要的实地调查。④小区的交通、医疗、教育、商业数据是通过安居客的登记数据采集得来。以上铁路是指500m范围内是否有铁路，大型公园指的是1000m范围内是否有大型公园。同时根据小区周边公园的数量及远近得出小区的公园分值。⑤学校等级是从搜学网上获取；网上评分是从认可度、评论等综合评价，本文是取小区对口中学和小学的评分加权值（二者的权重分别是0.5和0.5）。

2 研究模型及变量选取

2.1 研究模型的选取

多元线性回归模型是统计中比较简单直观的模型，但现实中房地产价格的变化情况是复杂的，可能不会单纯遵循线性关系。重复交易模型需要的样本数据是重复交易的，而这样的情况只占交易情况的极少部分，无法代表大多数的情况，数据也不好采集。因此，本次研究采用特征价格模型。由于特征价格模型中纳入了空间依赖和空间异质性，在本研究中将能够更好地发挥作用[8]。

2.2 变量的选取

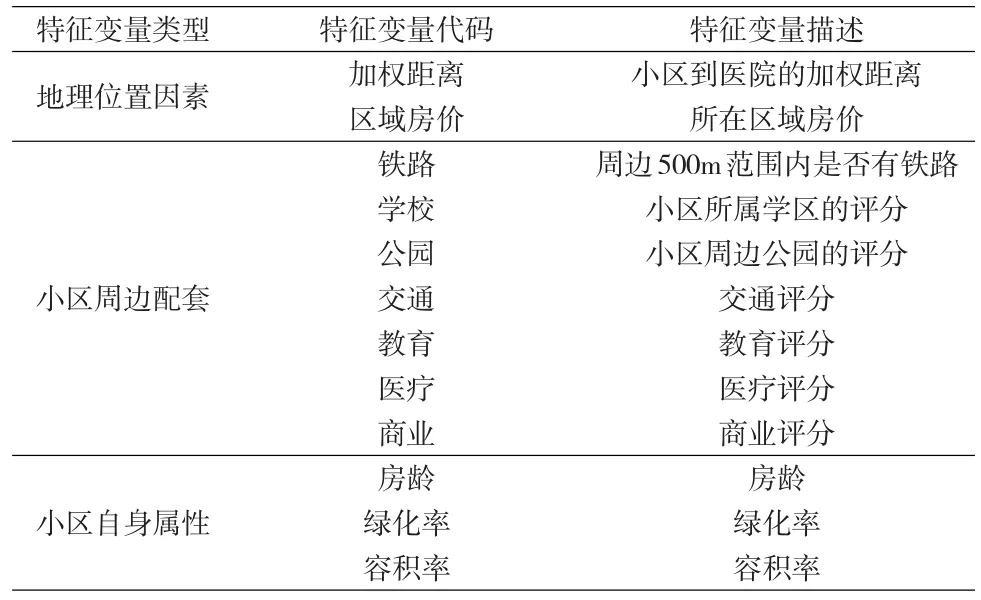
表1 特征变量列表

参考相关研究、文献资料以及济南目前的现实状况，本文将所搜集的数据资料分成三类特征变量：（1）地理位置因素，如样本小区到省立医院中心点的加权距离，样本所在板块的房价数据等；（2）小区周边配套，如附近是否有公园、附近是否有铁路等；（3）住宅自身因素，如小区的容积率、房龄、绿化率等。为了方便用SPSS软件进行分析，本文将小区周边配套设为虚拟变量，将0和1进行赋值。赋值情况为：小区周围500m内有高架的赋值为2，500-1000m的赋值为1，1000m以上的为0；公园分值是根据周边公园多少及距离从1到5进行划分；而医疗、商业、交通、教育的评分取自安居客上的评分，从1到5分为10个等级。特征变量的具体描述见表1，采集的数据信息描述见表2。

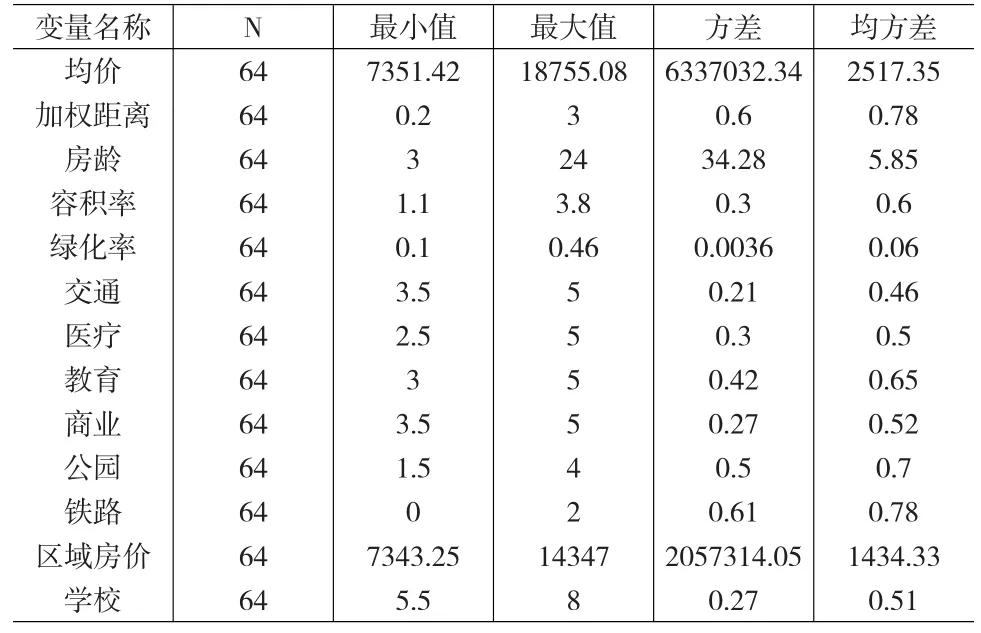
表2 数据信息描述

因为房地产价格具有非负特性，所以在一般研究里选取的基本模型多是半对数线性模型，它的形式一般是：lnp=α+β1X+β2X2+…+βiXi+…+βnXn[3]。

由于房地产价格和加权距离并不一定成一次线性关系，因此本文加入了三个特征变量（表3）来使模型的拟合更加准确完善。

表3 新增特征变量

3 重点医院对周边住宅小区房价空间影响力的总体分析与区域分析

3.1 空间影响力的总体分析

在使用SPSS软件进行分析时，要对搜集的数据信息做一定的处理，以便软件更好的采用我们的数据。首先，本文选取房地产平均价格的对数（lnp）作为此次回归分析的因变量，自变量是本文之前列出的加权距离、房龄、容积率、绿化率、交通、教育、医疗、商业、铁路、公园、学校、区域房价、加权倒数、加权平方、加权立方共15个特征变量。

对64个样本住宅小区的15个特征变量值进行线性回归分析，通过逐步回归的方式，发现有关距离的特征变量都被剔除（加权距离、加权倒数、加权平方及加权立方），最后剩余的区域房价、公园两个变量通过了显著性检验，此次分析中R2（模型拟合判定系数）=0.651，F（方差分析）= 27.9，Signif F（显著性检验值）=0.000＜0.05，拟合效果一般，分析中每个变量的回归系数如表4。

表4 逐步回归系数表

根据表中的各个数据可以得出，板块房价的Signif F＝0.000<0.05，系数是5.683，也就区域房价与房地产价格之间有显著的正向关系，即区域房价越高，房屋价值越高；公园等级的系数是2.274，Signif F＝0.026<0.05，即小区周边公园设施越完善，房屋价值越高。

虽然此次回归分析中与距离有关的变量都没有通过显著性检验，仅有两个变量通过了显著性检验，但这并不说明小区到医院的距离与房价之间没有关系。结合其他一些研究的过程，某些变量的显著性可能会受到某个显著性极高的变量的遮盖，而在整体看来这个显著性无法呈现出来，以致找不出相应关系。因此，本文尝试剔除区域房价的因素之后再进行逐步回归分析，观察小区到医院的距离是否会对房价产生影响。具体剔除方法：首先，选定10000为基准房价，将区域房价用合适的比率全部调整为10000；其次，根据此比率对小区均价进行相应调整。经过上述步骤的小区均价就变为剔除区域价格影响之后的均价。

将剔除区域房价因素之后的住宅价格对数作为因变量，除去区域房价之外的14个特征变量为自变量，第二次进行逐步线性回归分析，最后得到结果如表5。

表5 消除区域房价影响后的逐步回归系数表

由表5可见，只有公园这一个变量通过了显著性检验，其他14个变量都被一一筛选出去，结论与数据完善之前基本相同。即在未考虑小区方位因素的前提下，由全部样本数据来看，距医院的加权距离对周边住宅小区价格的影响并不显著。然而，这并不能排除不同方位的住宅小区价格与距医院的距离之间存在相关关系。出现上述结果，可能是不同方位的影响情况正向与负向影响共同作用的结果。因此下一步本文将采用小区方位这个虚拟变量来进行深度分析，即将所有的住宅小区分为东西和南北两类方位进行分析。

3.2 空间影响力的区域分析

把常用的四象限坐标系顺时针转动45度，那么整个坐标图划分为四个范围，方位设置如图所示上下两个区间是南北方位，左右两个区间是东西方位。把所有的样本小区根据方位进行分组，落于南北方位的共37个住宅小区，落于东西方位的共27个住宅小区。

3.2.1 东西方向的空间影响力区域分析

首先对东西方位的27个住宅小区的样本进行分析，在前述研究的前提下，本次分析的因变量依旧选择剔除区域房价因素之后的房价对数，自变量是住宅小区到省立医院的加权距离。使用SPSS 22软件进行曲线估计，选择线性、二次项、复合、增长、对数、立方、S型、指数分布、逆模型、幂函数以及logistic模型，最后的输出结果显示立方函数的拟合情况是最贴近的。模型总结见表6。

表6 东西方位模型总计和参数评估

由上表可以得出三次函数的拟合效果是最好的，R2（拟合判定系数）=0.453，F（方差分析）=6.357，Signif F(显著性概率)=0.003<0.05，证明在东西方位上，住宅小区到省立医院的加权距离和小区房屋均价之间有显著的三次函数关系，最终的曲线拟合函数：

（1）式中，p为剔除区域房价后的小区均价，X为小区至省立医院的加权距离。对（1）式求导后得到两个极值点，分别为0.83和2.35。即在东西方位上，在0.83km以内，随着小区到医院距离的增加，房价是逐渐下降的，从样本数据看是下降了3815元；在0.83km-2.35km范围内随着距离增加小区房价逐渐上升，上升的幅度是9000元。这是因为许多中老年或子女同父母同住的家庭更愿意选择省立医院近的小区，以便于就医方便。另一方面对于医疗需求不是那么急切的家庭可能会因病菌考虑一个安全距离，既不会离医院太近，但到医院交通时间又不会太长。这也就导致在之后房价又会出现一个最高点。同时在本次研究范围的边界处正东方是老城区位置，正西方有市立五院和儿童医院，这也可能是导致两端房价上升的原因，即两种公众设施辐射圈的交汇处。

3.2.2 南北方向的空间影响力区域分析

在南北方位上，采用和东西方位同样的研究方法，此次的因变量还是选择剔除区域房价因素之后的房价对数，自变量是住宅小区到省立医院的加权距离。选择线性、二次项、复合、增长、对数、立方、S型、指数分布、逆模型、幂函数以及logistic模型对37个样本数据进行曲线拟合。最后的输出结果显示立方函数的拟合情况是最贴近的。模型总结见表7。

表7 南北方位模型总计和参数评估

由上表可知，南北方位拟合效果最好的仍然是立方函数，R2(拟合判定系数)=0.311，F（方差分析）=4.968，Signif F（显著性概率）=0.006<0.05，说明在南北方位上，房价与小区到医院的距离之间呈显著的三次函数关系，其拟合函数关系式为：

（2）式中，p为剔除区域房价后的均价，X为小区至医院的加权距离。对上述函数求二阶倒数，得到两个极点，1.03和2.46。即在1.03km以内，房价随距离增加而降低，在此1km内房价是下降了2543元；在1.03km-2.46km之间房价随距离增加而增加，此范围内总共增加了4009元。这个情况与东西方向的结论类似，只是距离节点因为某些影响因素的存在而导致有些差异。原因同样也是一类家庭希望就在医院近距离范围内，以便就医，另一类家庭则是选择与医院保持一定的距离，即交通便利，又减少了医院的负面影响。同样在研究范围边缘处的火车站以及英雄山风景区也是导致房价在第二段逐渐升高的一个因素。

4 结论

本文以山东省立医院为例，研究了重点医院对周边住宅小区房价的影响，结论表明：

（1）东西方位上，房价与小区到医院的距离之间呈显著的三次函数关系，即在0.83km以内，随着小区到医院距离的增加，房价逐渐下降；在0.83km-2.35km范围内随着距离增加小区房价逐渐上升。究其原因，主要有以下几方面：一是因为许多中老年或子女与父母同住的家庭更愿意选择省立医院近的小区，以便于就医方便。二是因为其余家庭可能会因医院周边的病菌考虑一个安全距离，不会离医院太近，但到医院交通时间又不会太长。三是在我们研究范围的边界处正东方是老城区位置，正西方有市立五院和儿童医院，这也可能是导致两端房价上升的原因，即两种公众设施辐射圈的交汇处。

（2）南北方向上，二者同样呈显著的三次函数关系，在1.03km以内，房价随距离增加而降低，在1.03km-2.46km之间房价随距离增加而增加。除了与东西方向的前两个原因外，在研究范围边缘处的火车站带来的便利交通以及英雄山风景区带来的居住环境也是导致房价升高的一个因素。

上述研究结论表明，重点医院对周边住宅小区房地产价格存在一定影响，并且在不同区区域范围内的作用效果也不尽相同。随着居民生活水平的提高，住宅需求也会提升，就医的便利性、及时性都会在房价中有所体现，同时也将成为客户选择房产产品的关注点。本文的研究结论可以为房地产开发产品定位和营销策划提供参考。房地产开发企业可以根据离医院的距离确定恰当的产品定位和营销策划方案。

[1]斯子文.三甲医院对人口分布及房价影响的研究——以复旦大学附属儿科医院为例[J].经济地理，2013，(10).

[2]彭希哲，胡湛.公共政策视角下的中国人口老龄化[J].中国社会科学，2011，(3).

[3]胡国桥.轨道交通对房地产价值的影响研究[D].重庆：重庆大学，2008.

[4]金杰，张洪.地价和房价空间变化研究--以昆明市为例[M].昆明：云南科技出版社，2012.

[5]周兰兰.西安浐灞湿地公园对其周边住宅价格影响的研究[D].西安：西安理工大学，2015.

[6]王省.省立医院（集团）东营医院挂牌成立[J].山东卫生，2011，(7).

[7]吴新生.基于空间内涵资产定价模型的商品住宅价格溢价测度研究[J].价格月刊，2013，(2).

[8]孙久文.空间计量经济学均研究范式与最新进展[J].经济学家，2014，(7).

（责任编辑/易永生）

C915

A

1002-6487（2016）21-0106-03

张志峰（1976—），男，辽宁锦州人，副教授，研究方向：产业升级。