可信度诱导犹豫模糊优先级平均算子及其应用

韩莉娜，刘小勇

(华南理工大学 经济与贸易学院，广州 510006）

可信度诱导犹豫模糊优先级平均算子及其应用

韩莉娜，刘小勇

(华南理工大学 经济与贸易学院，广州 510006）

文章研究了考虑可信度和对属性有偏好的犹豫模糊信息集成问题。对每一个犹豫模糊数给出相应的可信度，用来表示专家对属性的熟悉程度。考虑到可信度的重要性，在优先级平均算子（PA）基础上提出了可信度诱导犹豫模糊优先级加权平均(CHFPWA)算子，并给出了该类算子的优良特性。最后，利用数值案例验证了所提方法的有效性和优越性。

犹豫模糊集；信息集成；优先级；可信度

0 引言

犹豫模糊集（HFS）是Torra[1]在模糊集（FS）基础上扩展而来的一类广义模糊集，HFS最大特点是允许一个属性同时出现不同的评价值，目前HFS已经被进一步应用到诸多领域。运用犹豫模糊集进行决策的一个关键技术是犹豫模糊信息集成，特别是加入偏好信息的加权算子集成。现有的算子在集结时，往往忽视了决策者的知识背景。为了考虑决策者对专业领域的熟悉程度（即可信度），Xia和Xu[2]提出一种可信度诱导犹豫模糊集结算子，并将其运用到供应商选择中。阮传扬[3，4]等提出了几类可信度诱导犹豫模糊加权集成算子并讨论了其优良性质，然后将其与熵值修正G1组合赋权法结合，提出了一种多属性决策方法。刘小弟[5]等研究了对方案有偏好且考虑可信度的犹豫模糊多属性决策方法，并用数值案例验证了其有效性。

不难发现，以上方法侧重点均各不相同，而在犹豫模糊集中考虑可信度的影响，结合属性的优先级进行信息集成的方法截止目前还未见有所研究。基于此，本文将从犹豫模糊信息出发，研究一种新的加权集成算子：可信度诱导犹豫模糊优先级加权平均（CHFPWA）算子，并给出了新算子存在的特性以及运算规则。最后，本文构建了一类考虑可信度和属性优先级的犹豫模糊多属性决策方法。

1 犹豫模糊集基本理论

Zadeh[6]首次尝试用隶属函数这一数学方法来表达不确定的信息，然而在很多实际决策问题中存在着大量的不确定性，为了解决某一评价指标同时出现不同评价值的现象，Torra[1]提出了犹豫模糊集的概念。

定义1[7]：若存在一个非空集合X={x1，x2…xn}，则犹豫模糊集即为从X={x1，x2…xn}到[0，1]的一个子集的函数，为了易于理解，可以用如下数学公式表示：

其中hE(x)表示隶属于[0，1]中的几个可能隶属值的集，xÎX表示在集合E中的隶属度的集合。

定义2[7]：若存在一个非空犹豫模糊集合h，则称：

为h的得分函数，其中#h为犹豫模糊集h中的元素的个数。

假设存在两个犹豫模糊集h1和h2：

（1）若s(h1)s(h2)，则h1h2;

（2）若s(h1)=s(h2)，则h1=h2。

根据犹豫模糊集的特性及其直觉模糊集的运算规则，Xia[2]给出了基于犹豫模糊集h，h1和h2的一些基本运算规则：

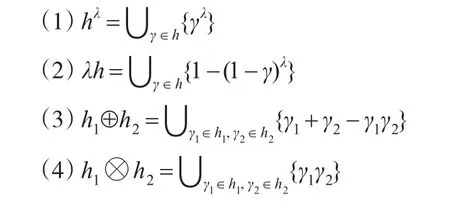
考虑到属性优先级的影响，Wei[2]在优先级平均(PA)[9]算子的基础上提出了犹豫模糊优先级加权平均(HFPWA)算子，定义如下：

定义3[8]：设一组犹豫模糊数hj(j=1，2…n)，则犹豫模糊优先级加权平均集成（HFPWA）因子定义如下：

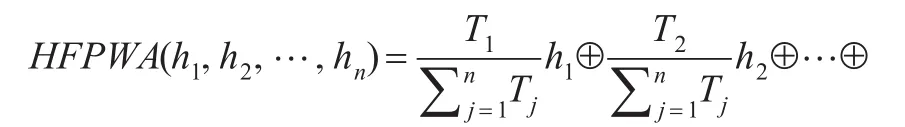
定义4[2]：设存在犹豫模糊集h1，h2…hn，"γiÎhi，liÎ[0，1]表示与γi相对应的可信度（即专家对该领域的熟悉程度），且hi(1=1，2…n)的权重向量为，则：

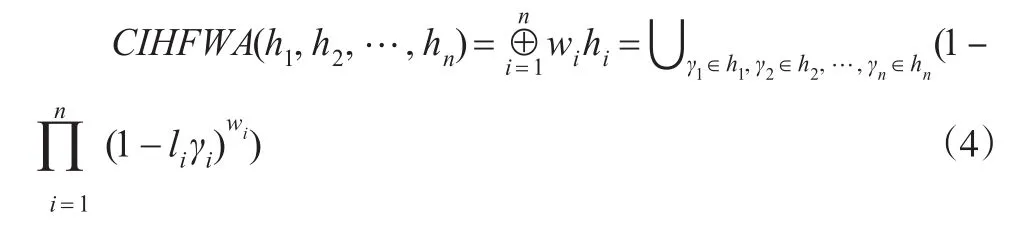
称为可信度诱导犹豫模糊加权平均(CIHFWA)算子。

2 考虑可信度和属性优先级的犹豫模糊加权平均算子

基于现有的犹豫模糊信息集成算子，考虑到可信度的重要性，本文提出可信度诱导犹豫模糊优先级加权平均（CHFPWA）算子。

定义5：设一组犹豫模糊数hj(j=1，2…n)，"γjÎhj，ljÎ[0，1]表示与γj相对应的可信度，且设CHFPWA:Ωn®Ω，若：

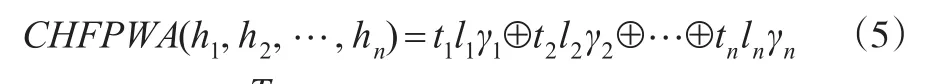
根据犹豫模糊集的运算规则，可以得到如下的定理：

定理 1：设一组犹豫模糊数 hj(j=1，2…n)，"γjÎhj，ljÎ[0，1]表示与γj相对应的可信度，则通过CHFPWA算子集结后仍然为犹豫模糊数，且：

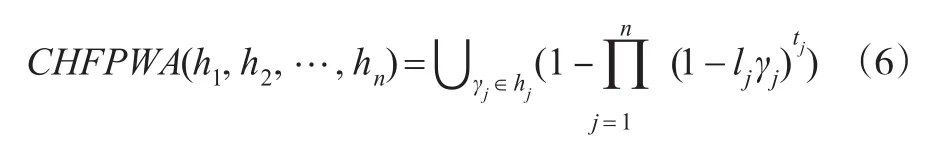
证明：本定理可以采用数学归纳法证明：

可得：

则即当n=2时，原式成立。

当n=k+1时，

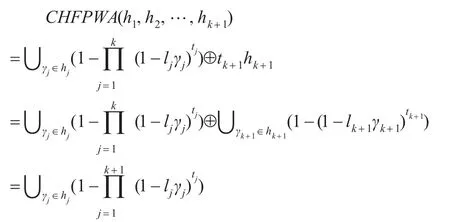
即当n=k+1时，原式仍成立，则即原式对任意的n都成立。

可以很容易的证明CHFPWA算子还具有下列性质：

定理2：若所有犹豫模糊数满足h1=h2=…=hn=h*，则有：

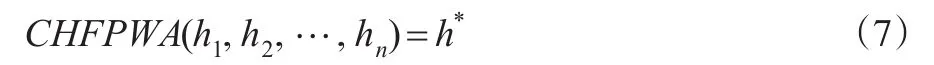
定理3：设一组犹豫模糊数 hj(j=1，2…n)，若，则：

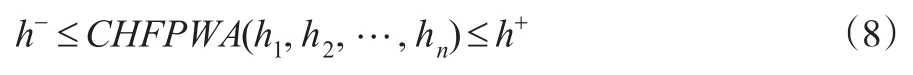
定理4：设一组犹豫模糊数hj(j=1，2…n)，若r>0，f为一犹豫模糊数，则：

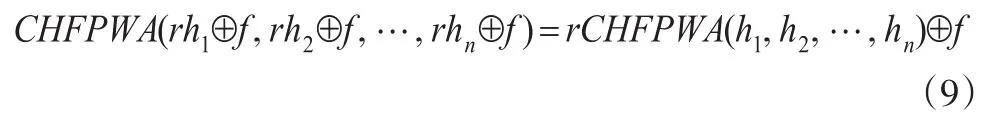
定理 5：设两组犹豫模糊数 hj(j=1，2…n)，fj(j=1，2…n)，则：

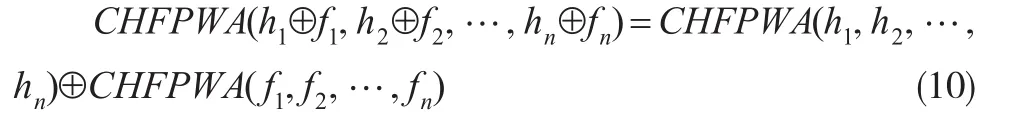
3 基于CHFPWA算子的多属性决策方法

基于CHFPWA集成算子，本文给出一种考虑可信度并且具有属性偏好信息的犹豫模糊多属性决策方法。设A={A1，A2…Am}为方案集，G={G1，G2…Gn}为属性集且存在优先级序关系，如G1G2…Gn，表明属性集的优先级关系依次递减。专家组E={e1，e2…ep}对方案AiÎA关于属性GjÎG进行匿名评估。由于专家来自不同领域并且具有不同的专业背景，为了得到更合理的结果，每位专家给出每个方案AiÎA关于每个属性GjÎG的评估值之后，同时根据其对属性的熟悉程度给出与属性值相对应的可信度，删除掉完全重复的数据，就组成了一个犹豫模糊决策矩阵，本文用H=(hij)m´n来表示。假设tij(i=1，2…m;j=1，2…n)表示第i个方案第j个属性的优先级混合权重。详细步骤如下:

步骤1:首先利用定义5计算带有可信度和属性偏好信息的权重tij(i=1，2…m;j=1，2…n)。

步骤2：利用 CHFPHA算子集成犹豫模糊矩阵H=(hij)m´n，得出候选方案 Ai的综合表现值

hi(i=1，2…m)。

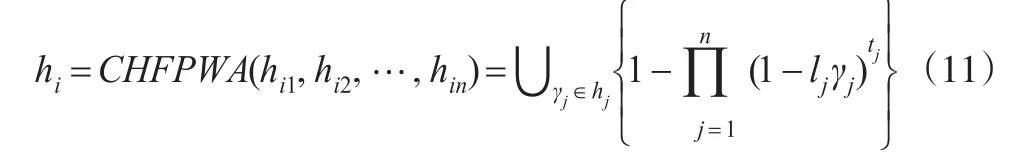
步骤3：根据式（2）中的犹豫模糊得分函数公式计算hi(i=1，2…m)的综合得分

则得分函数s(hi)越大，所对应的候选方案Ai越优。

4 数值算例

假设某突发事件有五个应急预案Aj(j=1，2，3，4，5)，决策小组拟从以下四个方面对其进行评价：G1：处置的快速性，G2：内容和费用的合理性，G3：保障的充分性，G4：广泛适用性。若评审专家组给出的属性重要程度如下：G1G2G3G4。为了得到更加合理的结果，领导小组聘请了由高校的应急管理学者、政府机关的应急管理领域专家以及相关公司的应急管理专家组成的4人评审专家小组。4位专家 E={e1，e2，e3，e4}分别对五个应急方案Ai(i=1，2，3，4，5)下的各个属性 Gj(j=1，2，3，4)进行匿名评估。由于专家来自不同领域并且具有不同的专业背景，为了得到更合理的结果，每位专家给出每个方案AiÎA关于每个属性GjÎG的评估值之后，同时根据其对属性的熟悉程度给出与属性值相对应的可信度，删除掉完全重复的数据，这样就组成了一个犹豫模糊决策矩阵H=(hij)m´n，具体决策矩阵见表1所示。

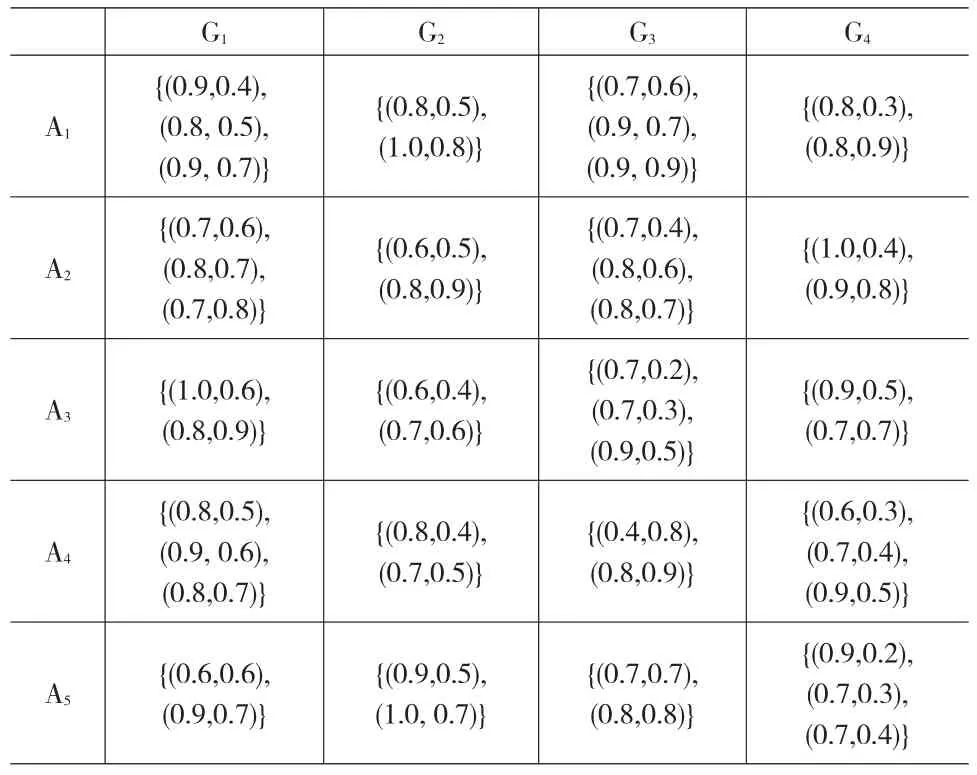
表1 犹豫模糊决策矩阵

为了得到最优的应急预案，本文首先构建了一种利用CHFPWA算子来处理犹豫模糊评价信息的多属性决策方法，详细步骤如下：

步骤1:利用定义5计算带有可信度和属性偏好信息的权重tij(i=1，2…m;j=1，2…n)的值。

步骤2：利用CHFPHA算子集成犹豫模糊矩阵H=(hij)m´n的第i行，得出候选方案 Ai的综合表现值hi(i=1，2…5)，由于hi中的数据过多，因此就不一一列取，仅以候选方案A1的综合表现值h1为例，其他类似。

h1={0.3692，0.4091，0.4636，0.3901，0.4287，0.4814，0.5262，0.5562，0.5972，0.5165，0.5471，0.5889，0.5325，0.5621，0.6025，0.6369，0.6598，0.6912，0.4235，0.4599，0.5098，0.4426，0.4778，0.5260，0.5670，0.5944，0.6318，0.5581，0.5860，0.6242，0.5728，0.5998，0.6367，0.6681，0.6891，0.7178}

步骤3：根据式（2）中犹豫模糊得分函数公式计算hi(i=1，2…m)的得分如下：

则s(h1)s(h3)s(h2)s(h5)s(h4)

得分函数s(hi)越大，所对应的候选方案Ai越优，因此最优候选应急预案为A1。

为了选择最佳应急预案，若不考虑可信度而选择文献[2]中的犹豫模糊优先级加权平均（HFPWA）算子进行集成的话，具体决策步骤如下[2]：

步骤1':利用定义3中的式（3）计算Tij(i=1，2…m; j=1，2…n)的值如下：

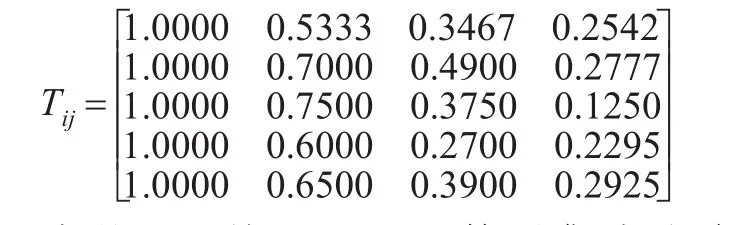
步骤2'：利用HFPWA算子集成犹豫模糊矩阵H=(hij)m´n的第i行，得出候选方案 Ai的综合表现值hi(i=1，2…5)，由于hi中的数据过多，因此就不一一列取，仅以候选方案A1的综合表现值h1为例，其他类似。

步骤3'：根据定义2中犹豫模糊得分函数公式计算hi(i=1，2…m)的得分如下:

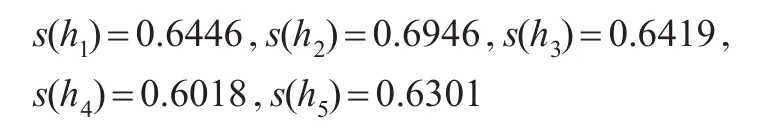
则s(h2)s(h1)s(h3)s(h5)s(h4)

得分函数s(hi)越大，所对应的候选方案Ai越优，因此最佳候选应急预案为A2。

5 结论

本文研究了考虑可信度以及属性优先级的犹豫模糊信息集成算子。由于决策者来自不同的部门，具有不同的专业知识背景，必然会导致对某些知识领域熟悉程度的不同。因此，在对候选方案中的属性进行评价时，应该有相应的可信度用来表示专家对该领域的熟悉程度，这样得到的结果才更加合理、可信。为了对不同专家提供的具有可信度的犹豫模糊信息进行区别和集成，本文提出了可信度诱导犹豫模糊优先级加权集成（CHFPWA）算子，该类算子既能保证属性优先级恒定，又可以考虑专家对该领域的熟悉程度。与文献[2]相比，本文所提方法具有良好的区分度，计算操作相对简单、科学，从而可以有效地对方案进行抉择。

[1]Torra V.Hesitant Fuzzy Sets[J].International Journal of Intelligent Systems，2010，25(6).

[2]Xia M M，Xu Z S，Chen N.Induced Aggregation Under Confidence Levels[J].International Journal of Uncertainty，Fuzziness and Knowl⁃ edge-Based Systems，2011，19(2).

[3]阮传扬，杨建辉.考虑可信度和属性优先级地犹豫模糊决策方法[J].运筹与管理，2016，25（3）.

[4]Ruan C Y，Yang J H.Hesitant Fuzzy Multi-attribute Decision-making Method Considering the Credibility[J].Journal of Computational Infor⁃mation Systems，2015，11(2).

[5]刘小弟，朱建军，张世涛.考虑可信度和方案偏好地犹豫模糊决策方法[J].系统工程与电子技术，2014，25（3）.

[6]Zadeh L A.Fuzzy Sets[J].Information and Control，1965，8(3).

[7]Xia M M，Xu Z S.Hesitant Fuzzy Information Aggregation in Decision Making[J].International Journal of Approximate Reasoning，2011，(52). [8]Wei G W.Hesitant Fuzzy Prioritized Operators and Their Application to Multiple Attribute Decision Making[J].Knowledge-Based Systems. 2012，(31).

[9]Yager R R.Prioritized Aggregation Operators[J].International Journal of Approximate Reasoning，2008，(48).

(责任编辑/易永生)

O21

A

1002-6487（2016）21-0069-03

国家自然科学基金资助项目（71173076）；广州市哲学社科规划课题（15Q04）

韩莉娜（1990—），女，河南濮阳人，硕士研究生，研究方向：区域经济学。

（通讯作者）刘小勇（1980—），男，江西吉安人，博士，副教授，研究方向：财政税收、区域经济发展。