区间DEA供应链合作伙伴评价模型

向小东，张哲远

（福州大学 经济与管理学院，福州 350116）

区间DEA供应链合作伙伴评价模型

向小东，张哲远

（福州大学 经济与管理学院，福州 350116）

供应链合作伙伴评价是供应链管理领域中重要问题之一。文章在确定条件下带有双重角色变量CCR模型基础上，构建了带有双重角色变量的区间CCR供应链合作伙伴评价模型，给出了模型的求解步骤。最后，举例说明了模型的应用。

供应链合作伙伴评价；双重角色变量；区间效率；数据包络分析

0 引言

供应链合作伙伴评价问题一直以来都是国内外学者研究的重点、热点和难点之一，多种不同的方法被应用到了供应链合作伙伴评价问题中，其中DEA方法是主要被应用的方法之一。在以往应用DEA方法进行供应链合作伙伴评价的研究中，国内外学者做了许多卓有成效的工作。Cook等指出并不是所有因素都可以清楚的被归为输入或输出，有些特别的因素同时起到输入和输出的作用，这些因素被称为双重角色变量，在运用DEA方法时将双重角色变量因素考虑入模型是有必要的，它会对评价的结果产生影响[1]。近年来，将双重角色变量纳入到DEA方法中进行供应链合作伙伴的评价已经成为新的研究趋势[2-4]。

另一方面，在现实中，由于经济因素、环境因素等原因，被考察的候选合作伙伴的观测数据可能存在不确定性，观测值可能呈区间数的形式，此时确定的DEA模型不再适用，需要运用区间DEA方法对供应链合作伙伴进行评价。目前，运用区间DEA方法进行供应链合作伙伴评价研究的文献相对较少，特别是应用带有双重角色变量的区间DEA方法进行供应链合作伙伴评价的文献还没检索到。基于上述认识，本文研究带有双重角色变量的区间DEA供应链合作伙伴评价问题。

1 带有双重角色变量的区间CCR供应链合作伙伴评价模型

考虑一家供应链核心企业对n个供应链合作伙伴（比如供应商）进行评价的情形。候选合作伙伴投入m项的普通输入并得到s项的普通输出，并且存在c项既为输入又为输出的双重角色变量。任意候选合作伙伴j的普通输入向量为（若某些输入指标值是确定的，可将其理解为区间下界与上界相等的特殊区间值），其中为DMUj的第i项普通输入的区间值，对应的权重变量为vi，L和U分别表示区间值的下界和上界；普通输出向量为，其中为 DMUj的第r项普通输出的区间值，对应的权重变量为ur；双重角色变量向量为，其中为 DMUj的第k种双重角色变量的区间值，并有对应的输入权重变量Bk和输出权重变量rk。

据上述假设，就可以在Chen[4]提出的确定条件下带有双重角色变量的CCR模型基础上建立如下的带有双重角色变量的区间DEA供应链合作伙伴评价模型。

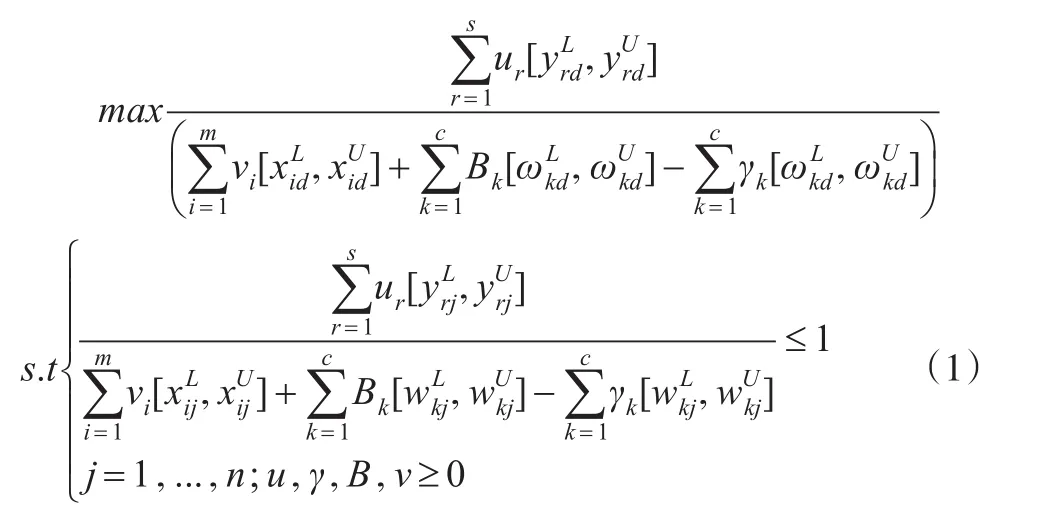
模型（1）是一个分式规划，运用C-C变换对其进行转换，得到等价规划模型如下：

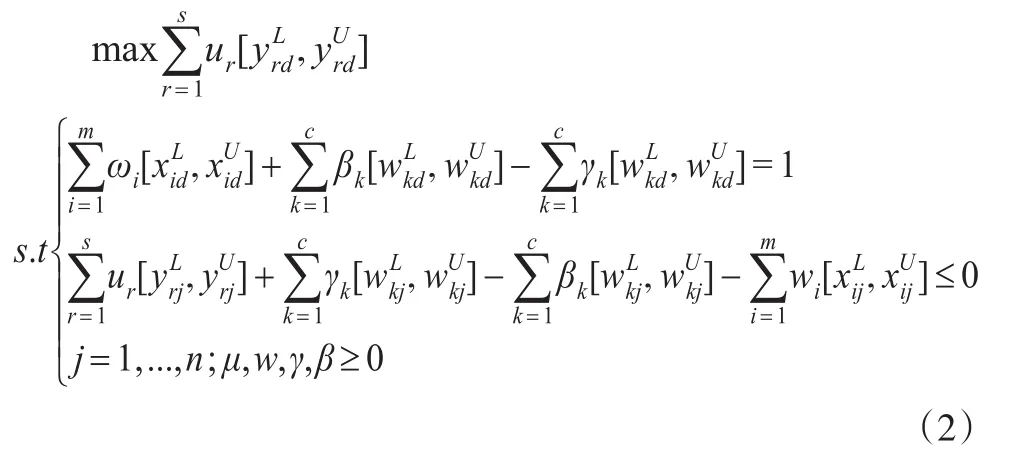
可以看出模型（2）是一个带有区间数的规划模型，无法直接进行求解。本文借鉴文献[5]的思想，通过构造最优参考集的方法来求解该模型。此时要构造最优参考集就是要使模型（2）的不等式约束的不等号左边各项之和最大化，即：

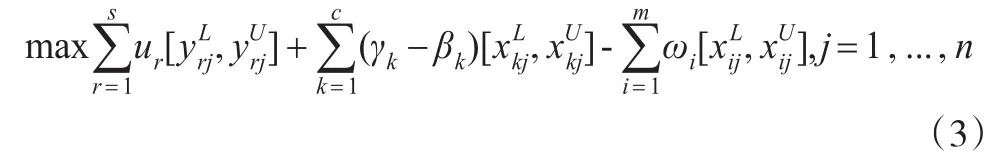
注意到μr，γk，βk，wi≥0是模型（2）的权重变量。明显地，在式（3）的各项中，普通输出的区间值应取最大值；普通输入的区间值应取最小值；双重角色变量区间值的部分无法直接取得最大值，需要进行进一步的讨论。此时式（3）转化为下式：

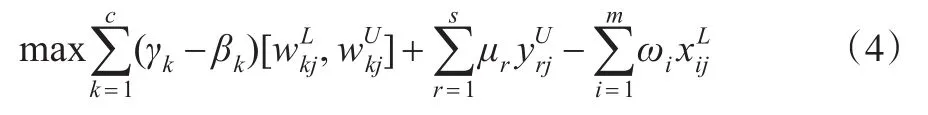
由于区间值非负，式（4）的最大值只与双重角色变量的输出权重与输入权重之差γk-βk有关。因此，接下来具体分析使式（4）取得最大值的情况。

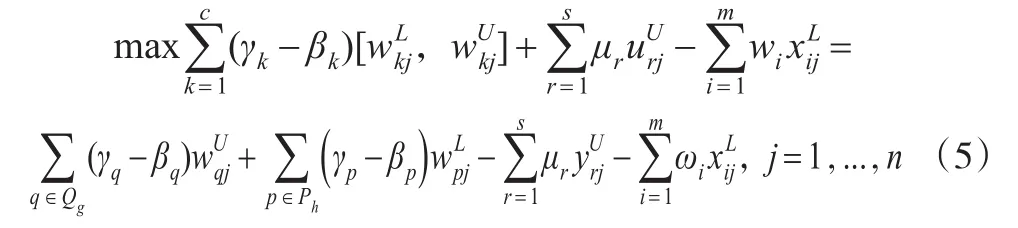
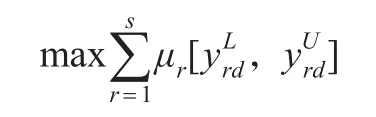
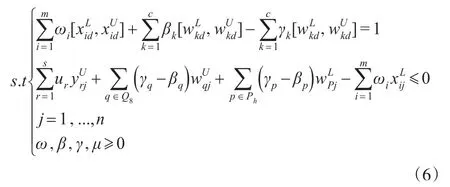
在上述分析中，对于权重变量γk和βk的取值分析是在事先对事后结果进行的假设。为保证在不同最优参考集下模型求解结果的有效性，事后求解的结果应与事前假设相符。因此，在模型（6）中必须加入以下权重约束条件以保证模型事后求解结果与事前假设的一致性：

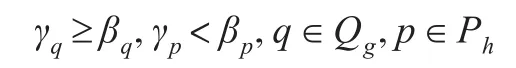
基于上述分析，可将模型（2）转化为能够在区间数条件下对带有多个双重角色变量的供应链合作伙伴进行评价的区间CCR模型：

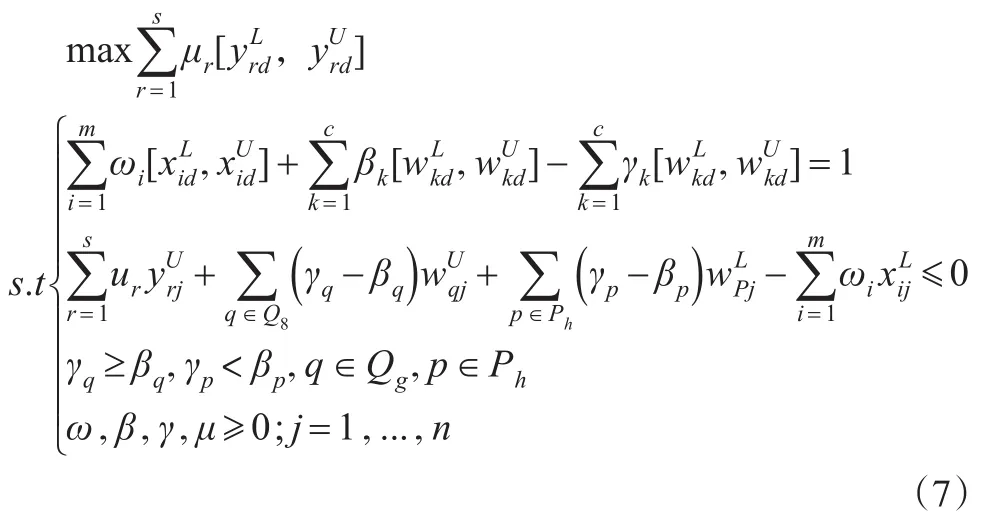
对于模型（7），要求得被评价单元DMUd的相对区间效率上界和下界，还需要进一步使被评价的DMUd分别处于最优和最劣的生产状态下。

区块链技术保证在不可信、分布式环境下，所有节点通过一定的共识算法对公共账本达成一致。在区块链中，账本以区块的形式构成，每个合法的区块都以特定的密码学方式链接到前一个块，这也就是区块“链”的内涵。随着区块的不断生成和添加，历史区块内容不能被修改，区块中记录的所有内容能够被网络中所有节点获取。

若被评价单元处于最优生产状态[5]，可由模型（8）求得它的区间效率上界值。

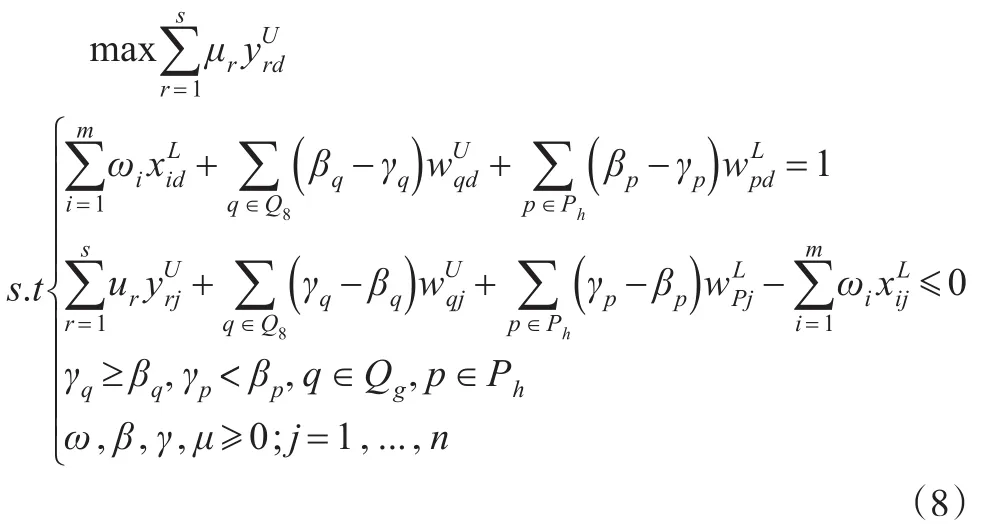
类似，若被评价单元DMUd处于最劣生产状态[5]，可由模型（9）求得它的区间效率下界值。

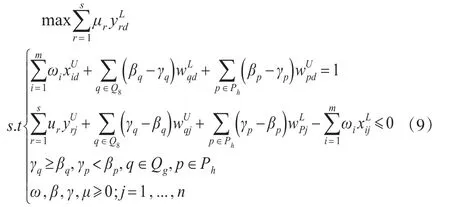
由于g和h的数值有多种可能的组合，所以求解模型（8）和模型（9）需要进行多次计算。可以按照以下步骤求解模型（8）以得到DMUd的区间效率上界值

第一步，在模型（8）中依次取g=0，g=1，...，g=c，相应地，h的取值为h=c，h=(c-1)，...，h=0，对于每个g和h的取值组合都有对应的最优参考集，模型（8）的约束条件也会相应地变化。g和h的所有取值组合共有个最优参考集及相应的约束条件，在每一组约束条件下求解模型（8）共能得到组最优权重解及对应每一组权重的目标函数值

第二步，为了尽可能使被评价单元的区间效率上界值最大，尽可能使信息丢失程度最小，取所有解得的最优权重中使目标函数值最大的那组权重作为最终所求的最优权重解，并将其表示为，这组权重得到的目标函数值就是DMUd的区间效率上界值，用表示解得这组最优权重时所使用的最优参考集，与该参考集对应的g的取值记为，h的取值记为，对应和的集合Qg和 Ph分别为

综上，通过上述步骤就可以求得区间数条件下带有双重角色变量的任意候选合作伙伴DMUd的区间效率。对于区间数的排序，国内外学者已经做了许多研究，比如可应用吴杰和梁樑[6]所提出的一种考虑所有权重信息的区间数排序方法进行排序。

2 模型算例

需说明的是，研发费用作为输入，对其他的产出有支持和改进作用，供应商通过投入资金到研发中，能够从降低成本和质量改进等多方面提高自身，对其他产出有积极意义；作为输出，研发费用保证了研究的质量和研究人员收入的质量，有效的研究开发和有保障的收入能促进供应商的研发项目能够继续良好进行[1]。供应商声誉是供应商在行业内的声誉水平，该指标作为输入，会提高员工的自豪感，对员工产生正向激励作用，促使员工自发地更有效率地工作，对其他产出有积极意义；作为输出，供应商的声誉水平向外界传递其综合实力的信息，良好的声誉能够减少核心企业在选择供应商作为合作伙伴时的不确定性，为供应商带来更多的业务，促使其更好的发展。

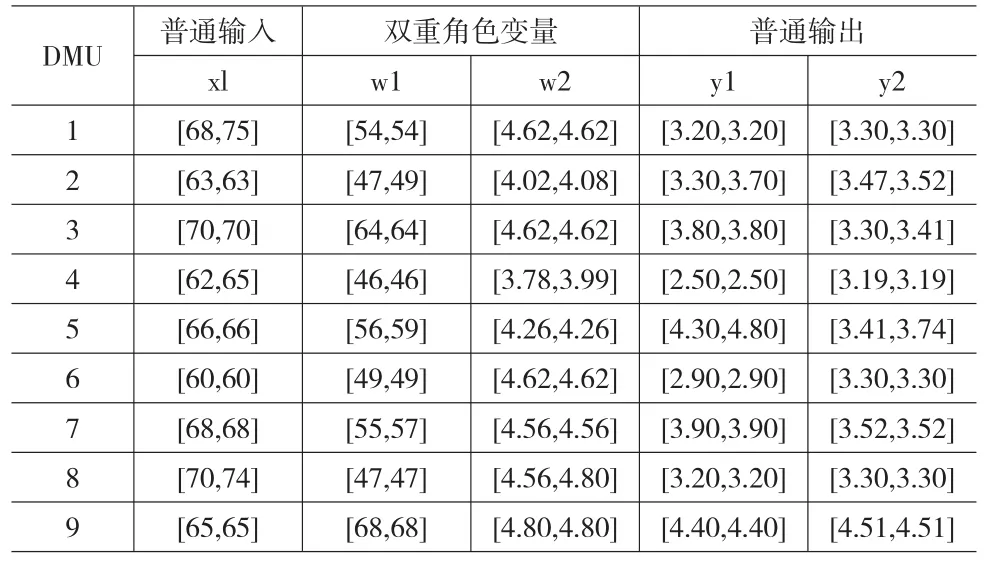
表1 候选合作伙伴的评价数据

根据表1的数据，可知m=1，s=2，c=2。由前文所提出的方法知，当C=2时，g和h的取值组合共有22=4种，此时式（5）有以下四种结果。

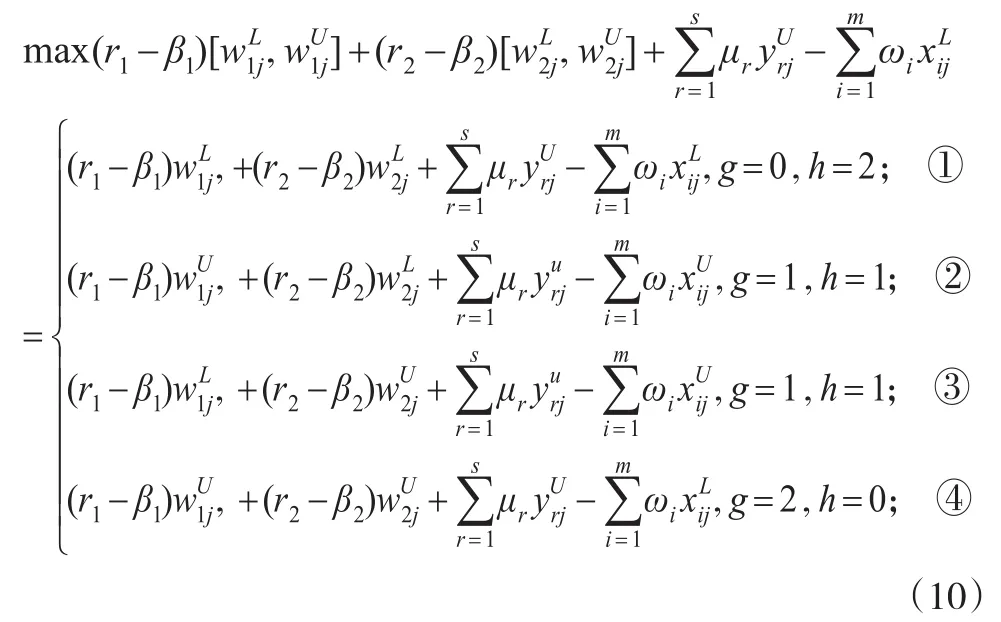
对应式（10）中①、②、③和④四种情况的最优参考集分别为，基于这四个最优参考集，根据表1的数据，在matlab2014环境下按照前文所述的方法应用模型（8）和（9）就可以对每个候选合作伙伴进行评价，得到的结果如表2所示。

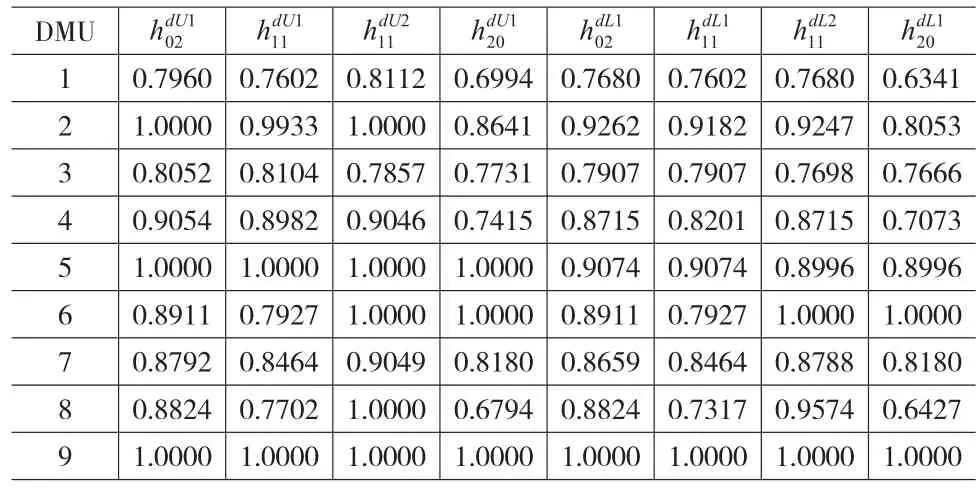
表2 最优参考集T021、T111、T112和T201下模型（8）和（9）的求解结果

根据表2的结果进行整理，可以得到如表3和表4所示的各候选伙伴的区间效率上下界值及对应的最优参考集。

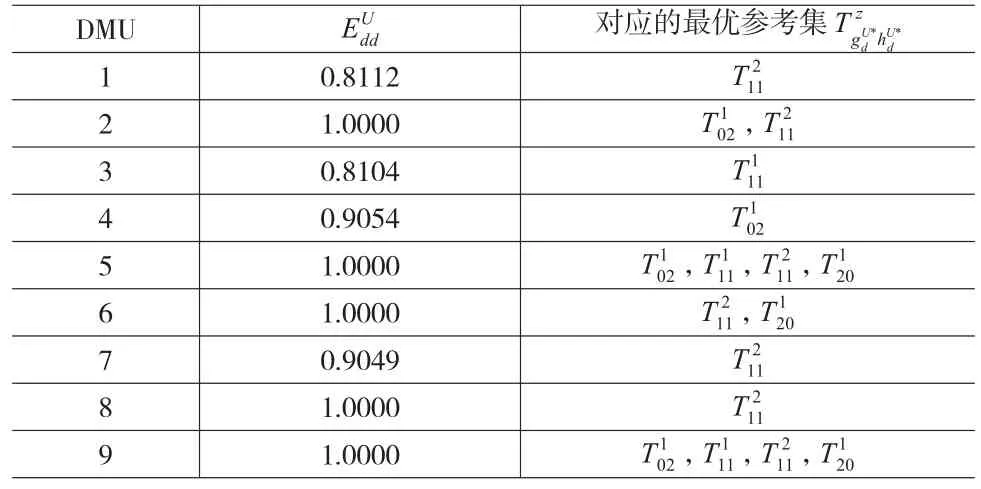
表3 各候选伙伴的区间效率上界值及对应的最优参考集

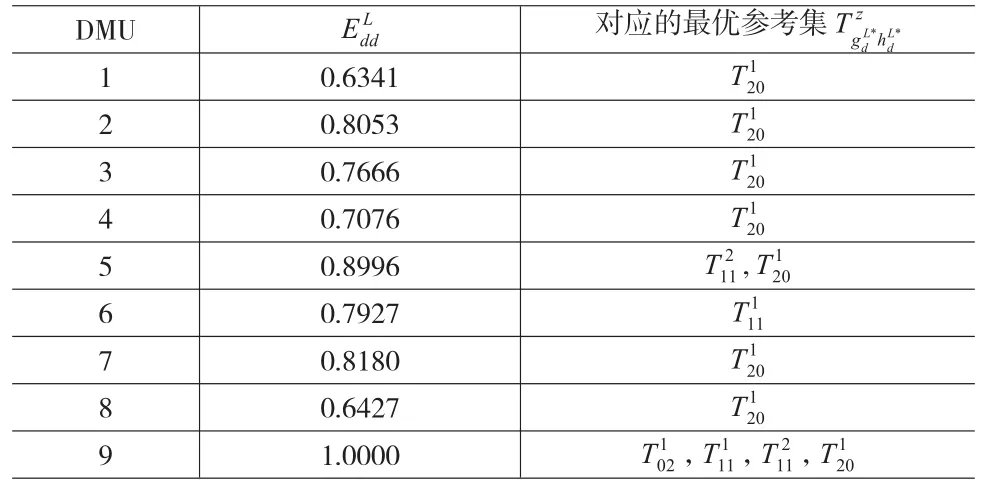
表4 各候选伙伴的区间效率下界值及对应的最优参考集

由表3和表4可得各单元的最终区间效率，如表5所示。

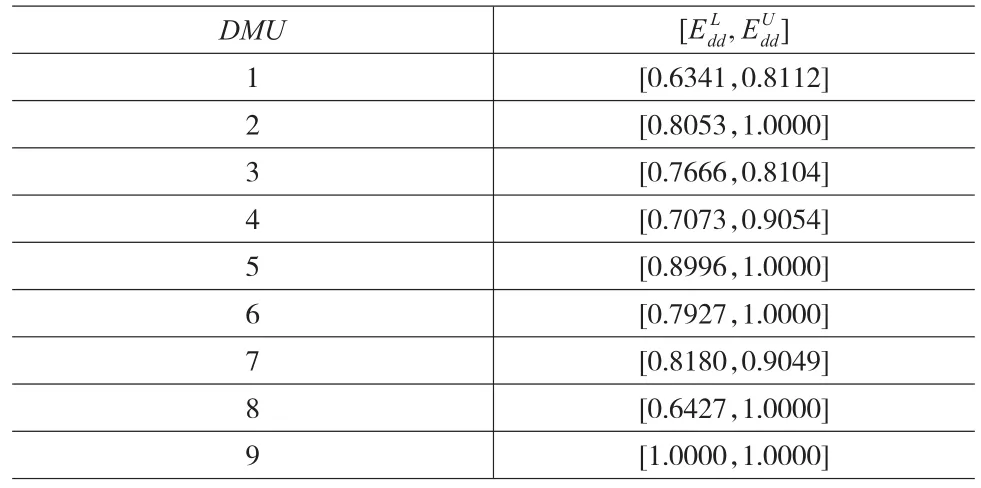
表5 各候选合作伙伴的区间效率

最后，需要对9名候选合作伙伴的区间效率进行排序，以便于核心企业进行选择。根据文献[6]提出的方法，按照表5的结果可以通过计算可能度矩阵并按行求和就可得到各候选合作伙伴区间效率的排序向量：

R=(1.0808，5.4707，2.2429，2.9967，6.9663，5.4861，4.5233，3.3337，8.500)T

按照该排序向量可以对各候选合作伙伴的区间效率值进行排序，结果为：

DMU9>DMU5>DMU6>DMU2>DMU7>DMU8> DMU4>DMU3>DMU1

根据该排序结果，供应链核心企业可以对候选合作伙伴进行选择（从好到差的顺序依次为合作伙伴9、5、6、2、7、8、4、3和1。

3 结语

本文在最优参考集的基础上构建了带有多个双重角色变量的供应链合作伙伴区间CCR模型，给出了模型的求解步骤。在今后，还可以从以下几个方面继续开展研究。

（1）对于非期望的双重角色变量的研究。由于双重角色变量的特殊性，其作用只有通过比较其输入和输出权重的大小才能确定，因此以往对非期望变量的处理方法无法直接用到双重角色变量上，对此需进一步研究。

（2）在不同的规模收益的假设前提下进行研究。在未来的研究中可以放宽规模报酬不变（CRS）的假设，研究规模报酬可变（VRS）下的带有双重角色变量的评价问题。

[1]Cook W，Green R，Zhu J.Dual-role Factors in Data Envelopment Analysis[J].IIE Transactions，2006，38(2).

[2]Noorizadeh A，Mahdiloo M，Farzipoor Saen R.Using DEA Cross-effi⁃ciency Evaluation for Suppliers Ranking in the Presence of Non-dis⁃cretionary Inputs[J].International Journal of Shipping and Transport Logistics，2013，5(1).

[3]Mahdiloo M，Noorizadeh A，Saen R F.A New Model for Suppliers Ranking in the Presence of Both Dual-role Factors and Undesirable Outputs[J].International Journal of Logistics Systems and Manage⁃ment，2013，15(1).

[4]Chen W C.Revisiting Dual-role Factors in Data Envelopment Analy⁃sis:Derivation and Implications[J].IIE Transactions，2014，46(7).

[5]Wang Y M，Greatbanks R，Yang J B.Interval Efficiency Assessment Using Data Envelopment Analysis[J].Fuzzy Sets and Systems，2005， 153(3).

[6]吴杰，梁樑.一种考虑所有权重信息的区间交叉效率排序方法[J].系统工程与电子技术，2008，(10).

（责任编辑/易永生）

N945

A

1002-6487（2016）21-0055-04

福建省软科学项目（2014R0054）

向小东（1973—），男，四川广安人，博士，教授，研究方向：管理科学与工程。