带优先级的单类型航空弹药转运多目标规划模型
杨 芸,李 彪,王帅磊
(海军航空工程学院,山东烟台 264001)
带优先级的单类型航空弹药转运多目标规划模型
杨 芸,李 彪,王帅磊
(海军航空工程学院,山东烟台 264001)
针对航母航空弹药转运过程非常复杂、涉及设备多、要求高的特点,在对其流程进行细致分析的基础上,将其抽象为一个两阶段多目标规划问题。同时,深入分析了转运过程中的各种约束条件、构建了该问题的两阶段优化模型。建模时,不仅考虑了武器升降机的有效利用、弹药量的合理分配等因素,还考虑了转运时对于不同类型弹药转运优先级与停机区弹药需求优先级的要求。通过模型优化,在满足转运优先级要求的基础上,能有效提高航空弹药的转运效率。
航空弹药;航母;优先级;多目标规划
航空弹药转运效率是影响航母舰载机出动架次率的重要因素[1⁃2]。随着技术的快速发展与战场要求越来越高,航母执行的任务越来越多样化。与之对应,舰载机挂载的弹药量越来越大、类型也越来越多,比如美“尼米兹”级航母舰载机所携挂的武器弹药量达到2470吨[3],F/A⁃18E/F“超级大黄蜂”在执行对地攻击任务时,通常携带4枚空中拦截导弹以及2~6枚对地攻击导弹/炸弹[4],因此,航空弹药转运效率成为制约航母作战能力的关键因素。
航母航空弹药转运问题十分复杂,不仅涉及多种设备的有效使用、人员的安排,还包括实际转运时的一些具体要求。文献[1,5]详细介绍了美“尼米兹”级航母的弹药转运系统与弹药转运流程,细致分析了航空弹药贮运的基本作业流程与各作业中遇到的问题,通过美新一级航母“福特”号与“尼米兹”级的对比,相应提出了的提高贮运效率的建议。文献[6]基于PERT技术,对航空弹药保障人员的优化配置进行了探讨。文献[7]构建了航空弹药转运的优化模型,并用遗传算法求解,但所建模型中没有考虑武器升降机的有效利用,假设条件也存在较大的局限性。
本文在详细分析航空弹药转运流程的基础上,将弹药转运问题抽象为两阶段多目标运输问题进行分析,构建了带优先级的弹药转运两阶段优化模型。该两阶段模型不仅考虑了弹药库中取弹量的合理分配、下/上层武器升降机的有效利用、各停机区所需弹药的快速运抵,还思考了实际应用中对于不同类型弹药的需求急缓程度以及不同停机区的弹药需求急缓程度。通过模型优化,能有效提高弹药的整体转运效率,各种设备也能得到有效利用。
1 航空弹药转运要求
1.1 注意转运安全
安全问题是转运过程中要特别注意的问题。在转运过程中,弹药本身容易损坏,若不认真固定好,可能出现弹药滑落与爆炸的情形。通常,甲板上任务较多、危险性高,弹药在甲板上的搬运尤其要注意安全。
1.2 提高转运效率
在保障转运安全的前提下,提升弹药转运效率是首要目的。转运效率的提升不仅能加快航母的快速反应能力,还有助于增强航母的作战能力。
1.3 提升设备利用率
转运设备利用率的提升,一方面在于提高弹药的转运效率,另一方面在于减少转运设备的使用次数,以降低航母能量的消耗与设备的故障率。
2 航母航空弹药转运流程与分析
在不考虑弹药库中弹药的倒换与拣选和弹药装配的情况下,可以将航母航空弹药转运流程分为两个阶段,分别如图1、2所示。
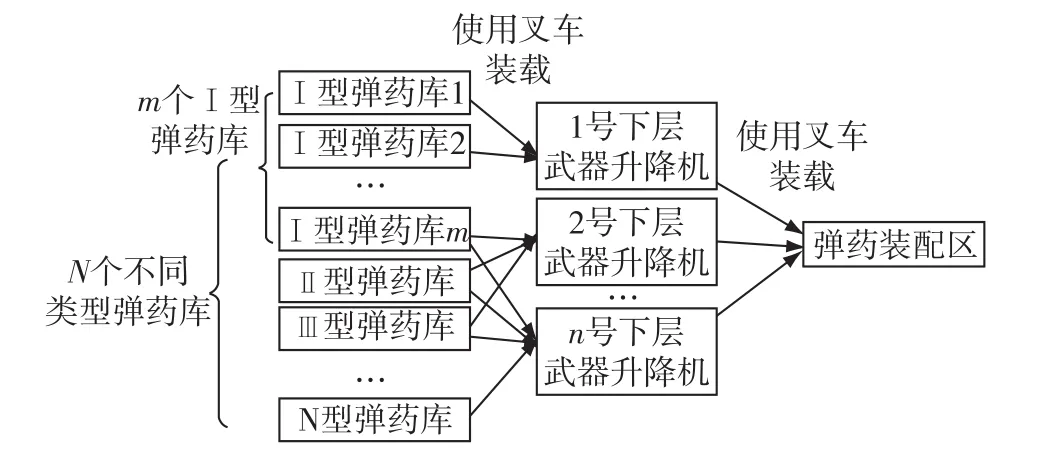
图1 航空弹药转运第一阶段流程图

图2 航空弹药转运第二阶段流程图
第一阶段,主要过程为弹药从弹药库搬运到下层武器升降机、下层武器升降机转运弹药。航母上有多个弹药库,同类型的弹药可能存放在不同弹药库中,同一个弹药库中还可能存储不同类型的弹药,因此,搬运前先要对不同弹药库的取弹量进行分配。另外,还需考虑下层武器升降机的装载量有限、不同弹药需求的急缓程度等。第二阶段,主要过程为上层武器升降机转运弹药、弹药从飞行甲板上搬运到各停机区。同样地,上层武器升降机的装载量有限,为了减少转运过程持续时间与甲板弹药搬运时间,需合理分配不同上层武器升降机的转运量与转运次数。
忽略掉一些细节,弹药转运问题与图3所示两阶段产销平衡运输问题十分相似。不同之处在于,弹药转运问题还涉及升降机的调度。对于运输问题与调度问题,理论的分析与求解方法的设计已较成熟[8⁃10],可以作为弹药转运问题分析、建模与求解的有益参照。

图3 两阶段产销平衡运输问题示意图
3 单类型航空弹药转运模型
本文中单类型弹药转运是指,在转运过程中武器升降机中只装载一种类型的弹药。在转运过程中,无需考虑武器升降机如何组合装载不同类型弹药最优。
3.1 模型的符号说明
R——飞行甲板上停机区总个数;
M——航母上储存的弹药类型总数;
Aα——航母上弹药库的总个数;
Mβ——上层武器升降机的总个数;
Mα——下层武器升降机的总个数;
Lλ——可能需要的弹药运输车总数;
Lα——下层武器升降机可能的最大转运趟数;
Lβ——上层武器升降机可能的最大转运趟数;
i——飞行甲板停机区编号,1≤i≤R;
j——航母上存储的弹药类型的编号,1≤j≤M;
r——上层武器升降机的编号,1≤r≤Mβ;
k——航母上弹药库的编号,1≤k≤Aα;
o——下层武器升降机的编号,1≤o≤Mα;
t——弹药运输车的编号,1≤t≤Lλ;
u——下层武器升降机转运顺序号,每部下层武器升降机从弹药库抵达弹药装配区一次算一趟,1≤u≤Lα;
v——上层武器升降机转运顺序号,每部上层武器升降机从弹药装配区运抵飞行甲板一次算一趟,1≤v≤Lβ;
nu——下层武器升降机第u趟转运时从弹药库中取出的弹药数量;
qj——j类型弹药的优先级,分为三个等级;
pi——表示第i个停机区的弹药需求优先级,分为四个等级;
Nij——第i号停机区所需的j类型弹药的数量;
Gk——第k号弹药库中存储的弹药总量;
T1k——下层武器升降机从k号弹药库到达弹药装配区的时间;
T2——上层武器升降机从弹药装配区抵达飞行甲板的时间;
Turi——从r号上层武器升降机舱口搬运一趟弹药到i号停机区消耗的时间;
Dwj——下层武器升降机对于j类型弹药的最大装载量;
Cj——依据弹药类型设定的常数,弹药在存储与转运过程中可能出现损坏,实际取弹时,一般需要根据弹药类型的不同而对实际的取弹量进行调整;
Udt——t号弹药运输车上装载的弹药量;
Uutj——t号弹药运输车上可装载的最多的j类型弹药数量;
Wuj——上层武器升降机可装载的j类型弹药运输车数(车上不装载弹药时);
Wdj——上层武器升降机可装载的j类型弹药数。
3.2 处理流程
弹药转运问题实质上是一个带约束的两阶段多目标规划问题。建模时,通过对弹药转运流程中各部分进行优化,先使得所需弹药转运所耗费的总时间最少,即效率最高,再要求各种设备和人力资源的使用量尽可能少,即成本最低。图4给出了具体的处理流程。
3.3 约束条件分析
由于航母弹药库、武器搬运人员等资源和武器升降机、弹药运输车等设备的数量有限,航空弹药转运过程不可避免地会受到这些条件的约束,深入分析这些约束条件是提升航空弹药转运效率与构建优化模型的基础。
3.3.1 弹药库
航母的弹药库主要包括专用弹药库和多类型弹药库[11]。大部分弹药库是专用弹药库,只储存一种型号的弹药。文中建模时,只考虑从专用弹药库中取弹的情形。对于多类型弹药库中取弹,可以与弹药贮存问题联合进行考虑,将其转化为专用弹药库取弹问题,比如运用情景感知计算[12],借助物联网、计算机等方面的先进技术,重新设计并改造弹药库,使其能自动根据不同情景调整弹药库中弹药的位置与不同位置的存放数量,实现弹药的自动拣选与倒换[13]。
记符号Xuk、Skj为,

则从弹药库中取弹的约束条件为:
1)取出的某类型弹药量等于该类型弹药需求量加调整量,
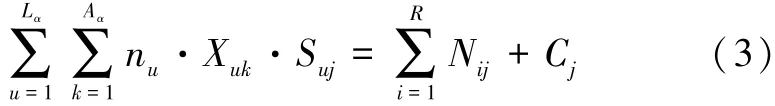
2)某个弹药库中的取弹量不得超过该弹药库中的存储总量,

3)单趟取弹数量不得超过弹药库中的存储总量,

4)限定每趟只从一个弹药库中取弹,

5)限定每趟只取一种类型的弹药,

3.3.2 武器升降机
武器升降机是航空弹药转运过程中非常重要的舰上设备。合理规划每部升降机的载运量与载运次数,是提升弹药转运效率的关键。
通常,航母上包含两种类型的升降机,下层武器升降机和上层武器升降机。下层武器升降机负责弹药库与弹药装配区之间的弹药转运,上层武器升降机负责将装配好的弹药从弹药装配区转运到飞行甲板。对于不同级别的航母,由于武器装配区位置的不同,使得升降机转运的距离也存在差异。图5给出了美“尼米兹”级和“福特级”航母的航空弹药转运过程。
对于下层武器升降机,记符号Zuo为,

则转运时的约束条件为:
1)每趟转运量不得超过升降机的最大载运量,

2)每趟只使用一部下层武器升降机,

3)可能转运次数不得超过转运次数上限(每次只转运一颗时对应的次数),
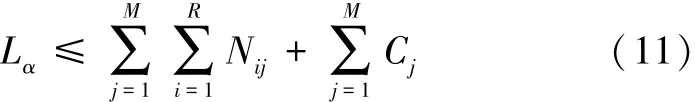

图4 航空弹药转运问题的处理流程
对于上层武器升降机,记符号svt,zvr,ytj为,

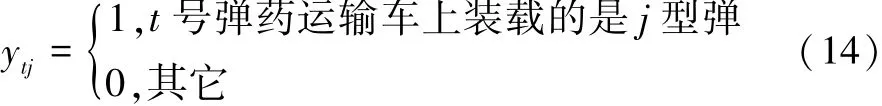
则转运时的约束条件为,
1)每趟转运弹药量不得超过升降机的最大运载量,

2)每趟转运弹药运输车数不得超过升降机的可装载数,


图5 美航母航空弹药转运示意图
3)每趟只使用一部武器升降机,

4)每趟只转运一种类型的弹药,

5)可能的转运次数不得超过转运次数上限(每次只转运一颗时对应的次数),

3.3.3 弹药运输车
在航空弹药转运的第二阶段,弹药是固定在弹药运输车上进行转运的。对于某些大型的弹药,受弹药运输车运载能力的限制,运输车只能装载一颗;对于小型的弹药,则可以装载多颗。建模时,这是两种完全不同的情况,后者不仅要考虑上层武器升降机能装载多少辆运输车,还需要考虑运输车上装载多少颗弹药以及弹药如何分发到停机区。文中仅对“一车多弹”情形进行建模,“一车一弹”可视为“一车多弹”的特例。
记符号xti为,

则对应的约束条件为,
1)每辆运输车的装载量不得超过运输车的最大载量,

2)运往停机区的某型弹药量需等于该停机区的需求量,

3)单辆运输车上装载的运往某停机区的弹药量不得超过该停机区的需求量,

4)每辆运输车上只装载一种类型的弹药,

5)每辆运输车只运往一个停机区,

6)可能的弹药运输车数不得超过需求上限(每辆只装载一颗时对应的数量),

3.3.4 不同类型弹药的优先级要求
战场形势变化快、航母执行的任务多样,不同时刻舰载机所需的不同类型弹药的急缓程度不同。受武器升降机载运能力、运输人员搬运效率等限制,所需航空弹药只能按批次进行转运。因此,需要划定不同时刻不同类型弹药的转运优先级。本文将不同类型弹药的优先级分为三个级别,“急需”、“需要”、“不需要”,分别对应于数字“2”、“1”、“0”。
在转运时,约定先转运优先级高的弹药类型,即

3.3.5 不同时刻停机区弹药需求优先级要求
受各停机区舰载机起飞准备效率、各停机区规划的舰载机起飞数量等因素的影响,不同时刻,各停机区待起飞的舰载机数量不同,从而使得停机区弹药需求的急缓程度不同。上层武器升降机载运能力有限,弹药只能按批次运抵飞行甲板,再进行分发。因此,弹药转运时,需要考虑各停机区弹药需求的优先级。本文用数字“3”、“2”、“1”、“0”分别表示各停机区弹药需求的优先级,对应为“非常急”、“急”、“不急”、“无需求”。
在转运时,约定先满足优先级高的停机区的弹药需求,即

3.4 模型构建
航空弹药装运问题作为一个二阶段多目标规划问题建立模型可以分两个阶段。
3.4.1 第一阶段转运模型
第一阶段,在不考虑弹药搬运时间与搬运人员优化配置的情况下,下层武器升降机就成为了影响弹药转运效率最大的因素。要求目标函数为,在转运时间持续最长的下层武器升降机的持续时间最小的同时,所有下层武器升降机总的转运时间最短。
因此,第一阶段转运模型为,
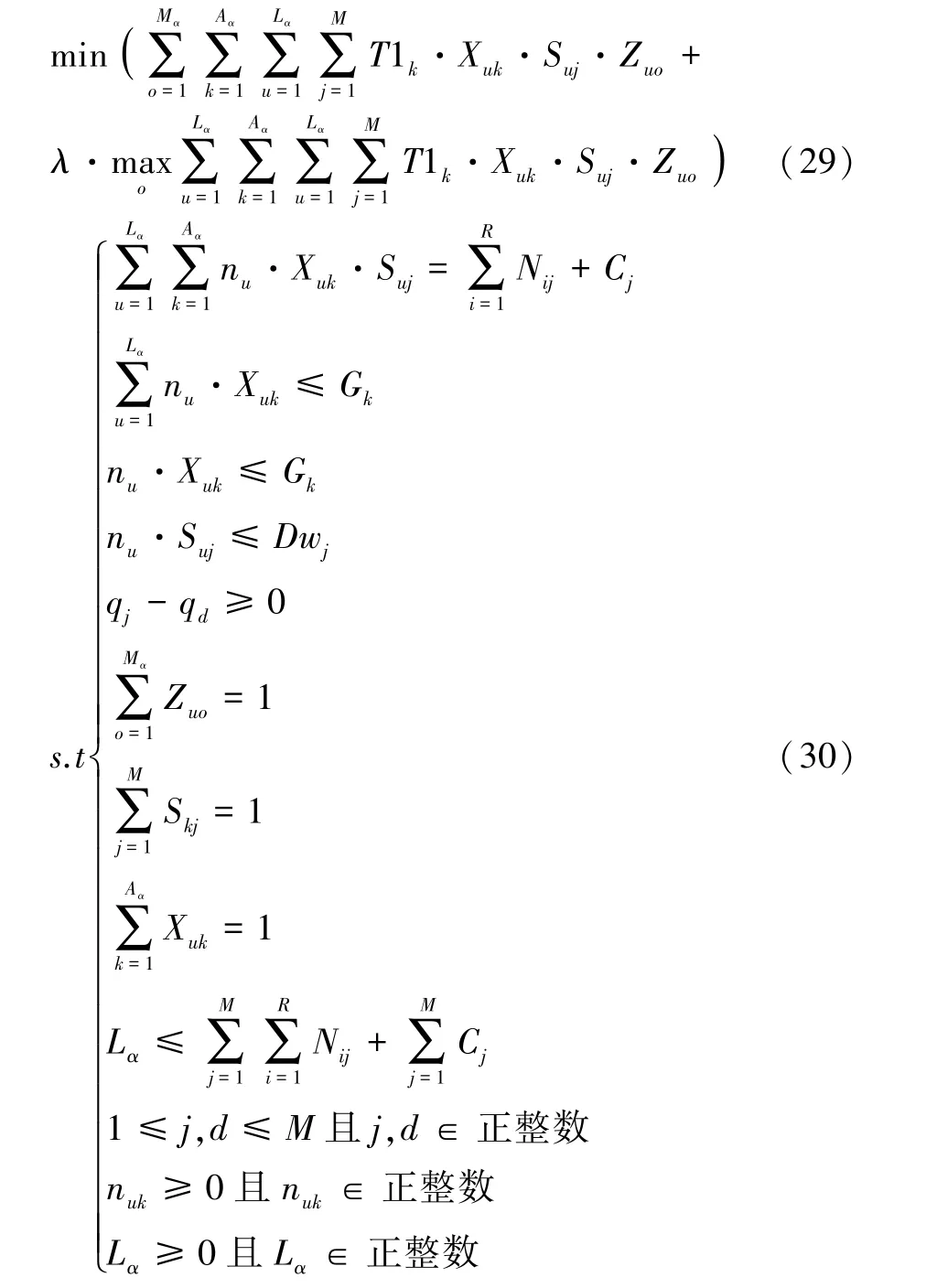
式(29)中,λ为权重系数。需注意的是,所建模型中暗含了一个条件,即每次从弹药库中取出的弹药量等于下层武器升降机每趟运载的弹药量。
为了使第一阶段转运过程中成本最低,在式(29)、(30)的基础上,进一步要求模型所求得的解满足下层武器升降机总的转运次数最少,即minLα。
3.4.2 第二阶段转运模型
对于第二阶段,由于不涉及弹药在上层武器升降机中的组合运输,若想使转运效率最高,只需考虑在满足停机区弹药需求优先级的前提下,使各停机区所需弹药在飞行甲板上的搬运总时间最短、上层武器升降机的转运次数最少。在该模型中,一辆弹药运输车上允许装载多颗弹药。
因此,可建立如下所示模型,

式(31)中,γ为权重系数。
为了使第二阶段转运过程中成本最低且上层武器升降机的转运持续时间较短,在式(31)、(32)的基础上,进一步要求最终解满足上层武器升降机总的转运次数与弹药运输车的使用数量两者最少,即minLβ+ Lλ。
4 结束语
航空弹药的转运效率直接影响到舰载机的出动架次率,从而影响航母的整体作战能力。航空弹药的转运过程十分复杂,只有合理安排转运流程中的各任务工序、高效利用转运设备,才能有效提升转运效率。本文在对航空弹药转运流程进行分析的基础上分析了转运过程中各种约束条件,构建了航空弹药转运两阶段模型,对弹药转运流程中各任务工序进行了合理的规划,提高了转运设备的利用率,对弹药转运效率的提升有较大的帮助。
后续,将在本文的基础上构建多类型航空弹药转运模型,并设计具有Levy飞行特征的双子群变异遗传算法与扫描法结合对模型进行求解。
[1] 史文强,李彦庆,陈练.航空母舰飞行甲板作业及弹药转运系统分析[J].中国舰船研究,2012,7(3):9⁃14.
[2] 陈和彬.隐藏的战力航母舰载机武器弹药转运挂载深度透析[J].航空世界,2014(11):48⁃53.
[3] 鸥汛.航母的升降机装置[J].现代舰船,2005(10):40⁃43.
[4] 史文强,陈练,蒋志勇.航母航空弹药组成及需求分析[J].舰船科学技术,2012,34(5):139⁃143.
[5] 史文强,李彦庆,陈练.航母的航空弹药贮运作业解析[J].舰船科学技术,2013,35(6):136⁃141.
[6] 郭小威,马登武,邓力.基于PERT网络的航空弹药保障人员优化配置[J].北京航空航天大学学报,2014,4(1):69⁃74.
[7] 曲晓燕,温德宏,谢勇.遗传算法在舰载机弹药转运任务优化配置中的应用[J].计算机与现代化,2012(3):23⁃26,29.
[8] 郭海湘,杨娟,於世为,等.带服务优先级的煤矿物资配送车辆路径问题[J].系统管理学报,2012,21(1):133⁃144.
[9] 韩世莲,刘新旺.多目标多模式模糊运输问题的最优折衷解[J].系统工程,2007,25(9):26⁃32.
[10]王旭,葛显龙,代应.基于两阶段求解算法的动态车辆调度问题研究[J].控制与决策,2012,27(2):175⁃181.
[11]GOSHORN P C.Aviation ordnanceman[R].Naval Edu⁃cation and Training Professional Development and Tech⁃nology Center,2001.
[12]童恩栋,沈强,雷君,等.物联网情景感知技术研究[J].计算机科学,2011,38(4):9⁃14,20.
[13]赵晓春.美国航母弹药库自动化贮运技术发展及应用分析[J].舰船科学技术,2013,35(8):154⁃157.
Multi⁃objective Programming Model to Single Type of Air Ammunition Transfer with Priority Level Constraints
YANG Yun,LI Biao,WANG Shuai⁃lei
(Naval Aeronautical and Astronautical University,Yantai 264001,China)
According to the process of ammunition transfer's characteristic which is very complex and related to a lot of e⁃quipment and has high requirements,this paper regarded it as a two⁃stage multi⁃objective programming problem based on a detailed analysis of its procedure,and in⁃depth analyzed a variety of constraint conditions and constructed a two⁃stage optimi⁃zation model to this problem.The model not only considered effective use of weapons elevators and reasonable distribution of ammunitions,but also considered demand of priority level constraints to different types of ammunition and ammunition re⁃quirements of parking area.Through the model's optimization,the transfer efficiency of air ammunition can get effectively im⁃proved and meet the priority level constraints of transfer.
air ammunition;aircraft carrier;priority level;multi⁃objective programming
TP273;E911
A
10.3969/j.issn.1673⁃3819.2016.06.010
1673⁃3819(2016)06⁃0046⁃07
2016⁃08⁃12
2016⁃09⁃18
杨 芸(1991⁃),男,湖南桃江人,硕士研究生,研究方向为离散事件动态系统,机器学习。
李 彪(1962⁃),男,副教授,硕士生导师。
王帅磊(1991⁃),男,硕士研究生。

