煤炭可选性曲线数学模型的建立与应用
郭 德,陈国玉,孙 娜,曹 辉
(华北科技学院 环境工程学院,北京 101601)
煤炭可选性曲线数学模型的建立与应用
郭 德,陈国玉,孙 娜,曹 辉
(华北科技学院 环境工程学院,北京 101601)
为了探索出一种简单、实用的煤炭可选性曲线数学模型,基于分形理论建立累计灰分与分选密度数学模型,并通过多项式拟合建立累计产率与累计灰分数学模型,两个数学模型联合应用可替代可选性曲线,用于计算重力选煤过程中的各项理论分选指标,这对于直接计算选煤理论指标有着重要意义。
分形理论;可选性曲线;数学模型;理论分选指标
煤炭可选性曲线是由煤炭密度组成的图示,反映了其质与量的关系,通常用于判断煤炭的可选性,解决选煤工艺中的理论工艺指标和分选条件等问题。作为分析煤炭可选性和获得理论分选指标的一种手段,煤炭可选性曲线在选煤生产和设计中具有非常重要的作用。煤炭可选性曲线有两种,即H-R曲线和M曲线,最常用的为H-R曲线。但这些可选性曲线在绘制与应用过程中存在一些不足,根据原煤浮沉试验资料绘制可选性曲线时,不但绘制过程繁琐,而且不够准确,也不易实现计算机处理,导致可选性曲线所查指标与后续的工艺数质量计算结果不能完全匹配。
现有的煤炭可选性曲线数学模型主要包括反正切模型、双曲正切模型、复合双曲正切模型[1],而这些模型中各参数的物理意义不明确,获取曲线参数和直接计算各工艺指标均比较麻烦,有必要建立一种简单、实用的煤炭可选性曲线数学模型。为此,在对分形理论和累计产率与累计灰分关系研究的基础上,探索性地建立了一种物理意义明确,且应用简单的可选性曲线数学模型,并结合实际数据阐述了该模型的应用方法。
1 煤炭可选性曲线数学模型的建立
1.1 分形理论
分形几何学由法国数学家Mandelbrot B B于上世纪80年代初创立[2-3],具有自相似性和标度不变性的系统称为分形系统[4],分形理论主要研究内容是具有自相似性的不规则曲线和位线、具有自反演性的不规则图形、具有自平方性的分形变换及具有自仿射的分形集等[5]。分形维数简称分维,是描述分形的数量特征的主要参数,用于度量复杂形体的不规则性,也可以揭示复杂现象中深藏的有组织结构[6-7],该理论在物理化学、材料科学、信息科学、岩土、地质等领域应用十分活跃。
1.2 累计灰分与分选密度的数学模型
近年来,分形理论在一些领域得到了广泛应用。累计灰分与密度的关系符合分维特性,通过分形理论可以精确地反应累计灰分与分选密度的数学关系。分形分布可采用幂指数分布定义为:

(1)
式中:r为特征线度;N为与r有关的数量;C为待定常数;D为分维数。
累计灰分与分选密度的关系见下式:
A=f(δ),
(2)
式中:A为累计灰分,%;δ为分选密度,g/cm3。
如果将其转换为变维分形模型,可得

(3)
联立式(2)与式(3)可得:

(4)
分维数D为:

(5)
分维数D可以统一写为如下幂级数形式:
D=a0+a1δ+a2δ2+……+anδn,
(6)
根据式(2)可以计算出若干个已知数据组,结合式(3),通过求解方程组来确定变维分形模型。将式(6)带入式(3)后,对等式两边同时取对数,可得:
lnA=C1-(a0+a1δ+a2δ2+……+anδn)lnδ,
(7)
C1=lnC。
式(7)是关于n个未知数的线性方程组,将n个已知数据组的坐标代入其中求解线性方程组,即可确定变维分形模型的各个参数[8-9]。
现以表1中的0.5~50 mm粒级煤炭浮沉试验综合数据[10]为例,进一步说明累计灰分与分选密度的数学模型建立过程。
将表1中的累计灰分与分选密度代入式(7),可得:C1=-3.941 8,a0=-79.814 7,a1=66.371 0,a2=-15.576 8,则有
lnA=-3.941 8-(-79.814 7+
66.371 0δ-15.576 8δ2)lnδ,
(8)
由式(8)可推算出A值,

(9)
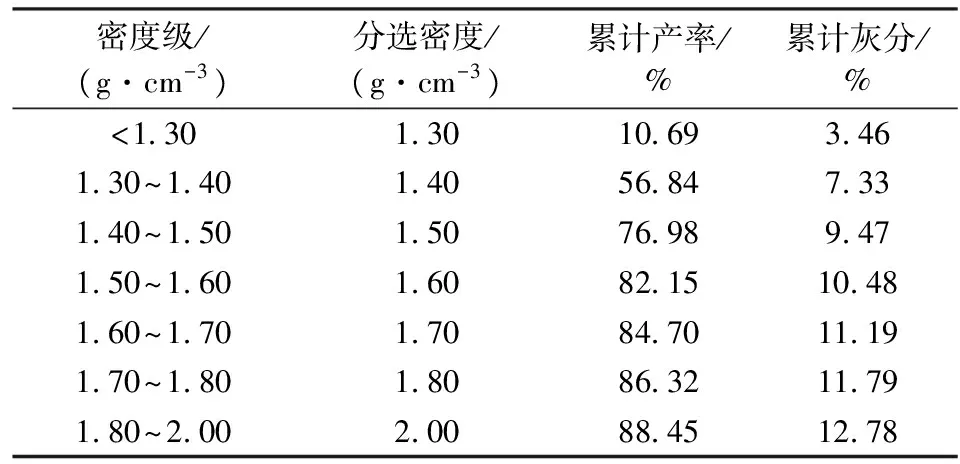
表1 0.5~50 mm粒级煤炭浮沉试验综合表
式(9)即为所建的累计灰分与分选密度数学模型,为验证模型的精确性,将实际浮沉灰分与模型计算灰分进行对比,结果如表2所示。
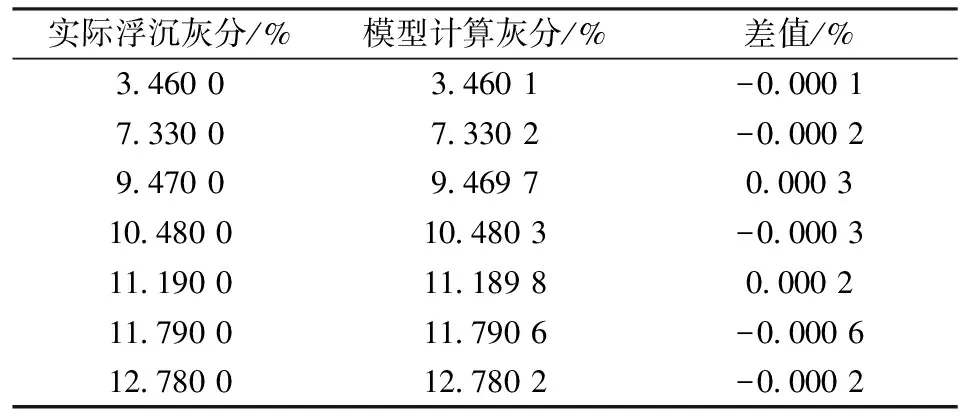
表2 实际浮沉灰分与模型计算灰分对比结果

1.3 累计产率与累计灰分的数学模型
研究发现,累计产率与累计灰分、分选密度与累计产率之间不存在显著的分维特性,故不能采用分形理论建立二者之间的数学模型。在对大量资料统计的基础上发现,累计产率与累计灰分之间的关系可以用多项式表达,具体表达式为:
γ=aA3+bA2+cA+d,
(10)
式中:γ为累计产率,%;A为对应的累计灰分,%;a、b、c、d为关系式的系数。
以表1中的数据为例,所建的累计产率与累计灰分数学模型为:
γ=0.024 1A3-1.310 5A2+
24.517 0A-59.829。
(11)
R2是拟合程度的指标,其数值大小可以反映估计值与对应的实际数据之间的拟合程度,拟合程度越高,可靠性就越高。当R2等于1或接近1时,可靠性最高;反之,可靠性较低。式(11)的R2为0.998,说明所建数学模型的精度很高。
2 数学模型的应用
根据式(9)和式(11),可方便地求出煤炭各项理论分选指标,并判断煤炭的可选性。现以表1数据为例,说明两个模型相结合的具体应用方法。当要求精煤灰分为10%时,由式(9)可求出原煤理论分选密度为1.52 g/cm3,根据式(11)得到的精煤理论产率为78.39%。
2.1 计算分界灰分
设δ1为比理论分选密度低0.01 g/cm3的密度、δ2为比理论分选密度高0.01 g/cm3的密度、A1为与δ1对应的累计灰分、A2为与δ2对应的累计灰分、r1为与A1对应的累计产率、r2为与A2对应的累计产率、Δr为r1、r2两个产率之差、λ为边界灰分。λ的具体计算方法为:
(1)由于理论分选密度为1.52 g/cm3,故δ1=1.51 g/cm3、δ2=1.53 g/cm3时,根据式(9)计算出的A1=9.83%、A2=10.20%;根据式(11)计算出的对应产率r1=77.43%、r2=79.48%;
(2)依据Δr=r2-r1,可得出Δr=2.05%;根据r1A1+Δrλ=r2A2,结合上述相关数据可得出λ=24.18%。
2.2 计算δ±0.1含量
设r-2.0为<2.00 g/cm3密度级的产率、r1.62为比分选密度1.52 g/cm3高0.10 g/cm3密度级对应的产率、r1.42为比分选密度1.52 g/cm3低0.10 g/cm3密度级对应的产率、r±0.1为δ±0.1含量。δ±0.1含量的具体计算方法为:
(1)当分选密度为2.00 g/cm-3时,根据式(9)可计算出对应的灰分为12.93%,通过式(11)可计算出r-2.0=90.18%。

当要求的矸石分选密度已知时,采用式(9)和式(11)即可求出精煤和中煤的数质量,也能求出相应的矸石的数质量。
3 结论
(1)通过分形理论和多项式拟合建立了累计灰分与分选密度、累计产率与累计灰分的数学模型,该建模方法简单,物理意义明确。
(2)应用实例说明,两个数学模型联合应用,不仅便于确定重力选煤的各项理论分选指标,还能有效判断煤炭的可选性,且进一步验证了模型的准确性和实用性。
[1] 匡亚莉.选煤厂管理[M].徐州:中国矿业大学出版社,2011.
[2] 高安秀树.分数维[M].沈步明,常子文,译.北京:地震出版社,1989:1-30.
[3] 郝柏林.分形与分维[J].科学杂志,1985,38(1):9-17.
[4] 吴安泽.基于分形理论的路基填石料粒径优劣分析[J].山西建筑,2014,40(24):71-72.
[5] 刘松玉,方 磊,陈浩东.论我国特殊土粒度分布的分形结构[J].岩土工程学报,1993,15(1):23-30.
[6] 薛祥立.粒度分布函数的分形表示[J].青岛建筑工程学院学报,1997,18(4):81-82.
[7] 付玉珠.填石路基大粒径填料特性试验研究[D].成都:西南交通大学,2013.
[8] 付煜华,付安捷.用分形模型统一各种油气田产量预测模型[J].新疆石油天然气,2009,5(1):47-50.
[9] 丁 浩,鲍 雨.基于分形理论的我国碳排放量预测研究[J].河南科技,2014,32(9):1815-1820.
[10] 谢广元.选矿学[M].徐州:中国矿业大学出版社,2001.
Development and application of the coal washability-curve mathematical model
GUO De, CHEN Guo-yu, SUN Na, CAO Hui
(College of Environmental Engineering, North China Institute of Science & Technology, Beijing 101601, China)
To simple yet practical coal washability-curve mathematical models have been developed. One is the fractal theory-based cumulative ash-separating density model while the other is the cumulative yield-cumulative ash model established through polynomial fitting. When used in combination, the 2 models can replace the washability curve for calculating the various theoretical separation indices in coal gravity separation process. This is of great significance for the direct estimation of theoretical indices in coal separation.
fractal theory; washability curve; mathematical model; theoretical separation indices
1001-3571(2016)01-0001-03
TD94
A
2016-01-30
10.16447/j.cnki.cpt.2016.01.001
郭 德(1964—),男,山东省成武县人,教授,从事矿物加工工程方面的教学与科研工作。
E-mail: guode@ncist.edu.cn Tel: 13785657868

