外包花纹钢-混凝土组合梁弹性受弯性能

陈丽华, 陈雷飞, 屈 创, 徐如楠

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)



外包花纹钢-混凝土组合梁弹性受弯性能

陈丽华, 陈雷飞, 屈 创, 徐如楠

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

文章提出了一种外包花纹钢-混凝土压型钢板组合梁,为研究其滑移影响下的弹性受弯性能,进行了6根足尺外包钢-混凝土简支组合梁的静力加载试验。对试件的荷载-滑移曲线和荷载-挠度曲线进行分析,探讨了抗滑移连接度对组合梁变形发展规律的影响;并根据是否考虑滑移效应分别推导出相应的弹性承载力计算公式。研究结果表明:随着抗滑移连接度的降低,试件的抗弯承载力和延性均随之降低;当不考虑滑移效应影响时,弹性承载力试验值与理论值比值的均值为0.92,计算结果偏于不安全；考虑滑移效应影响后,试验值与理论值比值的均值为1.02,计算结果偏于安全，且与试验结果吻合度较高。

外包花纹钢-混凝土压型钢板组合梁;弹性承载力;滑移;理论计算

外包花纹钢-混凝土压型钢板组合梁是采用花纹钢板直接冷弯成C型截面,然后将压型钢板用螺栓固定在C型钢梁上翼缘、在C型钢梁的梁肋内以及压型钢板面层整体浇筑混凝土而形成,试件的截面构造如图1所示。

该组合梁构造形式简单,外包钢板兼具受力与充当模板的作用,且钢板内表面带有凸起的扁豆型花纹可以增强钢和混凝土之间黏结力,减少抗剪连接件数量,方便施工,缩短施工周期,可实现产业化生产,加快钢结构住宅产业化的进程。

对于直接承受动力荷载作用或正常使用极限状态下的结构,必须采用弹性方法进行组合梁受力性能的分析验算。

为研究外包花纹钢-混凝土组合梁的弹性受弯性能,本文在6根外包花纹钢-混凝土组合梁试验结果的基础上,探讨抗滑移连接度对组合梁变形发展规律的影响,考虑交界面滑移引起的附加弯矩,对采用换算截面法计算的组合梁弹性承载力进行修正,以期定量地得出滑移效应对组合梁弹性承载力的影响。

图1 试件截面示意图

1 试验概况

本试验考虑钢梁宽度、螺栓布置、纵筋布置、剪跨段长度等主要参数,制作了6根计算跨度均为3.4 m长的外包花纹钢-混凝土组合梁。其中SCB-1、SCB-2为完全抗滑移连接组合梁,SCB-3～SCB-6为部分抗滑移连接组合梁。

试件主要设计参数见表1所列,部分材料的主要力学性能见表2所列。

表1 试件设计参数

表2 部分材料的力学性能

因试件采用商品混凝土且分2次浇筑,导致2批次混凝土实测强度有所不同,SCB-1、SCB-2为第1批次混凝土浇筑,SCB-3～SCB-6为第2批次混凝土浇筑。第1批次与第2批次混凝土抗压强度均值分别为18.54、16.74 MPa。试验试件的外包花纹钢梁采用花纹钢板加工而成,目前扁豆形花纹钢板在市场上最为常见,为方便推广,本试验选用扁豆形花纹钢板,如图2所示。

本试验6根简支组合梁全部采用2点对称加载,加载装置如图3所示。试验过程中,采用同步加载,在外包钢梁底板屈服前以荷载增量控制为主,取10 kN为1级进行加载;底板屈服以后改用荷载与位移增量双控的加载方式,取5 kN为1级或多于前一级跨中位移5 mm的级差进行加载。试验全程监测钢梁和混凝土的应变变化,利用量程合适的电子位移计测量组合梁的挠度变形和相对滑移量。试验过程中所有数据均由TDS303数据采集仪自动采集完成,组合梁测点布置如图4所示。

图2 扁豆形花纹钢板

图3 试验装置图

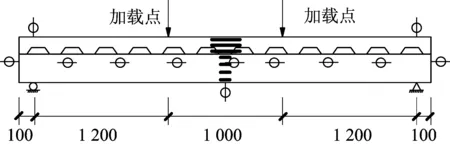
图4 测点布置图

2 主要试验结果

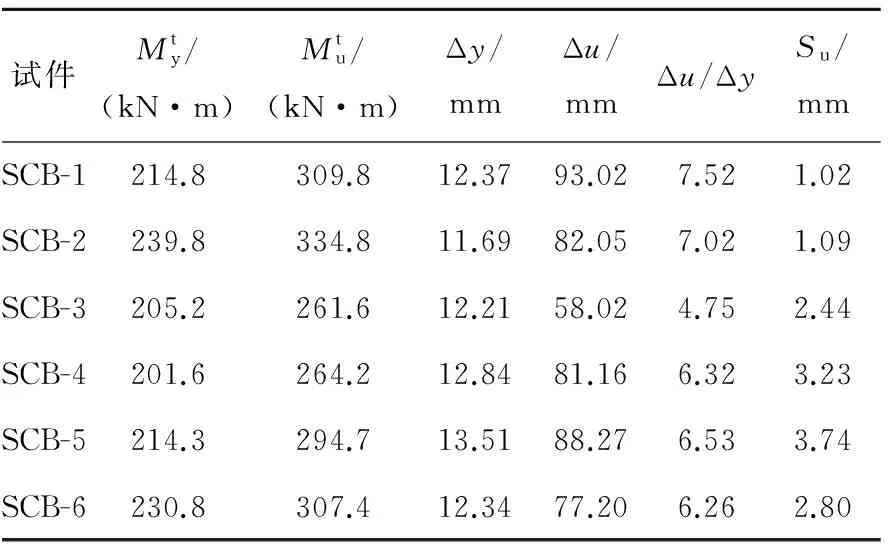
表3 试验结果

图5 组合梁的破坏形式

纯弯段应变沿截面高度的分布情况如图6所示,滑移沿梁长的分布情况如图7所示,挠度沿梁长的分布情况如图8所示。

图6 跨中应变沿截面高度分布

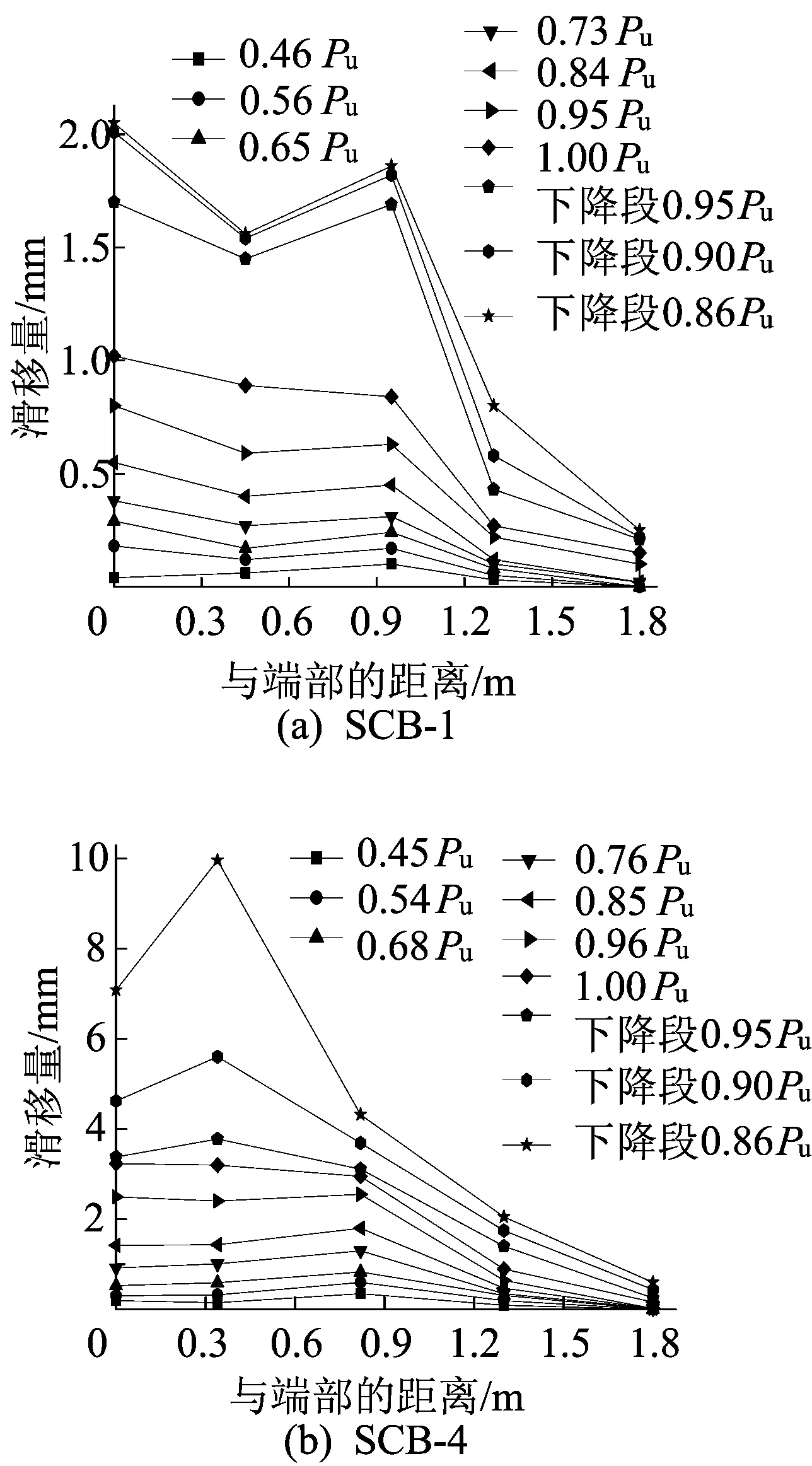
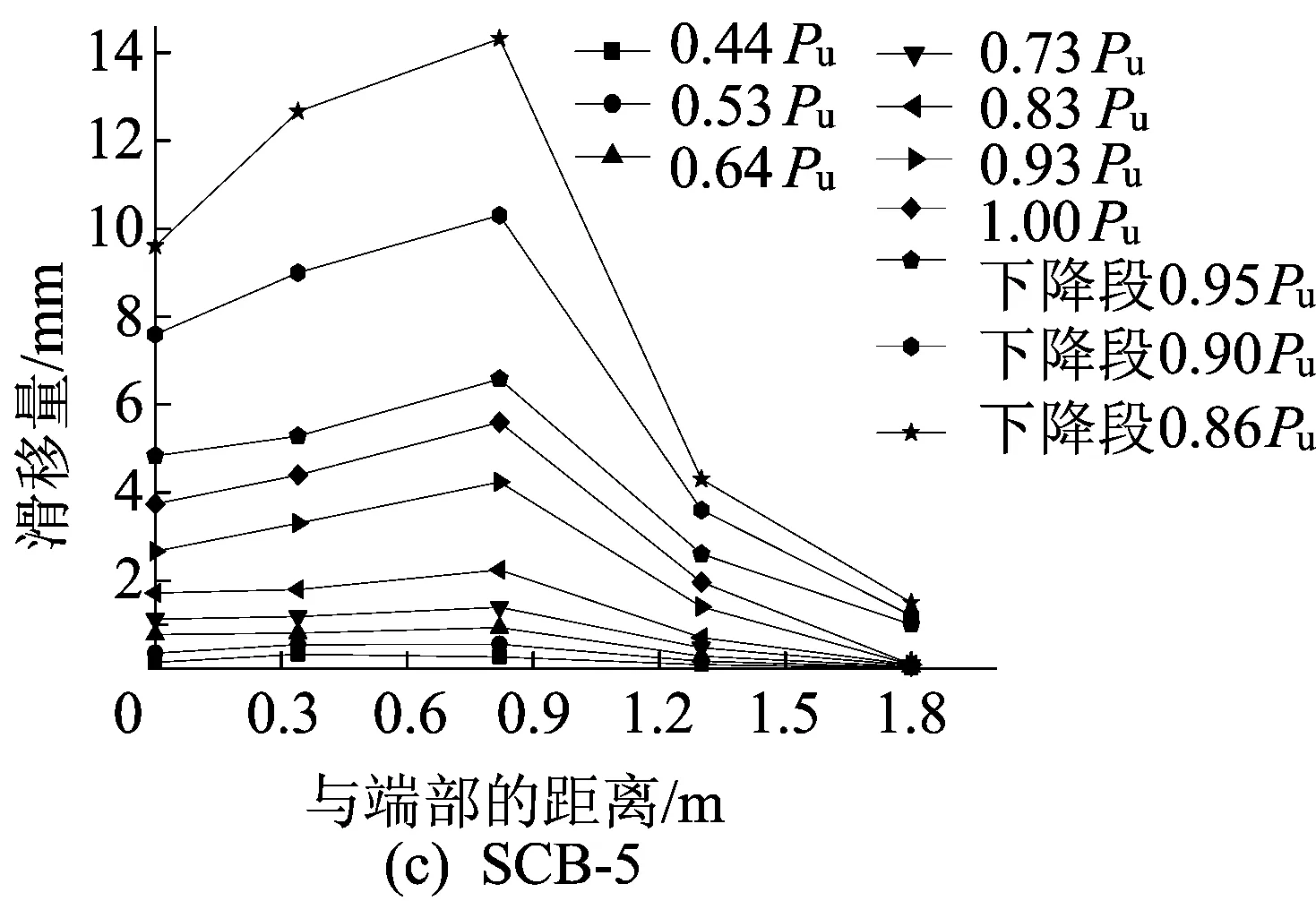
图7 滑移沿跨长分布曲线

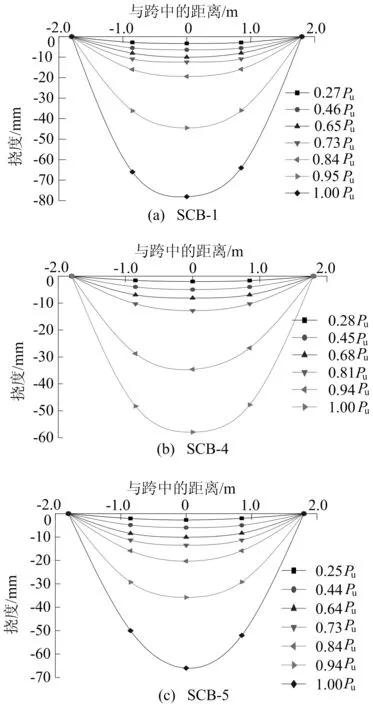
图8 挠度沿跨长分布曲线

从图6～图8可以看出,当荷载水平较低时,抗滑移连接度对组合梁的变形影响较小,各试件挠度和滑移变形基本一致,沿梁的截面高度方向上,应变呈线性分布,符合平截面假定;随着荷载的增加,钢梁和混凝土的应变基本呈线性增大的趋势,跨中挠度也近似呈线性增长,交界面滑移发展速度与抗滑移连接度基本负相关,抗滑移连接度越低的组合梁滑移发展速度越快;继续加载至钢梁底板屈服(约0.75Pu,底板应变16×10-4左右),组合梁截面中和轴开始上移,钢梁和混凝土的应变发展速度加快,不同抗滑移连接度的组合梁滑移变形量差异不断加大,底板屈服时部分抗滑移连接组合梁的端部滑移量约为完全抗滑移连接组合梁的2～3倍,随着钢梁底板的屈服,组合梁的刚度不断降低,跨中挠度呈非线性的加速增长;至极限荷载时,抗滑移连接度对组合梁变形的影响开始宏观地显现出来,部分抗滑移连接组合梁SCB-3～SCB-6端部有明显的滑移现象,而完全抗滑移连接组合梁呈现受弯破坏的特征,混凝土翼板表面有明显的起皮压碎现象,从图6可以得出,随着抗滑移连接度的提高,试件的受弯承载力随之提高且整个截面应变发展更充分,对比极限荷载时各组合梁的挠度沿梁长的分布曲线可知,虽然抗滑移连接度越低的组合梁引起的附加挠度变形越大[1],但抗滑移连接度更高的试件延性更好,挠度发展更为充分;继续加载,试件SCB-1、SCB-2交界面的滑移经过一定发展后趋于稳定,最后混凝土翼板压碎,荷载下降至0.85Pu,宣布试件破坏,试件SCB-3～SCB-6交界面的滑移变形则加速发展,荷载不断下降,降至0.85Pu时停止加载,此时端部混凝土明显滑出钢梁,端部最大滑移量达9 mm。

3 组合梁弹性受弯承载力

3.1 换算截面法计算

钢-混凝土组合梁的弹性受弯承载力[2-3]可以采用换算截面法进行计算,计算模型如图9所示,计算假定如下:

(1) 钢和混凝土均为理想的线弹性体。

(2) 忽略钢梁与混凝土交界面的滑移影响,截面变形符合平截面假定。

(3) 不考虑钢梁腹板内部受拉区混凝土对组合梁弹性刚度的贡献[4-5]。

(4) 不考虑压型钢板肋高范围内混凝土对组合梁惯性矩的影响。

图9 换算截面法计算模型

组合梁换算为等价的钢梁截面面积为:

(1)

换算截面的形心位置距钢梁底板的高度为:

(2)

换算截面的惯性矩为:

(3)

弹性受弯承载力为:

(4)

其中

3.2 滑移效应下的弹性受弯承载力计算

在组合梁弹性受弯过程中,外包钢梁与混凝土之间的C形交界面上存在一定的相对滑移,滑移效应的存在使截面的实际弹性受弯承载力小于上述换算截面法求得的受弯承载力。为定量分析滑移效应对外包花纹钢-混凝土组合梁弹性承载力的影响,将3.1中的假定(2)改为:考虑钢梁与混凝土交界面的滑移影响,且截面C形交界面上的相对滑移相等,由滑移效应引起的附加应力按线性分布;其余假定仍然采用。计算模型如图10所示。

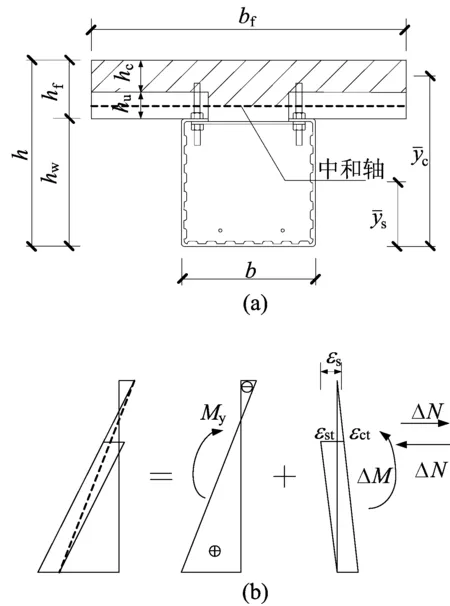
图10 ΔM计算模型

为得到组合梁跨中交界面处的滑移应变,引入外包C型花纹钢-混凝土组合梁在2点对称加载作用下纯弯段的滑移方程[6]:

(5)

(6)

(7)

其中

α、β、γ为计算参数;hf为组合梁翼板的厚度;Ic、Is分别为混凝土梁和外包钢梁的截面惯性矩;yc、ys分别为混凝土截面形心和外包钢梁截面形心到各自上翼缘的距离;τ为外包花纹钢与混凝土之间的黏结力[7-9];U为外包C型钢梁截面周长；l为2个加载点之间的距离；L为梁长。

将纯弯段的滑移S对x求导,可求得滑移应变εs为:

(8)

跨中交界面处滑移应变为:

(9)

根据图10可得:

(10)

(11)

根据(10)式、(11)式求得εst:

(12)

钢梁截面的附加应力合力ΔN为:

(13)

(14)

(15)

其中,hw为花纹钢板腹板高度;hu为压型钢板肋高;hc为压型钢板肋部上方的混凝土高度;Aw为花纹钢梁腹板面积;At为花纹钢梁上翻翼缘面积;as为梁内混凝土纵筋保护层厚度;My为换算截面法所求的弹性承载力。

4 结果分析

采用上述计算公式对组合梁SCB-1～SCB-6的弹性承载力进行计算,并与试验结果进行对比,见表4所列。

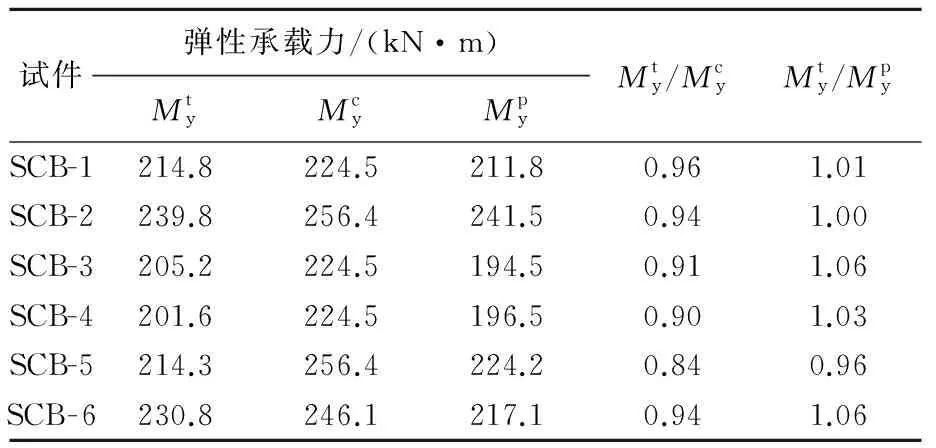
表4 理论计算值与试验值对比

5 结 论

(1) 本试验的外包花纹钢-混凝土组合梁有2种破坏形式,即正截面受弯破坏和整体滑移破坏;抗滑移连接度对组合梁的受力性能影响较大,随着抗滑移连接度的降低,试件的抗弯承载力和延性均随之降低。

(2) 完全抗滑移连接组合梁与部分抗滑移连接组合梁的滑移发展规律在弹性阶段相似,至破坏阶段时,完全抗滑移连接组合梁的滑移趋于停滞,而部分抗滑移连接组合梁则加速发展。

(3) 采用换算截面法计算的组合梁弹性受弯承载力与试验结果误差较大,且计算结果偏于不安全,即使是完全抗滑移连接组合梁,滑移效应引起的附加弯矩仍然不能忽略;考虑滑移效应影响后,弹性受弯承载力计算值与试验结果吻合较好,且计算结果偏于安全,采用滑移修正后的弹性承载力更适用于工程实际。

[1] 聂建国,沈聚敏,余志武.考虑滑移效应的钢-混凝土组合梁变形计算的折减刚度法[J].土木工程学报,1995,28(6):11-17.

[2] 聂建国.钢-混凝土组合结构[M].北京:中国建筑工业出版社,2005:1-3.

[3] 王连广.钢与混凝土组合结构理论与计算[M].北京:科学出版社,2005:1-3.

[4] 宗周红,魏潮文，程浩德，等.帽型截面钢-混凝土组合梁的试验研究[J].建筑结构,2003,33(7):29-33.

[5] 林于东,宗周红.帽型截面钢-混凝土组合梁受弯强度[J].工业建筑,2002,32(9):11-13，59.

[6] 胡红兵.花纹钢板与混凝土之间黏结滑移性能的试验研究[D].合肥:合肥工业大学,2014.

[7] 陈丽华,戴吉祥,金奇亮,等.花纹钢管混凝土黏结滑移本构关系试验研究[J].合肥工业大学学报(自然科学版),2015,38(8):1091-1096.

[8] 陈丽华,戴吉祥,金奇亮,等.花纹方钢管与混凝土间黏结强度的推出试验研究[J].建筑结构,2015,45(3):17-20,26.

[9] CHEN Lihua,DAI Jixiang,JIN Qiliang,et al.Refining bond-slip constitutive relationship between checkered steel tube and concrete[J].Construction and Building Materials,2015,79:153-164.

(责任编辑 张淑艳)

Elastic flexural performance of pattern steel encased concrete composite beam

CHEN Lihua, CHEN Leifei, QU Chuang, XU Ru’nan

(School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

A type of pattern steel encased concrete composite beam with profiled steel sheet was proposed, and in order to study its elastic flexural performance under the influence of slip, the static load test of six full size steel encased concrete composite beams was carried out. The load-slip curves and the load-deflection curves of the specimens were analyzed, and the development law of deformation for composite beams with different degree of shear connection was investigated. Relevant calculation methods of elastic bearing capacity were established according to whether consideration was given to slip effect or not. The test results showed that with the decrease of the shear connection degree, the flexural bearing capacity and ductility of specimens also decreased. When the slip effect was ignored, the average of the ratio of test value to the theoretical value was 0.92 which had large error and the calculation results were unsafe. And when the slip effect was taken into consideration, the average of the ratio of test value to the theoretical value was 1.02, the calculation results were safe and in good agreement with the test results.

pattern steel encased concrete composite beam with profiled steel sheet; elastic bearing capacity; slip; theoretical calculation

2015-07-28；

2015-09-25

安徽省自然科学基金资助项目(1608085ME114)

陈丽华(1972-),女,安徽亳州人,博士,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2016.11.018

TU398.9

A

1003-5060(2016)11-1525-06