地震作用下高土石坝的弹塑性分析

朱亚林, 马 驰, 李端洲, 彭雪峰

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)



地震作用下高土石坝的弹塑性分析

朱亚林, 马 驰, 李端洲, 彭雪峰

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

文章利用快速拉格朗日分析(fast Lagrangian analysis of continua,FLAC)商用软件,应用动力弹塑性分析方法对高土石坝进行大变形分析,讨论了地震作用下坝顶的塑性剪应变的变化过程、坝坡的位移时程变化、坝体永久位移变化,研究了地震作用下高土石坝的破坏性态,为大坝的抗震安全措施提供理论依据。

高土石坝;永久变形;弹塑性

我国西部地区一般位于高烈度地震活动范围内,河谷条件、地质条件和环境条件极度复杂,并且地震强度和发震频率都很高,因此,在西部地区修建大坝水库工程,大坝的抗震安全问题是不容忽视的,特别是对于高土石坝工程,抗震安全问题应作为大坝工程的重点技术问题进行深入研究,并给予稳妥的解决[1-4]。

近年来,有限元、边界元以及离散元等各种数值方法在岩土工程中都有了较大的发展和广泛的应用,然而,这些数值分析方法在理论和采用的算法上都有着各自的局限性。而近年发展起来的快速拉格朗日分析(fast Lagrangian analysis of continua,FLAC),则是在吸收上述方法的优点和克服其缺点的基础上形成的一种新型数值方法。FLAC在动力计算中采用完全非线性弹塑性分析方法,可以遵循任意指定的非线性本构模型,还可以直接计算永久变形,并通过采用合理的塑性方程,使得塑性应变增量与应力相联系[5-6]。

本文利用FLAC商用软件,应用动力弹塑性分析方法,对地震时高土石坝的反应特性进行了系统研究,着重讨论了地震时坝顶的塑性应变变化过程、坝体的永久变形以及坝体网格变形情况,以此研究地震时高土石坝的破坏机理和破坏性态,从而能更好对地震作用下高土石坝的抗震安全进行评价,为合理的抗震措施提供理论依据。

1 计算方法和计算参数

Mohr-Coulomb(M-C)弹塑性模型是描述剪切破坏类材料力学行为的经典模型,该模型具有参数少、工程实例多等特点,FLAC商用软件算例中采用这一模型进行土石坝动力分析,得到了很好的结果。本文计算采用M-C弹塑性模型,对分析过程中材料剪切模量的变化做2点考虑:① 初始剪切模量随围压变化；② 每一计算时间步,对M-C模型的切线模量按照等效线性化模型的思路进行调整,即由当前时间步的剪应变参照模量衰减曲线得到模量衰减因子,用模量衰减因子乘以当前时间步的切线模量[7-8]。对于材料剪切模量的变化，在FLAC程序中通过加入FISH语句来实现,计算结果如图1所示(单位为Pa)。

(1) 剪切弹性模量。

其中,G、σ0′、pa采用同一量纲;pa为大气压,σ0′为平均应力;C为系数；n为指数,其值可由试验结果确定。

图1 坝体初始剪切模量分布

(2) 坝体参数。堆石体的部分计算参数见表1所列[9]。

表1 堆石体的部分计算参数

计算采用上、下游完全对称的心墙堆石坝,坝高为200 m,坝坡为1∶2.0,坝底长为816 m,坝顶长度方向取单位宽度计算。采用位移边界约束条件,模型底面约束竖向位移,侧面均被约束。上游堆石体静力计算时采用浮容重,动力计算时采用饱和容重,水压力直接作用于心墙上游面。大坝体积弹性模量K=13G/6,拉伸强度σt为0。

(3) 输入地震动。模型计算选用的地震波以人工地震波为主,采用拟合糯扎渡坝址区100 a超越概率为2%的人造波,地震峰值加速度为2.83 m/s2,如图2所示。当考虑竖向地震时,竖向加速度峰值取水平向的1/3计算。

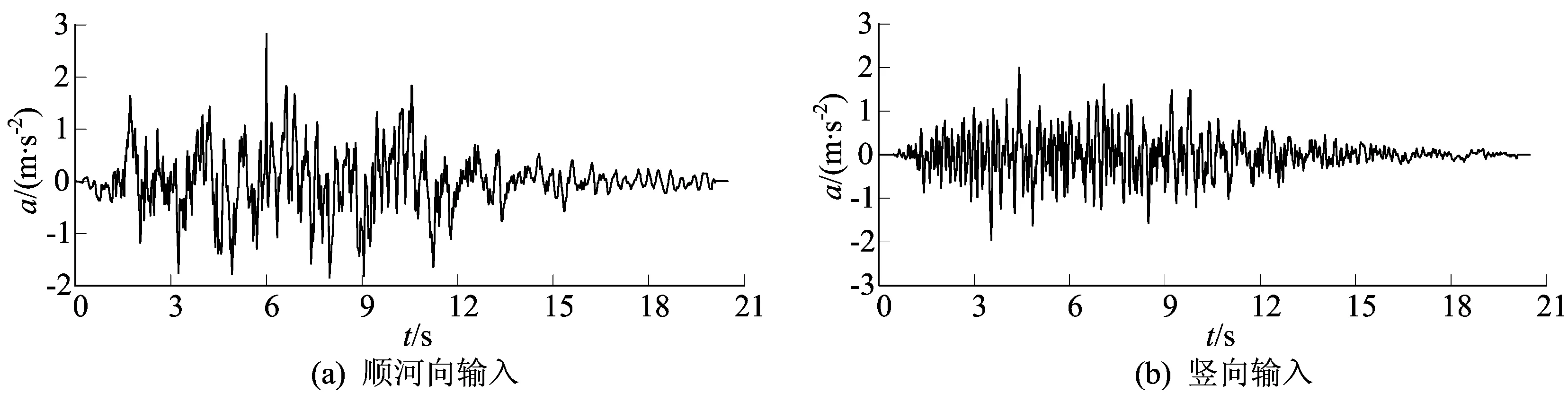
图2 场地反应谱人工波

2 动力反应特性分析

2.1 坝顶部单元塑性区的变化

以往数据表明,地震作用下,虽然高土石坝的宏观破坏性态主要表现为坝顶上部1/5范围内沿坝坡浅层的滑落和坍塌,其位置主要靠近坝顶区附近,发生破坏的原因主要是由于坝体内部累积了较大的塑性变形引起的,因此有必要分析坝体局部塑性区的分布规律。

不同时刻坝顶部单元的塑性区(H=150～200 m)如图3所示。

t=4 s时,坝体的心墙部位和上游部分单元发生剪破坏,拉破坏发生在上、下游面板与坝坡的接触处;t=8 s时,发生剪破坏的单元增多,转移到坝顶和坝体的上、下游,面板发生拉破坏的数量也增加;t=12 s时,坝体单元的剪破坏向坡角延伸,护面板发生拉破坏;t=20 s时,坝体顶部几乎已全部发生了剪破坏,随着剪切破坏的加深,坝体顶部可能已发生整体失稳破坏;随着地震动的结束,t=23 s时,坝体顶部已全部发生剪切破坏。由此可知,地震作用下坝体的破坏主要是由剪切变形引起的,证实了以往的振动台试验结果[10]。

图3 不同时刻坝体顶部单元塑性区(H=150～200 m)

2.2 坝坡的位移时程分析

如果坝坡发生破坏,滑体部分相对于不滑部位将产生较大的相对位移,现选取坝顶与下游坝坡交点作为关键点,其相对于对应的底点的位移-时间曲线如图4所示。从图4可以看出,不论是水平向还是竖向位移均随时间递增,t=6 s时,地震波加速度达到峰值,水平和竖向位移仅分别为0.46 m和0.31 m,此时坝坡并没有破坏。因此地震波峰值达到最大值不一定是坝坡动力破坏的时刻,这点与以前的研究成果是一致的[10]。到t=16 s左右时,位移达到最大值,潜在滑体产生较大的滑动,但没有剧烈的突变,直到t=23 s后出现不变的位移,但是坝坡的整体稳定性还需进一步分析。

图4 坝坡相对位移-时间曲线

不同时刻的坝坡水平位移等值线图如图5所示(单位为m)。

从图5可以进一步更明显地看出坝坡的位移变化趋势,下游坝坡的水平位移较大,当t=12 s时,坝坡的位移变化趋势很明显,直到地震结束,坝坡水平位移等值线图没有太大变化。随着地震的持续作用,剪切破坏逐渐由坝顶向下游伸展,随着破坏深度逐渐增加,剪切滑移带形成贯通的破裂面,并且可以观察到地震作用下坝坡破坏是一个过程,而不是在某一时刻完成。

图5 不同时刻坝坡的水平位移等值线图

2.3 坝体的永久位移变化

坝体特定位置的水平和竖向永久位移能够在一定程度上反映坝体最终的变形,可用来判断边坡的稳定状态,坝体内永久变形积累到一定程度就会发生失稳破坏。因此,高土石坝动力反应计算时应重视对永久变形的分析,特别是对靠近坝顶局部区域的地震永久变形分析。

2.3.1 坝体中各特征点的位移时程曲线

坝体中各特征点的位置示意图如图6所示,编号中的数字同时是特征点所处的位置标高,底面标高为0。心墙各特征点的水平和竖向位移时程变化曲线如图7所示，下游坝坡各特征点的水平和竖向位移时程变化曲线如图8所示。

从图7可以发现各点的位移随时间的变化趋势相似,离坝顶较近的2点X200和X184变化较明显,位移较大;X160和X136在坝高1/5以下,位移变化较小,即地震作用下坝体上部的位移变化较大;在0～2 s阶段位移几乎不变化,在2～12 s阶段位移增长较快,地震的峰值出现在6 s时刻,后期增长缓慢,到地震结束时位移几乎保持稳定趋势,坝坡可能已失稳破坏;标高越高位移越大,心墙顶点的水平和竖向位移最大,最大值分别为0.64、0.83 m。从图8可以发现各点位移随时间变化趋势相似,下游坝坡水平位移最大值不是发生在坝顶,而是在坝顶1/5范围内,这主要和坝顶的宽度有关,竖向位移最大值发生在坝顶。

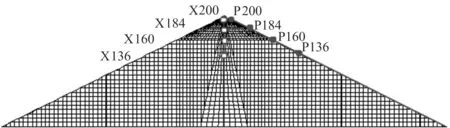
图6 心墙与坝坡各特征点的位置示意图

图7 心墙各特征点的位移时程变化曲线

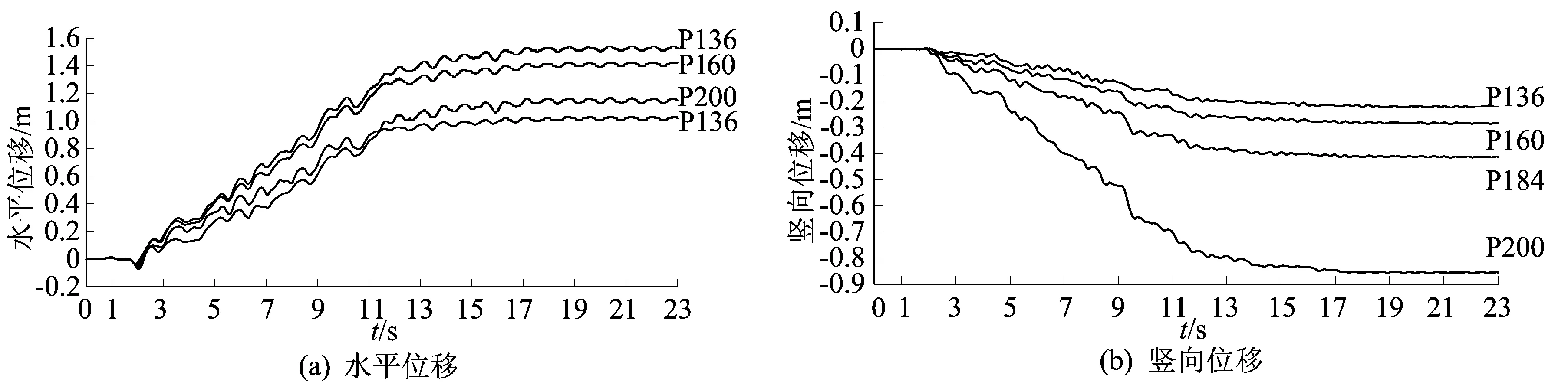
图8 下游坝坡各特征点的位移时程变化曲线

2.3.2 不同地震输入方式下坝体永久位移变化

坝体下游的永久位移随坝高的变化如图9所示,考虑单向输入和双向输入。

从图9可以看出:① 坝体下游的水平永久位移曲线沿坝高方向规律分布,坝体上部1/5范围内,水平永久位移变化较明显,最大值发生在坝体上部,大小为1.56 m;②坝体下游的竖向永久位移曲线沿高度逐渐递增,坝体上部1/5范围竖向永久位移变化较大,最大值发生在坝坡顶部,大小为0.86 m;③考虑竖向地震动输入时,永久位移的变化规律相似,永久位移值增加到1.76、0.99 m,增幅分别为12.8%和15.1%,因此对于高土石坝的坝坡稳定分析,不能忽略竖向地震动的影响;④ 强震作用下,坝体上部1/5范围位移变化较大,坝体的最大水平和竖向永久位移均发生在坝顶及附近,所以应加强坝顶区堆石体的稳定,特别是下游坝坡的变形较明显,可适当减缓下游坝坡坡度。

图9 下游沿坝高方向的水平和竖向永久位移变化

3 结 论

(1) 强震作用下,大坝的剪应变在坝顶处及坝坡上部较大,最大剪应变发生在坝顶处。地震作用下坝体的破坏主要是由剪切变形引起的,地震结束时坝体顶部已几乎全部发生剪切破坏。

(2) 下游坝坡各特征点的水平和竖向位移时程变化趋势相似,下游坝坡的水平位移最大值不是发生在坝顶,而是在坝顶1/5范围内,这主要和坝顶的宽度有关,竖向位移最大值发生在坝顶。

(3) 同时考虑竖向地震动作用时,下游坝坡的永久变形变大,在坝坡稳定分析时不可忽略竖向地震动的影响。

[1] 贾金生,袁玉兰,李铁洁.2003年中国及世界大坝情况[J].中国水利,2004(13):25-33.

[2] 赵剑明,常亚屏,陈宁.加强高土石坝抗震研究的现实意义及工作展望[J].世界地震工程, 2004,20(1):95-99.

[3] 祁庆和.水工建筑物[M].3版.北京:中国水利水电出版社,1997:1-100.

[4] 倪汉根,金崇磐.大坝抗震特性与抗震计算[M].大连:大连理工大学出版社,1994:1-50.

[5] 彭文斌.FLAC3D实用教程[M].北京:机械工业出版社,2008:1-60.

[6] 陈育民,徐鼎平.FLAC/FLAC3D基础与工程实例[M].北京:中国水利水电出版社,2009:210-240.

[7] Itasca Consulting Group,Inc.Fast Lagrangian analysis of continua in 2 dimensions, version 4.0,user manual[Z]. Itasca Consulting Group,Inc,2002.

[8] 黄润秋,许强.显示拉格朗日差分分析在岩石边坡工程中的应用[J].岩石力学与工程学报,1995,14(4):346-354.

[9] 朱亚林,朱大勇,王思雁,等.土工格栅加筋坝坡的抗震效果研究[J].合肥工业大学学报(自然科学版),2011,34(10):1518-1523.

[10] 李永胜.边坡振动台模型试验及相关问题研究[D].大连:大连理工大学,2009.

(责任编辑 张淑艳)

Elasto-plastic analysis of high earth-rockfill dam under earthquake

ZHU Yalin, MA Chi, LI Duanzhou, PENG Xuefeng

(School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

The large deformation analysis of high earth-rockfill dam subjected to earthquake is presented by using the dynamic elasto-plastic analysis method with fast Lagrangian analysis of continua(FLAC) commercial software. The change of plastic shear strain of dam crest, the time-history change of the displacement of dam slope and the change of permanent displacement of dam body during earthquake are researched. And the damage properties of high earth-rockfill dam under earthquake are studied. The conclusion can provide a theoretical basis for the choice of the corresponding anti-seismic measures.

high earth-rockfill dam； permanent deformation； elasto-plastic

2016-04-07；

2016-10-10

国家自然科学基金资助项目(51409076);安徽省自然科学基金资助项目(1408085QE89)

朱亚林(1979-),女,安徽庐江人,博士,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2016.11.017

TV641.1

A

1003-5060(2016)11-1520-05