激光熔覆成形尖角插补算法优化与实现

刘家俊, 黄 英, 袁自钧, 陈向东, 高 峰

(合肥工业大学 电子科学与应用物理学院,安徽 合肥 230009)



激光熔覆成形尖角插补算法优化与实现

刘家俊, 黄 英, 袁自钧, 陈向东, 高 峰

(合肥工业大学 电子科学与应用物理学院,安徽 合肥 230009)

文章通过对激光熔覆过程中机器人在尖角处过渡时产生的误差进行分析,提出了机器人在尖角处匀速过渡的插补算法。通过在尖角外围添加补偿点并精确控制激光开/关设计了机器人插补流程,利用C#.NET编程语言编写机器人插补软件,并采用OpenTK实现插补运算后的数据可视化。仿真和实验验证机器人路径的可行性,并成功熔覆出含有60°尖角的薄壁件。研究结果为激光熔覆含有尖角特征的薄壁件提供了理论指导和实验依据。

激光熔覆;机器人;尖角薄壁件;插补算法;轨迹规划

0 引 言

激光熔覆成形技术是激光直接制造金属零件技术的一种,又称为激光近净成形(laser engineering net shaping,LENS)技术[1-3],多用于高价值大型复杂金属零件的制造[4-5]、修复[6-7]及表面改性等[8-9]。激光熔覆成形薄壁类零件已经得到了广泛关注与研究[10-11]。然而,对于带尖角薄壁件的研究较少,且利用激光熔覆成形技术在制造薄壁件时存在不同类型的难题有待解决。

激光熔覆成形在堆积直线段或圆弧段类型的薄壁件相对简单,这缘于激光沿直线扫描时速度和方向都可保持不变,沿圆弧扫描时速度大小不变,仅方向沿着圆弧的切线方向逐步圆滑变化,因此,这2种类型薄壁件成形相对容易控制与成形。相比之下,含有尖角特征的薄壁件在激光熔覆成形时较难。

因为含有尖角特征的薄壁件经过软件分层处理后,截面信息中至少存在2个图元以非相切的形式相接,例如直线段与直线段的相接、直线段与圆弧段以非相切形式的相接等，所以与直线段或圆弧成形相比,其主要表现为尖角处扫描速度的突变,即扫描速度大小呈先减小后增加的趋势,方向改变等。扫描速度的变化会导致尖角过渡区域因相对熔覆时间较长产生凸起,很大程度上影响成形件的成形质量,甚至于导致成形失败。

为克服上述问题,本文分析了在尖角处产生误差的原因,并设计了插补算法和机器人路径插补软件,有效地提高了含尖角特征的薄壁件的成形效果。

1 误差分析

成形系统通常由六轴机器人、同轴送粉熔覆头、激光器和冷却机等构成。激光熔覆制造原理是基于三维建模软件生成零件的计算机辅助设计(computer aided design,CAD)模型,将CAD模型离散为一系列空间坐标点,机器人根据坐标点依次运动,金属粉末在激光的作用下形成熔道,逐层熔覆堆积出所需形状的金属零件。

在激光熔覆成形过程中,送粉率和激光能量密度等参数是决定零件成形质量好坏的关键性因素[12]。通常需要激光功率、送粉率、机器人移动速度等均保持恒定。其中激光功率恒定和送粉率恒定的实现都较为简单,而机器人移动速度则受限于机器人运动特性不易保持恒定。机器人末端激光器在伺服电机带动下由P1点开始加速运动后匀速运动,在抵达P2点前开始减速,直到在P2点速度为0,再开始下一段运动,如图1所示。同理,P2～P3段、P3～P4段都不可避免地要经历一个加速—恒速—减速—停止的过程。

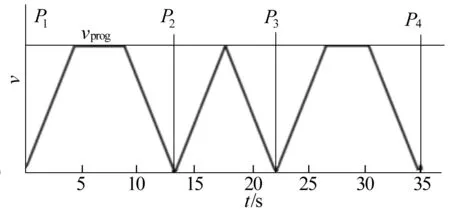
图1 机器人运动特性示意图

正方形薄壁件如图2所示，机器人在各点之间运动速度的变化导致了激光熔覆中能量密度和送粉量的变化,4个直角处因为机器人速度变化而出现了明显的凸起,严重影响了激光熔覆的成形效果。

图2 正方形薄壁件

为克服因机器人运动速度不恒定而引起的成形误差,文献[13]提出了一种采用电荷耦合元件(charge coupled device,CCD)实时监测激光喷头与加工熔池之间的距离,并将检测距离实时反馈至计算机,并与原始设定值进行比较和差值运算。在每步结束后,将差值补偿到下一步中,以完成提升量的补偿。该方法虽然能够减缓在拐角处的凸起,但硬件成本高,且控制过程相对复杂。

在机器人恒速控制领域,插补运算方法常被应用于机器人连续运动中,多采用三次样条曲线或圆弧插补的方法使机器人在拐角处尽量平滑过渡,如图3所示。

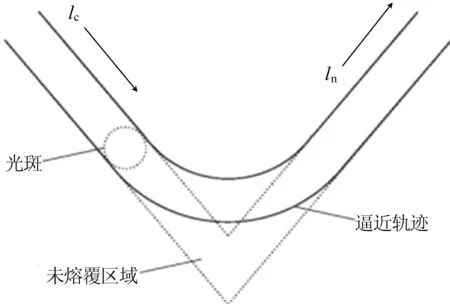
图3 圆弧过渡示意图

图3中,lc为当前熔道;ln为下一个熔道,在机器人接近拐角时会用逼近轨迹代替原来的轨迹。该方法虽然能让机器人在拐角处不会停顿,但由于在拐角内侧插入了过渡曲线,从而导致拐角处产生了较大的未熔覆区域,以致造成较大的成形误差。

2条圆弧相切时的过渡曲线示意图如图4所示。由图4可以看出,若两条圆弧相切,采用上述方法则机器人根本无法到达P2点,产生的轨迹误差则会更大,无法满足制造需求。

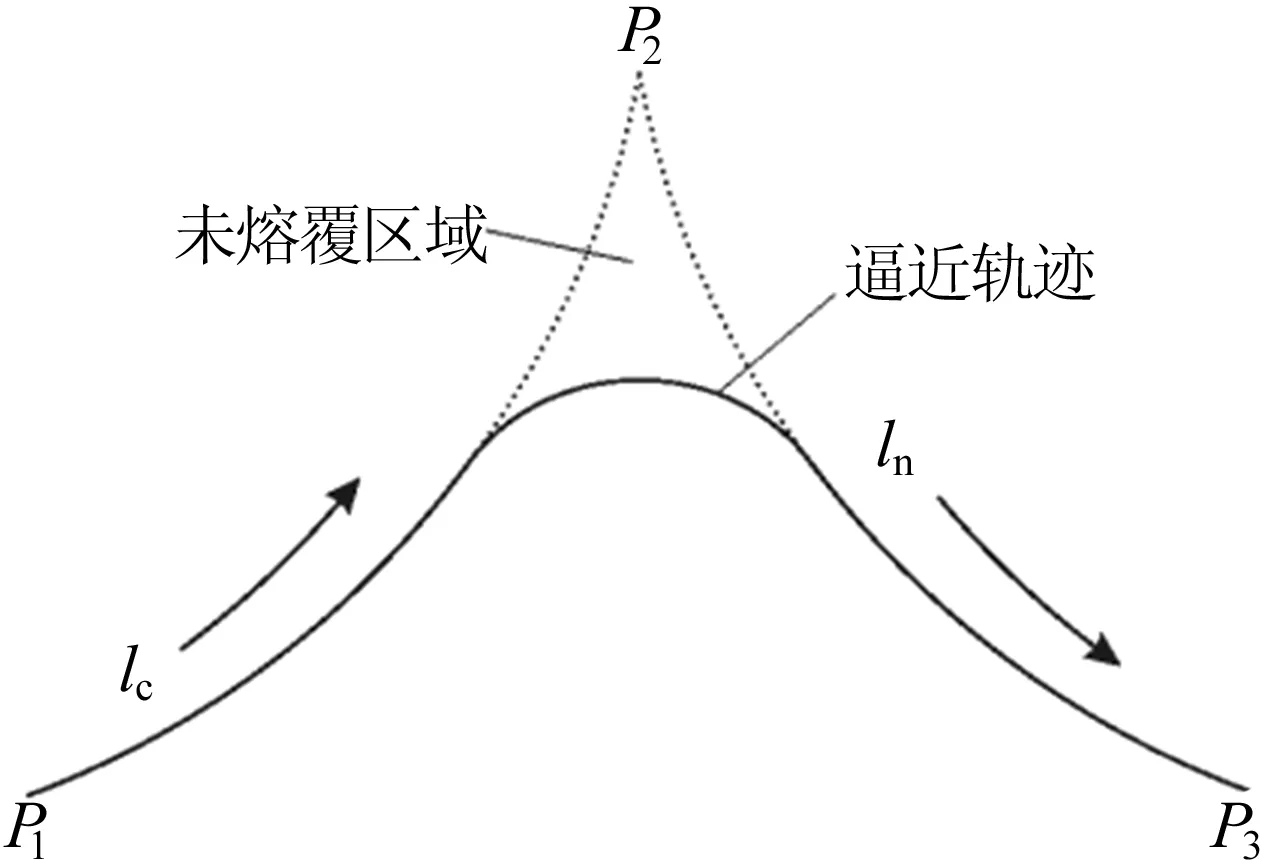
图4 2条圆弧相切时的过渡曲线示意图

2 机器人恒速过渡插补算法

2.1 尖角过渡插补算法

针对上述方法在熔覆成形带尖角薄壁件方面的不足,本文提出一种适用于机器人在尖角处恒速控制的插补算法,其原理是利用尖角外侧额外插入2个点以避免机器在尖角处减速。尖角过渡插补算法示意图如图5所示,图5中,Pn为当前点;Pn-1为前一个点;Pn+1为后一个点;T和S为要插补的2个点。

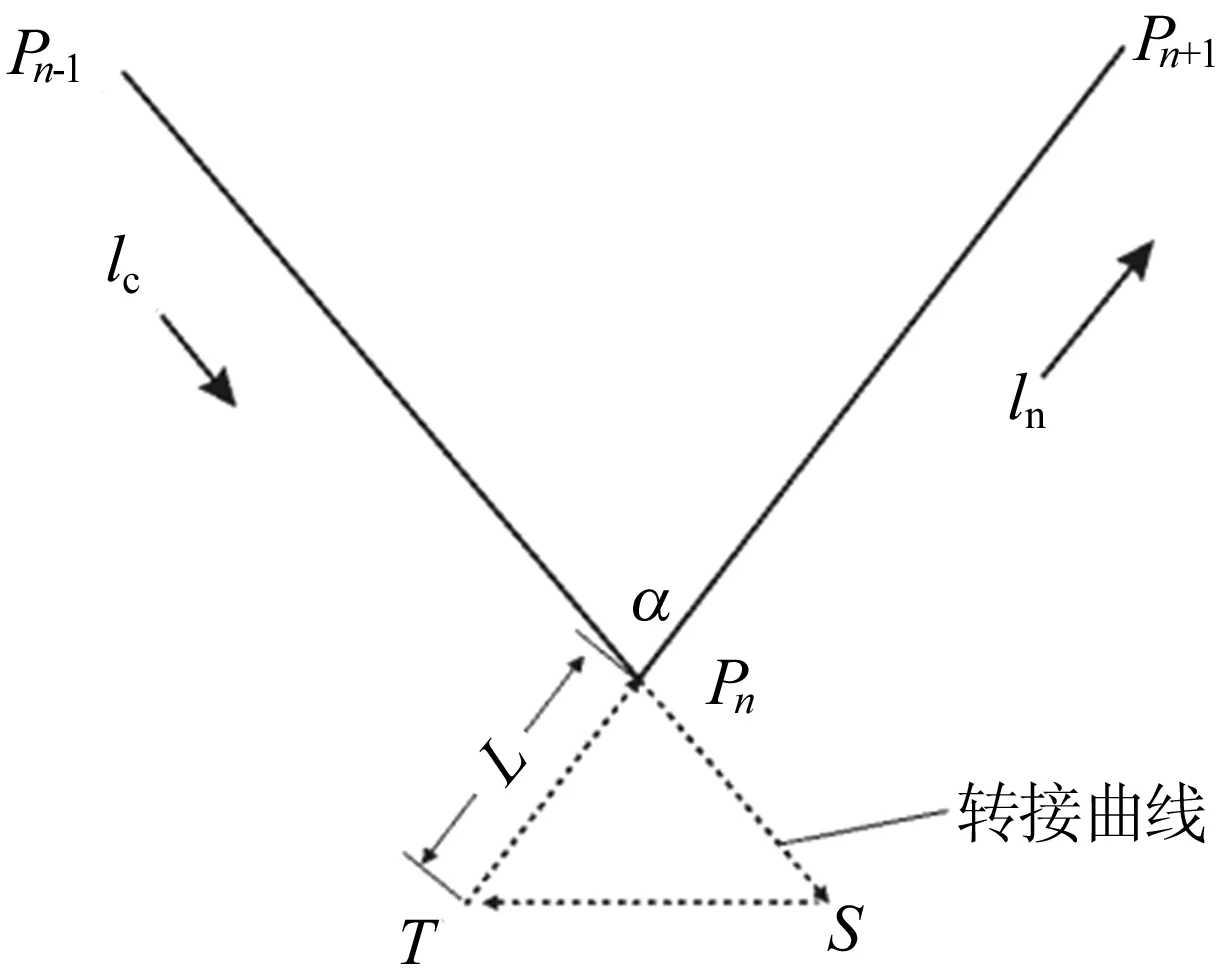
图5 尖角过渡插补算法示意图

机器人实际的运行轨迹是Pn-1—Pn—S—T—Pn—Pn+1,通过精确控制激光器的开关,使第1次到达Pn点时关闭激光,第2次到达Pn点时打开激光,可以保证机器人在经过尖角Pn时速度的大小不发生改变。其中,L的长度应不小于机器人从0加速到匀速的距离。此时,Pn点可以被看作熔覆了2次,多层堆积后依然会产生凸起,为此,改进的方法是通过设置激光器的开/关光延时,来使Pn-1Pn和PnPn+12条直线段较好地搭接在一起。具体算法如下:

计算当前点Pn分别与前一个点Pn-1和下一个点Pn+1所组成向量的夹角的大小α,根据(1)式和(2)式计算夹角大小,并判断是否需要进行插补。(1)式、(2)式具体如下：

(1)

(2)

若需要插补,通过(3)～(6)式计算出点T和点S的坐标，具体如下：

(3)

(4)

(5)

(6)

(7)

其中,Tx、Ty、Sx、Sy分别代表点T和点S的x轴坐标和y轴坐标；Pnx、Pny、Pn-1x、Pn-1y、Pn+1x、Pn+1y分别代表Pn、Pn-1和Pn+1的x轴坐标和y轴坐标。L需满足(7)式,其中a为机器人的加速度,V为机器人设定的工作速度。L的值需根据制造零件的大小及工作台的范围进行设定。

2.2 不同角度的过渡

上述算法提供了一种机器人拐角过渡的设计方案,能保证在需要熔覆成形的每一条线段上都保持速度恒定,但由于将熔覆成形的路径拆分成不连续的2段,需要考虑到线段与线段之间的搭接问题。以直角过渡为例,直角过渡示意图如图6所示,lc为当前熔覆段,ln为下一个熔覆段,当机器人抵达E点后关闭激光器,再经过插补点T和S,进入下一个熔覆段ln。此时,选取激光器再次开启的位置十分重要,一般选取在E和F之间。若开光点距离F点较近，则会产生较大的未熔覆区；反之，开光点距离E点较近则会在直角处过度堆积,多层熔覆后会产生凸起。

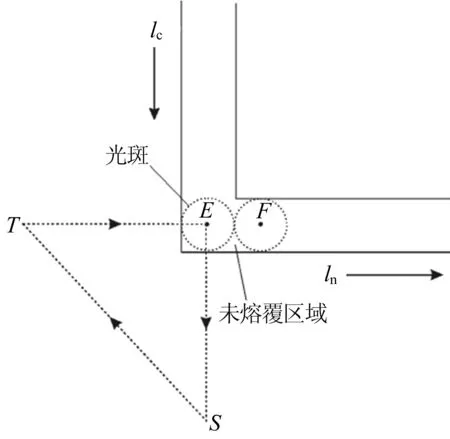
图6 直角过渡示意图

由于直线与直线的搭接受多个变量相互作用,通过理论计算得到最佳开光点较为繁杂,本文通过试验得出在E和F的中点处开激光会使直角处的成形效果较好,不易出现凸起。即在激光器抵达E点后延迟一个光斑半径的距离r后再开光,如图7所示。其中阴影部分为二次熔覆区域,该区域需保证在合适的范围内,以填补熔道边缘的塌头,使2条熔道平整地搭接在一起。若二次熔覆的面积过大，则会堆积过多粉末,产生凸起;反之，若二次熔覆的面积太小，则会在2条熔道搭接处产生缝隙。

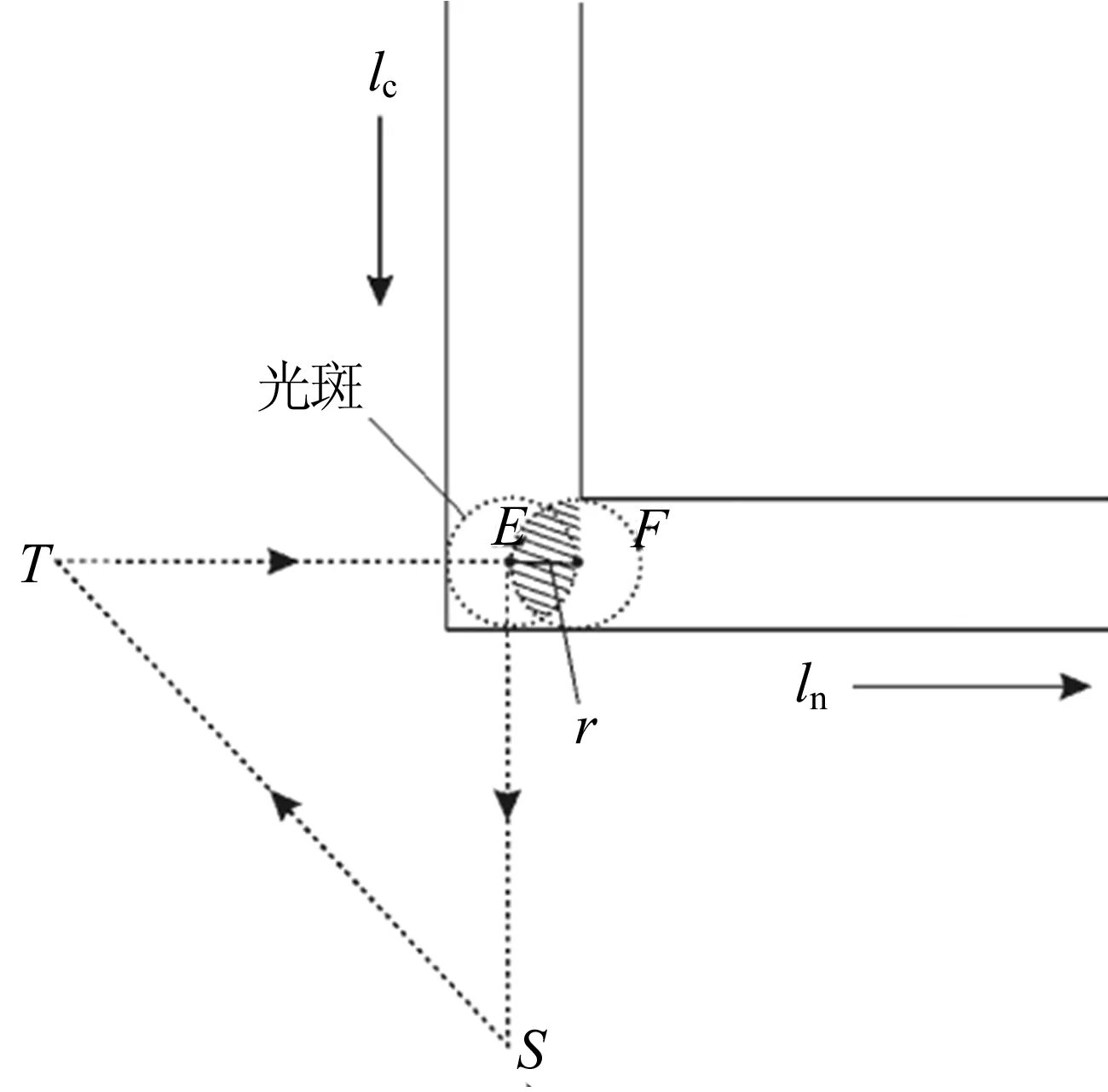
图7 直角过渡中推迟距离r后开光示意图

假设当前熔道与下一个熔道相夹45°时,关光点E和开光点F相距仍为光斑半径,如图8所示,由图8可以明显发现二次熔覆的区域面积变大了,意味着会有更多的粉末被熔覆在了熔道lc上,多次堆积后会产生凸起。由此可知,不同角度间的搭接率并不能简单地设为一个定值,对于不同的角度值的过渡所需要的开光延时是不同的。改进方法是将开光点放置在当前熔道lc的内侧边线上,能有效减小二次熔覆区域的面积并保持在合理的范围之内,如图9所示,则关光点E与开光点F的距离d满足

(8)

其中,r为光斑半径;α为2条熔道所夹角度。

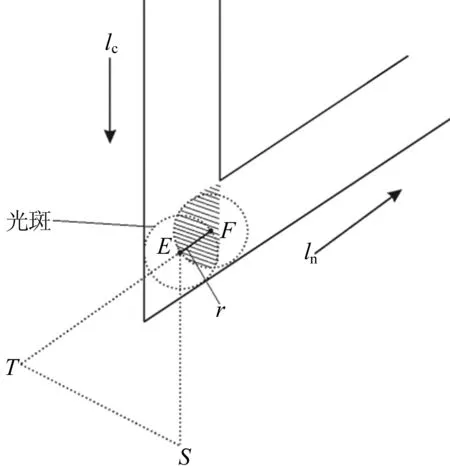
图8 尖角过渡中推迟距离r后开光示意图

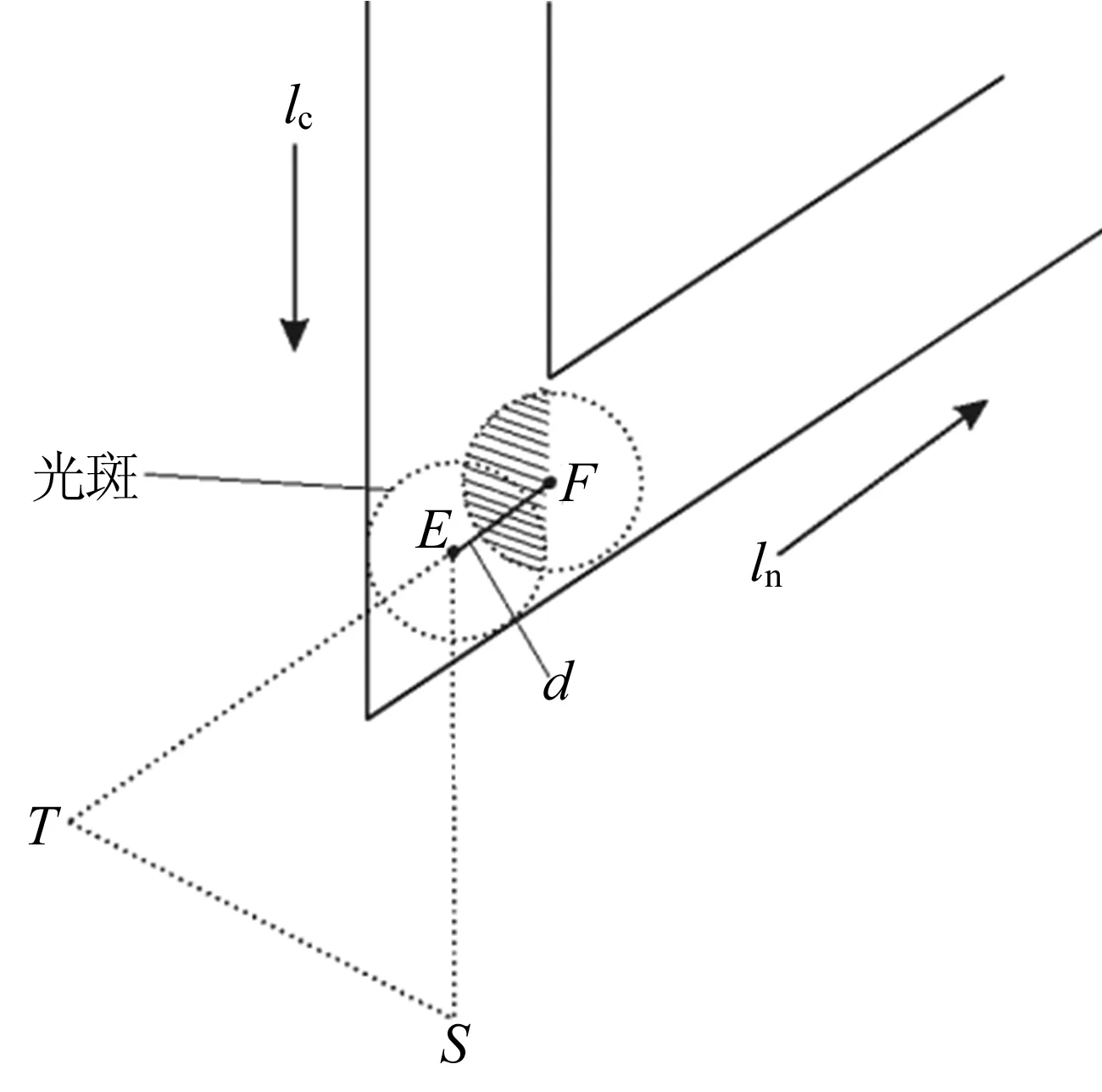
图9 尖角过渡中推迟距离d后开光示意图

3 插补程序设计与实验

3.1 插补程序设计

为能验证并实现上述算法,本文采用C#.NET 编程语言对算法进行编程并编译成机器人插补软件,其流程如图10所示。

程序读取经过三维模型切片处理后的cli文件,将cli文件中的点集存入程序列表中。因为CAD文件经过切片处理后点与点之间的间距很小,数据量较大,所以有必要将点集进行一次粗插补,从而可以减少数据冗余、避免机器人运行过程中发生抖动。将粗插补后的点更新到程序列表中,再计算每个点所在的角度值来判断是否需要插补过渡点并将需要插补的点作特征标记,其特征标记的目的是为了在标记点后加入开/关光命令,之后再次更新程序列表中点集。更新完毕后,将数据转换成KUKA机器人可识别的DAT文件和SRC文件,其中DAT文件和SRC文件分别存储运动数据命令和运动控制命令。

图10 算法程序流程

数据可视化不仅可以方便实验人员观察插补后的路径是否合理,还可以模拟机器人运行轨迹,为实验结果的可行性提供参考,提高实验效率。本文采用免费的数据可视化方案OpenTK,提供了OpenGL的.NET实现。其程序界面及插补前的结果如图11所示，插补后的结果如图12所示。

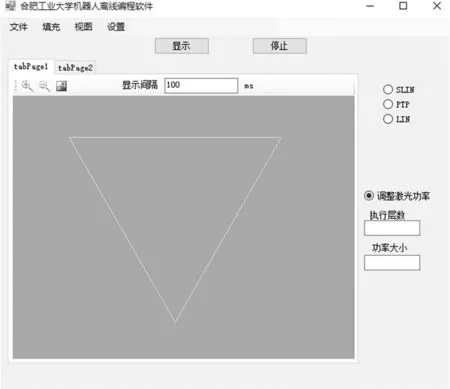
图11 程序界面及插补前的结果

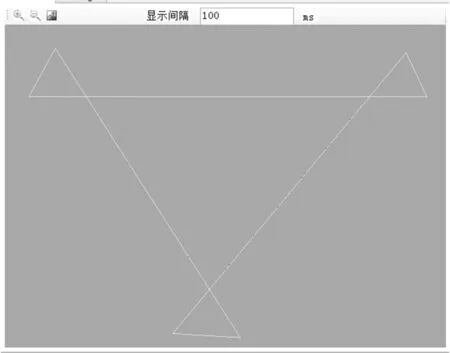
图12 插补后的三角形

由图12可以看出,通过在每个尖角处增加2个插补点,以实现尖角处匀速过渡。

3.2 实验验证

合肥工业大学激光熔覆再制造系统的硬件设备主要由机器人系统、供粉系统、冷却系统、激光系统等部分组成。机器人为KUKA KR 30 HA型六自由度关节型多功能智能机器人;供粉系统为 GTV PF2/2型送粉器,使用氩气作为送粉气和保护气;冷却系统为PH-LW190-TH2P型冷水机;激光器系统为LDF 6000-100 VGP型半导体激光器。

实验用材料为45#钢基板和80目Ni-60合金粉末,实验前先用乙醇擦洗基板表面,再用激光沿着将要行走的路径照射一遍,从而可以预热基板并除去锈迹。激光熔覆成形的工艺参数为:激光功率1 400 W,机器人移动速度3 mm/s,光斑直径4 mm,Z轴抬升量0.3 mm,整个成形过程均在惰性气体氛围下进行,实验模型为带有60°尖角的薄壁件。为了进行对比,未进行优化前的激光熔覆实例如图13所示,熔覆50层后的成形效果如图14所示。

图13 优化前的激光熔覆实例

图14 带有60°尖角的金属薄壁件

通过对比图13、图14可以看出，本文提出的方法可以有效地克服含有尖角特征薄壁激光熔覆过程产生的凸起。

4 结 论

为克服激光熔覆含有尖角特征薄壁零件时在尖角处出现凸起问题,文中提出了一种尖角过渡插补算法。为验证插补算法的有效性及模拟机器人运动轨迹,设计了数据可视化路径规划软件,提升了工作效率。并分析了不同角度下,关光点与开光点之间的距离对熔覆效果的影响,对插补算法进行改进,优化了熔道搭接质量。经60°尖角熔覆实验,在熔覆50层后尖角处仍然没有凸起,2条熔道间没有缝隙或裂痕,实验结果为含有尖角特征的薄壁件激光熔覆提供了理论指导和实验依据。基于本算法开发的应用软件可以实现角度判别、路径插补、工艺参数设置、机器人路径仿真等功能,极大地提高了操作人员的实验效率。

[1] 张冬云,王瑞泽,赵建哲,等.激光直接制造金属零件技术的最新进展[J].中国激光,2010,37(1):18-25.

[2] 宋建丽,李永堂,邓琦林,等.激光熔覆成形技术的研究进展[J].机械工程学报,2010,46 (14):29-39.

[3] ENSZ M,GRIFFITH M,HOFMEISTER W,et al.Investigation of solidification in the laser engineered net shaping (LENS) process:SAND99-1550JON:DE00007871[R].Albuquerque:Sandia National Laboratories (SNL),1999.

[4] QI H,AZER M,SINGH P.Adaptive toolpath deposition method for laser net shape manufacturing and repair of turbine compressor airfoils[J].The International Journal of Advanced Manufacturing Technology,2010,48(1):121-131.

[5] 王华明.航空高性能金属结构件激光快速成形研究进展[J].航空制造技术,2005(12):26-28.

[6] 崔爱永,胡芳友,张忠文,等.钛合金表面激光熔覆修复技术[J].中国表面工程,2011,24(2):61-64.

[7] 杨毅,曾庆生.齿轮失效及激光熔覆修复技术的研究[J].机械工程师,2014(7):14-16.

[8] 韩彬,齐从华,王勇,等.激光熔覆-离子渗硫复合改性层的减摩耐磨性能[J].中国表面工程,2014,27(4):70-75.

[9] 陈长军,张敏,王晓南,等.无限冷硬铸铁轧辊的激光表面改性[J].中国激光,2013,40 (增刊1):96-100.

[10] 刘继常,李力钧.激光熔覆成形金属薄壁结构的试验研究[J].机械工程学报,2005,40(10):185-188.

[11] 王续跃,王彦飞,江豪,等.圆形倾斜薄壁件的激光熔覆成形[J].中国激光,2014,41(1):0103006-1-0103006-6.

[12] 李鹏.基于激光熔覆的三维金属零件激光直接制造技术研究 [D].武汉:华中科技大学,2005.

[13] 何正东.基于机器人激光熔覆尖点过渡薄壁件成形研究[D].苏州:苏州大学,2014.

(责任编辑 闫杏丽)

Optimization and realization of sharp corner interpolation algorithm for laser cladding forming

LIU Jiajun, HUANG Ying, YUAN Zijun, CHEN Xiangdong, GAO Feng

(School of Electronic Science and Applied Physics, Hefei University of Technology, Hefei 230009, China)

The error resulting from robot’s transition at sharp corner during the laser cladding process was analyzed, and an interpolation algorithm with the characteristic of uniform transition at closed angle for laser cladding robot was introduced. The interpolation process was demonstrated by using the methods of adding compensation points at the sharp corner and controlling the laser on/off precisely, and the algorithm software was programmed by C#.NET programming language. To achieve the data visualization, the corresponding display interface in OpenTK was proposed. The simulation and experimental results verified the feasibility of the robot path, and a thin-walled part with a sharp corner of 60° was successfully clad. The study can provide theoretical guidance and experimental basis for laser cladding on thin-walled part with angle characteristic.

laser cladding; robot; thin-walled part with sharp corner; interpolation algorithm; trajectory planning

2015-08-31；

2015-12-02

合肥工业大学产学研校企合作资助项目(13-522)

刘家俊(1990-),男,安徽合肥人,合肥工业大学硕士生; 黄 英(1960-),女,安徽合肥人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2016.11.015

TG665

A

1003-5060(2016)11-1509-06