变焦相机自标定方法研究

赵书俊,段绍丽,张晓芳,李 磊,刘晓旻

(郑州大学 物理工程学院，河南 郑州 450001)



变焦相机自标定方法研究

赵书俊,段绍丽,张晓芳,李 磊,刘晓旻

(郑州大学 物理工程学院，河南 郑州 450001)

研究了变焦式相机的标定方法，采用基于二消失点的自标定方法对变焦摄像机的两个固定焦距下的一般参数进行标定，通过与张正友标定方法、机器视觉软件Halcon标定的结果进行比较，验证了该方法的可行性和鲁棒性.为了能够更好地反映变焦相机的变焦特性，建立了能更精确描述变焦摄像机的厚透镜模型.笔者通过对变焦图像进行SIFT特征匹配，根据匹配点对建立直线方程组，采用最小二乘方法估计变焦图像的缩放中心，另外，还计算了不同焦距之间的光心位移.实验结果表明，光心位移与焦距的变化量有明显的差距，从而说明厚透镜模型更适合用来描述摄像机的变焦镜头.

变焦相机标定；二消失点；亚像素角点检测；缩放中心；光心位移

0 引言

相机标定是从二维图像获取三维空间深度信息的关键步骤[1-2].相机标定方法主要分为标定板标定方法、主动式标定法、相机自标定方法[3].标定板标定法需要精密加工的标定物，利用二维图像与三维场景的匹配对应关系来标定相机参数；主动式标定法不需标定物，算法简单，鲁棒性较高，缺点是需要精确控制相机运动，实验设备要求高[4].自标定方法不需要标定物，仅利用二维图像信息来确定相机内参数[5].

由于变焦镜头比固定焦距镜头具有更大的功能和弹性，变焦镜头的摄像机系统能适应各种视野、景深和光照条件的场景.目前，变焦镜头在深度重建、安全监控、视觉跟踪、精密测量等领域得到了广泛应用和研究. 2013年南开大学张雪波等[6]提出了一种基于多参考点的变焦转换模型标定方法，提高了标定的精度，并将其成功地应用于视频监控系统下人体的身高测量中.石皓[7]提出了一种用于鱼眼PTZ主从监控系统的标定方法.2014年S.lvarez[8]提出一种应用在ITS(智能交通系统)框架中的分层单目摄像机自动标定方法，Brückner[9]提出一种由PTZ(pan-tilt-zoom)相机组成的多相机系统内外参数的主动式自标定方法。2015年. Hastedt等[10]标定了无人机摄影测量中物体空间内方位参数，并分析了不同的主距离与不同主点对系统稳定性的影响.Zheng[11]研究了一种新的捆绑调整变焦镜头内参标定方法，通过建立关于变焦/聚焦内参新模型(变焦/聚焦相关内参共线方程)，定量分析了变焦镜头的不稳定性和变焦带来误差的联合影响.Zhigao[12]在主从双PTZ相机合作跟踪的视频监控中，提出一种新的框架，利用平面几何约束实现主从相机的合作跟踪，适用于监控基线宽、跟踪对象深度变化、场景动态变化的监控环境.

单一焦距下变焦镜头标定方法与普通相机标定类似.但变焦光学系统结构参数随着倍率、对焦和光阑孔径大小的调整而发生变化，为了能够更好地反映变焦镜头的变焦特性，需建立能更精确描述变焦特性的模型，标定变焦相机一般参数、变焦图像的缩放中心、不同焦距之间的光心位移.研究结果表明，厚透镜视觉模型具有更高的建模精度，更适合变焦光学成像系统的建模[13].

笔者研究了变焦相机的标定方法.首先，采用基于二消失点的自标定方法对变焦摄像机的两个固定焦距下的一般参数进行标定.然后对变焦图像进行SIFT特征匹配，根据匹配对建立直线方程，采用最小二乘方法估计缩放中心，变焦图像的缩放中心可用来进行深度估计.

1 变焦镜头的成像模型

由于针孔成像模型难以精确反映变焦光学系统结构参数(如焦距或倍率)变化与模型参数之间的关系.为了定性分析，常采用薄透镜模型和厚透镜模型.薄透镜模型能较好的解释像面、图像弥散与成像景深的关系，但制造理想镜头困难.对于变焦相机镜头，光学元件之间还存在相对运动，采用针孔模型和薄透镜模型都不能较准确地反映变焦相机的成像模型，因此采用厚透镜模型，如图1.平面H0xy和Hixy为主平面;H0和Hi分别为外光心和内光心;f0和fi分别为物距和像距.变焦时主平面H0xy和Hixy之间的距离会发生改变.

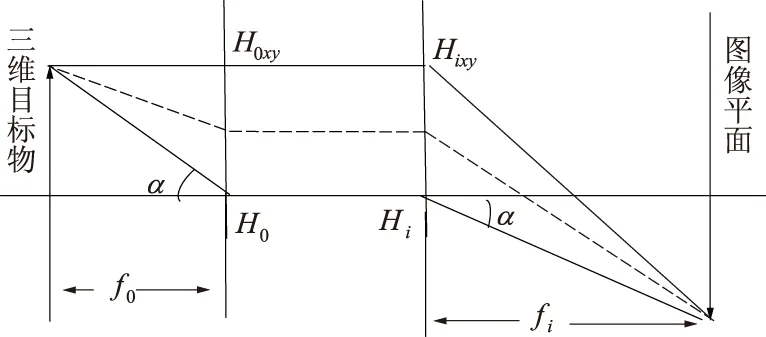
图1 厚透镜模型

2 一般参数的标定

一般参数的标定是指焦距、主点、畸变系数等常见摄像机参数的标定.笔者在一个固定的变焦镜头参数下，采用一种基于二消失点的自标定方法标定变焦相机两个焦距下的一般参数，并完成深度估计.将二消失点自标定结果与现有的Matlab标定工具箱对棋盘格模板进行标定、机器视觉软件Halcon采用标准实心圆阵列图案的标定结果进行比较.

2.1 确定消失点

基于二消失点的相机自标定要求场景中有两组相互正交的平行直线，如图2.场景中包含矩形图案ABCD，图像平面EFGH，O为相机的光心.假设EF和GH、EH 和FG方向上的消失点分别为M、N.根据矩形ABCD的几何特性和消失点的性质可得OM⊥ON，也就是说对两组相互正交的平行直线成像的相机光心，位于由这两组平行直线投影得到的两个消失点为直径的球上.

因此，只要检测出场景中的矩形投影到图像平面上的4个顶点的坐标，就可计算出消失点M和N的坐标.故图像平面上矩形的4个角点的正确检测和精确定位是相机标定能否正确实现的前提，同时也是决定标定精度的关键步骤.

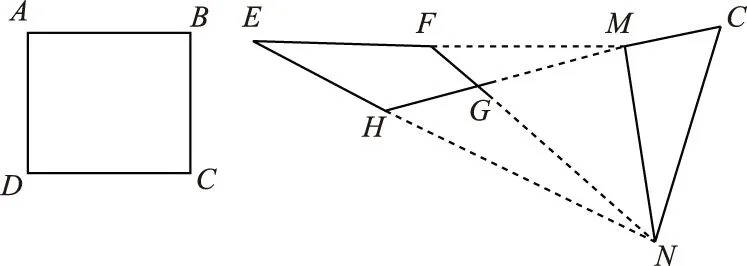
图2 矩形模板的消失点

2.2 基于Harris的亚像素角点检测

Harris算子是Harris等人提出的一种角点检测算法，该算法的检测结果是像素级的.为了提高相机标定精度，笔者引入迭代算法对Harris角点检测算法进行优化，获得亚像素级的角点坐标.

图3为笔者用于相机标定的棋盘格图像，棋盘格角点附近的点可以分为在边缘上的点和不在边缘上的点两类.P点处灰度梯度为零，而R点上的灰度梯度Ii方向与OR垂直，所以，在角点O附近点的灰度梯度均垂直于该点与角点的连线.

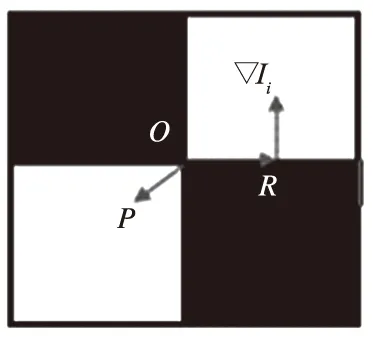
图3 棋盘格图像

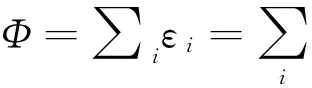
(1)

检测角点准确位置的问题转化为迭代优化问题

(2)

通过对初始Harris角点进行一定级数的迭代优化，就可以得到更精确的亚像素级角点坐标.

两种角点检测算法的结果对比如图4所示,其中‘•’表示Harris的角点检测位置，圆圈内‘×’表示笔者的角点检测位置，圆圈外‘+’表示角点实际位置.由图可以看出，亚像素的角点检测的算法更接近实际的角点位置.所以笔者采用基于Harris算法的亚像素级角点检测的方法，不仅提高了相机的标定精度，也提高了角点检测速度.

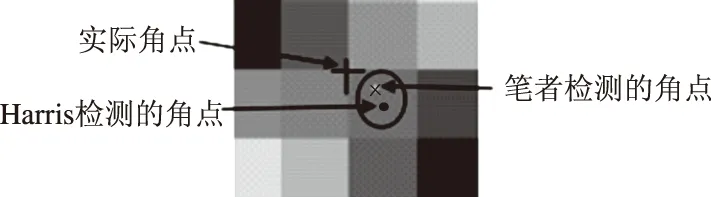
图4 两种角点检测方法的结果对比

2.3 相机内参数的线性求解

设在图像坐标系下由模板图像得到的两消失点为：M(um,vm)、N(un,vn)，则在相机坐标系下M、N的坐标为：M[(um-u0)dx,(vm-v0)dy,f]、N[(un-u0)dx, (vn-v0)dy,f]，由于相机光心位于由这两组平行直线投影得到的两个消失点为直径的球上，因此可得到关于内参数的约束方程

vm)(v0-vn)+1=0.

(3)

式(3)中有4个未知数fx、fy、u0、v0，在不考虑畸变的情况下，从不同角度拍摄4幅图片就可以线性求解相机的4个内参数.

3 缩放中心的标定

对于变焦镜头而言，必须考虑主点的变化或稳定性.不同变焦图像之间总存在一个相对的缩放中心，缩放中心的标定和计算方法对深度估计至关重要.首先需要对变焦图像进行匹配，得到若干匹配点对，再采用最小二乘方法估计缩放中心.

3.1 图像的SIFT特征匹配

SIFT是David G Lowe在1999年提出的基于不变量描述子的匹配算法，SIFT算法在光强变化、图像旋转、比例缩放、仿射变换等情况下，仍可以得到大量准确、稳定的 SIFT 特征点.

SIFT特征匹配算法主要包括以下部分：①构建尺度空间，检测极值点;②特征点过滤及精确定位,去除低对比度和对噪声敏感的候选关键点，去除边缘点;③确定关键点的方向参数,利用特征点领域像素的梯度方向分布特征来定关键点的方向;④生成特征向量描述子,利用特征点邻域像素梯度信息生成128维特征向量，建立图像特征描述符;⑤SIFT特征向量的匹配,采用特征向量的欧氏距离对SIFT的特征向量进行匹配.

3.2 估计缩放中心

理想情况下，以缩放中心为原点的图像坐标系中，匹配点的径向斜率相同.实际情况中由于成像畸变等因素的影响，即使正确的匹配点，径向斜率也不可能完全相同，因此通过给出一个合理的阈值来筛选比较理想的匹配点，尽量剔除那些因为匹配算法所造成的错误匹配.

假设对变焦图像进行SIFT特征匹配后得到n对匹配点，由一对匹配点确定一条直线，可获得n对匹配点的直线方程.理想情况下，缩放中心(Zx,Zy)经过每一条直线，则有矩阵方程

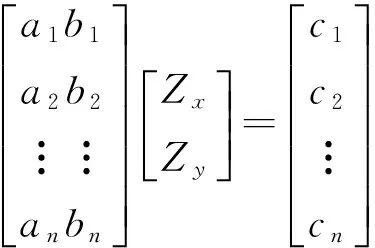
(4)

简写成

Aβ=c.

(5)

显然，求缩放中心β=(Zx,Zy)的问题可转化为最小二乘参数估计问题，即当N>2时，缩放中心β由下式唯一确定

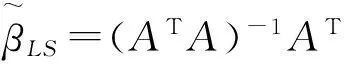
(6)

4 标定实验及结果分析

本实验使用普通手动变焦相机索尼SLT-A58作为获取图像的工具，镜头DT 3.5-5.6/18-55mm SAM II，像素尺寸8.4 μm×8.4 μm，分辨率选择2 736×1 824，变焦模式18～55 mm变焦环.

4.1 基于二消失点的变焦相机一般参数的自标定

Step1.获取图像.采集图像时，光圈固定，只聚焦一次，分别对场景中包含两组相互正交的平行直线的平面棋盘格模板、矩形地砖图案从不同角度分别拍摄20幅图像.每4幅图像做一组标定实验，如图5.得到5组实验结果，再求平均值.

图5 实验图像

Step2.图像预处理.图像的预处理主要是彩色图像灰度化处理和图像去噪处理.

Step3.角点检测.基于Harris算法的亚像素角点检测方法检测角点.为了减小镜头畸变对实验结果的影响，选取图案中间的矩形进行标定.

Step4.求取相机的内参.求得每幅图像的4个角点后，可由直线几何关系求得消失点，然后利用式(3)求解相机的内参数.

Step5.实验结果与分析.对平面棋盘模板、矩形地砖分别在焦距35、55 mm下，从不同角度分别拍摄20幅图像，每4幅图像一组做一次标定实验，得到5组实验结果，对5组实验结果取平均值，得到了相机内参数，如表1.

表1 基于二消失点自标定结果

为了验证本文中基于二消失点自标定结果的准确性，分别与机器视觉软件Halcon标定法、matlab工具箱的张正友标定法的结果做了比较，并列出了相机内参数的理论值，如表2所示.还分析了不同标定方法的相对误差，如表3所示.

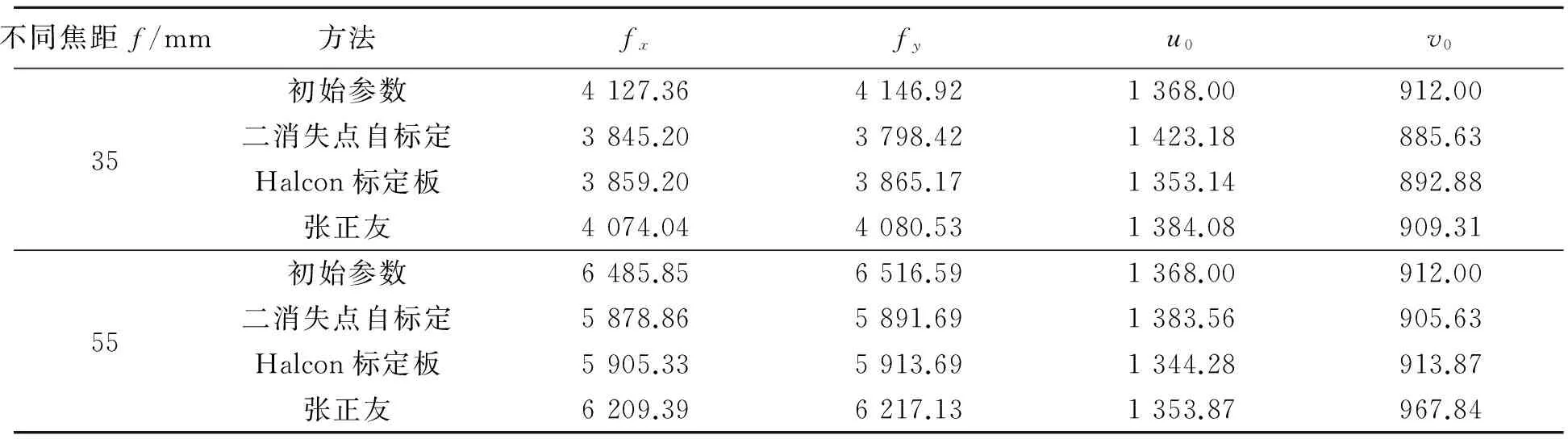
表2 标定结果对比

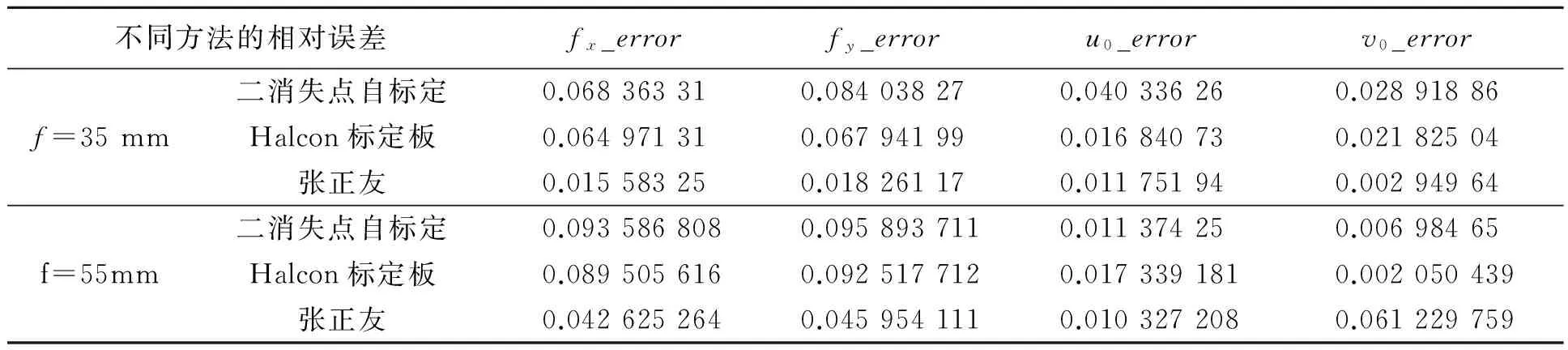
表3 相对误差

从表1、2、3可得，二消失点自标定结果和借助Halcon软件的标定板标定方法、张正友方法所标定的结果相当，说明了笔者算法具有较好的精度；对矩形地砖图案、棋盘格图案在不同焦距下进行标定，结果表明该方法简单，且对场景的约束不高.

为了验证二消失点标定法的鲁棒性，对图像加入0～3像素的噪声水平，在每个噪声水平下进行20次独立实验，重新计算相机参数，其均方根误差变化曲线如图6.从图6中可看出，相机内参数误差随噪声水平线性增大，但误差仍然比文献[14]和文献[15]的误差小得多，所以仍能较好地完成标定，说明二消失点自标定算法的鲁棒性较好.

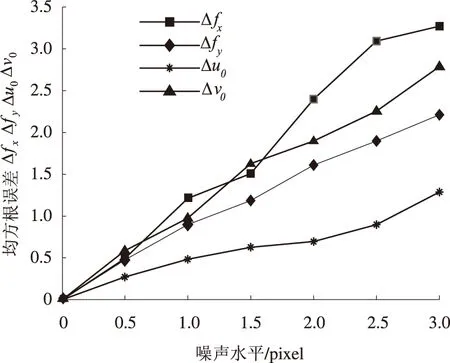
图6 标定结果的均方根误差曲线

4.2 缩放中心的标定

采集图像时，光圈固定，只聚焦一次，从不同角度拍摄了7组变焦图像，每组数据都包含F35和F55两个焦距下的变焦图像，如图7(a).对变焦图像进行SIFT特征匹配得到图7(b)，得到73对匹配点.利用式(6)估算变焦图像的缩放中心，如图8所示.

利用同样的方法对7组变焦图像进行缩放中心的标定，7组实验的缩放中心标定结果如图9.

图7 SIFT特征匹配

图8 缩放中心

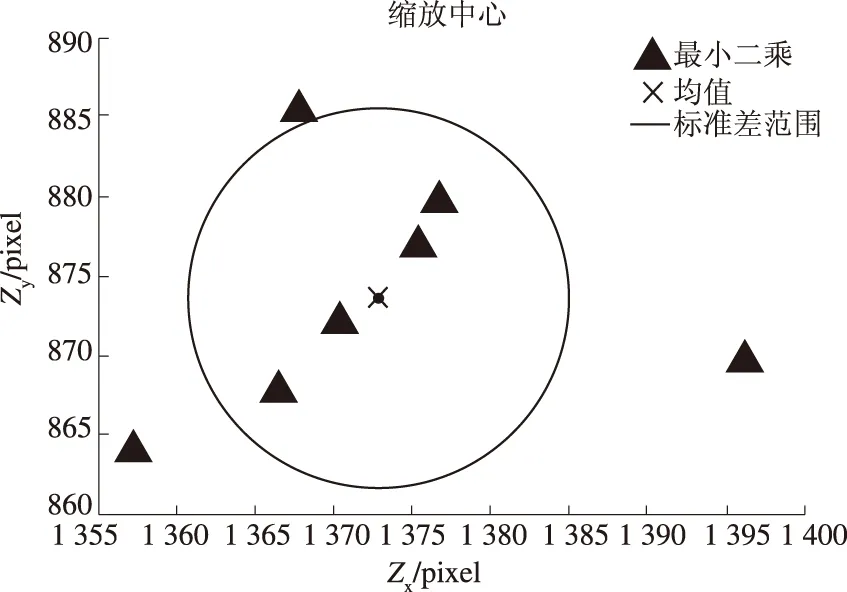
图9 缩放中心

4.3 光心位移的标定

平面棋盘格上各特征点的坐标为(xwi,ywi,zwi)，成像平面上的坐标为(xci,yci,zci)，图像坐标为(ui,vi).则摄像机的外参数模型为：

(8)

式中：s为深度系数；M为摄像机的四参数模型的内参数矩阵.根据Faugeras求取投影矩阵的方法求出H单应性矩阵：

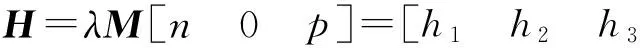
(9)

将已求出的内参数代入式(8)计算出摄像机坐标系相对于标定板上世界坐标系的外参数，而摄像机外参数中的平移向量就是变焦摄像机的外光心到世界坐标系原点的直线距离.因此通过标定板的一组变焦图像就能计算摄像机的光心位移.

标定板的变焦图像采用估算缩放中心时采集的7组变焦图像，图10为变焦镜头在两个不同焦距下的外光心分别到世界坐标系原点的深度值，即平移向量z轴的坐标值.

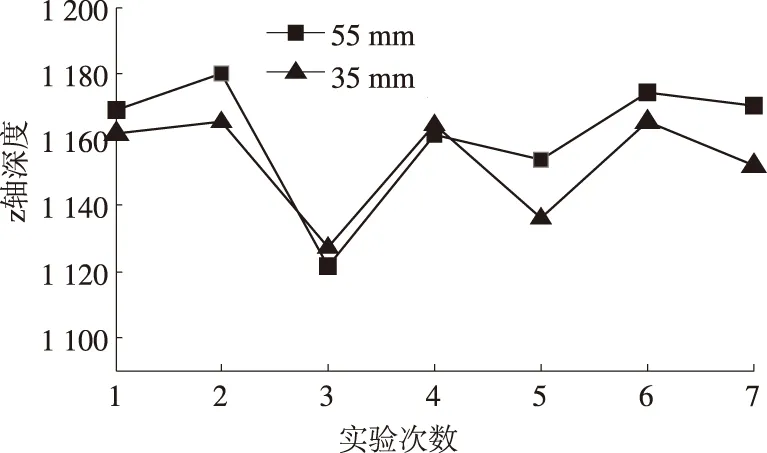
图10 平移向量z轴深度

图11则是焦距F35和F55之间光心位移标定结果的变化曲线.

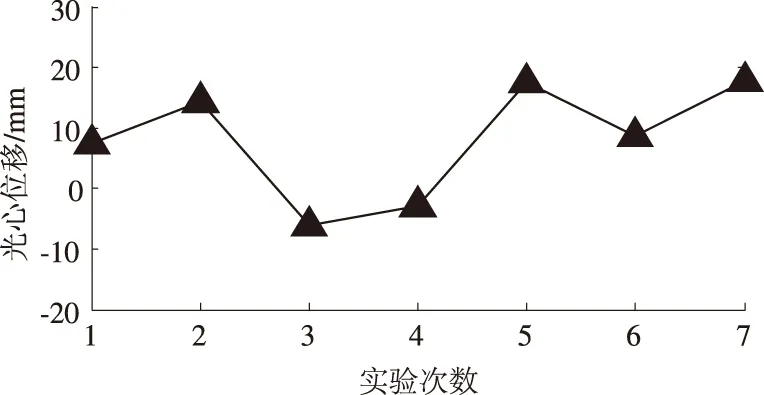
图11 光心位移

通过对7组实验的结果求平均值可得到光心位移标定结果为10.722 0 mm，所以光心位移与焦距的变化量有明显的差距，从而说明厚透镜模型更适合用来描述摄像机的变焦镜头.

5 结论

基于亚像素角点检测算法对变焦式相机在某一固定焦距下进行二消失点自标定，运用消失点的几何特性建立关于相机内参数的约束方程，求出相机的内参数，将二消失点法的标定结果与借助机器视觉软件Halcon标定板法标定的结果进行对比，结果验证了该方法的有效性和鲁棒性；同时本文还计算了变焦图像的缩放中心、光心位移，结果表明,厚透镜模型更适合用来描述摄像机的变焦镜头.另外，计算出的缩放中心为后续的深度测量、三维重建提供数据基础.

[1] 吴福朝.计算机视觉中的数学方法[M].北京:科学出版社，2008.

[2] 陈继华,李勇,田增国,等.基于机器视觉的机械式表盘自动读表技术的实现[J].郑州大学(工学报),2015，36(3):101-105.

[3] 邱茂林,马颂德，李毅.计算机视觉中相机定标综述(J).自动化学报,2000,26(1): 43-55.

[4] BASU A.Active calibration:Alternative strategy and analysis(C) //Proc.IEEE Conf.On Computer Vision and Pattern Recognition, 1993:495-500.

[5] 孟晓桥，胡占义.摄像机自标定方法的研究与进展[J].自动化学报，2003,29(1):110-122.

[6] 张雪波,路晗,方勇纯,等.室外环境下PTZ摄像机全自动标定技术及其应用[J]. 机器人,2013,35(04):385-393.

[7] 石皓,赖世铭,刘煜，等.一种用于鱼眼PTZ主从监控系统的标定方法[J].系统仿真学报,2013,25(10):2412-2417.

[9] Brückner M, Bajramovic F, Denzler J. Intrinsic and extrinsic active self-calibration of multi-camera systems. machine vision & applications [J]. Fe. 2014,25(2):389-403.

[10]HASTEDT H,LUHMANN T.Investigations on the quality of the interior orientation and its impact in object space for UAV photogrammetry[J].The International Archives of the Photogrammetry, 2015, XL.1(W4):321-328.

[11]ZHENG S, WANG Z, HUANG R. Zoom lens calibration with zoom-and focus-related intrinsic parameters applied to bundle adjustment[J]. ISPRS Journal Of Photogrammetry & Remote Sensing.2015(102):62-72.

[12]Zhigao C, Aihua L,Guoyan F,et al.Cooperative object tracking using dual-pan-tilt-zoom cameras based on planar ground assumption.IET Computer Vision [J].2015,9(1):149-161.

[6] LAVEST J M, RIVES G, DHOME M. Three-dimensional reconstruction by zooming[J]. IEEE Transactions on Robotics and Automation,1993,9(2): 196-207.

[7] 李华，吴福朝，胡占义.一种新的线性相机自标定方法[J]. 计算机学报，2000,23(11):1122-1128.

[8] 胡钊政,谈正.一种基于二消失点的相机自标定新算法[J].空间电子技术,2005,23(1): 42-46.

Research on Self Calibration Method of Zoom Camera

ZHAO Shujun, DUAN Shaoli, ZHANG Xiaofang, LI Lei, LIU Xiaomin

(School of physics and Engineering, Zhengzhou University, Zhengzhou 450001, China)

In this paper, the calibration methods of camera zoom is studied. The self calibretion method based on two vanishing points is used to calibrate the general parameters of zoom camera.Compared with the results of two methods of Zhang Zhengyou and the machine vision software Halcon, the feasibility and robustness of the method in this paper is verified. In order to better reflect the characteristics of the zoom camera, a thick lens model selected can describe the zoom camera more accurately.The linear equations can be established according to feature correspondences obtained by the method based on SIFT feature matching between zoom images, and then the zoom center can be identified with the least square method.In addition, the optical center displacement can also be calculated between different focal length. The experimental result shows that the variation between optical center displacement and focal length has a apparent significant gap, so that the thick lens model is more suitable to describe the zoom camera.

Zoom camera calibration; Two vanishing point; Sub-pixel corner detection; Zoom center; The optical center displacement

2016-02-08；

2016-06-18

国家自然科学基金资助项目(61307019、11404290);河南省科技攻关计划重点项目(132102210396);河南省科技合作项目(152106000045);河南省基础与前沿技术研究项目(142300410225);河南省科技开放合作项目(152106000045)

刘晓旻(1973—),女,河南郑州人，郑州大学副教授,博士,主要从事光学精密检测与3D成像技术研究,E-mail:liumamara@zzu.edu.cn.

1671-6833(2016)05-0091-06

TB82

A

10.13705/j.issn.1671-6833.2016.05.018