基于数值计算的矩形孔蜂窝梁应力分布规律研究

王 衡，陈廷国

(大连理工大学 土木工程学院，辽宁 大连 116024)



基于数值计算的矩形孔蜂窝梁应力分布规律研究

王 衡，陈廷国

(大连理工大学 土木工程学院，辽宁 大连 116024)

通过有限元软件ANSYS对矩形孔蜂窝梁进行弹性分析，研究蜂窝梁应力分布规律，主要包括桥墩横截面正应力和剪应力分布、桥墩纵截面正应力分布及梁桥横截面正应力分布.另外，详细研究了跨高比、孔高比、长高比和距高比等因素对墩心横截面正应力和剪应力分布的影响.

矩形孔蜂窝梁；有限元；应力分布；影响因素

0 引言

蜂窝梁是一种新型钢结构构件，有两种常用制作方法：一种是将工字钢或H型钢按照一定的折线或弧线进行切割，然后错位焊接而成[1]；另一种是直接在工字钢或H型钢的腹板上开孔制成.与原型实腹梁相比，承载力相同时，蜂窝梁能够节省钢材25%～30%，且质量轻、安装方便[2～4].蜂窝梁开孔也为铺设管道提供了便利.

蜂窝梁包括空腹和实腹部分，如图1所示，在空腹部分处，由上翼缘(或下翼缘)和部分腹板组成的T型截面称为梁桥；整个实腹部分称为桥墩，桥墩中心简称墩心；梁桥和桥墩连接处称为桥趾[5].矩形孔蜂窝梁孔洞高度为d，孔洞长度为a，孔洞之间的距离为s，蜂窝梁高度为h，长度为l，则孔高比d/h、长高比a/h和距高比s/h是影响蜂窝梁受力性能的主要因素[6].

相对于国外，国内对蜂窝梁的研究较晚[7～8]，且在规范中没有相应的设计条文，这在很大程度上制约了蜂窝梁的工程应用[9].所以笔者对矩形孔蜂窝梁应力分布规律进行了研究，其结果可为工程设计提供参考.

1 有限元建模

笔者采用有限元软件ANSYS对蜂窝梁建模计算[10]，选择I10工字钢，根据不同参数要求在腹板上进行开孔而制成蜂窝梁.

蜂窝梁模型采用壳单元shell93模拟[2].笔者只对蜂窝梁弹性阶段进行受力分析，建模时忽略了焊缝及残余应力对结构的影响.其中蜂窝梁采用Q235钢，材料弹性模量取200 GPa，泊松比取0.3，屈服强度为235 MPa.

采用控制变量法分析各因素对蜂窝梁墩心横截面应力分布的影响，分别计算了d/h=0.3～0.8、a/h=0.3～1.2、s/h=0.3～1.2时的应力分布.如图2所示矩形孔蜂窝梁有限元模型.

2 应力分布规律

蜂窝梁应力分布与实腹梁的不同之处，主要体现在以下几个断面(图1所示)，即桥墩横截面(1-1断面，截面为工字型)、桥墩纵截面(2-2断面，截面为矩形)、梁桥横截面(3-3断面，截面为T形).

图2 矩形孔蜂窝梁有限元模型

2.1 桥墩横截面正应力和剪应力分布

取d/h=a/h=s/h=0.7、l/h=14的简支蜂窝梁进行详细研究，在跨中施加1 kN的集中荷载.取7l/10处桥墩中心横截面为初始位置，沿着梁长方向每隔0.01 m取一个断面，提取各节点应力.为方便分析，将各断面应力转化为截面单位弯矩(或单位剪力)作用下的正应力(或剪应力)，如图3所示为部分断面单位弯矩下的正应力曲线，图4为部分断面单位剪力下的剪应力曲线.结果表明：在墩心横截面两侧对称位置，正应力近似对称分布，剪应力分布近似相同；桥墩各横截面应力分布规律不同；距离孔口越近，应力集中越明显，在桥趾附近区域产生较大的正应力和剪应力；墩心横截面正应力分布不符合平截面假定，通过回归分析，正应力分布近似为三次曲线，剪应力分布为二次曲线，表达式分别为

σx=[-7.01(y/h)3-0.65(y/h)]σ0.

(1)

τ=[-21.45(y/h)2+2.83]τ0.

(2)

式中：y为验算点距离截面形心的高度，m；h为梁高，m；σx为正应力，MPa；σ0为按当量实腹梁(与桥墩横截面相同的实腹梁)计算截面单位弯矩下产生的最大正应力；τ为剪应力，MPa；τ0为按当量实腹梁计算截面单位剪力下产生的最大剪应力.

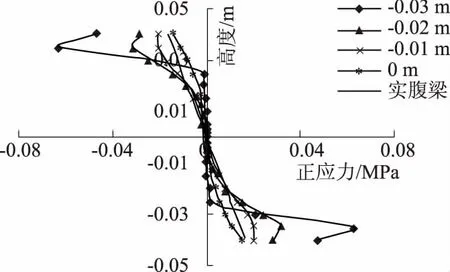
图3 桥墩横截面单位弯矩下的正应力曲线

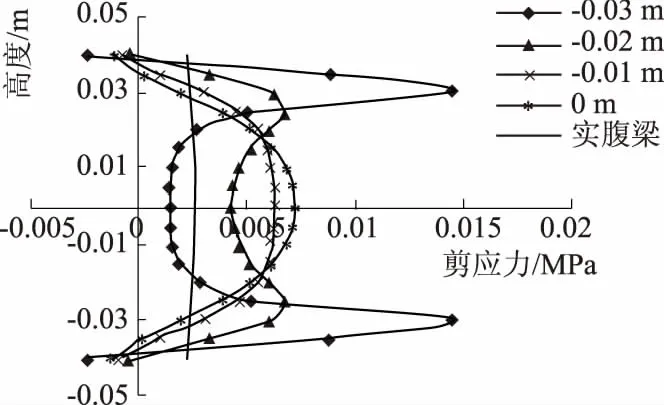
图4 桥墩横截面单位剪力下的剪应力曲线

取d/h=a/h=s/h=0.7的蜂窝梁进一步分析，当集中荷载作用于梁上任一位置时，墩心横截面正应力和剪应力分布规律不变；当两个对称集中荷载作用时，纯弯段梁和非纯弯段梁上墩心横截面正应力分布规律仍然相同，非纯弯段梁上墩心横截面剪应力分布规律也相同.由此得出，墩心横截面正应力和剪应力分布与荷载位置无关.

对于浅梁，当蜂窝梁孔数改变，即梁跨高比l/h改变时，墩心横截面正应力和剪应力分布几乎不变；而对于深梁，应力分布却发生了改变，图5和图6所示分别为不同跨高比时墩心横截面正应力和剪应力分布.由此得出：在计算蜂窝浅梁(l/h>5)时，墩心横截面正应力和剪应力分布与跨高比无关.

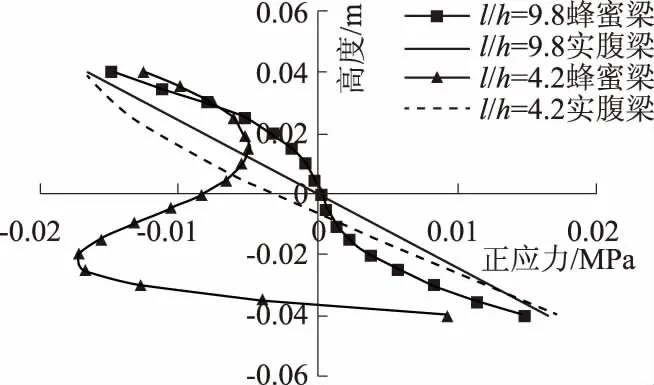
图5 不同跨高比时正应力分布

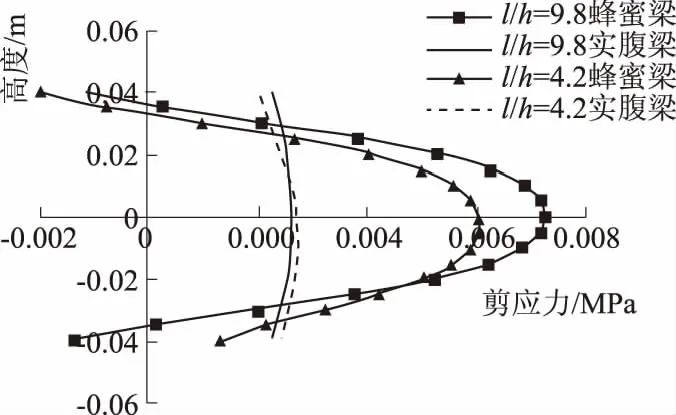
图6 不同跨高比时剪应力分布

取a/h=s/h=0.7不变，分别计算孔高比d/h=0.3～0.8时的应力分布情况，如图7和图8所示分别为不同孔高比时墩心横截面正应力和剪应力分布.由图可知：孔高比越小，墩心横截面正应力分布越趋近于线性，但正应力最大值相差不大；剪应力峰值均出现在腹板中心，随着孔高比减小，剪应力峰值减小；当孔高比趋近于零时，应力分布与实腹梁近似相同.

图7 不同孔高比时正应力分布

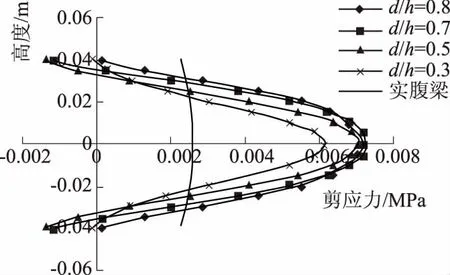
图8 不同孔高比时剪应力分布

取d/h=s/h=0.7不变，分别计算长高比a/h=0.3～1.2时的应力分布情况，如图9和图10所示分别为不同长高比时墩心横截面正应力和剪应力分布.由图可知：长高比对墩心横截面正应力分布影响很小，而对剪应力分布影响较大；随着长高比增大，剪应力峰值变大；当长高比趋近于零时，应力分布与实腹梁近似相同.

取d/h=a/h=0.7不变，分别计算距高比s/h=0.3～1.2时的应力分布情况，如图11和图12所示分别为不同距高比时墩心横截面正应力和剪应力分布.由图可知：距高比越大，墩心横截面正应力分布越趋近于线性，但正应力最大值相差不大；在距高比较小时，腹板靠近中心部分区域正应力几乎为零；距高比对剪应力分布影响较大，距高比越大，剪应力峰值越小，但减小速率变小，剪应力分布越均匀；当距高比趋近于无穷时，应力分布与实腹梁近似相同.所以，在工程设计时，蜂窝梁孔洞之间的距离不宜过小.

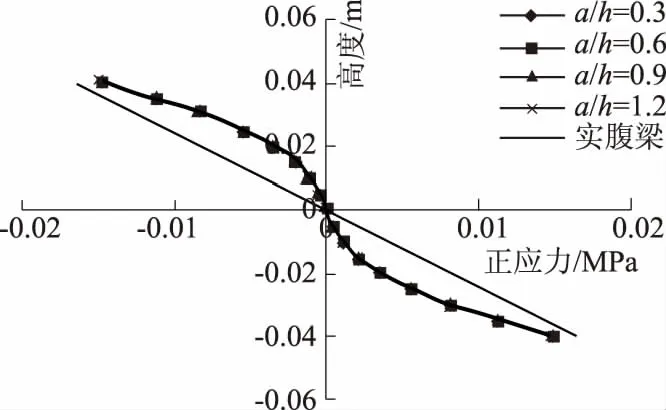
图9 不同长高比时正应力分布

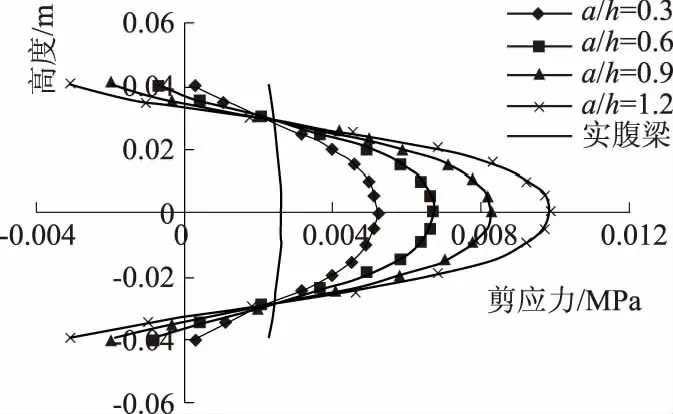
图10 不同长高比时剪应力分布

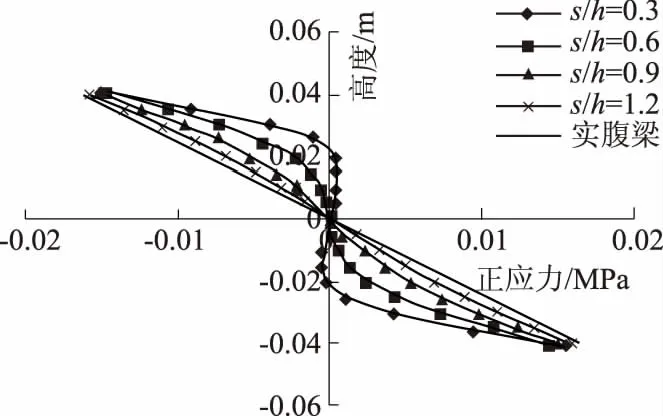
图11 不同距高比时正应力分布

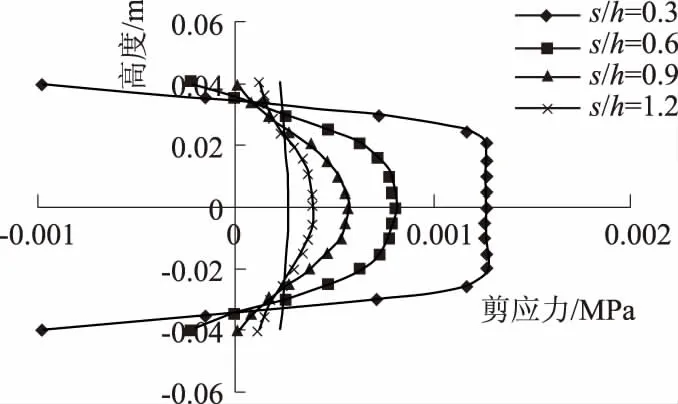
图12 不同距高比时剪应力分布

2.2 桥墩纵截面正应力分布

取d/h=a/h=s/h=0.7、l/h=14的蜂窝梁进行研究，为消除集中荷载作用位置应力集中的影响，在距离支座和集中荷载较远位置，即选择7l/10处桥墩进行分析.沿着桥墩高度方向，每隔0.01 m取一个纵截面分析正应力.计算发现，在腹板中心上下对称位置处桥墩纵截面正应力为对称分布，所以选取一半桥墩详细分析，图13所示为以桥墩高度中心为坐标原点的各纵截面正应力分布.然后将各纵截面上的应力进行积分，求出截面弯矩，图14所示为沿高度方向桥墩纵截面弯矩分布.

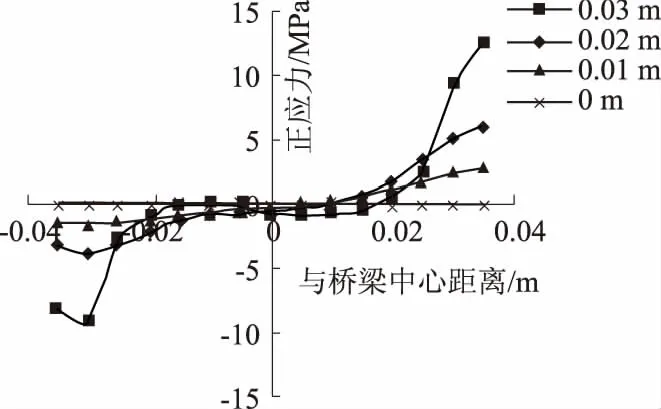
图13 桥墩不同高度处的纵截面正应力分布

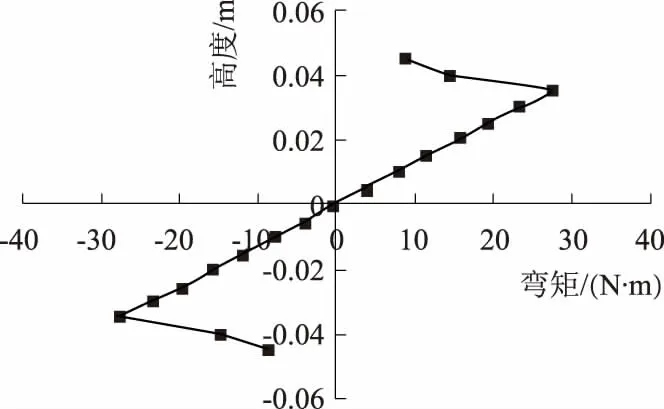
图14 沿蜂窝梁高度方向桥墩纵截面弯矩分布

根据图13不难发现：沿着梁高方向，不同高度处桥墩纵截面正应力分布为非线性，且截面最大正应力出现在孔洞附近.而由图14可知：沿着梁高方向，在-d/2～d/2范围内，桥墩纵截面弯矩为线性分布，桥墩腹板中心处纵截面弯矩为零.在费氏空腹桁架法原理[3]中，假设桥墩中心为反弯点，通过以上分析，验证了该假设的正确性，可为蜂窝梁挠度计算方法研究提供参考.

2.3 梁桥横截面正应力分布

取d/h=a/h=s/h=0.7、l/h=14的蜂窝梁进行研究，提取3l/4+a/2段梁桥各横截面上正应力分析，结果发现：梁桥横截面正应力呈线性分布，仅在桥趾附近有点差异.图15所示为沿着孔洞长度方向，梁桥翼缘正应力分布.根据费氏空腹桁架法原理[3]，假设梁桥中心为反弯点，梁桥横截面正应力由两部分组成：梁弯矩正应力和剪力引起的次弯矩正应力.

假定蜂窝梁空腹截面受到的剪力为Vi，则孔洞上下两个梁桥横截面各承担剪力Vi/2；以孔洞中心断面为坐标原点，设梁桥上任一位置与坐标原点距离为xi，则由剪力引起的次弯矩为Vixi/2；所以梁桥横截面上正应力可表示为

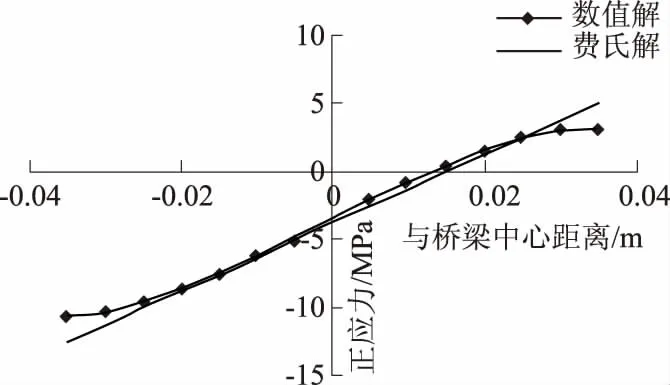
图15 沿孔洞长度方向梁桥翼缘正应力分布

(3)

式中：Mi为以蜂窝梁为计算结构，验算截面位置所受的弯矩；y为验算位置距离蜂窝梁截面形心的高度；Iz为蜂窝梁空腹截面惯性矩；y′为验算位置距离梁桥T型截面形心的高度；IT为梁桥T型截面惯性矩.

由图15可知，利用式(3)计算所得梁桥翼缘正应力分布与数值计算结果比较接近，验证了该式的正确性，同时可为蜂窝梁挠度计算方法研究提供参考.

3 结论

利用有限元软件ANSYS对矩形孔蜂窝梁应力分布进行了研究，得出如下主要结论：

(1)由于受到孔洞影响，蜂窝梁上的应力分布与实腹梁有很大区别，在计算分析时应加以区分.

(2)蜂窝梁桥墩横截面正应力和剪应力分布与距离孔洞远近有密切关系，距离孔口越近，应力集中越明显.墩心横截面正应力分布不符合平截面假定，而是接近三次曲线；剪应力分布为二次曲线，腹板中心剪应力最大，两边较小.

(3)墩心横截面正应力和剪应力分布与荷载作用位置、跨高比无关，而孔高比、长高比和距高比对应力分布影响较大.孔高比越小、长高比越小、距高比越大，墩心横截面应力分布越接近与实腹梁.

(4)桥墩纵截面正应力分布与高度有关，为非线性分布，但纵截面弯矩在孔洞范围内沿梁高方向呈线性分布，桥墩中心为反弯点.

(5)梁桥横截面正应力呈线性分布，并且由梁弯矩正应力和剪力次弯矩正应力叠加而成，从而验证了费氏空腹桁架原理对梁桥正应力计算的正确性.

[1] 贾连光, 孙宏达, 王春刚. 蜂窝式钢框架结构抗震性能试验研究[J]. 工程力学, 2012, 29(7): 147-153.

[2] 李鹏飞, 姚谦峰. 蜂窝梁应力和挠度计算方法[J]. 建筑结构, 2011, 42(2)： 52-55.

[3] 倪富生, 胡泰祥, 胡嗣元, 等. 蜂窝梁的应力分布及设计计算探讨[J]. 工业建筑, 1984, 24(8)： 27-35.

[4] 王洪范, 王立新. 蜂窝梁的应用和计算方法[J]. 工业建筑, 1994, 24(8)： 3-4.

[5] 曾欢艳. 考虑孔高比和距高比正六边形孔蜂窝梁挠度计算研究[D]. 长沙：湖南大学土木工程学院, 2013.

[6] 蒋上. 正八边形孔蜂窝梁的挠度计算研究[D]. 长沙：湖南大学土木工程学院, 2011.

[7] 罗烈, 罗晓霖. 蜂窝梁设计规范的比较研究[J]. 建筑钢结构进展, 2005, 7(2)： 43-47.

[8] CHEN J K, KIM B, LI L Y. Analytical approach for transverse vibration analysis of castellated beams[J]. International journal of structural stability and dynamics, 2014, 14(3)： 96-100.

[9] 刘鑫. 考虑孔况影响的蜂窝梁设计计算研究[D]. 长沙：中南大学土木工程学院, 2006.

[10]CHUNG K F, LIU T C H, KO A C H. Investigation on vierendeel mechanism in steel beams with circular web openings[J]. Journal of contractual steel research, 2001, 57(5)：467-490.

Research on the Stress Distribution of Rectangular Hole Castellated Beams Based on Numerical Calculation

WANG Heng, CHEN Tingguo

(School of Civil Engineering, Dalian University of Technology, Dalian 116024, China)

According to the elastic analysis of rectangular hole castellated beams by using the finite element software ANSYS, the stress distribution of castellated beams was studied, which mainly included normal stress and shearing stress distribution of pier cross section, normal stress distribution of pier longitudinal section and normal stress distribution of beam bridge. In addition, the factors affecting the normal stress and shearing stress distribution of the center of pier cross section were studied in detail, which contained span-depth ratio, width-depth ratio, length-depth ratio and space-depth ratio. The research could provide reference for engineering design.

rectangular hole castellated beam; finite element; stress distribution; factor

2015-11-20；

2016-01-19

陈廷国(1957—)，男，辽宁大连人，大连理工大学教授，博士，博士生导师，主要从事大型及新型结构研究，E-mail：chentg@dlut.edu.cn.

1671-6833(2016)06-0058-05

TU391

A

10.13705/j.issn.1671-6833.2016.03.029