一类非凸多目标优化问题的同伦算法
李金燕,金 星,贺 莉*
(1.长春工业大学 基础科学学院,吉林 长春 130012;2.长春医学高等专科学校 药学系,吉林 长春 130031)
一类非凸多目标优化问题的同伦算法
李金燕1,金 星2,贺 莉1*
(1.长春工业大学 基础科学学院,吉林 长春 130012;2.长春医学高等专科学校 药学系,吉林 长春 130031)
给出一类非凸区域的拟法锥构造方法,并在该可行域上建立多目标优化问题的KKT点组合同伦方程,证明了同伦算法的整体收敛性,数值例子说明此方法是可行和有效的。
多目标规划; 拟法锥条件; 同伦方法
0 引 言
同伦方法是求解优化问题的一种重要算法[1-4]。目前,利用同伦内点法求解一般凸多目标规划的最小弱有效解已有很多成果[5-7],但在实际生活中很多关于多目标规划问题的可行域都是非凸的[8],对于不同的非凸区域,需要满足一定的边界条件。当可行域满足拟法锥条件时,构造相应的正独立映射函数至关重要[9],文献[8]并没有给出具体的构造方法。事实上,非凸区域的拟法锥构造并没有统一的方法,只能针对具体的某一类进行研究。文献[10]介绍了一类部分反向凸约束区域的拟法锥构造问题,文献[11]给出了由球体和分片线性函数构成的非凸区域的拟法锥构造。文中在文献[10-11]的基础上针对“N”型非凸区域给出拟法锥构造,并在该可行域上用同伦算法求解多目标优化问题。
文中考虑如下的多目标优化问题:
(1)
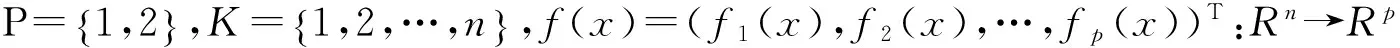
文中使用如下记号:
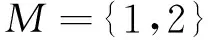
式中:﹟B1(x)——指标集B1(x)的元素个数;
﹟B2(x)——指标集B2(x)的元素个数;
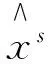
对于(VP),考虑如下的非凸规划问题:
引理1 (VP1)的最优解一定是(VP)的弱有效解。
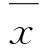
显然(VP1)是一个含有n+p个变量的非凸规划问题,(VP1)的KKT方程为:
(3)
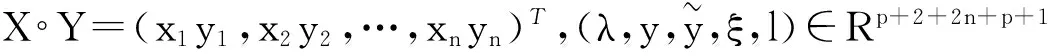
引理2[10]
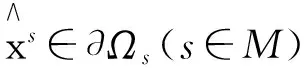
2)∀x∈∂Ωs(s∈M),有{x+l。
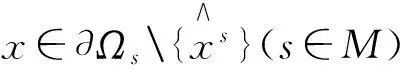
文中做如下基本假设:
(C1)Ω是有界连通集,且Ω0非空;
(C2)∂Ω是正独立的,即∀x∈∂Ω,gs(x)(s∈B1(x)),hjk(x)((j,k)∈B2(x))线性正独立。
1 正独立映射及拟法锥条件
对于问题(2),构建关于约束梯度的正独立映射如下:
(4)
下面给出映射(4)关于约束梯度正独立的引理。
定理1 由式(4)定义的映射{ηs(x),ηjk(x)}关于{gs(x),hjk(x)}(s∈M,j∈P,k∈K)是正独立的,即∀x∈∂Ω,若
(5)
必有ys=αs=yjk=αjk=0。
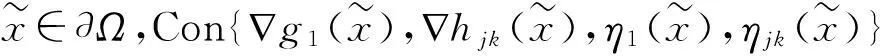
令
作超平面
对∀a>0,令
则
所以Hjk(z(2))>0。
因为
所以
所以z(1),z(2),z(3)在Hjk(x)的同一侧,即Con{,是尖凸锥。
定理2(拟法锥条件) 定理1中构造的正独立映射{ηs(x),ηjk(x)},(s∈M,j∈P,k∈K),对∀x∈∂Ω有
(7)
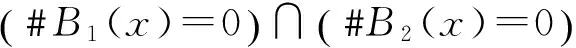
所以
故有
得证。
2 同伦方程及收敛性
对于式(3)构造同伦方程如下:
(8)
其中,
当t=1时,同伦方程(8)有唯一解
当t=0时,式(8)变为(VP1)的KKT系统(3),因此同伦方程(8)的解就是(VP1)的KKT系统(3)的解,令
(9)
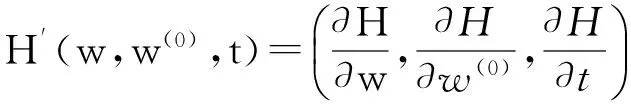
(10)
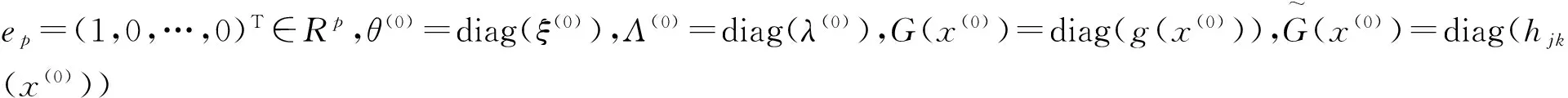
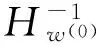
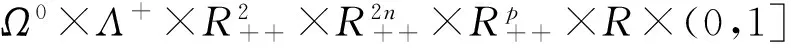
证明类似于文献[5]。
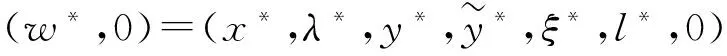
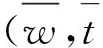
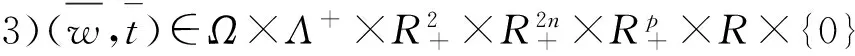
由于H(w(0),1)解是唯一的,故情况1)不成立。若情况2)成立,必存在子列(w(k),tk)∈Γw(0),使得gso(x(k))→0(存在某个1≤so≤2)或hjoko(x(k))→0(存在某个(jo,ko),1≤j0≤2,1≤k0≤n),‖y(k)‖→或‖‖→,这与引理4矛盾,所以情形2)不成立,故仅有情形3)成立。显然是式(8)的一个解,这就证明了存在性。如果Γw(0)是有限的,此极限点是Γw(0)的另一个端点,记为,则得到是式(8)的一个解。
3 算法及数值例子
如果用Γw(0)上曲线的弧长u作为该曲线的同伦参数,即存在连续可微函数w(u),t(u),使得
(11)
由微分式(11)得:
定理4 同伦路径Γw(0)由下面常微分方程初值问题确定:
(12)
如果有t(u*)=0,则w*是KKT方程的解。
例子:
计算结果见表1。

表1 计算结果
[1] 林正华,李勇,于波.一般非线性规划的组合同伦内点法[J].应用数学与计算学报,1996,80:209-224.
[2] 刘国新,冯果忱,于波.解序列极大极小问题的凝聚同伦方法[J].吉林大学学报:理学版,2003,41(2):155-156.
[3] 于波,冯果忱,张绍梁.非凸非线性规划的凝聚约束同伦算法[J].非线性分析,2001,45:839-847.
[4] Lin Z H,Zhu D L,Sheng Z P. Finding a minimal efficient solution of a convex multiobjective program [J]. Optim Theory Appl.,2003,118(3):587-600.
[5] 刘庆怀,林正华.求解多目标规划最小弱有效解的同伦内点方法[J].应用数学学报,2000,23(2):188-195.
[6] Shang Y F,YU B. A constraints shifting homotopy method for convex multiobjective programming [J]. Compute and Appl. Math.,2011,236(5):640-646.
[7] 贺莉,谭佳伟,陈嘉,等.混合约束多目标优化问题的凝聚同伦内点方法[J].吉林大学学报:理学版,2014,52(2):212-218.
[8] 杨轶华,赵立芹,吕显瑞,等.求多目标拟锥条件下最小弱有效解的同伦内点算法[J].吉林大学学报:理学版,2007,45(1):35-38.
[9] 张春阳,张国霜,李卓识,等.正独立映射的判定及其在非凸优化中的应用[J].长春工业大学学报:自然科学版,2010,31(1):111-114.
[10] 高云峰,刘庆怀.一类部分反向凸约束优化问题的组合同伦方程[J].吉林大学学报,2008,11:1110-1112.
[11] 李洪伟,刘庆怀.一类复杂非凸区域的拟法锥构造方法及其在非凸规划求解中的应用[J].应用数学学报,2009(5):400-412.
Homotopy method for a class of non-convex multiobjective programming problems
LI Jinyan1,JIN Xing2,HE Li1*
(1.School of Basic Science,Changchun University of Technology,Changchun 130012,China;2.Phamacy Department,Changchun Medical College,Changchun 130031,China)
We give a method to construct the quasi-normal cone in a class of non-convex regions in which the combined K-K-T points homotopy equation of the multi-objective programming problem is built up. It is proved that the method is with global convergence property by means of numerical examples.
multi-objective programming; quasi-normal cone condition; homotopy method.
2016-04-30
吉林省自然科学基金资助项目(20130101061JC)
李金燕(1990-),女,汉族,山西临汾人,长春工业大学硕士研究生,主要从事最优化理论与算法方向研究,E-mail:jinyan_yiyi@126.com. *通讯作者:贺 莉(1970-),女,汉族,吉林图们人,长春工业大学教授,硕士,主要从事最优化理论与算法方向研究,E-mail:heli_xu@126.com.
10.15923/j.cnki.cn22-1382/t.2016.5.02
O 221.6
A
1674-1374(2016)05-0422-06

