基于正交设计的露天转地下空区变形预测及可靠度分析

陈佳耀，史秀志，周 健，邱贤阳



基于正交设计的露天转地下空区变形预测及可靠度分析

陈佳耀，史秀志，周 健，邱贤阳

(中南大学资源与安全工程学院，长沙410083)

科学分析地下采空区稳定性是实现铜绿山露天矿Ⅰ号矿体残矿安全高效回采的关键，考虑将间柱宽度、空区跨度、境界顶柱厚度、尾砂堆高等4个影响因素进行正交设计并运用FLAC3D模拟试验，对49组试验结果进行极差、方差及回归拟合分析，并结合安全系数与可靠度指标对残矿回采安全与效益进行评估。结果表明：4个因子与位移量、安全系数的拟合度较高，相关系数2≥0.952，建立一个反映4因素下空区位移的综合数学预测模型，结合工程应用证明预测模型的有效性；影响采空区稳定性的显著程度依次为＞＞＞；并对比0.05与值，得到重要性排序为>>>，且均为不可忽视的重要因素；4个因子可靠度指标在≥1.7时收敛开始于某值，此时安全系数与可靠度之间可达最优化，且收敛值大小满足＞＞＞。

正交试验；可靠度指标；数值模拟；露天坑堆尾；境界顶柱；

采空区顶板稳定性是露天转地下开采矿山面临的最大问题之一，在预留境界顶柱高度、露天坑承载量、空区跨度、间柱厚度等发生变化时，采空区均可能垮塌，影响因素本身具有复杂性、未知性等特征，稳定性的分析评价困难，可靠度指标模糊，且随着开采向深部延伸，以上问题将愈发显著，这给矿山生产和安全带来巨大的隐患[1−6]。国内外就采空区稳定性分析研究的方法很多，其中，传统的半定量分析空区稳定性的方法有经验类比法、按破裂拱概念及松散系数理论估算法、K.B.鲁佩涅依特理论估算法和厚跨比法等，但传统方法考虑因素单一、系统性差。一些关于局部因素相关关系的研究也获得了较大的成果，包括张思敏等[7]利用RFPA方法对顶板垮塌、损伤进行数值模拟，计算垮塌发生时空区临界跨度和顶板安全厚度之间的关系；邓清海等[8]通过使用地表移动GPS监测数据并结合实验模拟，分析了露天采坑围岩移动、变形规律等；赵延林等[9]利用突变理论下的强度折减，通过拟合曲线函数表明复杂空区条件下的顶板厚跨比及跨度对顶板稳定性的双重影响；吴启红等[10]提出多级模糊评判与数值模拟相结合方式进行多空区稳定性评价。

虽然文献[7−10]中的方法优于传统分析法，但仍无法解决多因素多变量系统分析的困难，相反地，若逐一分析多变量，则试验困难、工作量大，难以分析结论，正交设计是可用于多影响因素综合分析，同时能在保证结果客观正确的基础上减少试验次数的一种方法[11−13]，可满足复杂地质条件和多影响因素下的空区稳定性综合评价。同时，为进一步建立安全系数评判指标，利用可靠度指标可得各因子影响下空区的可靠度关系，可靠度是建立在安全系数的基础上进行综合评判的指标[14−18]。

为解决多因子影响和可靠度预测指标问题，应用正交试验和数值模拟结合，对铜绿山Ⅰ号矿体残矿回采采空区稳定性进行预测，并利用改进的一次二阶矩法验算点法(AFORM)[19]进行可靠度分析，在达到可靠度指标的基础上，实现稳定性安全系数和经济效益的最优化。针对铜绿山利用露天坑干堆尾砂回填的实际，列出综合考虑影响地下复杂双采空区稳定性的4个因素：间柱宽度、空区跨度、境界顶柱厚度和尾砂堆高，并对Ⅰ号矿体下的试验采场进行稳定性验证和可靠度评价。

1 采空区变形影响因素及计算方法

铜绿山I 号矿体目前已闭坑，形成 2×105m2南坑暴露面积，为合理利用空间，自2007年开始进行回填尾砂，目前已累积达20 m，I 号矿体主要赋存于−305~−185 m，平均走向 110 m，厚 50 m，倾角60°~ 80°，以40 m为1中段采用盘曲机械化上向水平分层胶结充填为采矿法回采，每个分层高度均为 3 m。为保证回采连续性，各中段均采用2采1充方式，保证空区暴露面积为 6 m及以下。

为分析露天转地下矿山在地下回采过程中空区稳定性，采用正交试验设计数值模拟分组，并通过模拟结果对空区变形以及安全系数进行进一步分析，利用正交分析法构建变形数学预测模型，利用改进的一次二阶矩法验算点法(AFORM)结合安全系数分析影响因素和可靠度之间的关系，从而综合评价系统的稳定性、可靠性。图 1所示为试验设计总流程图，此流程图主要介绍本研究主要过程和分析思路。

图1 试验设计流程图

1.1 影响因素的确定

经理论分析、现场观测并结合前人的研究成果发现，露天坑下空区破坏形式主要如下：1) 顶板两端剪切破坏，主要是空区跨度过大或坑底负载过大等因素导致变形破坏；2) 当顶板受到的拉应力大于岩石最大拉应力时出现的受拉破坏。两种破坏均会导致顶板的垮落和采空区的垮塌，给回采过程带来极大不便。铜绿山露天矿通过对坑底进行全尾胶结充填封底，相继进行干堆尾砂回填，尾砂源于尾矿的压滤并进行预脱水，同时减少了工业用水的使用。综合铜绿山矿回采实际，影响坑下采空区稳定性的主要因素如下。

1) 回填尾砂高度：尾砂回填范围为−185~15 m，共计 200 m，目前剩余180 m未回填，故后续研究价值很大；2) 境界顶柱高度：境界顶柱的高度并非越大越好，较大，矿体损失严重；较小，地下回采安全度受威胁，故在回采安全性与经济效益之间存在最优解，定义范围为8~34 m；3) 采空区跨度：2个相同跨度的平行采场沿矿体走向布置，跨度大小影响着空区稳定性变化，需满足采场布置范围的合理性；4) 采场间柱：为确保回采安全，采场之间预留宽度为的间柱，不仅影响稳定性，同时也和回采率关系重大。

对以上4个主要因素进行正交试验设计并加以研究。

1.2 可靠度理论研究

可靠度指标是评价是定性或定量地描述结构稳定性程度，即通过具体数值进行衡量和评价，利用非正态分布变量的一次二阶矩法验算点法(AFORM)进行安全系数与可靠度的综合研究，通过科学地定义并迭代加入验算点求解，其中验算点是可靠分析中的关键点。定义在假设变量因素服从正态分布或非正态分布前提下，导出可靠度解析式，最早是由Rackwitz和Fiessler(1978)[19]提出的一种当量正态转换法，亦称HL-RF算法或JC法。后由Roseenblatt完善至成熟，变换将相关的非正态随机变量变为独立标准正态分布，下为各影响因子可靠度指标与安全系数的关系计算步骤：

1) 令影响采空区稳定性的因子变量为，则有影响因子验算点为′，即变量x在验证点出，根据分布函数与概率密度函数相等原则等价变换为当量正态量x′，并确定x′的标准差与方差分别为、。按验算点上分布函数相同的前提，得到

可得

(2)

2) 按验算点在密度函数相等的条件

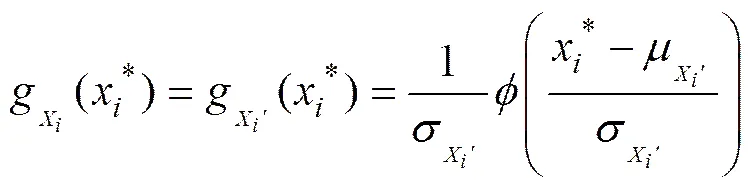
可得：

(5)

(6)

(7)

则有与满足式(9)，其中影响因子变量值X和转换后因子变量值X′均服从正态分布，则有

或表示为

(10)

建立可靠度与安全系数之间相互关系，分析露天坑干堆尾砂时地下空区稳定性，计算在不同参数模拟过程中，双空区顶板中心监测点的位移以及安全系数，通过建立的关系研究模拟的可靠性指标。

1.3 模型建立

基于FLAC3D数值软件建立的三维模型如图2所示，其中，模型尺寸为480 m×320 m×20 m，包含节点21300个，单元10520个。整个模型包含6部分，Ⅰ部分为露天坑回填尾砂，母岩成分主要为微风化大理岩、矽卡岩、闪长玢岩；Ⅱ部分为大理岩，节理较发育，岩芯成柱状；Ⅲ部分为斜长石岩，主要成分为方解石等，中厚层状构造，节理较发育；Ⅳ部分为矿体，节理一般发育，主要为铜铁矿，岩石比重较大；Ⅴ部分为矽卡岩，细粒结构，节理裂隙稍微发育，最大揭露厚度在18~60 m不等；Ⅵ部分为断层，强度较低，贯穿露天坑。对整个模型进行向约束，并对=0面进行全面约束，在两个空区顶板中心位置分别布置监测点1和点2，通过统计关键点竖向位移值、顶板周边区域塑性区面积、安全系数进行分析。

铜绿山矿岩体物理力学参数是根据室内岩石力学试验结果，并依据Hoek-Brown准则进一步处理，详见表1所示。

图2 矿体FLAC3D模型及空区开挖模型

表1 岩体物理力学参数

Tensile strength;—Cohesion;Dilatancy angle;—Internal friction angle;—Bulk modulus;—Shear modulus;—Density.

2 稳定性预测及可靠度分析

2.1 正交设计

若对4个影响因素下的所有情况进行逐一验证并模拟，工作量大且模拟过程盲目不具代表性。正交试验是在结合实际的基础上，选择均匀整齐的代表点作为重点研究对象，所得的结果对实际影响小。另外，正交水平需满足两个条件：1)每个因子在模拟试验中对应的水平数必须相同(均等性)；2)任意2因子在不同水平对应的模拟次数相同(正交性)。模拟过程中的指标即为影响空区稳定性的主要因素：尾砂回填高度()、空区跨度()、间柱宽度()、境界顶柱高()。每个因素()设置7个水平，正交试验方案选择L49(74)正交表，详见表2。

2.2 正交试验结果

49(74)试验表以表 2 确定的因子为基础，运用FLAC3D建立相关模型并后处理分析，为了获得试验条件下的目标值，共设计49次不同影响因素下双采空区稳定性的模拟方案，统计不同监测点的监测点位移、安全系数，得到正交试验结果如表3所列。

表3中下划线表示该数据对应的监测点位移达到一定的数量级，表明双空区顶板已发生破坏。相应的试验号为11、22、43、44、46、47；对应的竖向位移值为1834、2132、2415、3108、2563、2241 mm，空区顶板发生了垮塌破坏。试验中假设各因子间无交互影响，且指标间重要性比例相当，此时对敏感性分析影响最小。

表2 影响因子的水平值

表3 影响因子组合方案及模拟结果

为分析各影响因子对顶板稳定性的单独作用，定义表4中WS为在各水平值对应的第个因子的监测点位移、安全系数的平均值，另外为方便得到较准确的函数关系，定义破坏空区的位移值为 30 mm。

2.3 采空区变形分析

根据表4中反映的数据绘制各影响因子和监测点位移间的关系图(见图3)。通过回归分析拟合曲线中的函数关系，得到变量之间拟合相关程度较高的函数表达式如表5所列。

表4 模拟结果的分析计算表

图3 各因子与监测点位移及安全系数关系图

表5 各因子和位移的拟合结果

综合曲线关系图和拟合函数关系，得到

1) 顶板位移与尾砂堆高的关系

由图3(a)得，尾砂堆高和顶板位移呈非线性正相关，与安全系数呈负相关，较小时，顶板位移变化缓慢；随着的增大，变化速率明显增大，明显减小，且＞170 m时，速率最大，此时空区可能发生破坏，此时均值小于1，进一步尾砂堆积对空区稳定性的影响作用将变大。

2) 顶板位移与境界顶柱高度的关系

由图3(b)可得，空区监测点位移随着境界顶柱高度增加而减小，呈非线性减函数关系，但与呈线性增函数关系，平均变化速率为0.0267。表3模拟编号11空区发生破坏，可见较小时，较大，且变化率明显大于较大时的情况，此时均值较小，地下开采安全稳定性受到威胁。

3) 顶板位移与采空区跨度的关系

由图3(c)知，空区跨度和顶板中心位移呈非线性递增关系，与呈线性递减函数关系，平均变化率为−0.0329，地下模拟空区为双空区，比普通单空区复杂繁琐，对跨度表现尤其明显，其中与满足=0.01772−0.0191+9.0301；=5 m时，跨度小于采场空高(6 m)，顶板稳定性较好，位移量小；＞8 m＞采场空高时，位移变化平缓，采空区相对较稳定。的变化率随着值的增大明显变大，安全系数均值减小速率快，对地下空区稳定性影响较大。

4) 顶板位移与间柱宽度的关系

由图3(d)可得，顶板监测点竖向位移随着间柱宽度增加而减小，并与呈对数函数递增关系，＜5 m时，变化较急促，变化速率大。且由表3得，=2 m时，空区垮塌现象较多；＞5 m时，变化平缓，破坏发生现象少。经表 5 拟合得，与之间满足简单对数函数关系：=−6.031ln+19.993，与满足=0.2587ln+1.1139关系式，两者拟合程度较理想。

表5所列为各因子和位移的拟合结果。由表5可看出，各变量与的拟合相关系数2分别达到0.972、0.982、0.957、0.977；与的相关系数为0.952、0.981、0.973、0.991，拟合效果较好。

为综合分析4个影响因素与监测点位移的关系，在表5的基础上建立预测模型：

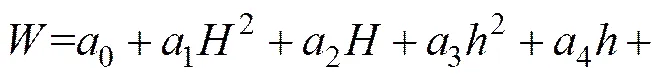
(10)

式中：0、1、2、…、7分别为该函数的待求系数，将正交试验表中数值代入函数，利用多元回归方程求解方程，则有

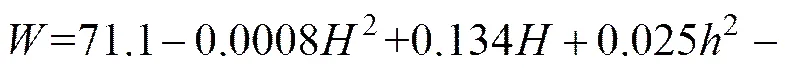
(11)

为研究变量影响空区稳定性的敏感度，统计49(74)试验表数值，并记录监测点位移极值，见表6。据统计，影响因素的敏感性分析结果为尾砂堆高、采场间柱宽度、双空区跨度、境界顶柱高度，满足敏感程度递减趋势。

表7所列为模拟过程中因子方差分析。由表7可看出，通过统计模拟过程中因子方差数据，并以该数据源求各变量平方和、自由度、均方、值、置信水平为95%的0.05值、影响因子对顶板稳定性的显著水平，得尾砂堆高和间柱宽度对空区稳定性影响较大，为主要因素；境界顶柱高度和空区跨度对其影响次之，四者均为影响空区稳定的重要因素。

表6 极差分析结果表

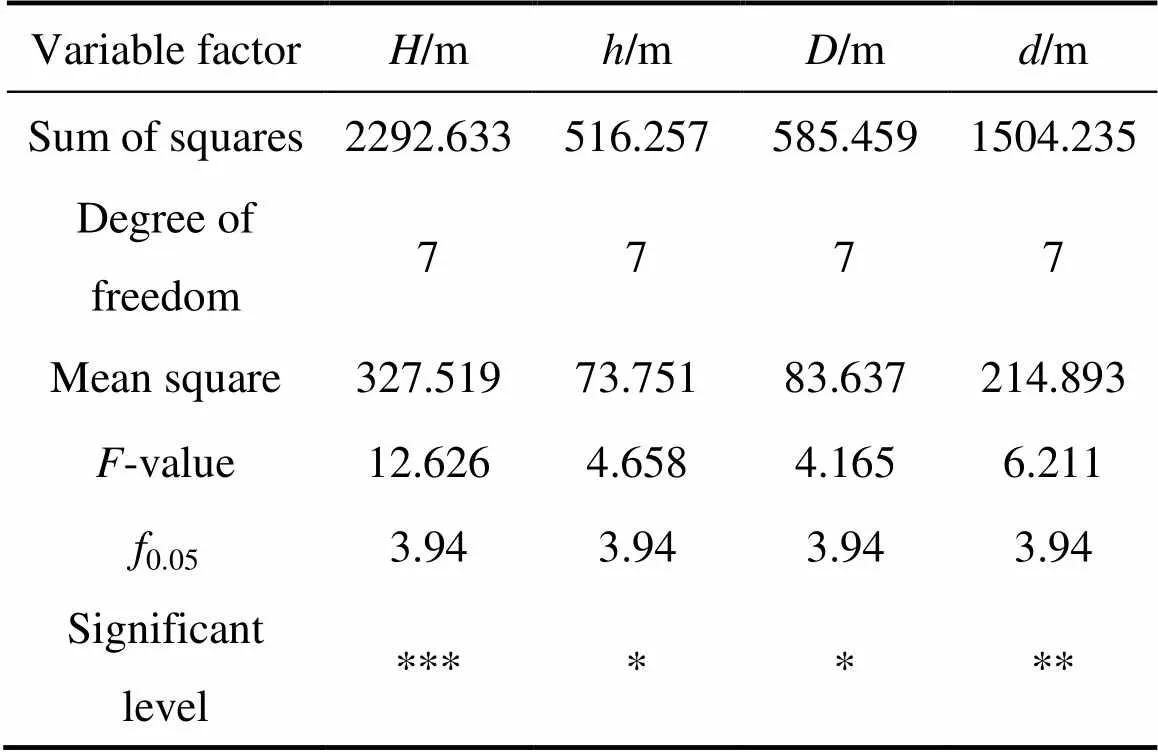
表7 方差分析表

2.4 可靠度分析

根据式(9)定义的可靠度与安全系数的相关关系，利用49次正交试验确定的模拟对4个不同影响因子进行关系计算，见图4，其中轴为安全系数，轴为顶板稳定性可靠度。由图4可知，4个因素两者的相关关系具有几个相同特征：1) 顶板稳定可靠度与安全系数均呈非线性正相关；2) 顶板可靠度随着安全系数的增大不会无限变大，而是收敛与某一固定值。然而亦有差别：1) 每个因素收敛的“峰值”大小不同，其中大小关系为＞＞＞；2) 不同安全系数对应的可靠度变化率均不相同，且前后增速有差别。

空区稳定性可靠度指标对不同影响因素的敏感度不同，敏感性排序为＞＞＞，即在相同安全系数条件下，不同因素对应的可靠度不同。当安全系数＜1.5时，两者线性关系比较明显，且拟合直线斜率差别不大；当安全系数1.7＞＞1.5时，两者关系越来越发散；＞1.7时，可靠度指标均达到小范围的变化区域，故可保持安全系数≈1.7，此时，可靠度和生产效益综合水平较高。

图4 不同影响因子下安全系数F和可靠度指标的相关关系

3 工程应用

铜绿山矿为高效回采南露天坑下I号矿体，在露天坑下沿走向布置两个平行采场83-04号和83-06号，应用中深孔2采1充方式回采，空区平均高度6 m，由于采场周边岩石破碎，节理较发育，故对顶板稳定性十分必要，由于模型只能将大致范围数值进行模拟计算，对于实际变动参数并不能准确地反映，故需通过拟合数学预测模型进行判断，表8所列为实测采场结构和周边参数，各参数值均为非整数。

表8 采场及周边参数值

通过代入建立的数学预测模型公式(11)得到预测位移=3.41 mm；另外，建立相关模型见图5左右空区分别为83-04和83-06号采场，其中图5(a)所示为采空区塑性区分布情况，间柱分布较多，顶板较少，由于东帮断层的存在，83-06号采场塑性区面积更大；图5(b)所示为位移矢量图，得到实际顶板位移=3.89 mm，两者相差0.48 mm，相对误差为12.3%，可以将预测值作为模拟结果。

图5 模拟采场的塑性区分布和位移矢量图

本文作者对铜绿山I号矿体下的83-04、83-06号顶板中心位移量分别进行了监测，测得两采场监测点位移值为3.34 mm、3.95 mm，同预测模型对比的误差分别为2.1%、13.6%，可作为实际的预测判断。利用建立模型得到安全系数为1.86，相应的可靠度为7.32，该试验采场可以安全回采。

4 结论

1) 通过正交试验设计，对影响露天转地下矿山复杂采空区稳定性的4个因素进行敏感性分析，结合极差分析结果得敏感度从高到低排序分别为：尾砂堆高、间柱宽度、空区跨度、境界顶柱厚度；通过方差分析得影响因子的显著程度为：＞＞＞，但结合置信区间0.05与值的对比可知，4个因子均为影响坑下采空区稳定性的重要因素，即都在评估稳定性生产过程中不可忽视。

2) 对正交试验模拟结果归类处理，利用多元回归处理法得位移与4个因素的相关关系预测函数，结合铜绿山试验采场进行参数代入、位移检验，结果显示该关系式的误差相对较小，对该矿体的回采安全性有一定的参考价值。

3) 将可靠度指标引用到地下复杂采空区稳定性安全评价中来，对4个不同影响因子的安全系数、可靠度关系进行统计计算。在参数相同情况下，4个因子的可靠度系数均收敛于某一值，且有＞＞＞，当＜1.5时，各因素近似呈线性关系；当1.7＞＞1.5时，两者关系发散；＞1.7时开始收敛于某一值。故=1.7时，可达到可靠度与安全生产效益的优化。

REFERENCES

[1] 何忠明, 曹平. 考虑应变软化的地下采场开挖变形稳定性分析[J]. 中南大学学报(自然科学版), 2008, 39(4): 641−646. HE Zhong-ming, CAO Ping. Deformation and stability analysis of underground stope after excavation considering strain softening[J]. Journal of Central South University (Science and Technology), 2008, 39(4): 641−646.

[2] 谢和平, 周宏伟, 王金安, 李隆忠, KWASNIEWSKI M A. FLAC在煤矿开采沉陷预测中的应用及对比分析[J]. 岩石力学与工程学报, 1999, 5(4): 397−401. XIE He-ping, ZHOU Hong-wei, WANG Ji-nan, LI Long-zhong, KWASNIEWSKI M A. Application and contrastive analysis of FLAC in forecasting coal mining subsidence[J]. China Mining Magazine, 1999, 5(4): 397−401.

[3] 张向东, 王 帅, 赵阳豪, 孙小彬. 基于端锚黏结式锚杆静、动载试验的非均匀受力锚杆单元[J]. 岩土力学, 2016, 37(1): 269−278. ZHANG Xiang-dong, WANG Shuai, ZHAO Yang-hao, SUN Xiao-bin. Non-uniform stress anchor element based on static and dynamic loading tests on bonded anchor bolt of end anchorage[J]. Rock and Soil Mechanics, 2016, 37(1): 269−278.

[4] Itasca Consulting Group. FLAC3D (Fast Lagrangian Analysis of Continua in 3 Dimensions) Version 3.1, Users Guide[R]. USA: Itasca Consulting Group, Inc., 2006.

[5] 胥孝川, 顾晓薇, 王 青, 刘剑平. 露天矿多采区受约束条件下全境界优化[J]. 东北大学学报(自然科学版), 2016, 37(1): 79−83, 93. XU Xiao-chuan, GU Xiao-wei, WANG Qing, LIU Jian-ping. Optimizing the whole boundary of open pit mining areas with restrictions[J]. Journal of Northeastern University (Natural Science), 2016, 37(1): 79−83, 93.

[6] 史秀志, 黄刚海, 张 舒, 周 健. 基于FLAC3D的复杂条件下露天转地下开采空区围岩变形及破坏特征[J]. 中南大学学报(自然科学版), 2011, 42(6): 1710−1718. SHI Xiu-zhi, HUANG Gang-hai, ZHANG Shu, ZHOU Jian. Goaf surrounding rock deformation and failure features using FLAC3Din underground mining shifted from open-pit in complex situation[J]. Journal of Central South University (Science and Technology), 2011, 42(6): 1710−1718.

[7] 张敏思, 朱万成, 侯召松, 郭孝庆. 空区顶板安全厚度和临界跨度确定的数值模拟[J]. 采矿与安全工程学报, 2012, 29(4): 543−548. ZHANG Min-si, ZHU Wan-cheng, HOU ZHAO-song, GUO Xiao-qing. Numerical simulation for determining the safe roof thickness and critical goaf span[J]. Journal of Mining & Safety Engineering, 2012, 29(4): 543−548.

[8] 邓清海, 曹家源, 张丽萍, 马凤山, 徐嘉谟. 转地下开采后龙首矿露天采坑底部隆起机理[J]. 采矿与安全工程学报, 2015, 32(4): 677−682. DENG Qing-hai, CAO Jia-yuan, ZHANG Li-ping, MA Feng-shan, XU Jia-mo. Uplift mechanism of the bottom of open pit after the transition from open-pit mining to underground mining in Longshou mine[J]. Journal of Mining & Safety Engineering, 2015, 32(4): 677−682.

[9] 赵延林, 吴启红, 王卫军, 万 文, 赵伏军. 基于突变理论的采空区重叠顶板稳定性强度折减法及应用[J]. 岩石力学与工程学报, 2010, 29(7): 1424−1434. ZHAO Yan-lin, WU Qi-hong, WANG Wen-jun, WAN Wen, ZHAO Fu-jun. Strength reduction method to study stability of goaf overlapping roof based on catastrophe theory[J]. Chinese Journal of Rock Mechanics, 2010, 29(7): 1424−1434.

[10] 吴启红, 彭振斌, 陈科平, 彭文祥, 陈乐求. 矿山采空区稳定性二级模糊综合评判[J]. 中南大学学报(自然科学版), 2010, 41(2): 661−667. WU Qi-hong, PENG Zhen-bin, CHEN Ke-ping, PENG Wen-xiang, CHEN Le-qiu. Synthetic judgment on two-stage fuzzy of stability of mine gob area[J]. Journal of Central South University (Science and Technology), 2010, 41(2): 661−667.

[11] 高 峰, 周科平, 胡建华, 邓红卫, 唐谷修. 充填体下矿体开采安全顶板厚度数学预测模型[J]. 岩土力学, 2008, 29(1): 177−181. GAO Feng, ZHOU Ke-ping, HU Jian-hua, DENG Hong-wei, TANG Gu-xiu. Mathematical forecasting model of safety thickness of roof for mining orebody under the complicated backfilling[J]. Rock and Soil Mechanics, 2008, 29(1): 177−181.

[12] 黄润秋, 刘卫华. 基于正交设计的滚石运动特征现场试验研究[J]. 岩石力学与工程学报, 2009, 28(5): 882−891. HUANG Run-qiu, LIU Wei-hua, In-situ test study of characteristics of rolling rock blocks based on orthogonal design[J]. Chinese Journal of Rock Mechanics, 2010, 28(5): 882−891.

[13] 吴顺川, 高永涛, 杨占峰. 基于正交试验的露天矿高陡边坡落石随机预测[J]. 岩石力学与工程学报, 2006, 25(1): 2826−2832. WU Shun-chuan, GAO Yong-tao, YANG Zhan-feng, Random prediction of rock fall of open-pit mine high-steep slope based on orthogonal experiment[J]. Chinese Journal of Rock Mechanics, 2006, 25(1): 2826−2832.

[14] 付宏渊, 刘建华, 张 立, 吕东滨. 基于正交试验的岩质边坡动力稳定性分析[J]. 中南大学学报(自然科学版), 2011, 42(9): 2853−2859. FU Hong-yuan, LIU Jian-hua, ZHANG Li, LÜ Dong-bin. Dynamic stability analysis for rock slope based on orthogonal test[J]. Journal of Central South University (Science and Technology), 2011, 42(9): 2853−2859.

[15] LEBRUN R, DUTFOY A. An innovating analysis of the Nataf transformation from the copula viewpoint[J]. Probabilistic Engineering Mechanics, 2009, 24(3): 312−320.

[16] 李典庆, 蒋水华, 周创兵, 方国光. 考虑参数空间变异性的边坡可靠度分析非侵入式随机有限元法[J]. 岩土工程学报, 2013, 35(8): 1413−1422. LI Dian-qing, JIANG Shui-hua, ZHOU Chuang-bing, FANG Guo-guang. Reliability analysis of slopes considering spatial variability of soil parameters using non-intrusive stochastic finite element method[J]. Chinese Journal of Rock Mechanics, 2013, 35(8): 1413−1422.

[17] LEBRUN R, DUTFOY A. Do Rosenblatt and Nataf is probabilistic transformations really differ [J]. Probabilistic Engineering Mechanics, 2009, 24(4): 577−584.

[18] 王玉杰, 徐佳成, 汪小刚, 曾庆义. 基于可靠度分析的锚杆抗拔安全系数取值标准研究[J]. 岩土工程学报, 2012, 34(2): 303−308. WANG Yu-jie, XU Jia-cheng, WANG Xiao-gang, ZENG Qing-yi. Criteria for determining factor of safety of anchor against pull-out by using reliability analysis[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(2): 303−308.

[19] DUTFOY A, LEBRUN R. Practical approach to dependence modelling using copulas [J]. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, 2009, 223(4): 347−361.

(编辑 李艳红)

Deformation prediction and reliability analysis of underground mining shifted from open-pit based on orthogonal experiment

CHEN Jia-yao, SHI Xiu-zhi, ZHOU Jian, QIU Xian-yang

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

The stability of underground mined-out area is the key technology for Tong-lü-shan underground mining shifted from open-pit of safely and efficiently stoping residual ore was analyzed. The orthogonal experiment and simulation software FLAC3D based on four influence factors including column thickness (), gob area span (), roof thickness () and height of tailing gangue () were estimated. The test results of 49 groups were analyzed by the means of range, variance and regression analysis, meanwhile using factor of safety and reliability index to assess the safety and efficiency of the recovery. The results indicate that the degree of fit between 4 factors and displacement () or safety factor () is good, and the correlation coefficient (R) is more than 0.952. A mathematical forecasting model of displacement under 4 factors is obtained, which is proved effectively during the engineering practice. The significant degree of influence on the stability of mined out area during the 4 factors meets the relationship of＞＞＞. The importance degree ranking meets＞＞＞by the comparison of confidence interval0.05and, all of these 4 factors can’t be ignored. The optimal degree of safety and reliability can be reached when safety factor is more than 1.7 and the reliability index begins to converge.

orthogonal experiment; reliability index; numerical simulation; tailings discharge into open-pit; boundary pillar

Projects(2013BAB02B05) supported by the “Twelve-Five” National Science and Technology Support Program of China; Project(2015CX005) supported by the Innovation Driven Plan of Central South University, China

2015-11-23; Accepted date:2016-04-19

SHI Xiu-zhi; Tel: +86-13974801752; E-mail: shixiuzhi@263.net

1004-0609(2016)-11-2383-10

TD 325

A

国家“十二五”科技支撑计划资助项目(2013BAB02B05)；中南大学“创新驱动计划”项目资助(2015CX005)

2015-11-23；

2016-04-19

史秀志，教授，博士；电话：13974801752；E-mail：csublasting@163.com