舰船致生物受激发光的水中传输特性研究*

张显峰 曹 静 宗思光 吴荣华 梁善永

(海军工程大学电子工程学院 武汉 430033)



舰船致生物受激发光的水中传输特性研究*

张显峰 曹 静 宗思光 吴荣华 梁善永

(海军工程大学电子工程学院 武汉 430033)

根据光子能量的计算方法，计算分析了海洋中生物体的发光能力，结果表明在低浓度分布时发光生物体的辐照度是完全可测的；考虑随机介质中光传输的多次散射，利用蒙特卡罗方法建立了研究生物光传输特性的理论模型和算法，仿真计算结果表明：生物光在均匀介质中的传输符合朗伯特-比尔衰减定律，随着距离的增加传输能量按指数衰减；通过对给定模型参数的计算表明472nm的生物光在一类海水中传输120m后仍然能够被高灵敏的探测器探测到；波长对生物光水中传输的整体特性影响不大，但随着波长的增加衰减系数增大；生物的粒径大小对衰减系数的影响较大，随着粒径的增大光传输的衰减系数会有较明显的增大。

生物受激发光; 传输特性; 蒙特卡罗; 腰鞭毛虫

Class Number O482.31

1 引言

生物受激发光是海洋生物体受流场刺激而产生的发光现象，通常可在破碎的波浪[1]、舰船的尾流[2]、运动生物[3]的海域等情况下观测到。生物受激发光的研究可为水下目标探测提供一种新的技术手段具有广阔的应用前景，可应用在舰艇尾迹遥感、反潜作战、近海岸反蛙人预警等军事领域，也可应用在海洋水质监测、海洋搜救、鱼群探测、海洋初级生产力监测等方面。由前期的研究[4]可知腰鞭毛虫在机械刺激下能够发出闪烁的且人眼清晰可见的光，那么海洋中这类生物体的发光能力如何？这类光的水中传输情况如何？能否对其进行远距离探测？本文在分析海洋中生物体的发光能力基础上，通过数值计算的方法对生物光的传输进行模拟，分析研究生物光的水中传输特性，从而可为今后生物受激发光的水中探测技术研究提供一定的理论基础。

2 海洋中生物体的发光能力计算

发达国家特别是美国已经在其近海岸布置了大量的光学传感器[5]，全天候实时对沿岸海域中的发光能力进行测量，研究海洋生物发光的季节变化、区域变化等特性；另外他们研制的发光测量浮筒BioBuoy等装置[5]可对大洋中的生物发光能力进行测量。根据已有资料中的测量结果，下面计算一下海洋中单位体积内的生物发光能力。

根据爱因斯坦的光量子假设，光子的能量q与频率ν和相应波长λ的关系为

q=hν=hc/λ

(1)

其中真空光速c=2.998×108m/s，普朗克常数h=6.626×10-34J·s。则波长λ为472nm的一个光子的能量为

e=6.626×10-34×2.998×108/472×10-9

≈4.209×10-19J

(2)

学者Lynch[6]研究了每秒钟被扰动生物体的发射光子数量，其中发光细菌为104光子s-1·cell-1，腰鞭毛虫为109～1011光子s-1·cell-1。假设海水中生物体腰鞭毛虫的浓度ρ为低浓度时的2000cell/m3，而单个细胞每秒的发光量P取5×1010个光子，且它们发光的平均波长为472nm。则单位体积内生物体的发光强度为

I=ρ·P·e

=2000×5×1010×4.209×10-19

≈4.2×10-5W/m3

(3)

如果这个能量产生于一个体积为1m3的单独球体中，那么这个球体的表面就会接收到一个量级为10-5W/m2的辐照度。表1给出了不同条件下海洋表面的可见光福照度情况，与表中的数据比较可知，低浓度时生物受激发光的辐照度大于一个满天繁星而且没有云的夜晚的辐照度，小于一个有月光的明亮之夜的辐照度。同样的，当生物体浓度增大到106cell/m3的中等浓度量级时，那么就会在海面产生量级为10-3W/m2的辐照度，此时的辐照度就会大于洁净大气中有月光情况下的辐照度，因此海洋中的生物发光是完全可测的。此外，Rohr等通过海上实验和理论分析也证实了在近海岸海域采用多光谱分析技术几乎能够探测到夜间任何时刻的受激生物光尾流[7]。

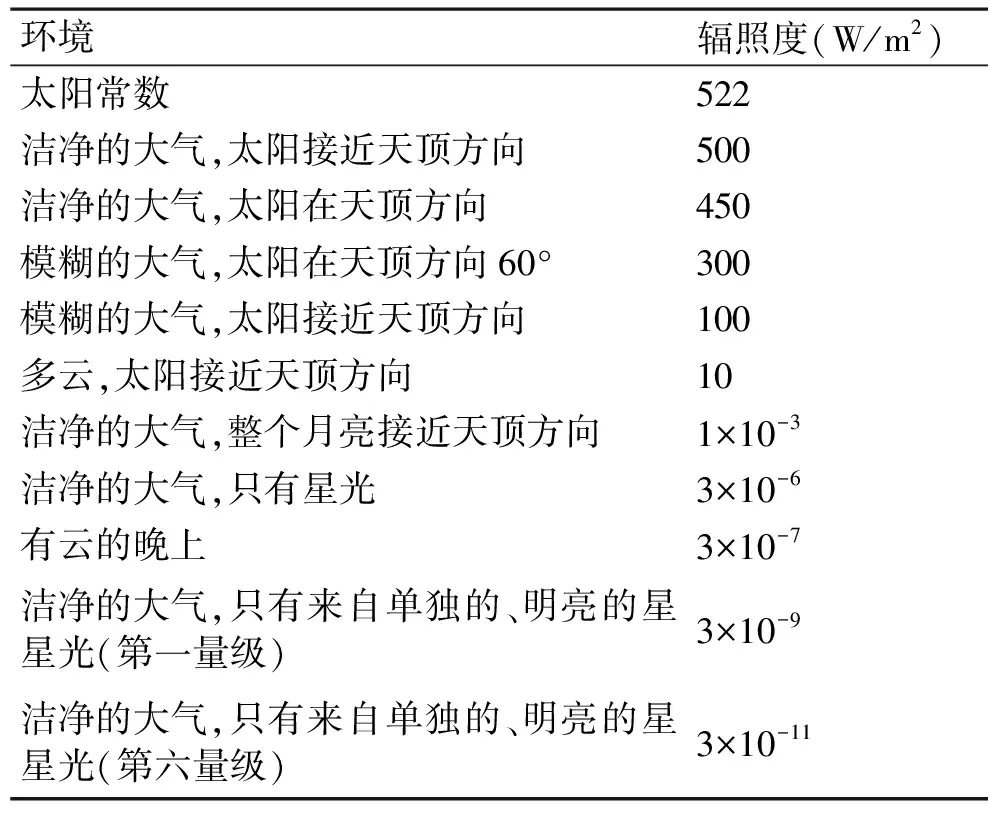
表1 海洋表面可见光波长范围(400nm～700nm)具有代表性的总辐照度(直射部分加上辐射部分)

3 生物光水中传输的分析方法

3.1 蒙特卡罗方法概述

蒙特卡罗(Monte Carlo)方法，是一种利用重复的统计试验来求解物理和数学问题的方法，又称为随机抽样或统计试验方法，属于计算数学的一个分支。在光学仿真中使用最多的是基于蒙特卡罗方法的光子跟踪法,目标是获得不同条件下的光子接收信号，从而进行信号分析。从原理上来讲，要了解一个光子在静态介质中的运动状态，只需要知道两个基本条件，光子的运动路程和光子的运动方向，光子在运动过程中会与介质微粒发生相互作用(一种常用的叫法称为“碰撞”)，蒙特卡罗模型所需满足的一些基本假设为

1) 一个光子与介质微粒发生的相邻两次碰撞之间存在一个自由运动过程，且可以认为作匀速直线运动；

2) 光子与介质或微粒相互作用只在碰撞点发生，即光子与介质或微粒只发生碰撞(包括吸收和散射过程)；

3) 在入射光束范围内可把入射光看作平面波，即在入射光束截面上的光子数分布是均匀的。

3.2 光传输特性蒙特卡罗模拟的步骤

蒙特卡罗方法求解光子传输问题的一般过程包括：光子源分布抽样、碰撞过程计算、光子终止判断和统计处理等，其流程图如图1所示。

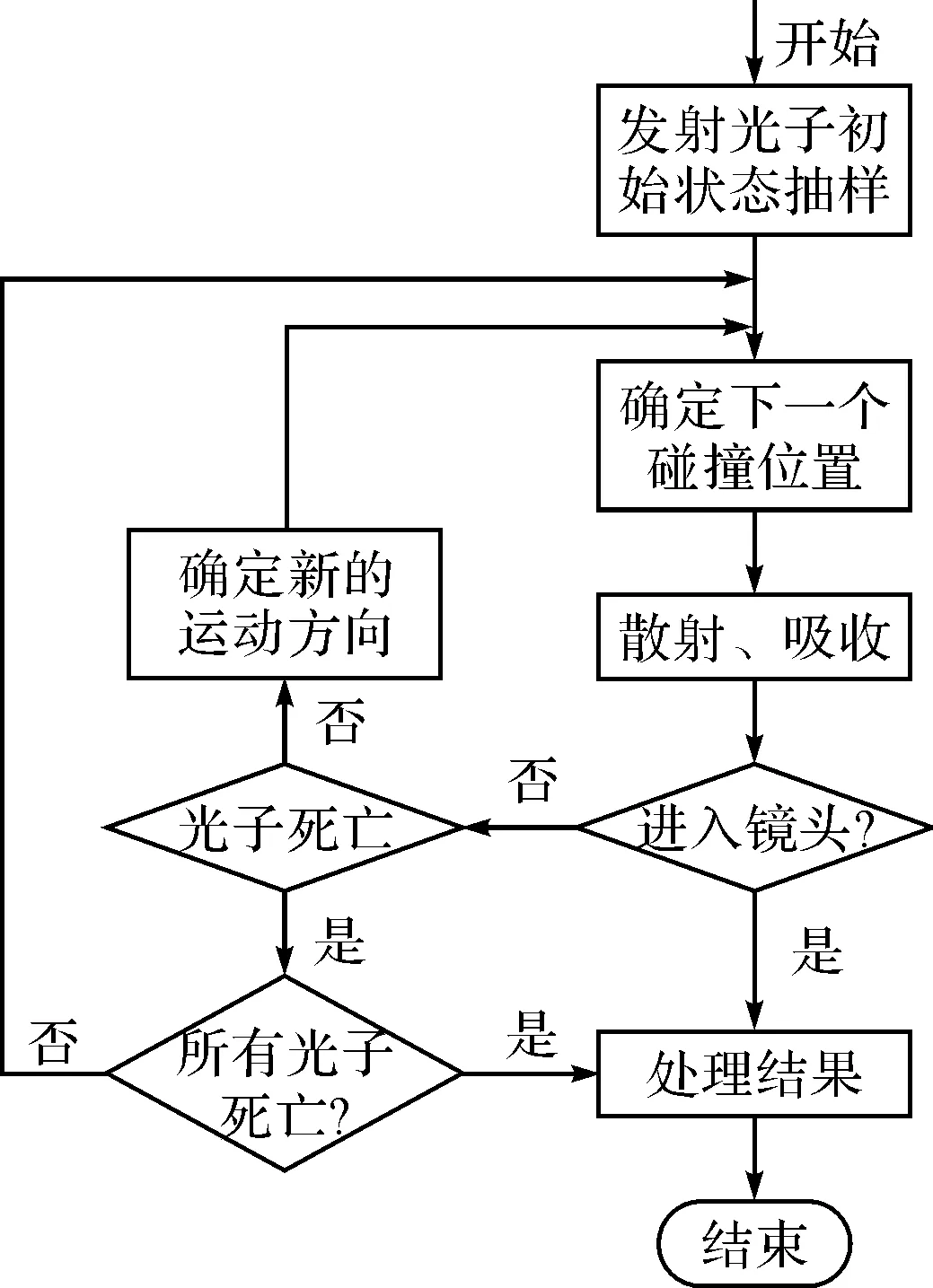
图1 光子运动模拟的流程图

1) 确定光子行步长[8]

在位置L处经过散射的一个光子的生存概率为

W=exp(-μL)

(4)

其中μ表示介质的衰减系数，由此可得，光子在两次碰撞间距离L的抽样函数为

L=-lnξ/μ

(5)

其中，ξ为(0，1)之间的随机数。于是，第m+1个碰撞点的位置可表示为[8]

(6)

式中，(Um+1，Vm+1，Wm+1)为光子运动的方向余弦。

2) 确定散射碰撞后光子的运动方向

光子碰撞后发生散射，运动方向改变，设第m次碰撞后光子的散射角为θm，方位角为φm，通过坐标变换可得光子碰撞后新的方向余弦为[8]

+Umcosθm

(7)

如果光子的运动方向接近z轴方向，则新的方向余弦为[8]

(8)

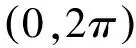
φm=2πξ

(9)

式中ξ表示(0，1)之间均匀分布的随机数。

3) 光子的碰撞与吸收

利用Poole[10]等提出的统计加权的方法，在计算中给每个光子赋一个初值为ω0=1的权值，当光子在介质中发生碰撞时，权值减少。此时第m次碰撞后的权值ωm为

ωm=ωm-1ωs

(10)

式中ωm-1是碰撞前的权值；ωs是单次散射率。应用加权技术的目的是为了提高计算效率。在计算中，认为吸收发生在散射点之间。

4) 判断光子是否进入接收系统镜头

判断过程分为两步：首先由光子状态参数zm和zm+1判断光子是否有可能进入镜头，接着由光子打在镜头所在平面上的位置判断其是否进入镜头。

5) 记录接收光子

若光子在第m次碰撞后经过一段自由运动距离打在镜头上，则记录为接收信号中的一个光子，并对光子状态矩阵的第m+1列光子状态进行向量赋值。

4 仿真结果及分析

基于米氏散射理论的传统蒙特卡罗光传输模拟均是对球形粒子进行计算的，而大部分生物体都是非球形，因此首先要将生物体等效成球形粒子。表2给出了几种典型发光生物体的尺寸参数和模拟中使用的光学参数。在模拟过程中，设定初始光子数目为106个，探测器镜头半径为0.05m，海水的折射率为1.34，其他参数根据具体情况的不同而改变。

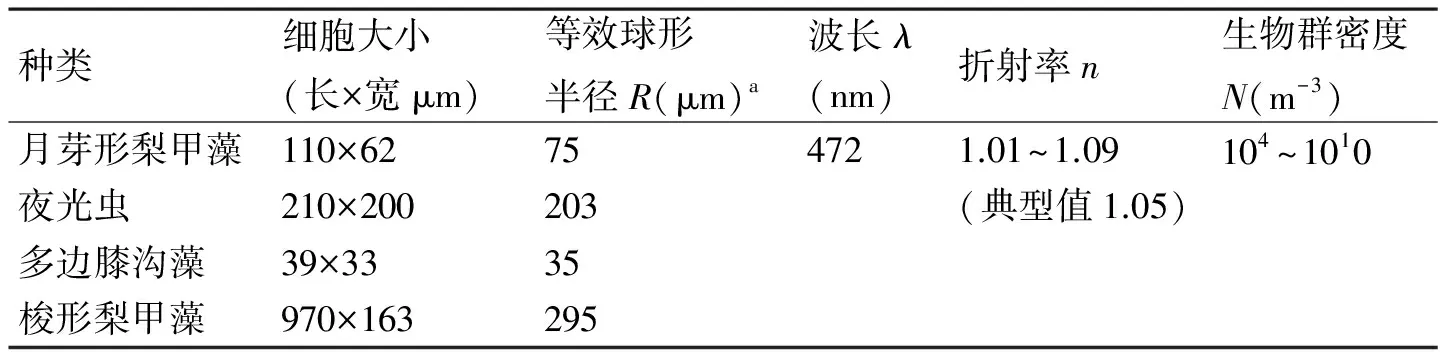
表2 几种腰鞭毛虫的典型参数

4.1 生物受激发光的传输特性分析

图2给出了R=35μm、λ=472nm、N=106情况下生物光分别传输1m、10m、60m、120m的时间特性，其中横坐标为接收的时间，单位为ns，纵坐标为相对光强即接收到的权值光子数与总光子数的比值。从图中可以看出不同距离上的光传输具有相似的时间特性，光信号在微小的时延后出现明显的波峰随后光子数急剧下降，也就是说能够到达接收器的光子几乎都是同时到达的，这主要是由于模拟中光的前向传输非常强，即使是碰撞次数很多的光子，也都能够以近似等于直线距离的光程到达接收器。同时随着距离的增大，能够接收到的光子数急剧下降，光子要经过更多次的散射过程才能透过粒子介质层，而次数很大的散射过程发生概率较小，所以就如同显示结果一样，光子要么以最快的速度到达接收器，要么就会被介质吸收或散射永远到达不了接收器。

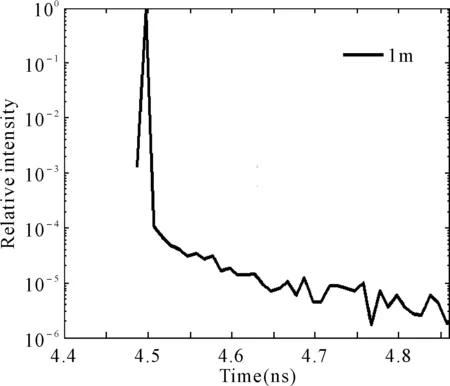
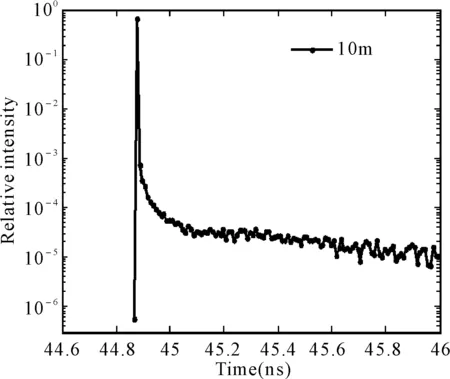
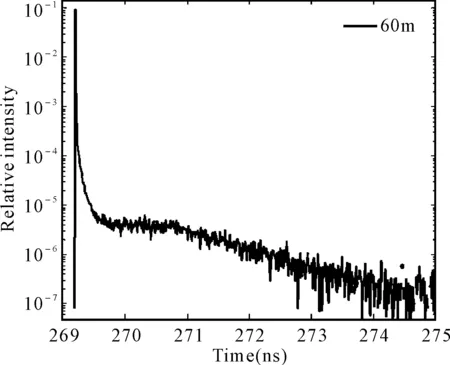
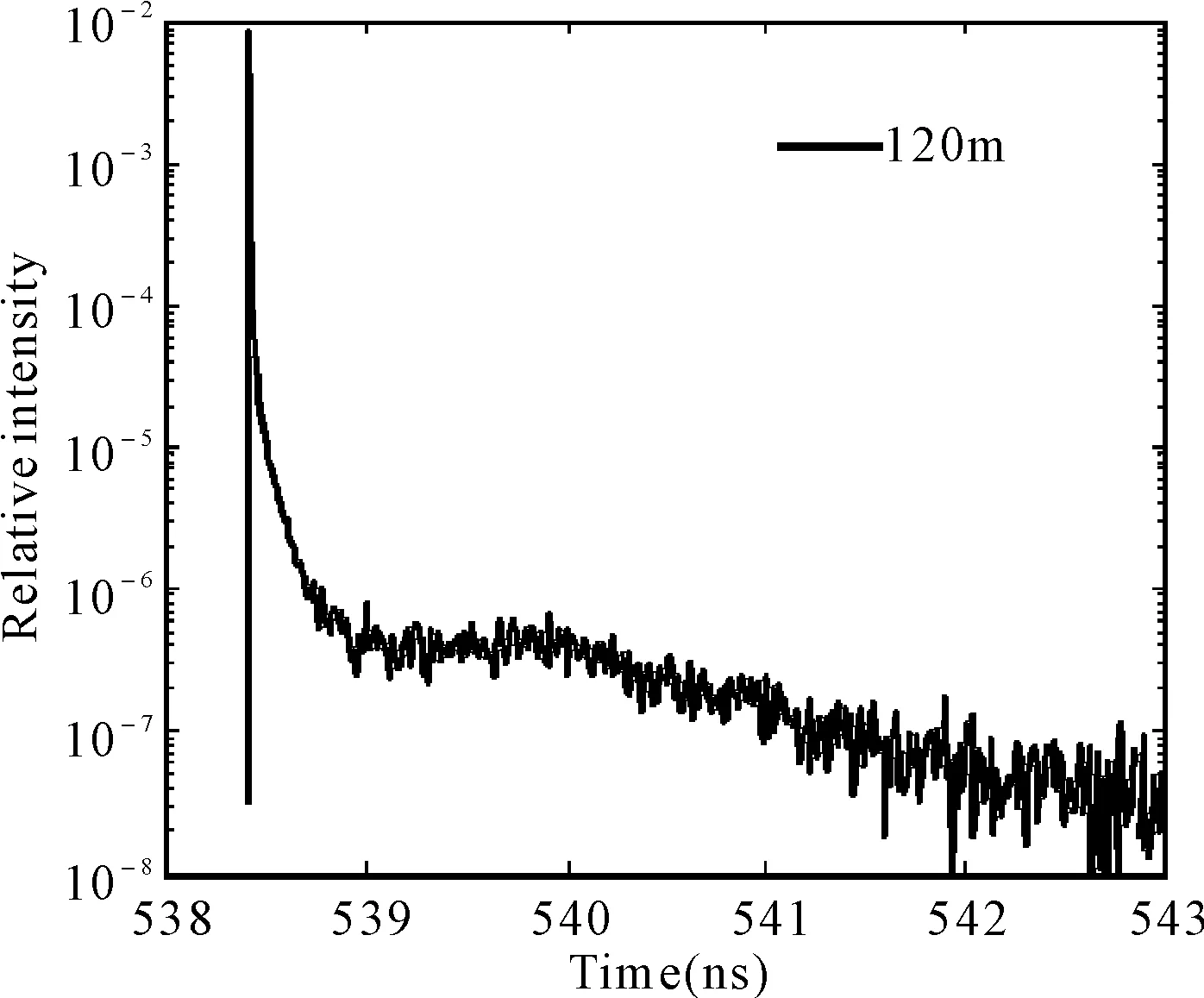
图2 不同距离上生物受激发光的传输特性

生物光传输不同距离下的峰值光子数如图3所示，横坐标为光传输的距离，纵坐标为接收到的光子数。从图中可以看出随着距离的增加，光子能量以长度的函数为参数按指数衰减，符合朗伯特-比尔衰减定律的传输特性。另外，图中给出了当衰减系数为0.0433m-1时朗伯特-比尔定律的理论曲线，比较两条曲线可知，模拟结果与理论计算值吻合，因此可以认为在此参数下介质的衰减系数为0.0433m-1。根据Smith和Baker的研究[11]表明纯海水在光波长470nm时的衰减系数为0.0193m-1，将模拟所得的衰减系数0.0433m-1代入衰减系数与叶绿素浓度的经验公式[11]可得生物体的叶绿素浓度约为0.0073mg/m3。而又根据1998年Morel的研究可知[12]，叶绿素浓度为0.01mg/m3的均匀一类水体的透光深度约为153m，这与模拟结果中的160m距离处仍有1‰左右的初始光透过相吻合。另外，1981年Losee和Lapota对生物光传输的测量结果表明[13]，在传输114m后生物光的测量值仅仅衰减了22%，但是考虑到生物光的微弱性，生物光的远距离传输也是不现实的，综合考虑模拟结果和目前所掌握的国内外资料，认为生物光在清澈的一类海水海域传输120m的距离后高灵敏的探测器还能够感知到。

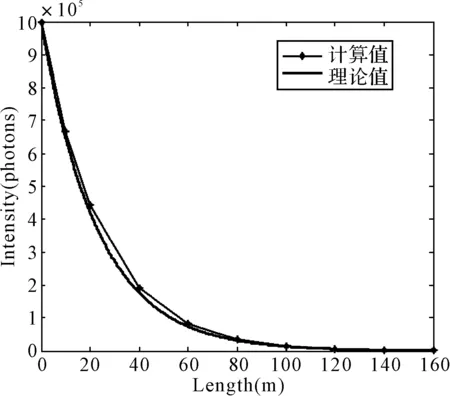
图3 生物光传输的距离衰减特性

4.2 不同波长对传输信号的影响

据Widder对海洋中70多种主要发光生物体的研究表明，生物光的波长主要集中在450nm～580nm，图4在半对数坐标系中给出了波长λ=450nm、λ=472nm、λ=533nm、λ=574nm时的光传输特性。模拟条件：光子数106个、采样率为10-9、FOV=50mrad、生物体半径R=35μm、N=106m-3。从图中可以看出，传输信号按照指数规律随距离衰减，生物光波长的变化对传输信号的影响不大。但是随着波长的增加，光衰减越来越严重。也就是说在同一种介质中，随着生物光波长的增加，介质的光衰减系数增大，这一特点与文献[11]中给出的纯海水的光衰减特性是一致的。

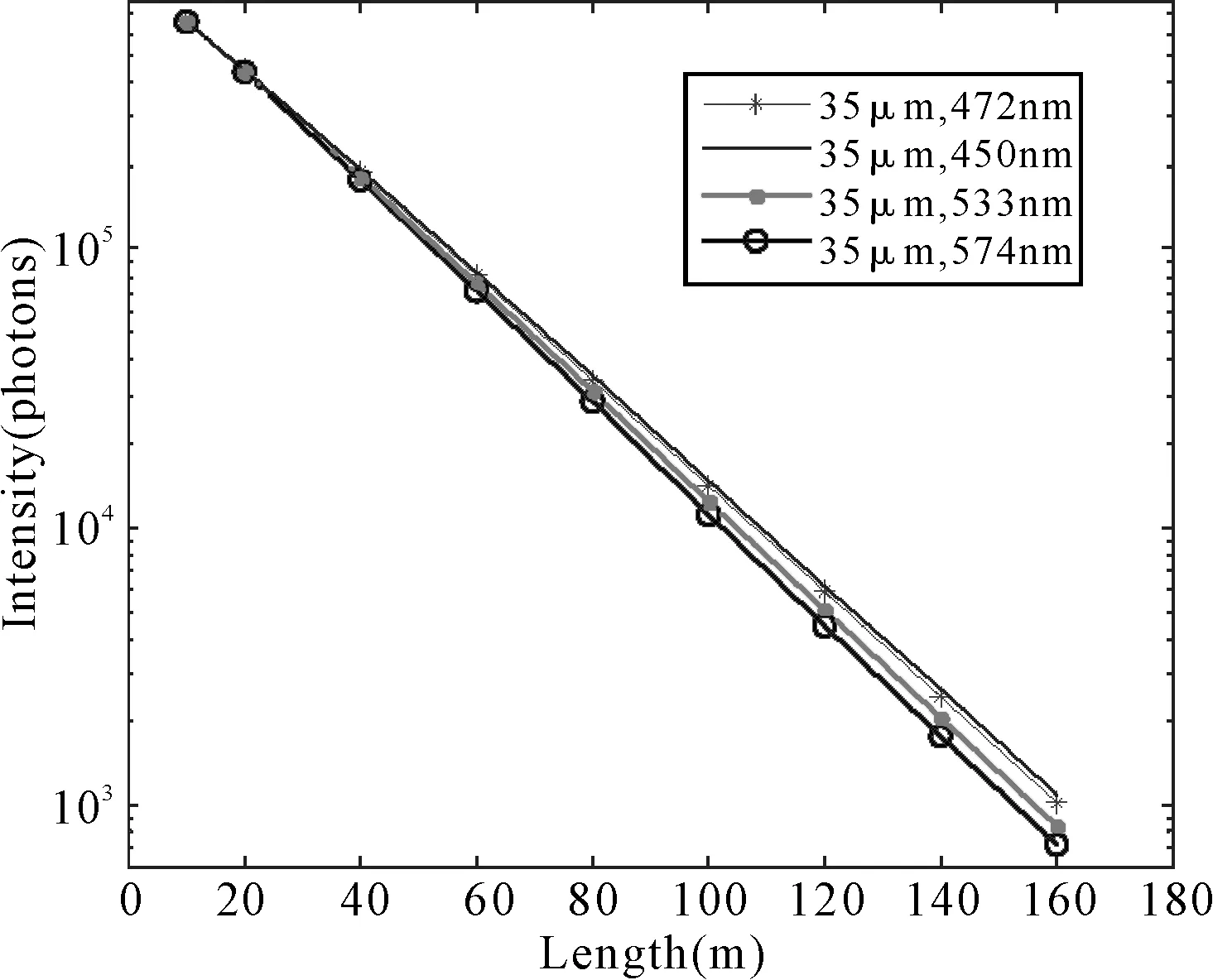
图4 不同波长的生物光传输特性

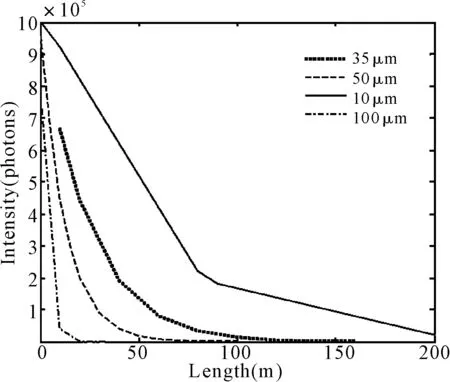
图5 生物体粒径不同时对生物光传输的影响

4.3 不同粒径对传输信号的影响

如图5所示，计算了海水中生物体的平均半径R分别为10μm、35μm、50μm、100μm时对光传输的影响，其中模拟光子数目106个、采样率为10-9、FOV=50mrad、生物体密度N=108m-3。从图中可以看出，粒径的大小不能改变光传输的基本特性，所有生物发光随着距离的增加按指数衰减。但在其他条件一致的情况下，粒径的大小对整个介质的衰减系数影响较大，粒径越小，衰减就越小，传输的距离就越远；这主要是由于模拟中设置的生物体浓度已相对较大，当单个生物体的半径增大时就会使光子的碰撞概率增大，从而增加了光子被散射和吸收的概率，使向前传输的可能性变小，甚至有些光子还会发生后向散射；如果无限制增大粒子半径，那么等同于光子在水中碰到大物体，则此时的所有光子将会被反射回来。所以，在其它条件不变的情况下，生物体粒径增大将会使光传输距离缩短。

5 结语

根据光子能量的计算方法，结合海洋中实际的生物体分布浓度和单个生物体平均发光强度，计算分析了海洋中生物体的发光能力，并与国外已有的辐照度测量数据进行了对比，结果表明在低浓度分布时发光生物体的辐照度是完全可测的。利用蒙特卡罗方法模拟生物光在含有大量均匀分布生物体的海水随机介质中传输过程及模型，采用该模型对传输信号进行了模拟，并在此基础上分析了不同参数对光传输的影响，结果表明：生物光在均匀介质中的传输符合朗伯特-比尔衰减定律，随着距离的增加传输能量按指数衰减；波长对生物光传输的整体特性影响不大，但随着波长的增加衰减系数增大；生物体的粒径大小对衰减系数的影响较大，随着粒径的增大光传输的衰减系数会有较明显的增大。

[1] Stokes M D, Deane G B, Latz M I, et al. Bioluminescence imaging of wave-induced turbulence[J]. J. Geophys. Res.,2004,109,C01004.

[2] Rohr J, Hyman M, Fallon S, Latz M I. Bioluminescence flow visualization in the ocean：an initial strategy based on laboratory experiments[J]. Deep-Sea Res,2002,49:2009-2033.

[3] Rohr J, Latz M I, Fallon S, et al. Experimental approaches towards interpreting dolphin-stimulated bioluminescence [J]. J. Exp. Biol.,1998,201:1447-1460.

[4] 曹静,吴荣华,马治国,等.生物受激发光的管流实验研究[J].发光学报，2013,34(10):1332-1338.

[5] Lapota D.Night time surveillance of harbors and coastal areas using bioluminescence camera and buoy systems[J].Proceedings of SPIE，2005，5780：128-137.

[6] Lynch D K，Livingston W.Color and Light in Nature[M].Cambridge：University Press,1995.

[7] Rohr J, Schoonmaker J, Losee J, et al. Flow visualization in the ocean-implications of laboratory bioluminescence experiments[C]//OCEANS’99 MTS/IEEE, Riding the Crest into the 21st Century,1999(1):145-156.

[8] Makoto I，Kazuhiro G，Takashi O，et al.Simulation of spectral reflectance of multiple scattering medium using the Mie theory combined with the Monte Carlo method[J].SPIE，2003，4955：305-313.

[9] Michael R S.Laser-light scattering from polar ice theory and experiment[D].New Yok： State University of New York，2004.

[10] Poole L R，Venable D D，Campbell J W.Sernianalytic Monte Carlo radiative transfer model for oceanographic lidar systems[J].Applied Optics，1981，20：3653-3656.

[11] Mobley C D.Light and water：radiative transfer in natural waters[M].San Diego：Academic Press，1994.

[12] Bricaud A，Morel A，Babin M，et al.Variations of light absorption by suspended particles with chlorophyll a concentrations in oceanic (Case 1) waters：analysis and implications for bio-optical models[J].J. Geophys. Res.,1998,103：31033-31044.

[13] Losee J，Lapota D.Bioluminescence measurements in the Atlantic and Pacific [C]//In Bioluminescence Current Perspectives (ed. K H Nealson).Minneapolis：Burgess Publishing，1981：143-152.

Transmission Characteristics of Stimulated Bioluminescence By Ship

ZHANG Xianfeng CAO Jing ZONG Siguang WU Ronghua LIANG Shanyong

(College of Electronic Engineering, Naval University of Engineering, Wuhan 430033)

The luminescent capability of organisms in sea water was calculated and analyzed based on the calculation method of photonic energy combined with the actual concentration and bioluminescent intensity of organisms in the ocean. The results showed that the radiometric illumination with low concentration of bioluminescent organisms was detectable. The theory models studying the transmission characteristics of bioluminescence were developed using Monte-Carlo method and the Monte-Carlo simulation algorithm calculating multi-scattering of oceanic bioluminescence was established considering of the multi-scattering effects of transmission in random medium. The transmission signals of bioluminescence were simulated with above algorithm. The results showed that the transmission of bioluminescence in the sea water was met with the Lambert-Beer law, with development of distance the energy was reduced by index. According to the simulation, the bioluminescence with 472nm would be detected by high sensitive detection when it transmitted 120 meters. And the transmission didn’t depend on the bioluminescence wavelength, the attenuation coefficient would be increased with the wavelength. The attenuation coefficient seriously depended on the bioluminescence organism size, with the development of size the attenuation of bioluminescence transmission would be obviously increased.

stimulated bioluminescence, transmission characteristics, Monte-Carlo, dinaflagellate

2016年5月14日,

2016年6月26日

海军工程大学自然科学基金(编号：HGDQNJJ15012)；海洋工程国家重点实验室(上海交通大学)开放课题项目(编号:1207)；国家自然科学基金(编号：41406047)资助。

张显峰,男，硕士，讲师，研究方向：尾流场中的光学特性以及光电技术应用。曹静，女，博士，讲师，研究方向：光电技术应用以及光电对抗。

O482.31

10.3969/j.issn.1672-9730.2016.11.036