毫米波多通道接收组件隔离度对移相的影响

武红玉，厉志强，乔明昌，赵子润

(中国电子科技集团公司第13研究所，石家庄 050051)



毫米波多通道接收组件隔离度对移相的影响

武红玉，厉志强，乔明昌，赵子润

(中国电子科技集团公司第13研究所，石家庄 050051)

介绍了多通道接收组件的典型原理框图，给出了通道隔离度、耦合度、移相精度和移相寄生调幅的概念，使用相量法推导了通道耦合度对移相精度和移相寄生调幅影响的计算公式，指出理论上隔离度对移相指标的影响与频率无关。利用软件仿真了通道隔离度对移相精度和移相寄生调幅的影响，得到了与公式计算相同的数值，两者互相得到了验证。提出了改善通道隔离度的方法，设计加工了一种Ka波段的四通道接收组件，改善了通道隔离度，具有较好的移相精度和移相寄生调幅指标。

毫米波；多通道；隔离度；移相精度；移相寄生调幅

0 引 言

毫米波雷达作为现代雷达技术发展的重要方向，它的优点是可以实现大范围、快速、多目标的搜索和跟踪，重量小，体积轻、抗干扰能力强[1-2]。毫米波多通道收发组件是毫米波雷达的核心部件，近年来，随着单片微波集成电路(MMIC)和微封装工艺的快速发展，毫米波收发组件发展迅速，体积也越来越小。2010年Jia-Chi Samuel等人[3]报道了一种Ka波段8通道接收电路，它基于多层液晶高分子(LCP)工艺，每个通道集成1片低噪声放大器(LNA) MMIC和1片5位移相器MMIC， 重量仅为12.3 g；2012年Young-bae Jung[4]报道了一种K波段四通道接收电路，每个通道集成2片LNA MMIC、1片5位移相器MMIC以及滤波器，组件参考态增益≥24 dB，全部移相态最大移相误差±11.25°；国内2015年报道了一种Ka波段16通道组件[5]，它基于多层电路板工艺，每个通道集成一片6位移相器MMIC，线性增益≥25 dB，移相均方根误差(RMS)≤5°。

毫米波多通道接收电路设计的难点之一是由于通道之间的间距小、腔体深度低(以Ka波段为例，间距5 mm左右，腔深1.5 mm左右)，同时毫米波频段辐射增强，导致通道间耦合增强，隔离度变差，信号在通道间串扰，从而对移相精度和移相寄生调幅等指标产生影响，使其变差。

本文系统地研究了多通道接收组件的通道耦合度对移相精度、移相寄生调幅指标的影响。文章先从多通道接收组件的原理框图出发，一方面分析了移相指标变差的原因，利用数学推导得到了计算公式，给出了典型数值；另一方面在ADS下进行了仿真，仿真结果和数学公式计算的结果完全吻合。

1 多通道接收组件原理

两通道接收组件的典型原理框图如图1所示，它由两部分组成：一部分是通道内部分，另一部分是功分器和驱动放大器。

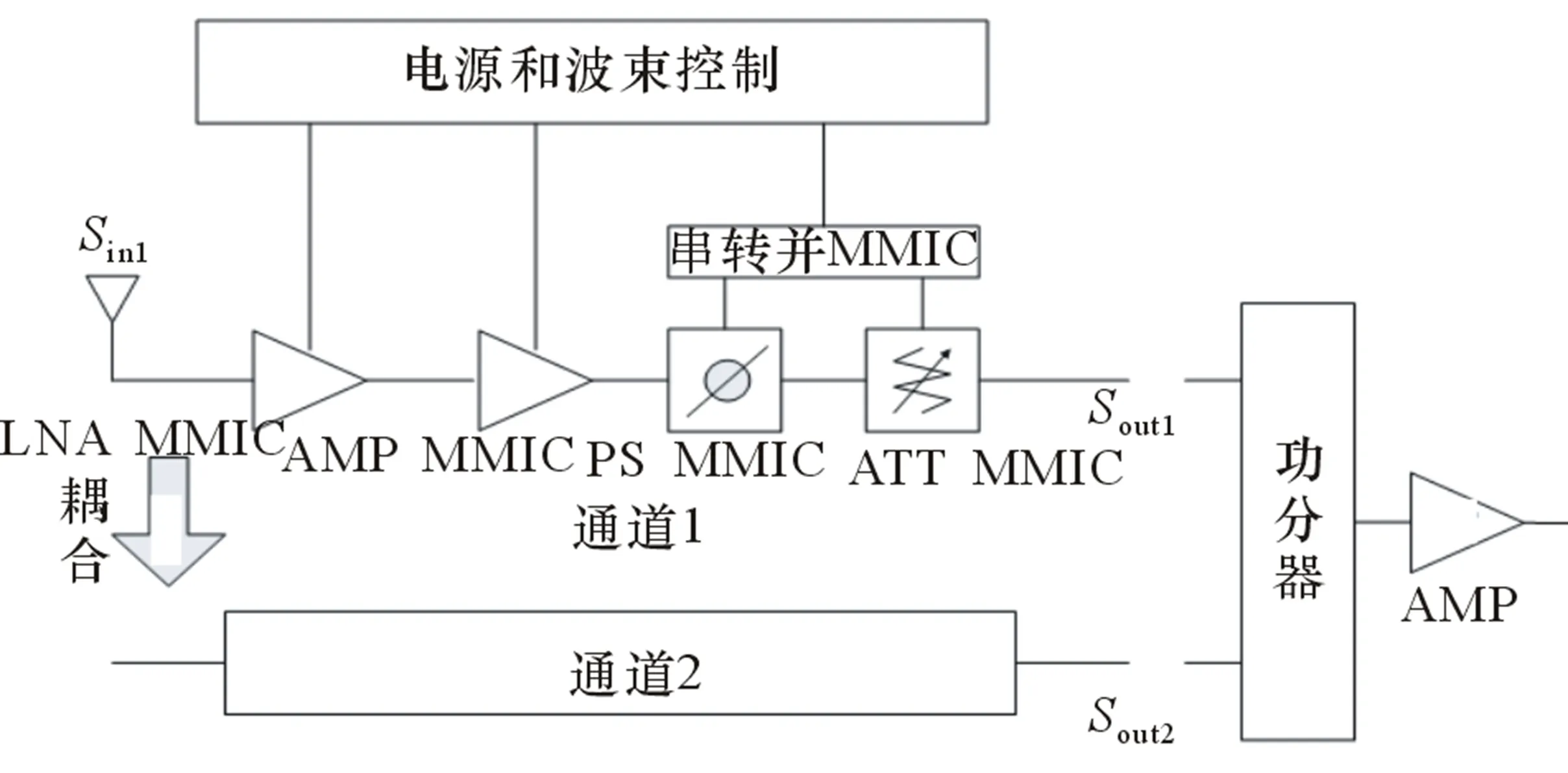
图1 两通道接收组件原理框图

通道2和通道1完全相同。为了降低链路噪声，第1个放大器选用低噪声放大器，然后经过第2个放大器后进入数控移相器和数控衰减器，2个通道信号再通过功分器进行合成，最后经过第3个放大器输出。

多通道接收组件的隔离度用来定义一个通道接收时，耦合到另一个通道的信号的相对大小用dB来表示。以图1为例，通道1和通道2同时加电工作，移相衰减器处于参考态，设2个通道的通道内增益(不含功分器部分)均为Gc(dB)，通道1输入端口信号大小为Sin1(dBm)，通道2输入端口接匹配负载，由于耦合，通道2输出端口测得信号功率为Sout2(dBm)，则两通道之间的隔离度DISO(dB，>0)为：

DISO=Sout1-Sout2=Sin1+Gc-Sout2

(1)

通道之间的这种耦合可能发生于通道内的任何地方，为了简化分析，结合实际情况，假设耦合在输入时产生，设耦合度为C(单位为dB，>0),则通道2的输入信号为Sin1-C(dBm),通道2的输出信号：

Sout2=Sin1-C+Gc

(2)

代入公式(1)，得到：

DISO=C

(3)

即隔离度等于耦合度。

移相指标通常包括移相精度和移相寄生调幅2个指标，其中移相精度定义为各个移相态的移相量相对于标称值的差值，移相寄生调幅定义为同一测试频点下，所有移相态增益的最大值与最小值之差。

2 分析和公式推导

见图1，理想情况下，2个通道之间完全隔离，通道1接收时没有信号耦合到通道2。而实际情况是2个通道的隔离度总是有限的，当通道1接收到信号后，由于两通道之间存在耦合，会有一部分能量进入到通道2，经过通道2的放大器放大后，和通道1的信号通过功分器合成输出，从而对通道1的移相指标产生影响。

为了得到描述耦合度和移相精度、移相寄生调幅关系的计算公式，设通道1的输入信号为Vmcos(ωt)，Vm为幅度值，ω为角频率。这里为了简化计算，初相φ定为0(rad)。设参考态时2个通道的通道内增益(不含功分器部分)均为G(无单位量)，为了简化计算，G只有实部，没有虚部，即通道内没有插入相移。

设通道1移相器的移相为φ，那么通道1进入功分器的信号为：

υ1=GVmcos(ωt+φ)

(4)

为了用相量法[6]进行计算，上面公式用相量表示为：

(5)

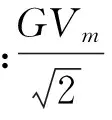
假设通道1和通道2的耦合度为C(dB，>0)，变换成无单位量的耦合度为：

(6)

通道2的移相器处于参考态，此时通道2进入功分器的信号为：

υ2=kGVmcos(ωt)

(7)

用相量表示为：

(8)

2路等分的Wilkinson功分器，设端口1为公共端口，其S参数[6]：

(9)

式中:-j表示Wilkinson功分器有-90°的相移，为了简化计算，合成时暂时不考虑-90°相移。

根据叠加定理[7]，功分器合成后的输出信号等于υ1和υ2单独输入时的输出信号之和，即输出信号为：

(10)

将上式用相量表示，并代入公式(5)、(8)得到：

(11)

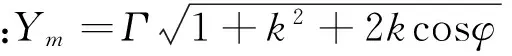
由于通道1的输入信号初相为0(rad)，那么通道1的移相器移相φ时，受通道2影响后的实际移相(rad)为:

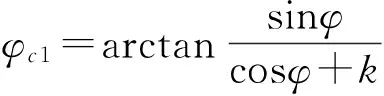
(12)

(13)

由公式(11),得到功分器合成后的输出功率Po(dBm)为:

(14)

那么，当通道1的移相器移相φ时，其增益GdB等于输出功率减去输入功率，即:

GdB=Po-Pi1

(15)

将公式(11)、(13)、(14) 代入上式，得到:

(16)

当通道1移相器处于参考态时，φ=0°，上式变为:

(17)

公式(16)减去公式(17)得到隔离度对移相寄生调幅影响的公式为:

(18)

公式(12)、(18)即为通道耦合度对移相精度和移相寄生调幅影响的计算公式。从公式中可以看出，不同频段的产品，只要通道隔离度相同，对移相指标的影响就相同。但实际情况下，由于毫米波频段辐射强，组件尺寸小，通道隔离度会比低频段的产品差得多。

利用上述公式，可以计算得到隔离度对移相指标影响的几种典型数据，如表1所示。

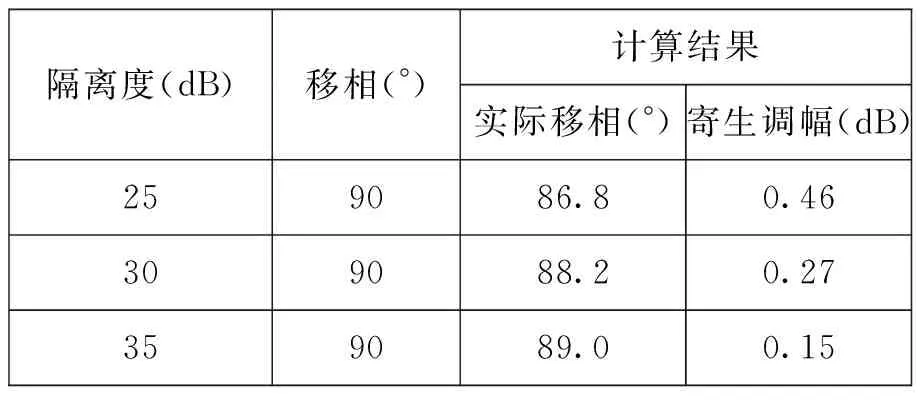
表1 通道隔离度对移相指标的影响

3 隔离度对移相影响的仿真

公式推导中进行了一些合理的简化，实际情况下通道初始相位可能不同，耦合时也会有相位差，为了研究复杂情况下隔离度对移相的影响，同时为了对上述公式进行验证，对设计原理图进行了仿真，如图2所示。

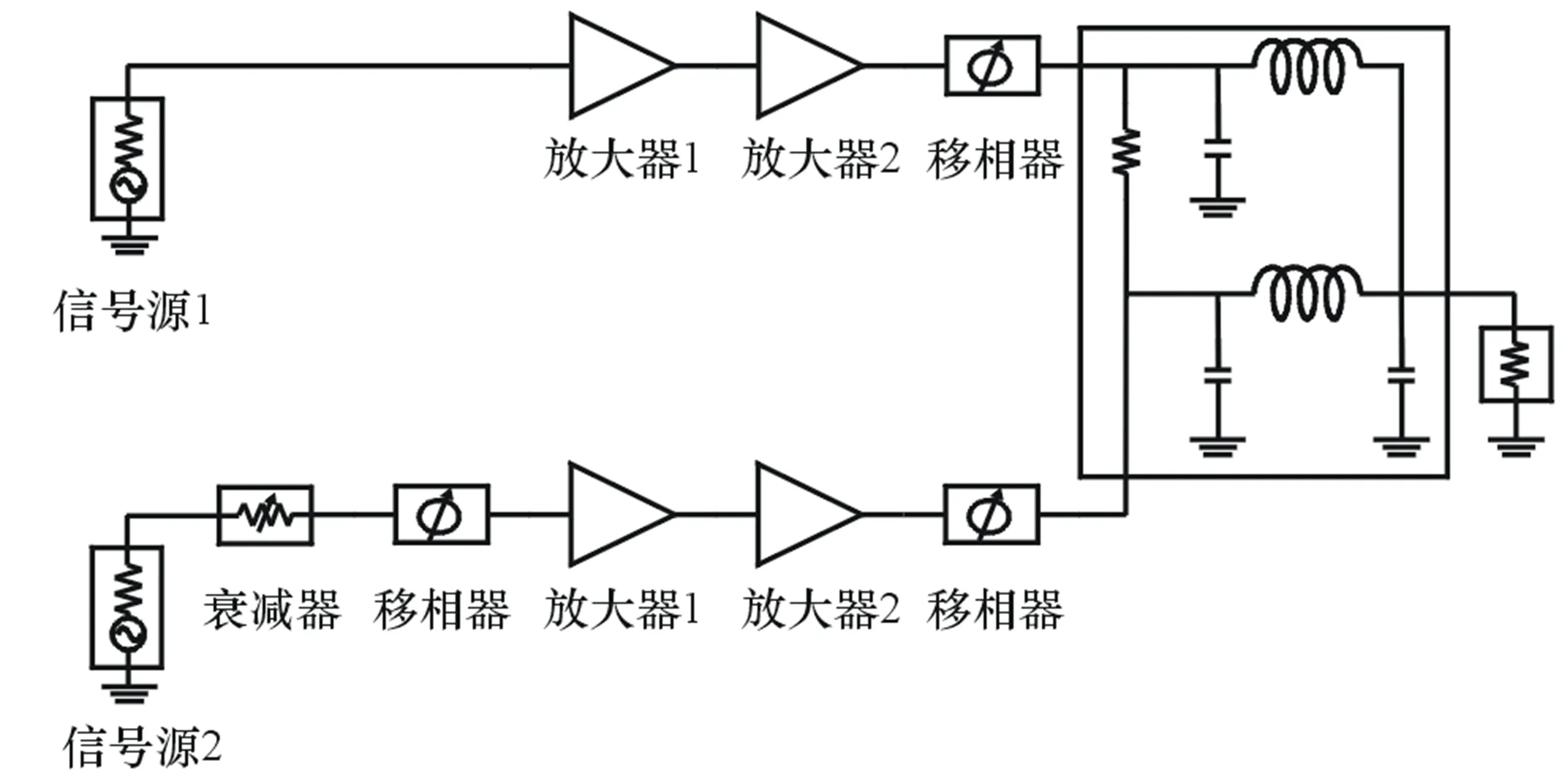
图2 隔离度对移相指标影响的仿真原理图

图2中，为了仿真2个通道信号的合成，使用了2个信号源，通道2的信号源后面连接衰减器来模拟耦合的幅度,移相器来模拟耦合的相位和通道初始相位的不一致，Wilkinson功分器使用等效的LC电路。对表1的情况进行了仿真，仿真结果与表1完全相同，计算公式和仿真互相得到了验证。

4 隔离度的改善

设计加工了一种四通道接收组件，包括通道内组件和功分器组件，如图3所示。微波芯片和串转并芯片均基于GaAsMMIC工艺。

图3 Ka波段4通道接收组件

设计加工了一种分腔式盖板，如图4，有效地减少了耦合，改善了通道隔离度。使用Mablab开发了移相指标的自动测试程序[8]，测试结果表明，改善隔离度后，该四通道接收组件在Ka波段获得了较好的移相指标，32态移相均方根≤4°，移相寄生调幅≤±0.6dB，满足工程使用要求。

图4 分腔式盖板

5 结束语

本文比较全面地研究了毫米波多通道接收组件通道隔离度对移相精度和移相寄生调幅的影响，对分析和解决毫米波多通道组件所有通道同时工作时移相变差的问题有较好的指导意义。用类似的分析方法，后续将研究通道隔离度对衰减精度和衰减寄生移相的影响。

[1] 黄建.毫米波有源相控阵TR组件集成技术[J].电讯技术，2011，51(2)：1-2.

[2] 张光义.相控阵雷达原理[M].北京:国防工业出版社，2009.

[3]CHIEHJS，PHAMAV.Alightweight8-elementbroadbandphasedarrayreceiveronliquidcrystalpolymer[C] //IEEEMTT-SInternational.California，USA，2010：985-986.

[4]JUNGYB.Multi-channelmoduledesignformobilesatellitecommunications[C] //IEEEAsia-pacificConferenceonCommunications.Busan，SouthKorea，2012：985-986.

[5] 刘晓莉，郝金中.Ka波段多通道发射组件的设计 [J].舰船电子对抗，2015，38(3)：99-102.

[6]POZARMD.MicrowaveEngineering[M].FourthEdition.USA:JohnWiley&Sons,Ltd,2012.

[7]NILSSONWJ，RIEDELAS.ElectricCircuits[M].9thed.USA：PrenticeHall，2011.

[8]Agilent.PNASeriesNetworkAnalyzerUser’sandProgrammingGuide[M].USA：AgilentTechnologies，2010.

Influence of Isolation of Millimeter-wave Multi-channel Receiving Module on Phase Shift

WU Hong-yu,LI Zhi-qiang,QIAO Ming-chang,ZHAO Zi-run

(The 13th Research Institute,CETC,Shijiazhuang 050051,China)

This paper introduces the typical principle block diagram of multi-channel receiving module,puts forward the concept of channel isolation and coupling degree,phase shift precision and phase shift parasitic amplitude modulation (AM),deduces the calculating formula of influence of channel coupling degree on phase shift precision and phase shift parasitic AM by means of vector method，indicates that the influence of isolation on phase shift indexes are irrelative with frequency theoretically.The influence of channel isolation on phase shift precision and phase shift parasitic AM are simulated by means of simulation software，the obtained values are same as the result obtained through formula calculation,they are validated by each other.The way to improve channel isolation is put forward,a Ka-band four-channel receiving module is designed and fabricated,the channel isolation is improved,better phase shift precision and phase shift parasitic AM are obtained in this paper.

millimeter-wave;multi-channel;isolation;phase shift precision;phase shift parasitic amplitude modulation

2016-01-23

TN957.5

A

CN32-1413(2016)03-0079-04

10.16426/j.cnki.jcdzdk.2016.03.020