Structural Damage Detection Using a Modified Artificial Bee Colony Algorithm

H.J.Xu,Z.H.Ding,Z.R.Lu,2,J.K.Liu

1 Introduction

Structure damage may be occurred by fatigue,corrosion and aging in normal service,or may be produced by impact loads,earthquake and wind.Negligence of local damage may cause serious engineering problems.Then the structural damage detection(SDD)is a hot topic in the field of structural health monitoring.Various approaches for damage detection have been studied and accepted by the engineering application.Specially,non-destructive approaches like techniques based on vibration response for damage identification have been widely studied in recent year.

Previous studies have shown that the associated physical changes in the structures may result in changes in dynamic characteristics of the system such as natural frequencies,mode shapes,damping ratios,modal strain energies et al.Therefore,de-tecting some of these properties of the system,the location and extent of the local damage could be identified.Then the vibration-based method as a no-destructive approach is utilized increasingly for its feasibility and efficiency.Hassiotis and Jeong(1993)utilized the natural frequencies to identify the local damage of structures.Then by applying the curvature mode shapes,Ratcliffe(1997)and Pandey,Biswas,and Samman(1991)localized the local damages effectively.Also,the modal strain energy and the flexibility were applied to damage detection by Yang,Liu,and Li(2013)and Shi,Law,and Zhang(2002).

With the development of the computer technique and mathematics,swarm intelligence technique gained its popularity.By transferring the local damage identification problem to the objective function optimizing problem,the local damage parameters can be gained by minimizing the objective function formulated of the difference between the measured value and the calculated value from the certain system.For instance,Shu,Zhang,Gonzalez,and Karoumi(2013)applied the Neural network(NN)for damage detection.Besides,Genetic Algorithm(GA)was chosen as an optimization tool using residual force method to solve damage detection problem by Mares and Surace(1996).Also some new optimization algorithms such as colony optimization algorithm,cuckoo search algorithm and particle swarm optimization algorithm have been introduced in damage detection by Xu,Liu,and Lu(2015)and Kang,Li,and Xu(2012a).However,these approaches mentioned above all have shortages in various aspects.Some of them are ineffective for symmetrical structures,some of them consume time,and others may have less feasibility.

It is noteworthy that,a new swarm intelligence called Artificial Bee Colony(ABC)was developed for numerical optimization problems by Karaboga(2005)in 2005,inspired by the bee colony’s behavior of seeking food source of high quality.It’s utilized increasingly for its feasibility and efficiency.

The ABC algorithm is simple in concept and is easy to implement.It has been applied in many areas like constrained optimization problems and multi-objective optimization problems.For example,it has been of hybrid use with Nelder-Mead simplex method to solve concrete dam structures by Kang,Li,and Xu(2009).Also,Sonmez(2011)utilized the ABC algorithm with a penalty function method for minimize the weight of truss structure.Then,ABC algorithm was introduced to the multi-objective design by Omkar,Senthilnath,Khandelwal,Naik,and Gopalakrishnan(2011).

The present damage detection application shows that ABC algorithm benefits the ease of implementation and has good robustness.But to the author’s knowledge,very few studies have been done on the application of the certain algorithm to complex structural damage detection.One of the complex structure systems is the coupled double-beam systems that can be treated as two parallel slender beams continuously connected by linear elastic layers[Huang and Liu(2013)].In this paper,we discuss the damage detection of a coupled double-beam system based on modified ABC algorithm.The numerical simulations show that both single damage and multiple damages in the systems can be identified successfully even under measurement noise,which shows that ABC algorithm is very promising for damage detection.

2 A brief introduction to ABC algorithm

The artificial bee colony algorithm is inspired by the bee colony’s behavior of seeking food source[Karaboga(2005)].In the process of feeding,the bee colony is divided in three groups.In the beginning,scout bees start processing forage and exploring food source randomly and share the information(including the quality and quantity about the food resource)on the dancing area.Some of them watch the dances of the employed bees and decide which the food source to exploit.This group named onlookers.

Then the onlookers select the best food resource,becoming employed bees simultaneously,and head to the best food resource.Meanwhile,they will exploit the better source in the neighborhood around the destination.If they discover a better place,they will abandon the primary selected place(“greedy selection rule”).

The last bee group is called scout bees.Regardless of food information,a scout will finds a new food source and starts to consume it,then it continues its work as an employed bees.Once the employed bees can’t find better source within the limited times,they will change back to the scout bee,and continue to explore food randomly.Overall,the scout bees are responsible for the exploration process while the onlookers and employed bees control the exploitation in the search space.

When refer to optimization problem,a food source position of the ABC algorithm is defined as a possible solution and the nectar quality of the food source matches the fitness of the related solution in optimization process.Because each employed bee is associated with only one food source,the number of employed bees is equal to the number of food sources.Then we set a population of n artificial bees placed randomly in the search space standing for the food source position,then the solutions is subjected to repeated iteration of the search process of the employed bees,scout bees and onlookers.

The process of the proposed ABC algorithm is given as follows:

Step 1.Set the sum of bees(n)and maximum number of iteration.

Step 2.Creat an initial bee colony randomly,assuming the solution is f dimension,then we have

AujandAljare the lower and upper bounds of thejth variable,respectively,and calculate every bee’s objective function valueg(Aj).

Step 3.Choose the best food location among the candidate food sources(n)based on their each function value.Then the bees which associated with the best locations become “employed bees”.

Step 4.Set iteration=1,loop over each food source(i=1,2,...,n/2).

4.1Calculate each employed bee’fitness value based onfit(.)function as below

4.2Once all the fitness functions have been determined,a fitness-proportional selection process is applied so that the probability of selection associated with thejth candidate can be show below

Eq.(3)represents roulette selection strategy,a food source with high value of the fitness function value that will have a higher chance to be selected.

Step 5.Give up the present food source if there is no improvement of the food after limit number of iterations.This process calls ‘scout bee phase’.These employed bees act as the colony’s explorers.They continues to find new food place randomly until they find rich and unknown food resource,and change to employed bees.This process may help algorithm overcome the trap of the local optimization.

Step 6.Iteration=iteration+1.

Step 7.If the iteration is greater than maximum cycle or there is no improvement in the best solution after certain iterations,terminate the iteration procedure,otherwise,go back to step 4.

3 Modification of the ABC algorithm

Damage detection problem may have several global optimal solution especially when the system is symmetric.In this paper,we modified the algorithm based on tournament selection strategy and chaotic search mechanism to avoid the local optimum.

3.1 Tournament selection strategy

The Tournament Selection Strategy reolaced the roulette wheel to enhance the global search ability.It first makes comparison of each solution’s fitness(including comparing with itself,that is,the worst solution can acquire at least one point),the bigger one will get one point.Then finish comparison,each solution γmwill acquire its total point αmand such total points will be used to calculate the selection probability based on Eq.(5).

where αmdenotes the total points of a solution γm.Compared with the roulette wheel,this strategy ensures that all solutions have a finite probability of selection,so those solutions with big fitness values do not overwhelm the search strategy.Thus the global search ability of algorithm is enhanced[Xu,Ding,Lu,and Liu(2015)].

3.2 Chaotic search mechanism

Chaos is a characteristic ofnon-linear systems,which is a bounded unstable dynamic behavior that exhibits sensitive dependence on initial conditions and includes infinite unstable periodic motions.Considering of its ergodicity,Chaotic Search Mechanism becomes a good pattern that can avoid the local optimum.

In this study,chaotic search mechanism is introduced to the scout bees phase.Because in scout phase,as mentioned above,if the solution couldn’t improve after limit times,the solution is abandoned.However,for the abandoned solution,the solution trapped in the local minima use to produce chaotic sequence and the best solution will be replaced the original solution(will be abandoned).Via such change,the solution ceased exploitation(will be abandoned)can continue to local search,which can increase the convergence rate and accuracy of the algorithm.

Assuming the ceased solution in ABC algorithm is Xk=(Xk1,Xk2,...,Xkd),Xki∈[ai,bi],we apply chaos optimum for the Xkiaccording to the procedures as follow

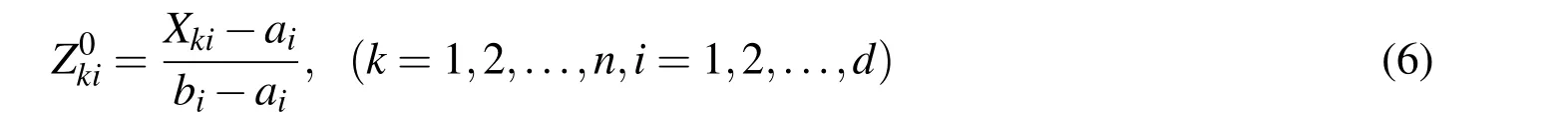
2.Using Eq.(5)producing chaotic series Zmk(m=1,2,...,Cmax),Cmaxis the maximum number of chaotic iteration.

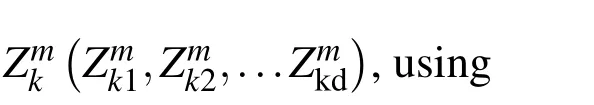
4.Sustaining the chaotic optimum iterations until reaching theCmax.

3.3 Procedures of modified ABC algorithm

1.Initialization based on step1,step2,step3 mentioned above.

2.Calculate Pibased on Eq.(5),and then pick up solutions.Then searching the adjacent source and apply Eq.(4)producing related new solutions and calculating their fitness value.After comparing the values,replace the solution by the better one.

3.Judging the existence of the stagnant solutions which means local optimum may occur.If stagnation exists,use chaotic search mechanism to produce the new solution.

4.Memorizing the best solution.

5.Estimate the solution meets the terminal conditions or not.If so,output the result,otherwise,go to step 2.

Above all,the iterative process of the proposed modified ABC algorithm is given on flow Chart 1.

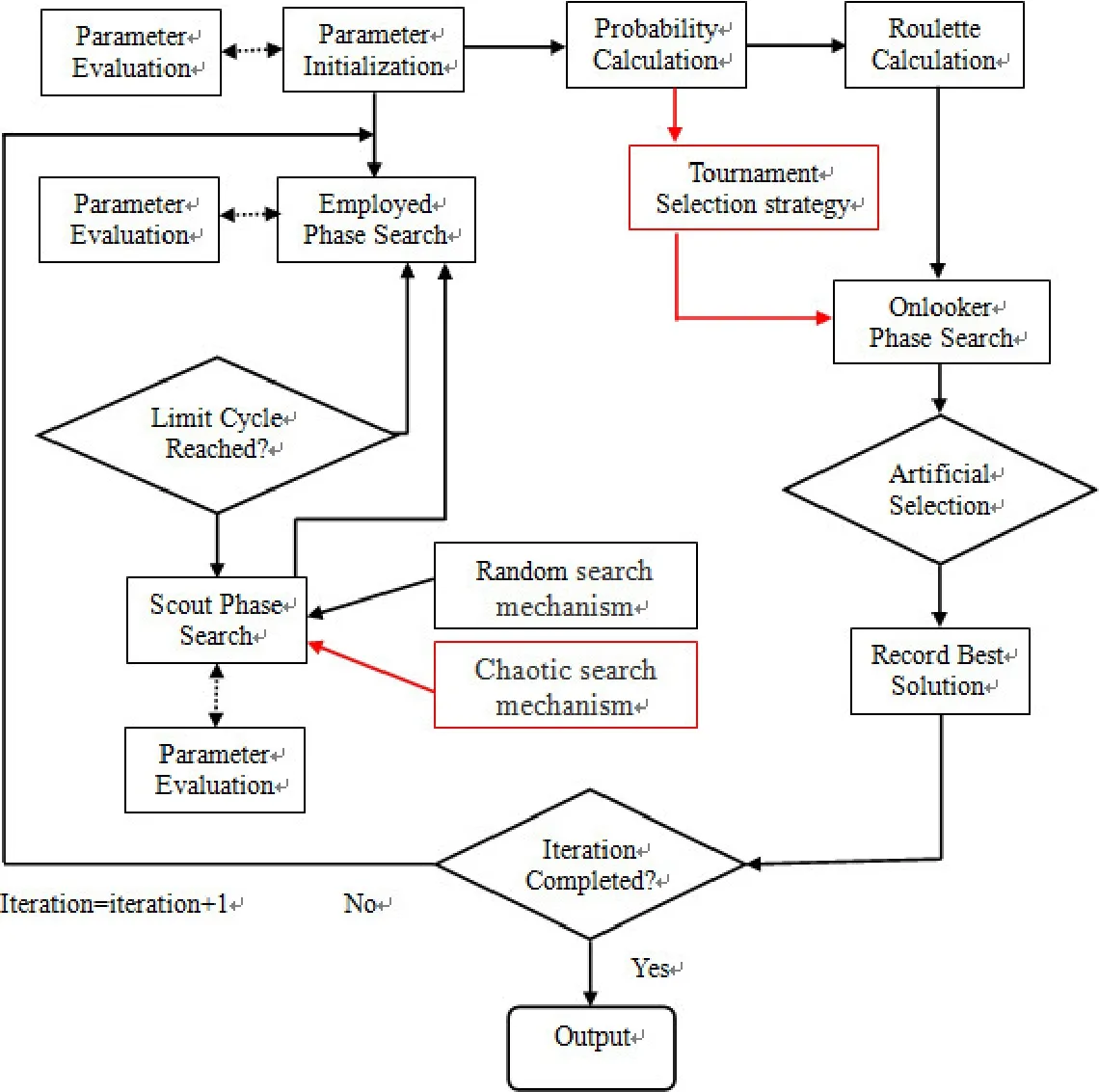
Chart 1:The iterative process of the proposed modified ABC algorithm(the red parts are improved)

4 Mathematical model

4.1 Parameterization of damage

In this paper,the certain algorithm is applied to a complex structure system called the coupled double-beam systems.The reasons are listed as follows.First of all,the coupled double-beam system has repeated or near frequencies phenomenon for the symmetry which can judge the effectiveness and accuracy of the method.Secondly,it is widely used in aerospace,automotive,sports equipment and other fields.Analysis of the damage detection of a couple double-beam systems based on a modified artificial bee colony algorithm can guide the engineering application.In general,a coupled double-beam system(showed in Figure.1)which consists of two beams coupled via a set of linear springs is selected as an example[Huang and Liu(2013)].The system is assumed to be simply supported except otherwise specified.

Figure 1:The coupled double-beam system(1,11,12,22:node number of FEM).

Applying free interface substructure method,the lower and upper beams are treated as two independent beams without considering the coupling springs[Lu,Liu,Huang,and Xu(2009)].The equation of motions of the each beam can be expressed as

where Mu,Ml,Cu,Cl,Ku,Klare the system mass matrix,damping matrix and stiffness matrix of the lower beam and upper beam,respectively.Rayleigh damping model is adopted to build up the damping matrix.T{F(t)}is the equivalent nodal force vector.

Then consider the coupling inner springs,the equation of motions of the system can be written as

Rewriting Eq.(10)and Eq.(11)in matrix form

Eq.(12)can bexpressed in a more simple form

The eigenvalue equation for a finite element model of the system as discussed above is

where M and K are the structural mass matrix and stiffness matrix,respectively.And ωjis the jth natural frequency and φjis the corresponding mode shape.

Local damage in ts system is introduced as a perturbation in the elemental flexural rigidity and the other properties remain unchanged.This is similar to some researchers by introducing the concept of the damage parameter in the element of the system,but the other properties remain unchanged[Patil and Maiti(2003)].

When a structure with nel elements is damaged,the reduction of the stiffness can be evaluated by a set of damage parameters ai(i=1,2,...nel).The value range of parameter aiis between 0 and 1.When ai=1,means that the ith element is intact while ai=0,it represents that system is completely damaged.And then the stiffness matrix of the damaged coupled double system can be written as

where Kdis the stiffness matrix of the damaged system,and keipresents the ith elemental stiffness matrix in the global form.Based on this damage model,damage identification implies to identify each value in the damage parameter vector{a},based on the damage model mentioned above.

4.2 Objective function based on the vibration data

As mentioned abe,structural damage will lead to the changes of dymanic characteristic.On thether hand,we can use these modal data to formulate the objective function for damage identification.Considering the frequencies and mode shape data,modal assurance criteria(MAC)is utilized[Brehm,Zabel,and Bucher(2010)].The MAC is expressed as

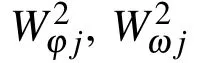
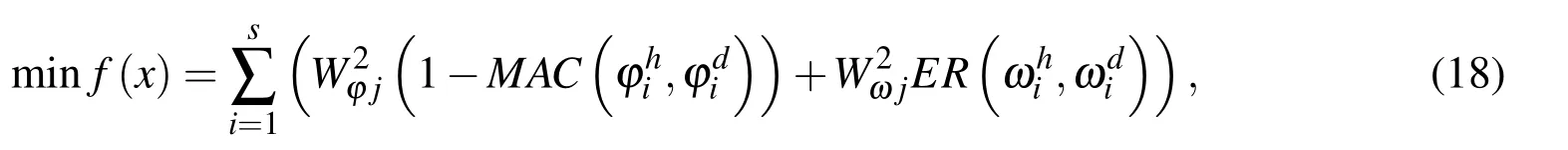
In the inverse problem,the damage vector is identified to indicate the damage extent of structure.In this study,for simplicity,all the factor values are taken as 1.If the value of damage parameter vector aimatches the given particular damage condition,the objective function will achieve its minimum value 0.In other words,when the minimum value of the objective function is identified,the corresponding parameter vector{ai}will indicate damage status of the structure.Then based on the value of the identify parameters ai,we can find out the local damages of the system.

5 Numerical simulations

As mentioned above,the coupled double beams system is adopted to verify the effectiveness of the proposed algorithms.In this section,we select the steel beam as the material of the coupled system.Then the physical parameters of the upper and lower steel beams are as below:Young’smodulus E1=E2=210GPa,mass density ρ1= ρ2=7800 kg/m3,the width b1=b2=0.15 m,the depth h1=h2=0.15 m,sectional inertia moment I1=I2=(1/12)bh3,the length L1=L2=10 m.The coefficient of the weakly coupling springs is taken as Kr=1×105N/m,and the coefficient of the strongly coupling springs is taken as Kr=1×109N/m.Coupled double-beam system is discretized into 20 Euler-Bernoulli beam elements with 22 nodes.The damage scenarios of the coupled double-beam system are showed in Table.1.

Table 1:Damage Scenarios of the coupled double-beam system

Situation 1:The strongly coupled double-beam system

In this situation,the first twelve natural frequencies of the certain system are showed in Table.2.

Table 2:The natural frequencies of the coupled double-beam system

From the Table.2,we can find that the repeated and near frequencies phenomenon is occurred under weakly coupled condition.This phenomenon may confuse some damage detection methods depending on the frequencies of the system,but the proposed method referred in this paper is not one of them.

Then we set the initial colony number is 50,limit number of cycle is 1000,iteration number is 500 and number of the runs is 1 separately.By using MATLAB software,we can calculate the objective function by ABC algorithm and Modified-ABC algorithm.To include the uncertainty in the measured data and to study the noise sensitivity of ABC,uniformly distributed random noise is added to measured data in the numerical simulation.To simulate measurement noise,the natural frequencies are contaminated with 1%noise and 3%noise is added to the modal displacement for all the cases[Kang,Li,and Xu(2012b)].To show the utility of the present approach,the first four natural frequencies and mode shapes of the coupled system are calculated.The iteration process of the strongly coupled double-beam system by ABC and M-ABC is showed in Figure.2.

Figure 2:The iteration process of the strongly coupled double-beam system by ABC algorithm and M-ABC algorithm

Besides,all the data have been calculated 10 times for stability and accuracy as showed in Figure 3 and Figure 4.Above all,we can see the average results of the damge detection by ABC algorithm and M-ABC algorithm,as showed in Figure 5.

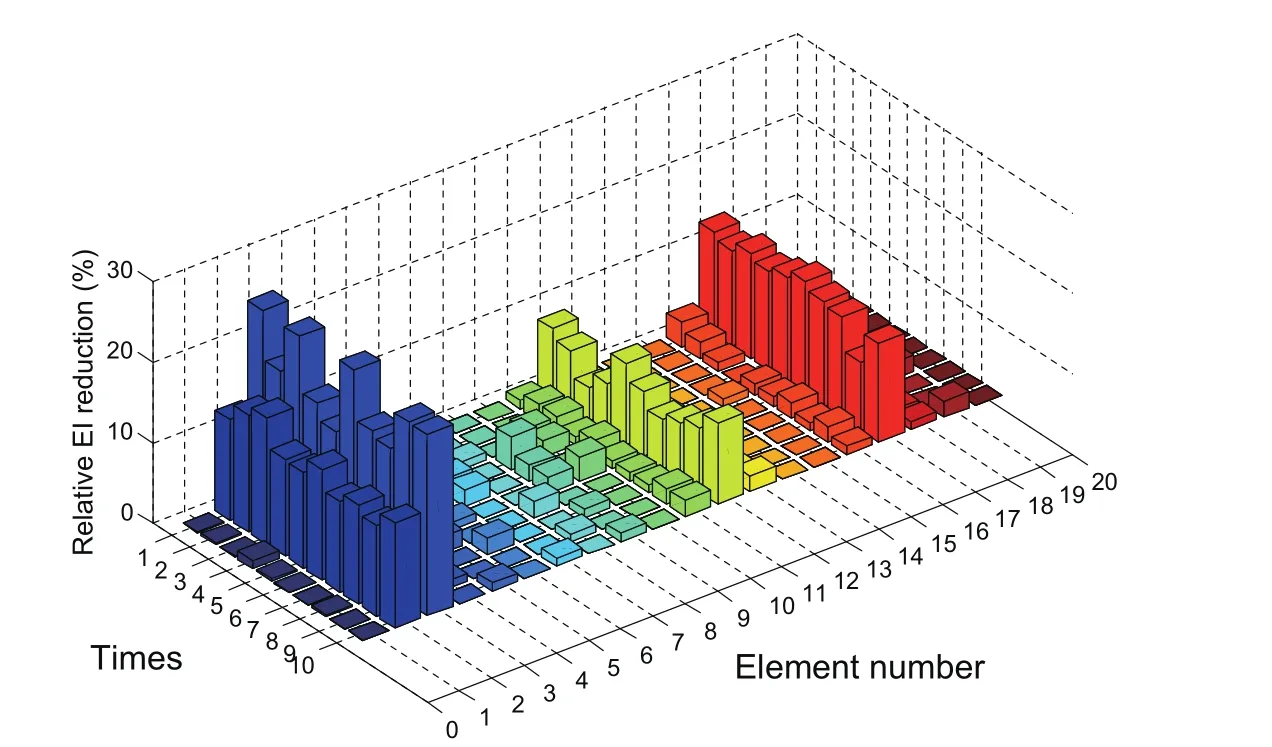
Figure 3:The damage detection data of the strongly coupled system by ABC algorithm

From the the Figure 5,we can find the damage location and damage degrees of the certain sytem.For more intuitive,we select the certain damage elements to further anlysis.The iteration of the certain damage elements by ABC algorithm and M-ABC algorithm is showed in Figure 6 and Figure 7 seperatively.

By comparing the detection result of the strongly double-beam system with artificial measurement noise to assumed damage showed in Figure 3,the largest error of ABC algorithm is 5.192%in 2th element,and the largest error of M-ABC is 2.22%in 3th element.Then we can find out the modified ABC algorithm is more effective than ABC algorithm,besides,M-ABC is insensitive for the measurement noise and can introduce to engineering application.

Figure 4:The damage detection data of the strongly coupled system by M-ABC algorithm

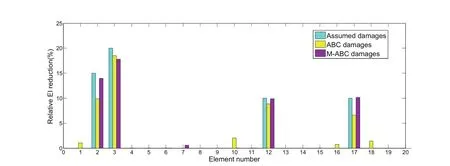
Figure 5:Comparison of the average results for the strongly coupled double-beam system under artificial measurement noise

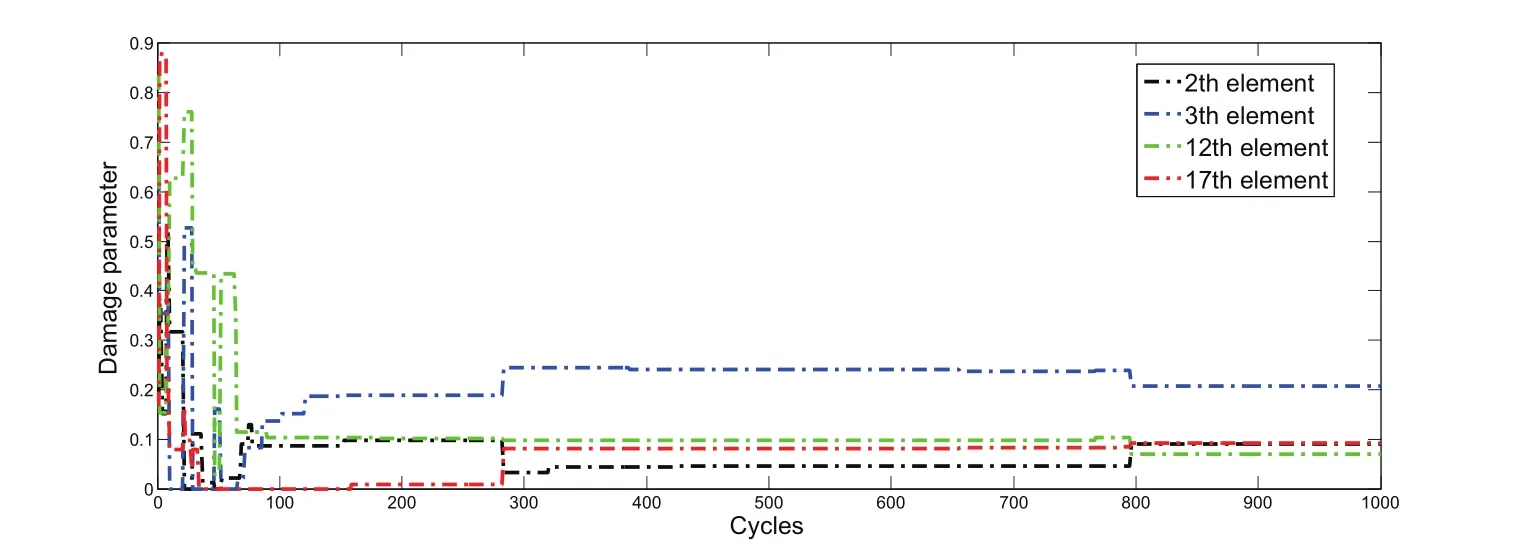
Figure 6:A close view of the damage elements by ABC algorithm

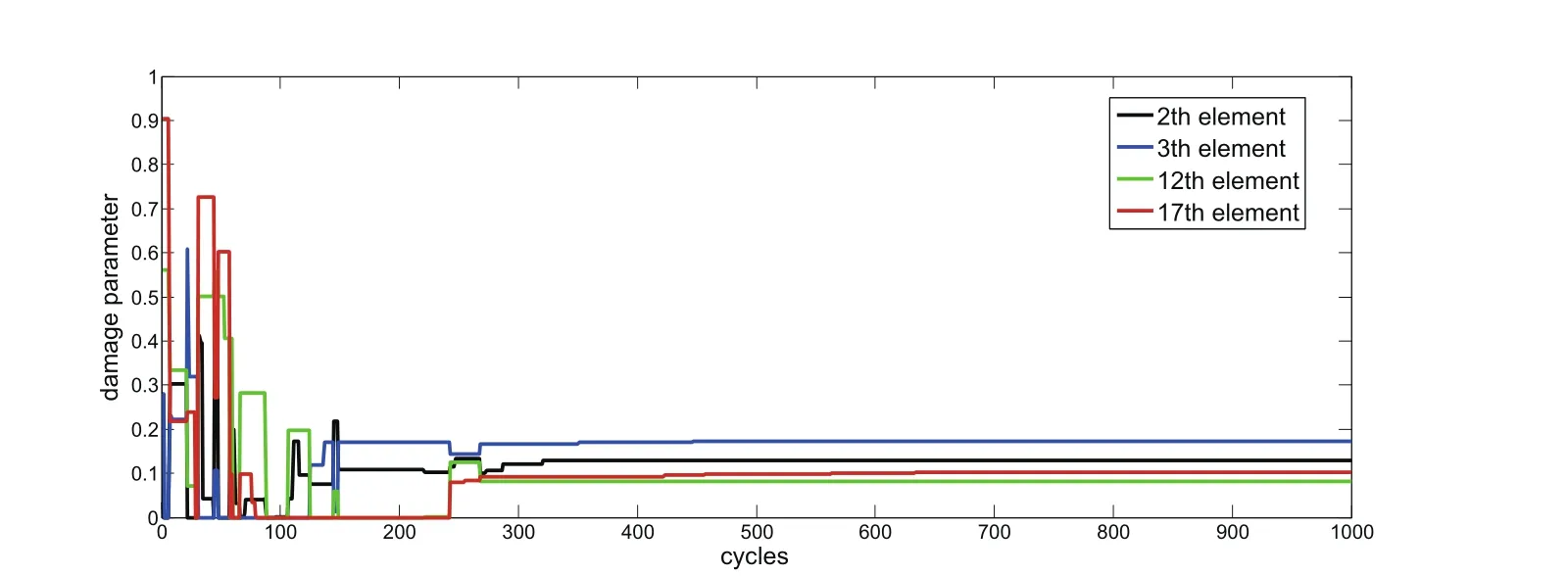
Figure 7:A close view of the damage elements by M-ABC algorithm

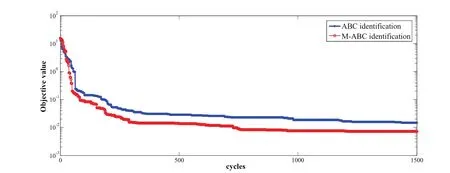
Figure 8:The Iteration process of the weakly coupled double-beam system by ABC algorithm and M-ABC algorithm.

Situation 2:The weakly coupled double-beam system

In this situation,the damage detection of the weakly coupled double-beam system with measurement noise is studied.The coefficients of the weakly coupling springs is taken asKr=1×105N/m.The initial value for the modified ABC algorithm and the measurement noise is uniform as mentioned above.The iteration process of the certain system with the same measurement noise as situation 1 is showed in Figure 8.all the datas have been calculated 10 times for stability and accuracy as shown in Figure 9 and Figure 10.Besides,we can see the average results of the damge detection by ABC algorithm and M-ABC algorithm,as showed in Figure11.From the the Figure11,we can find the damage location and damage degrees of the damaged system.What’s more,we select the certain damage elements to analyse their iteration processes as showed in Figure 12 and Figure 13 seperatively.

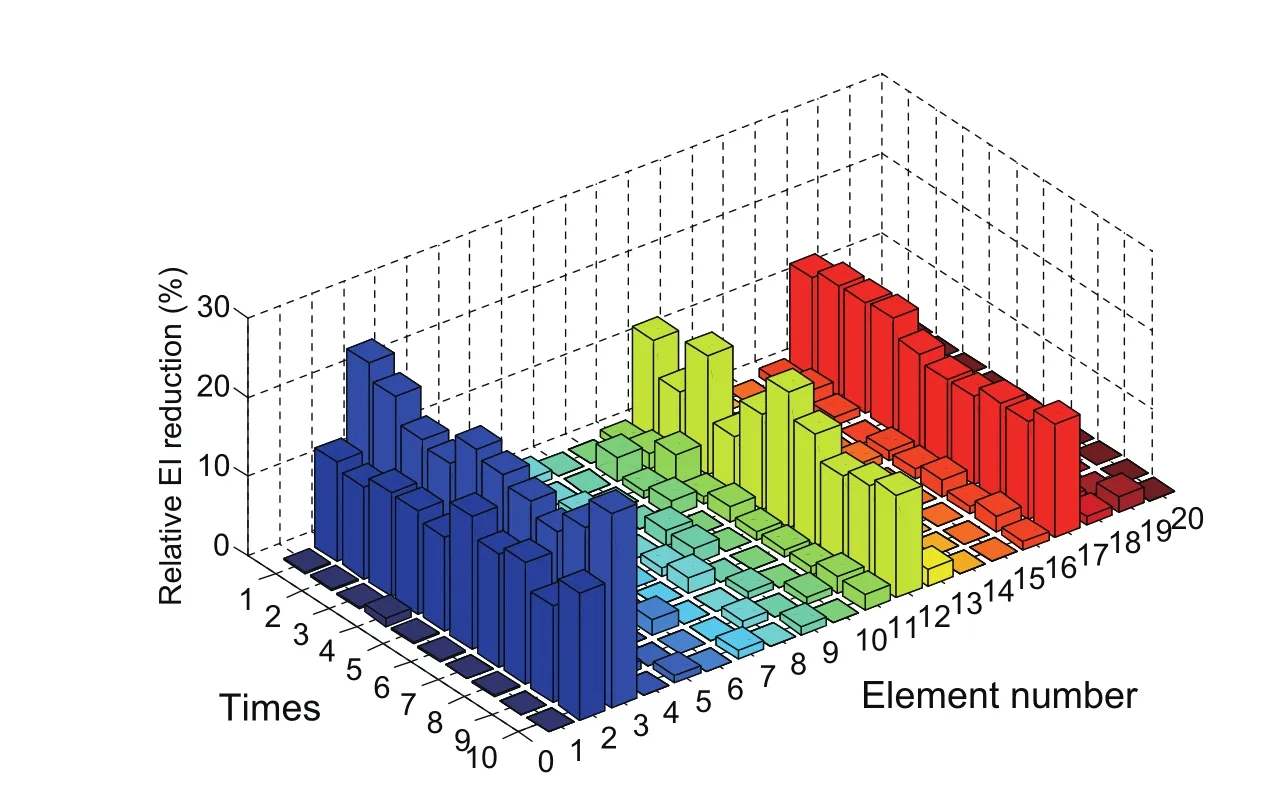
Figure 9:The damage detection data of the weakly coupled system by ABC algorithm

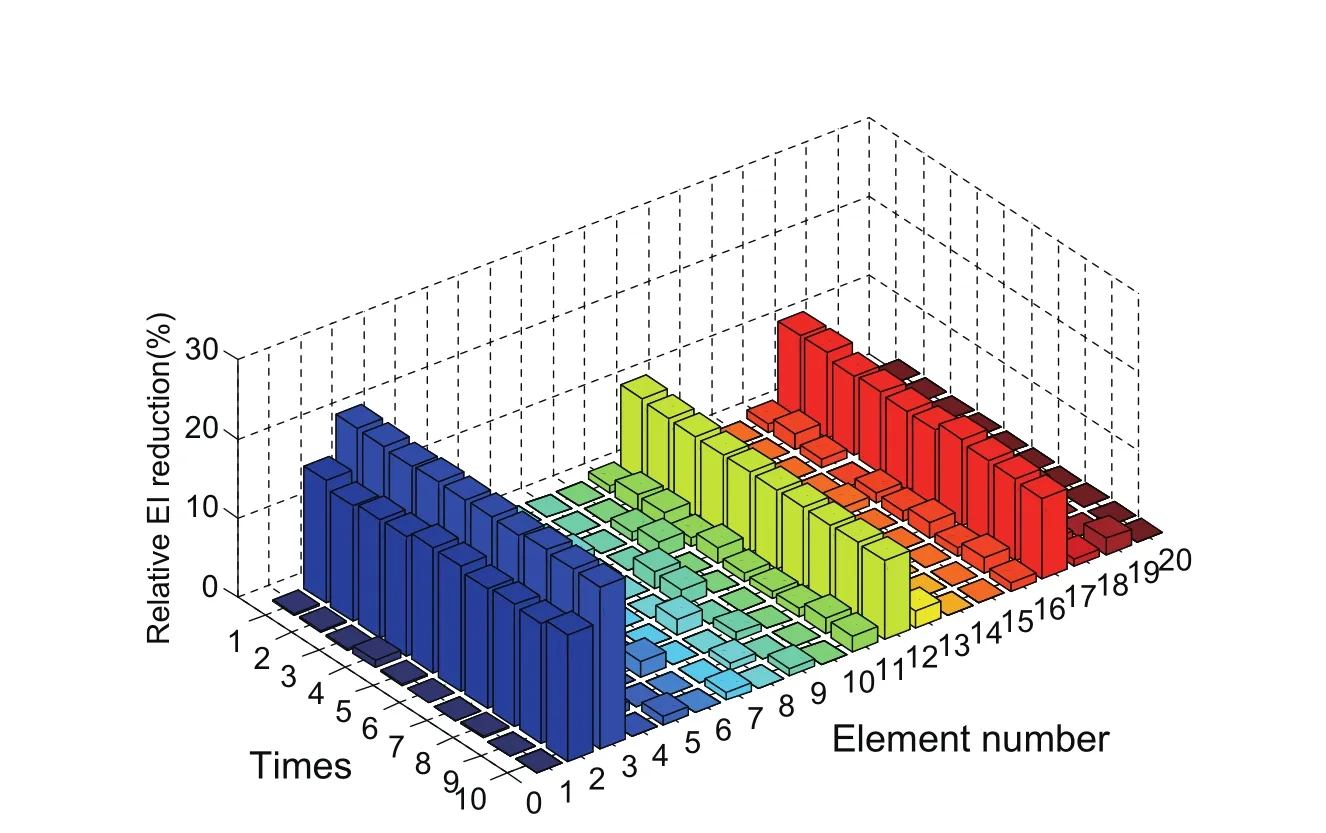
Figure 10:The damage detection data of the weakly coupled system by M-ABC algorithm

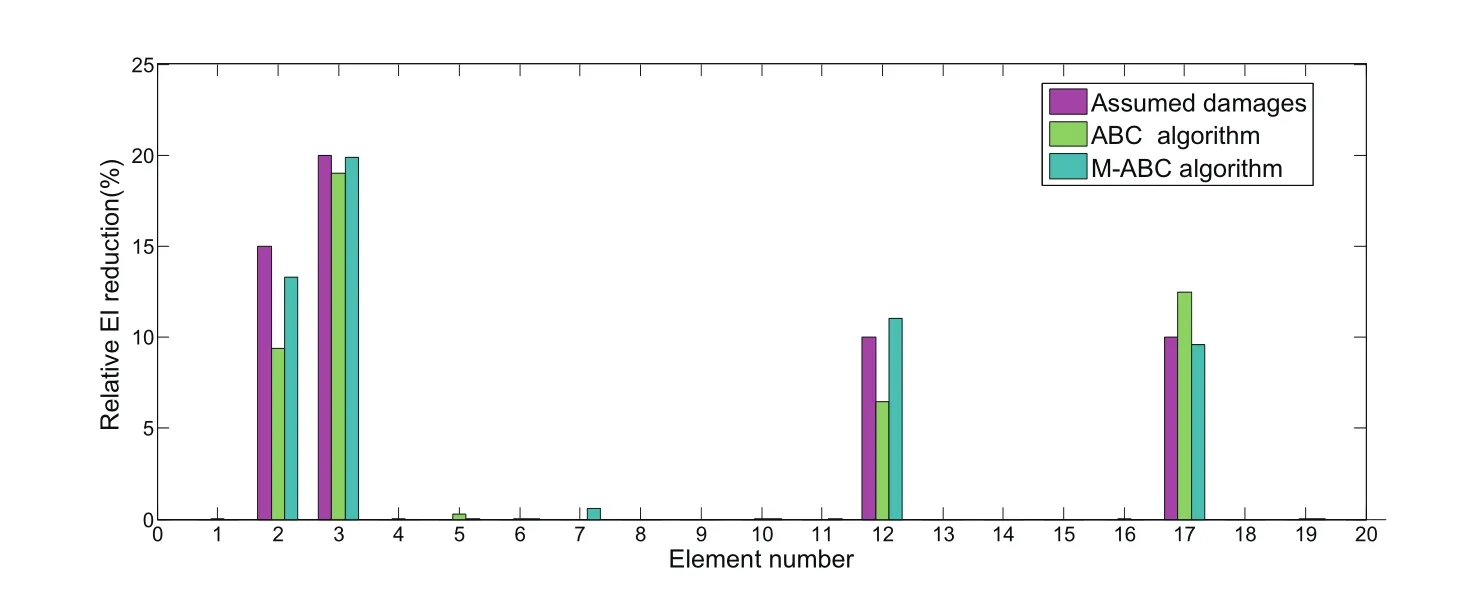
Figure 11:Comparison of the average results for the weakly coupled double-beam system under artificial measurement noise

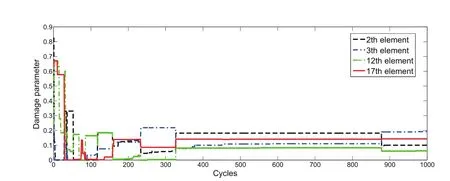
Figure 12:A close view of the damage elements by ABC algorithm

By comparing the detection result showed in Figure 11,the largest error of ABC algorithm is 5.59%in 2th element,and the largest error of M-ABC is 1.72%in 2th element.Then we can find out the modified ABC algorithm is more effective than ABC algorithm,besides,M-ABC is insensitive for the measurement noise and can introduce to engineering application.

Situation 3:a simple supported beam

In order to further verify the effectiveness of the M-ABC algorithm,a simple supported beam is studied.

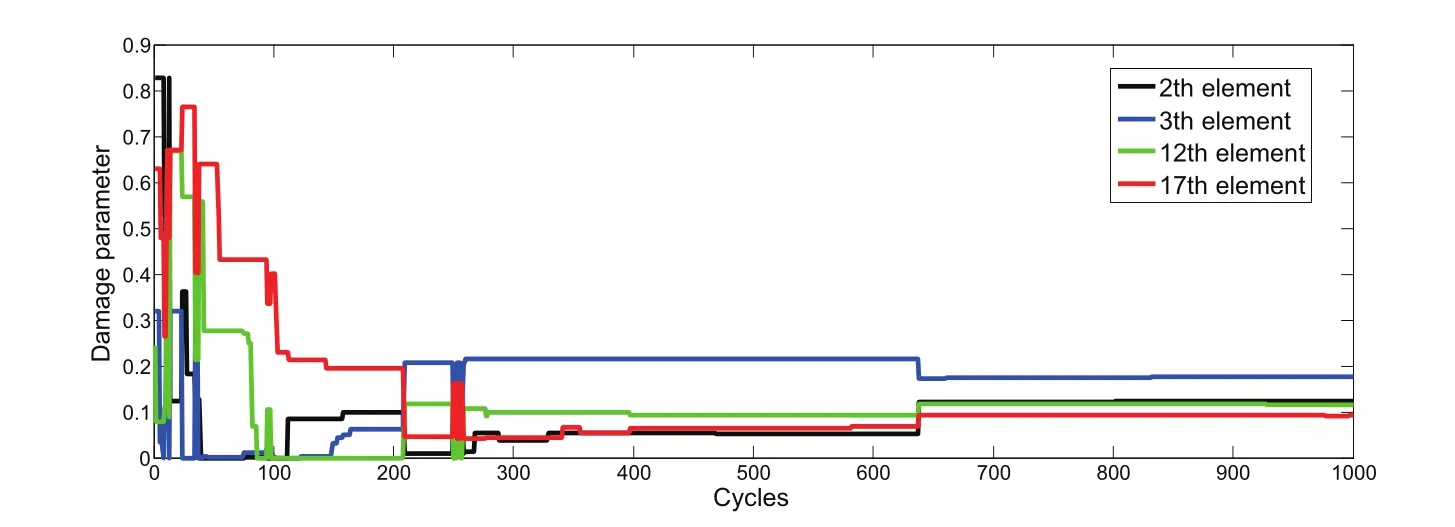
Figure 13:A close view of the damage elements by M-ABC algorithm

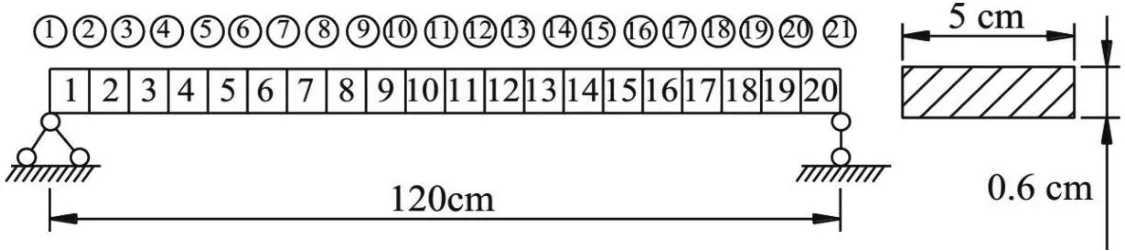
Figure 14:A simple supported beam

Figure 14 illustrates the geometric characteristics of the beam.The total number of elements and nodes are 20 and 21,respectively.Young’s modulus of the system is 210 GPa,mass density is 7.8×103kg/m3,the beam length is 120 cm.The first 3 natural frequencies and modes shapes are utilized.

In this case it is assumed that element 7 have 10%reduction in stiffness meanwhile element 8 has 15%,element 16 has 20%,respectively.And element 7 and element 8 are two adjacent elements.The curves of fitness values for M-ABC are demonstrated in Figure 15.Damage detection results are shown in Figure 17.The evolutionary processes of damaged element in are shown in Figure 18,proving all the damaged elements can be found correctly.What needed to be emphasized is that all these data were collected 10 times for average as showed in Figure 16.

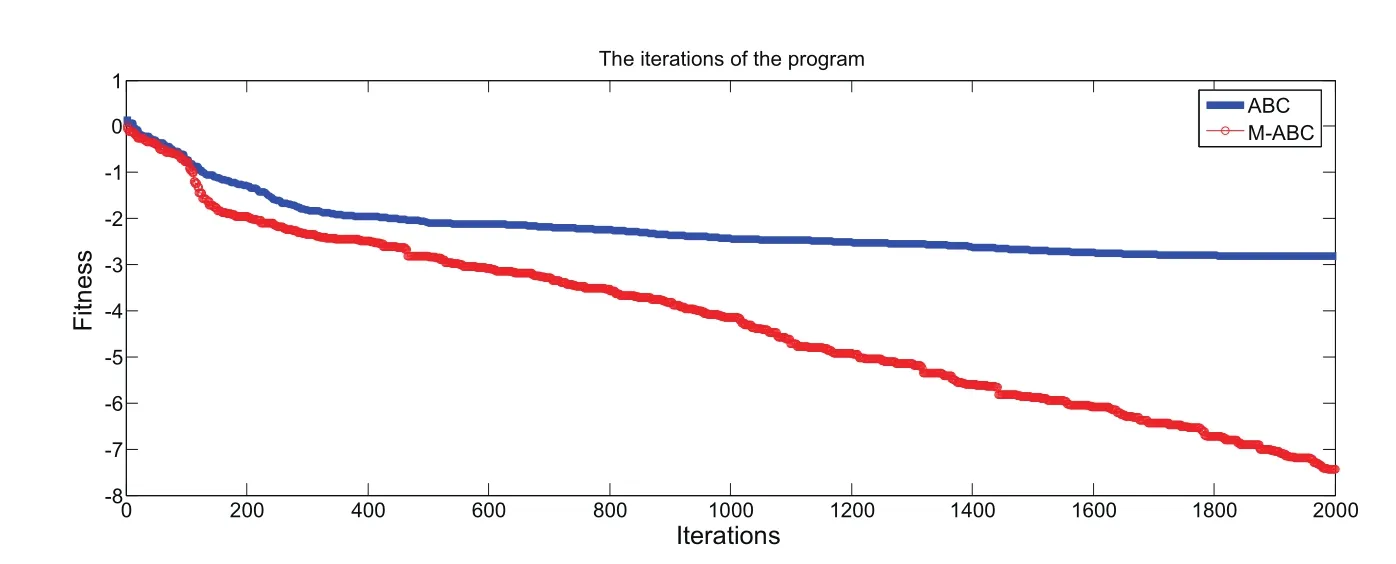
Figure 15:The Iteration process of the simple supported beam by ABC algorithm and M-ABC algorithm.

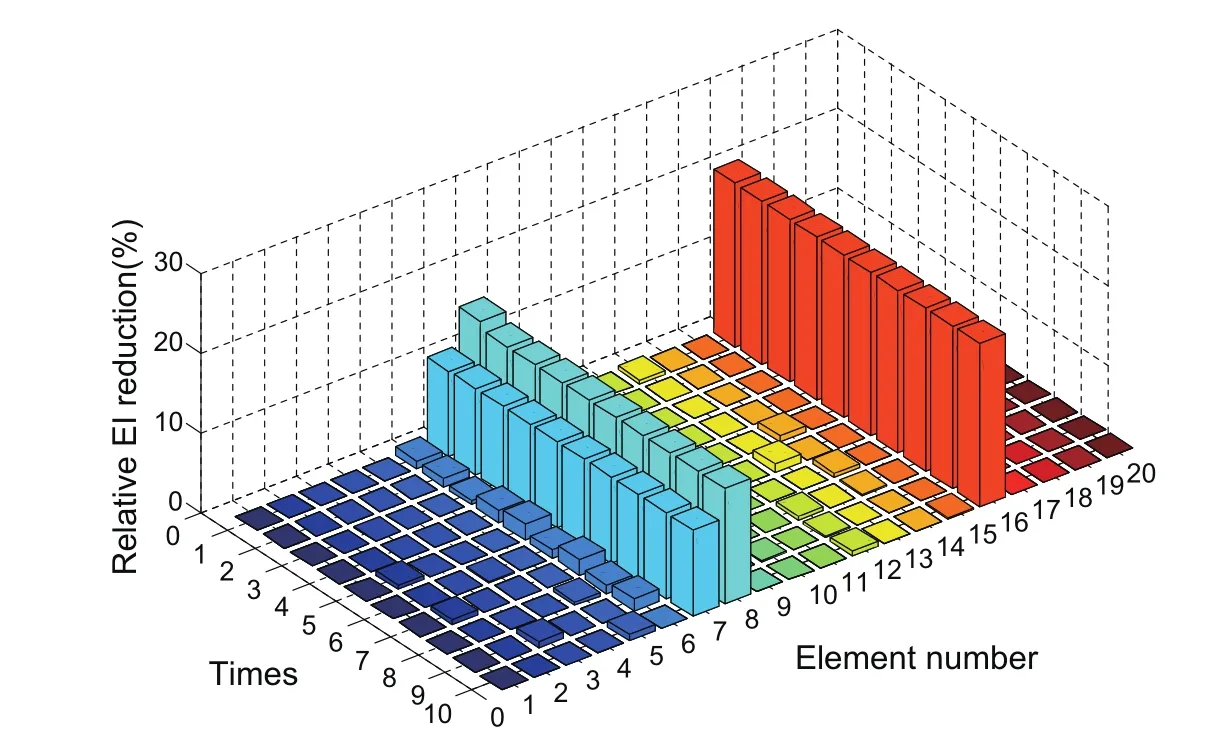
Figure 16:The damage detection data of the simple supported beam by M-ABC algorithm

Figure 17:Comparison of the average results for the simple supported beam under artificial measurement noise

By comparing the detection result of the simple supported beam with artificial measurement noise to assumed damage showed in Figure 17,the largest error of ABC algorithm is 2.5%in 8th element,and the largest error of M-ABC is 1.72%in 1th element.Then we can find out the modified ABC algorithm is more effective than ABC algorithm.

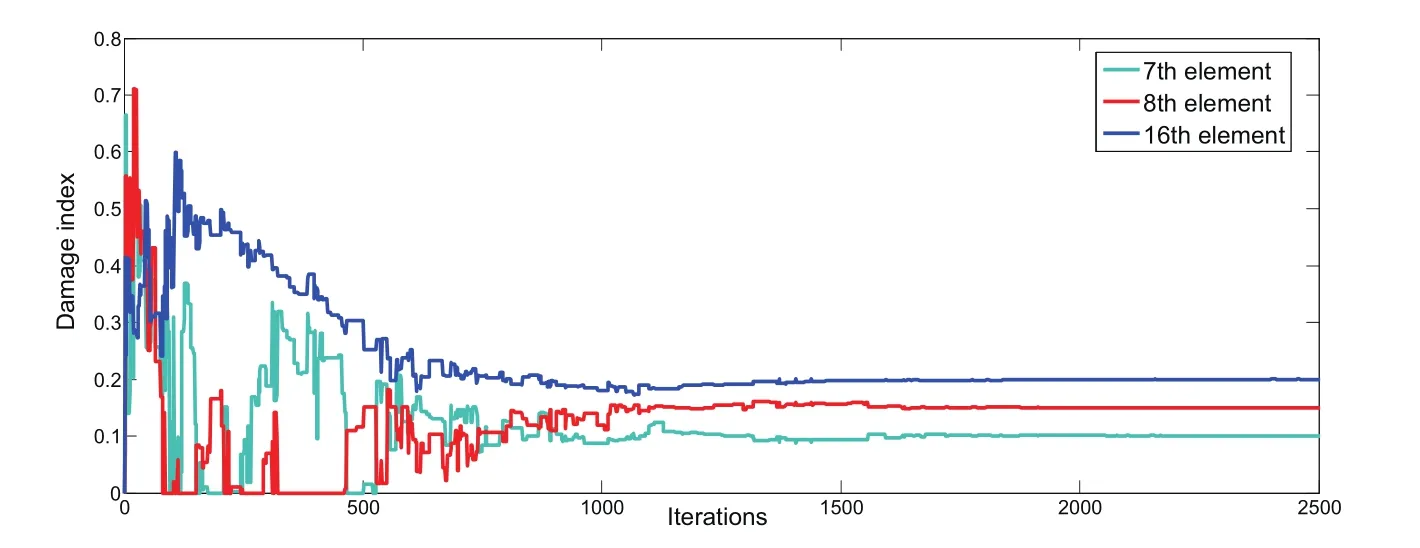
Figure 18:A close view of the damage elements by M-ABC algorithm

6 Conclusions

A structural damage identification(SDD)method based on the ABC algorithm and modified ABC algorithm using vibration data is investigated in this work.In the modified algorithm,the tournament selection mechanism(TSM)is chosen instead of roulette mechanism,chaotic search mechanism(CSM)is also introduced to improve the algorithm’s convergence rate and accuracy.By applying modal assurance criteria(MAC),the damage detection of a coupled double-beam system based on modified artificial bee colony(M-ABC)algorithm is studied.Numerical simulations demonstrate that the modified ABC algorithm is more effective for local damages identification in strongly(weakly)coupled double-beam system compared the ABC algorithm,and is insensitive to artificial measurement noise.Above all,the proposed method is of great potentiality for engineering application.

Acknowledgement:This work is supported by the National Natural Science Foundation of China(11172333,11272361),the Fundamental Research Funds for the Central Universities(13lgzd06),Doctoral Program Foundation of Ministry of E-ducation of China(20130171110039),and the Guangdong Province Science and Technology Program(2012A030200011).Such financial aids are gratefully acknowledged.

Brehm,M.;Zabel,V.;Bucher,C.(2010): An automatic mode pairing strategy using an enhanced modal assurance criterion based on modal strain energies.Journal of Sound and Vibration,vol.329,no.25,pp.5375-5392.

Hassiotis,S.;Jeong,G.(1993): Assessment of structural damage from natural frequency measurements.Computers&Structures,vol.49,no.4,pp.679-691.

Huang,M.;Liu,J.(2013): Substructural method for vibration analysis of the elastically connected double-beam system.Advances in Structural Engineering,vol.16,no.2,pp.365-377.

Kang,F.;Li,J.;Xu,Q.(2009): Structural inverse analysis by hybrid simplex artificial bee colony algorithms.Computers&Structures,vol.87,no.13,pp.861-870.

Kang,F.;Li,J.-J.;Xu,Q.(2012):Damage detection based on improved particle swarm optimization using vibration data.Applied Soft Computing,vol.12,no.8,pp.2329-2335.

Kang,F.;Li,J.-J.;Xu,Q.(2012):Damage detection based on improved particle swarm optimization using vibration data.Applied Soft Computing,vol.12,no.8,pp.2329-2335.

Karaboga,D.(2005): An idea based on honey bee swarm for numerical optimization.Technical report,Technical report-tr06,Erciyes university,engineering faculty,computer engineering department,2005.

Lu,Z.;Liu,J.;Huang,M.;Xu,W.(2009): Identification of local damages in coupled beam systems from measured dynamic responses.Journal of Sound and Vibration,vol.326,no.1,pp.177-189.

Mares,C.;Surace,C.(1996): An application of genetic algorithms to identify damage in elastic structures.Journal of sound and vibration,vol.195,no.2,pp.195-215.

Omkar,S.;Senthilnath,J.;Khandelwal,R.;Naik,G.N.;Gopalakrishnan,S.(2011): Artificial bee colony(abc)for multi-objective design optimization of composite structures.Applied Soft Computing,vol.11,no.1,pp.489-499.

Pandey,A.;Biswas,M.;Samman,M.(1991):Damage detection from changes in curvature mode shapes.Journal of sound and vibration,vol.145,no.2,pp.321-332.

Patil,D.;Maiti,S.(2003): Detection of multiple cracks using frequency measurements.Engineering Fracture Mechanics,vol.70,no.12,pp.1553-1572.

Ratcliffe,C.P.(1997):Damage detection using a modified laplacian operator on mode shape data.Journal of Sound and Vibration,vol.204,no.3,pp.505-517.

Shi,Z.;Law,S.;Zhang,L.(2002): Improved damage quantification from elemental modal strain energy change.Journal of engineering mechanics,vol.128,no.5,pp.521-529.

Shu,J.;Zhang,Z.;Gonzalez,I.;Karoumi,R.(2013): The application of a damage detection method using artificial neural network and train-induced vibrations on a simplified railway bridge model.Engineering structures,vol.52,pp.408-421.

Sonmez,M.(2011): Artificial bee colony algorithm for optimization of truss structures.Applied Soft Computing,vol.11,no.2,pp.2406-2418.

Xu,H.;Ding,Z.;Lu,Z.;Liu,J.(2015): Structural damage detection based on chaotic artificial bee colony algorithm.Structural Engineering and Mechanics,vol.55,no.6,pp.1223-1239.

Xu,H.;Liu,J.;Lu,Z.(2015): 1.structural damage identification based on cuckoo search algorithm.Journal of Mathematical Models in Engineering(MME),vol.1,no.1,pp.1-12.

Yang,Q.;Liu,J.;Li,C.(2013): Multiple-damage detection using the best achievable flexibility change.Computer Modeling in Engineering&Sciences,vol.91,no.4,pp.313-335.