A Piecewise Linear Isotropic-Kinematic Hardening Model with Semi-Implicit Rules for Cyclic Loading and Its Parameter Identification

M.Ohsaki,T.Miyamuraand J.Y.Zhang

1 Introduction

In the design process of building frames,accurate estimation of elastoplastic responses is very important,because such structures are supposed to dissipate seismic energy through plastic deformation.Elastoplastic responses of building frames are usually simulated using macro models such as plastic hinges and fiber elements.However,owing to recent progress of computer technology and due to increasingdemands for accurate estimation of seismic responses,finite element analysis using solid elements has been extensively investigated[Ohsaki,Miyamura,Kohiyama,Hori,Noguchi,Akiba,Kajiwara,Ine(2009)].

A software package called E-Simulator is under development at the National Research Institute of Earth Science and Disaster Prevention(NIED),Japan.E-simulator is a parallel finite element analysis software package for precisely simulating collapse behaviors of building and civil structures[Miyamura,Yamashita,Akiba,Ohsaki(2015);Miyamura,Ohsaki,Kohiyama,Isobe,Onda,Akiba,Hori,Kajiwara,Ine(2011)],and it is based on a commercial software package called ADVENTURECluster[Allied Engineering(2015)].We developed a constitutive model for large-scale analysis of steel building frames,and its prototype has been successfully used in a detailed and large-scale simulation of a steel frame discretized into solid elements of about 19 million degrees of freedom[?Miyamura,Yamashita,Akiba,Ohsaki(2015)].In this paper,we present the details of the constitutive model.In the field of mechanical engineering and material science,various constitutive models,including Armstrong-Frederic(AF)model[Armstrong and Frederick(1966)],multi-layer model[Besseling(1958)],and bounding surface model[Dafarias and Popov(1975)],have been developed for simulating cyclic elastoplastic behavior of various types of steel materials.By contrast,in the field of civil engineering,rolled mild steel materials are widely used.One of the important and distinct properties of these materials is the existence of a sharp yield plateau,which leads to different characteristics between the first and subsequent loadings[Ucak and T-sopelas(2011);Rodzik(1999)].Yoshida(2000)developed a viscoplastic model for simulation of cyclic responses of a material exhibiting yield plateau.Yoshida and Uemori(2002)and Shen,Tanaka,Mizuno,Usami(1992)presented constitutive models using combined isotropic-kinematic hardening and bounding surfaces for simulation of Bauschinger effect.However,they did not explicitly distinguish the first and subsequent loadings.Recently,Ucak and Tsopelas(2011)developed a cyclic model that can simulate yield plateau using the AF model and a bounding surface.

Ohno and Wang(1993)proposed an evolution rule of backstress for accurate simulation of dynamic recovery and ratcheting behavior,and derived the consistent tangent operator for implementation to a finite element analysis code[Kobayashi and Ohno(2002)].In contrast to complex evolution rules,for which derivation of consistent tangent operators is complicated[Mühlich and Brocks(2003);Diegele,Jansohn,Tsakmakis(2000)],linear isotropic-kinematic hardening model has a very stable algorithm of consistent tangent based on analytical solution of consistency condition[Kossa and Szabó(2009);Auricchio and sa Veiga(2003);Romashchenko,Lepikhin,Ivashchenko(1999)].Therefore,our constitutive model based on linear hardening can be applied to a large-scale simulation of steel structures.

Most of the existing studies on constitutive models of steel materials are intended to developexplicitevolution rules of stresses and strains in reference to the physical behavior of the material idealized as a continuum.There is another direction of research for developing animplicitconstitutive relation,which is not defined based on an explicit differential equations of stresses,strains,and internal variables,but instead,defined in a heuristic and algorithmic manner.For example,Furukawa and Yagawa(1998)used a neural network for modeling implicit constitutive relation of a visco-elastoplastic material subjected to uniaxial cyclic loading.However,a completely implicit relation between the stress rates and strain rates cannot be obtained generally for multiaxial loading,because such relation depends on the loading history.Note that the terms explicit and implicit are not related to those for solution algorithm of differential equations as discussed in[Ellsiepen and Hartmann(2001)].In the field of civil engineering,there are many macro(phenomenologicalorphysical)models such as plastic hinges and fiber models for simulating cyclic plastic behavior of beams,columns,and braces[Uriz,Filippou,Mahin(2001);Kim and Lee(2001);Ishizawa and Iura(2006)].Composite beam elements have also been developed[Bradford and Pi(2012)].

In this paper,an intermediate implicit and explicit model,calledsemi-implicit model,is presented for rolled mild steel materials.The purpose of this paper is summarized as follows:

1.Present a simple constitutive model for cyclic behavior of steel material used for civil engineering exhibiting yield plateau and Bauschinger effect.

2.Present an algorithm that can be used for finite element analysis with solid elements.

3.Present an optimization algorithm for identification of material parameters.

The constitutive relation is defined in an algorithmic manner based on the piecewise linear combined isotropic-kinematic hardening.Different rules are used for the first and subsequent loading states.We also present an efficient optimization method,based on a heuristic approach called tabu search(TS)[Glover(1989);Ohsaki(2010)],for parameter identification from the material test results.The accuracy of the constitutive model is discussed in examples of a cantilever subjected to symmetric and asymmetric cyclic loads.

2 Overview of J2plasticity

In this section,we summarize the basic equations of J2-plasticity for completeness of the paper.

Let σ and ε denote the stress and strain tensors,respectively.In the elastic range,the relation between σ and ε is defined by the linear elastic isotropic constitutive tensor CEas

Let s and e denote their deviatoric components;i.e.,

where‖·‖is the norm of a tensor.

We use the von Mises type(J2)yield criterion.The deviatoric components of backstress tensor,which defines the center of yield surface,is denoted as α .Thus the relative stress ξ is given as

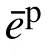
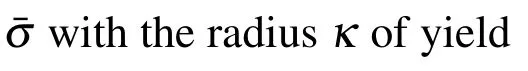
where n is the unit normal vector of the yield surface defined as

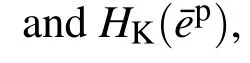
where κ0is the initial value of κ .The evolution rules for isotropic hardening and kinematic hardening are defined as

where(·)0denotes differentiation with respect to the equivalent plastic strain.

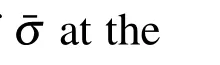
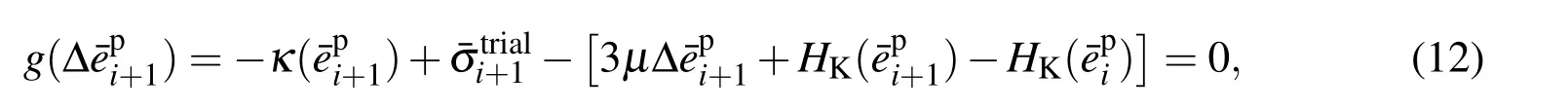
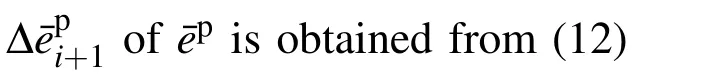
3 Piecewise linear semi-implicit constitutive model

3.1 Semi-implicit constitutive model

A steel material is intrinsically a polycrystal material,and continuum model is an approximation of a complex discrete behavior.Therefore,it is difficult to describe all properties of complex behavior explicitly using differential equations.

They trained the network using a numerical simulation of an existing explicit rule with a specified strain rate in the uniaxial deformation.Therefore,the model is effective for uniaxial model.

For a rate independent plasticity problem in multi-axial stress state,it may not be possible to develop a completely implicit model considering all possible states of the variables and all cases of loading/unloading conditions.Therefore,it is natural to utilize reliable hardening rules defined by differential equations.

An intermediate approach that is a combination of the explicit and implicit rules can be constructed,i.e.,some variables are updated explicitly and the others are updated implicitly.This approach is called a semi-implicit constitutive model.In the present paper,a semi-implicit constitutive model for a rate independent plasticity problem is proposed.It is based on the conventional explicit constitutive model using the piecewise linear isotropic and kinematic hardening rules with J2flow rules.The explicit constitutive model is extended to the semi-implicit one by introducing several implicit rules depending on internal variables such as the maximum equivalent stress experienced so far,equivalent plastic strain at the previous unloading point,etc.,which are represented by a vector a.Then,the semi-implicit rule is written as

This rule is based on the explicit isotropic-kinematic hardening rule,and variables in the vector a are updated using implicit or algorithmic rules.Note that other existing explicit constitutive models such as AF model[Armstrong and Frederick(1966)]and Ohno-Wang model[Ohno and Wang(1993)]have parameters that can be regarded as state variables with implicit update rules;i.e.,the parameters defining the size of the surface of critical state of Ohno-Wang model and the ratio of dynamic recovery of AF model can be included in the vector a as internal variables.

3.2 Implicit modeling of isotropic-kinematic hardening

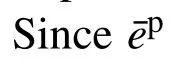
Let coefficients cIand cKdenote the ratios of the isotropic and kinematic hardening effects,respectively,satisfying

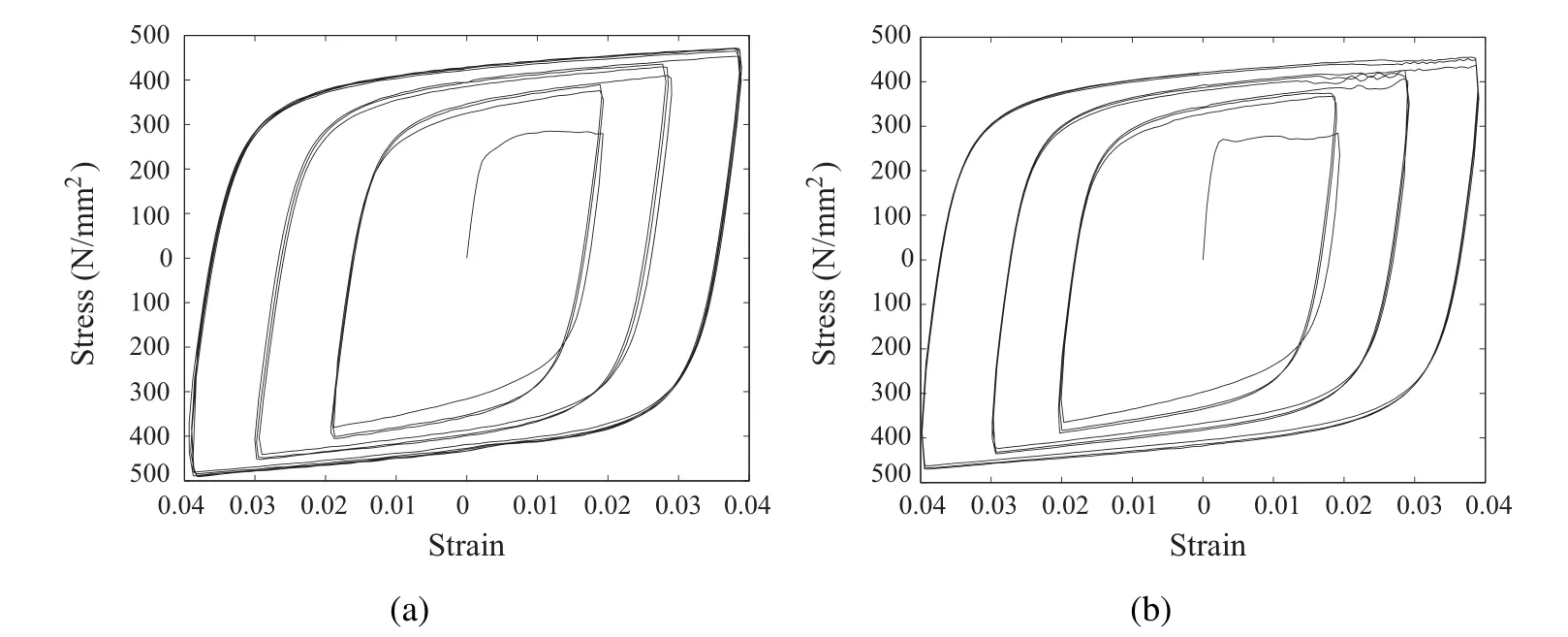
Figure 1:Uniaxial cyclic stress-strain relations of two typical steel materials in civil engineering;(a)SN400,(b)SS400[Yamada,Imaeda,Okada(2002)].

1.There exists a wide yield plateau,especially for SS400,in the first plastification(initial yielding);however,no clear yield plateau exists in the subsequent plastifications.

2.Yielding in the second plastic loading(first compressive plastification at‘C’in Fig.2)occurs at a smaller absolute value of stress than the first tensile loading(‘A’)due to Bauschinger effect.Furthermore,the difference between the stresses at first unloading(‘B’)and second loading(‘C’)is smaller than twice of the initial yield stress at ‘A’;however,the yield stress gradually increases in the subsequent loading cycles due to isotropic hardening.

3.The stress-strain curves converge to the same loop within a constant range of specified strain;i.e.,the material yields at almost the same stress,implying that cyclic isotropic hardening effect is insignificant for this material.Note that the proposed constitutive model can be modified if cyclic hardening with constant magnitude of strain is not negligible.

From the observations of the physical tests,we need at least two types of stressstrain curves,as shown in Fig.2,to accurately describe the properties of the rolled mild steel materials;one for the first plastic loading with a yield plateau and the other for the subsequent plastic loading without yield plateau with smooth curvature.

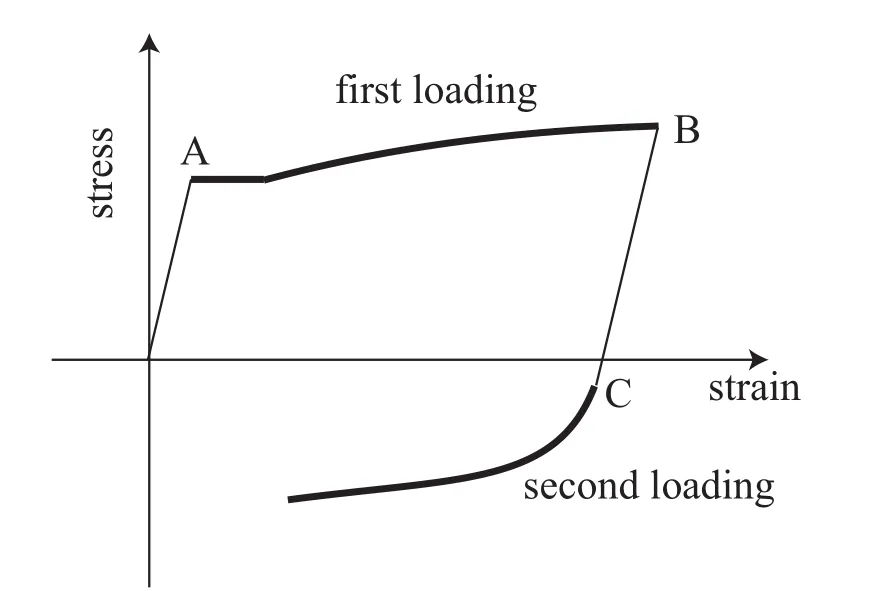
Figure 2:Illustration of two different plastic loading states in uniaxial cyclic loading.

Moreover,as observed in the experimental results,isotropic hardening and kinematic hardening have different coefficients in different loading states.Therefore,the following heuristic and implicit rules are proposed:

1.In the first plastic loading,we use an artificial negative value of the ratio cIfor isotropic hardening with positive H0to simulate the shrinkage of the yield surface as illustrated in Fig.3.

2.For the subsequent plastic loadings,we have to consider two cases based on the equivalent stressˆσ and the maximum valueˆσmaxexperienced in the preceding loading history:

The contribution of yield plateau and Bauschinger effect can be simulated using the AF model,where the back stress α is decomposed to m components as

The evolution of αiis defined as

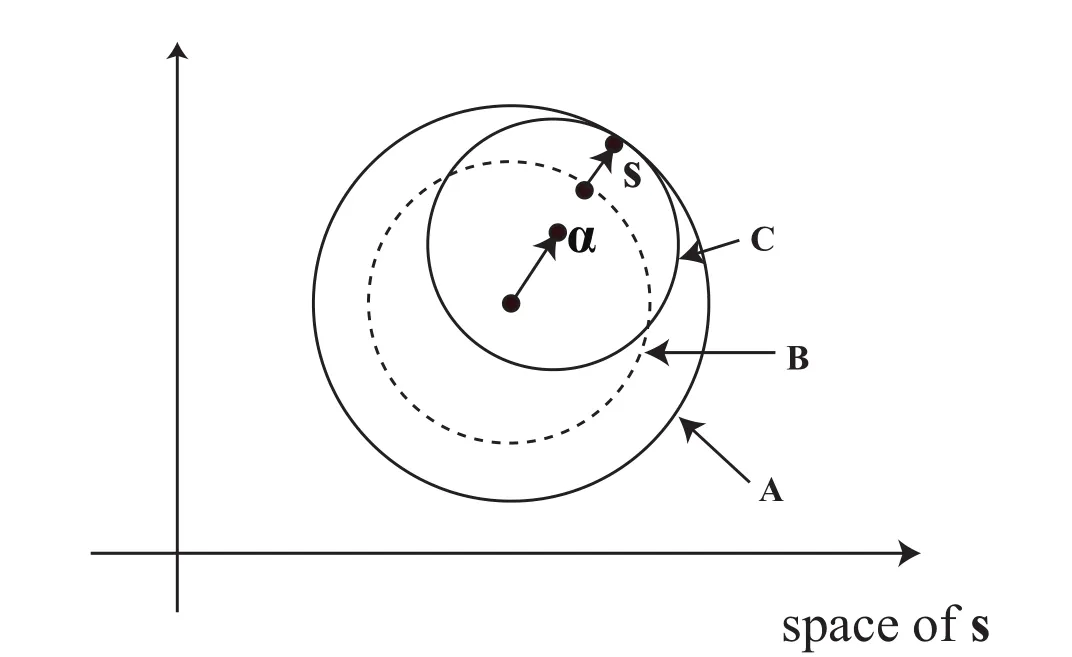
Figure 3:Illustration of artificial shrinkage of yield surface;circle A:true initial yield surface,circle B:artificial initial yield surface that is a little smaller than the true one,circle C:yield surface with small radius κ and nonzero backstress.

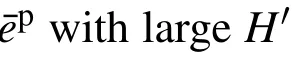
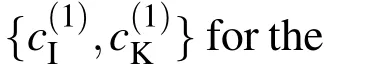
3.3 Radial return mapping

In the proposed semi-implicit constitutive model,a set of piecewise constant values are used forH0in(20).Suppose the computation has converged at theith incremental step of analysis.The radial return mapping algorithm for updating stresses and plastic strains at an integration point at the(i+1)th step of analysis,with the given increment Δε i+1of stain,is summarized in Algorithm 1 below.Procedures for updating the parameters for the semi-implicit constitutive model are also shown in the algorithm.

Algorithm 1:Radial return mapping

Step 1:Elastic predictor

Compute the trial stress as

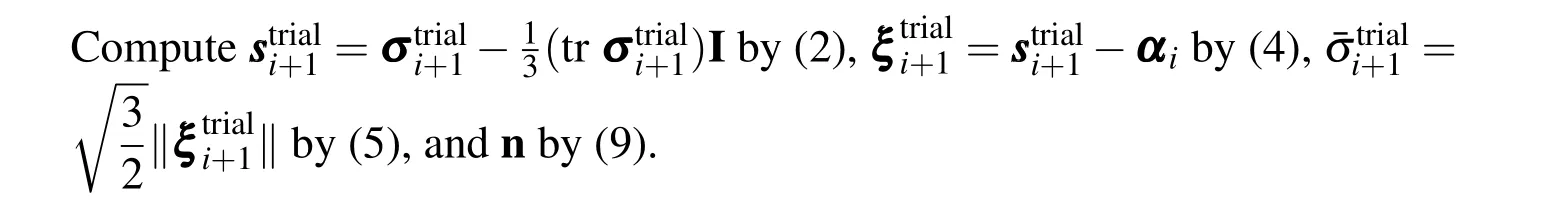
Step 2:Plastic corrector

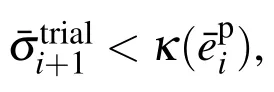
Furthermore,if the material is in plastic state at theith step,then elastic unloading occurs,and we record the previous equivalent plastic strain as

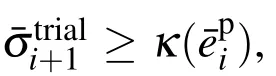
1.First plastic loading(curve 1):

2.Subsequent loading:

Step 3:State updater

If the stresses obtained from Algorithm 1 satisfy the equilibrium equations at each node,then the(i+1)th step of the analysis converges;otherwise,calculate a new increment of strain by considering the unbalanced forces and apply the algorithm again.

Figure 4:Stress-strain curve under asymmetric uniaxial cyclic loading.

3.4 Response to asymmetric cyclic loading

It is well known that simulation of responses to asymmetric cyclic loading is more difficult than that to symmetric loading.Fig.4 illustrates a stress-strain relation of an asymmetric uniaxial cyclic loading.The solid lines are the correct stress-strain relations,while the dashed lines are the‘wrong’relations due to improper modeling of hardening effect:

·In the process of reloading after no plastic loading in the opposite direction,the stress-strain path returns onto the extension of the stress-strain curve experienced in the previous plastic loading.Thus,after unloading at‘A’in Fig.4 and reversal of direction at‘B’,the stress-strain curve returns to ‘A’,and follows the original curve to ‘D’.Hence,curve ‘AC’shown in dashed line is inappropriate.

·When plastification occurs after unloading at‘E’,plastic strain accumulates between ‘F’and ‘G’,and the stress-strain hysteresis loops are open so that they resemble a creep effect under a large number of plastic loading cycles[Chaboche(2008)].Thus,the reloading occurs at‘I’that is a different point from the unloading point ‘E’,and stress-strain relation follows curve ‘IJ’which is different from the original curve.However,if the plastic deformation between ‘F’and ‘G’is small,the stress-strain path returns onto the original curve,i.e.,it follows the curve ‘IEK’.

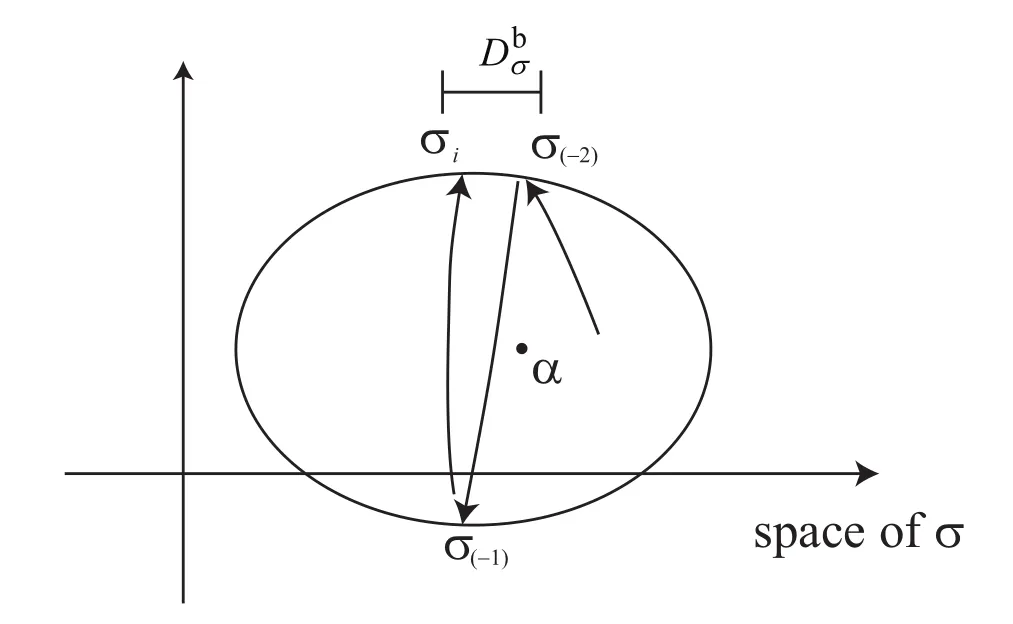
Figure 5:History of stress under cyclic loading.

To simulate responses against asymmetric cyclic loading,the following Algorithm 2 is added at the end of Case 2 in Step 2 of Algorithm 1:

Algorithm 2:Simulation of responses to asymmetric loading

If the material is currently in plastic state,then consider the following two cases:

1.If the material is in elastic state at the previous step,and the norm of difference between the current stressσ iand the stressσ(-1)at the previous unloading point is smaller than a specified small positive valueDaσ;i.e.,

then reloading occurs without plastic loading in the opposite direction;hence,we set

and update

so as to follow the curve of the previous plastic loading as illustrated as the path A→B→A→D in Fig.4.

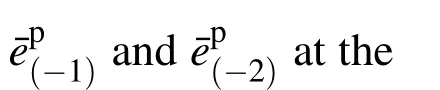
and the difference between the current stressσ iand the stressσ(-2)at the second previous unloading points is smaller than a specified small valueDbσ,as illustrated in Fig.5;i.e.,

then the plastification in the opposite direction is negligibly small.Therefore,we set

and update

so as to follow the previous plastic loading curve.

According to Algorithm 2,the yield plateau does not appear at reloading after unloading from the plateau even if the equivalent plastic strain is very small.However,as noted in Ucak and Tsopelas(2011)and Rodzik(1999),the yield plateau remains if the equivalent plastic strain is small enough.Therefore,the following rule is added:

Algorithm 3:Simulation of unloading from yield plateau

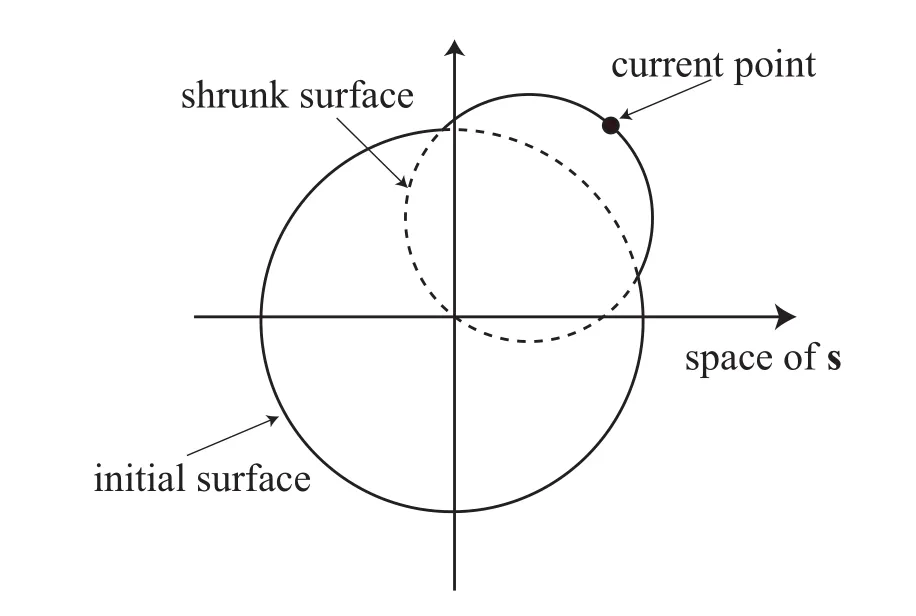
Figure 6:Illustration of union of initial yield surface and shrunk surface.

However,the size of yield surface has been shrunk after first yielding.Therefore,the stress of reloading at the yield surface is smaller than the real value after slightly experiencing plastic deformation in opposite direction.To prevent this unrealistic situation,we use the union of initial and shrunk surfaces as the yield surface as illustrated in Fig.6 until¯epexceeds¯eYP.

In the following applications,Algorithms 1-3 are implemented in the material library of the E-Simulator.The accuracy and stability of the algorithms have been confirmed through various numerical experiments including the seismic response analysis of a model with about 19 million degrees of freedom[?Miyamura,Yamashita,Akiba,Ohsaki(2015)].

4 Parameter identification from material test

This section proposes an identification method for the parameters of the semiimplicit constitutive model using results of cyclic uniaxial material tests.The parameters to be identified,which are the variables of an optimization problem,include the initial yield stress,the hardening coefficients of the piecewise linear stress-strain curves,and the ratios of isotropic-kinematic hardening.The square error between analysis and experiment results is minimized to find the optimal parameter values.

4.1 Problem description

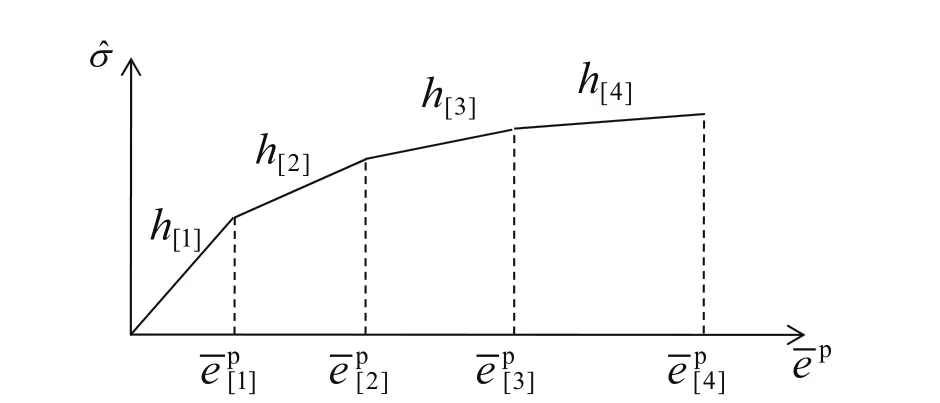
Figure 7:Piecewise linear relation between equivalent plastic strain and equivalent stress for a monotonic loading with constant hardening coefficient h[i]in the ith interval.

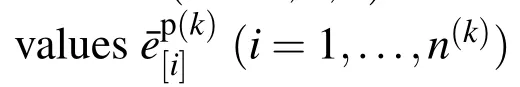
which are represented by a vector x.Note that the elastic modulus is identified from the initial stiffness only.Fixed values are assigned for Daσ,Dbσ,and D¯ep.

where the summation is carried out in the set of stepsPin plastic loading state.

Constraints are given,as follows,so that the hardening coefficient is anon-increasing function of the equivalent plastic strain:

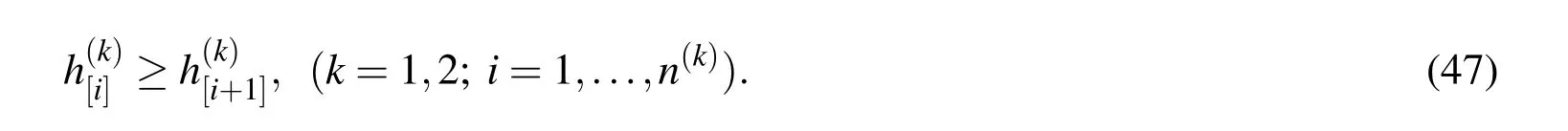
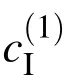
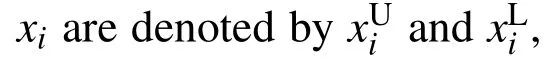
Each variable is discretized intosequally spaced valuesxij(j=1,...,s)as

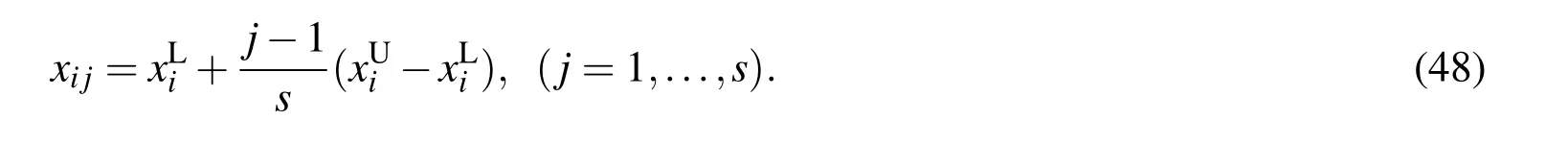
The algorithm of TS is summarized as follows:

Step 1Assign an initial seed solution forx,and initialize the tabu listTto be empty.

Step 2Generate neighborhood solutions of the current seed solution and move to the best feasible solutionx∗among them that is not included in the listT.

Step 3Addx∗toT.Remove the oldest solution inTif the length of the list exceeds the specified limit.

Step 4Acceptx∗as the next seed solution and go to Step 2 if the number of steps is less than the specified limit;otherwise,output the best solution and terminate the process.

The neighborhood solutions are generated using a random numberτ∈[0,1].Each variable is increased by 1 ifτ≥2/3,decreased by 1 ifτ＜1/3,and is not modified if 1/3≤τ＜2/3.

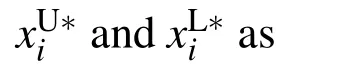
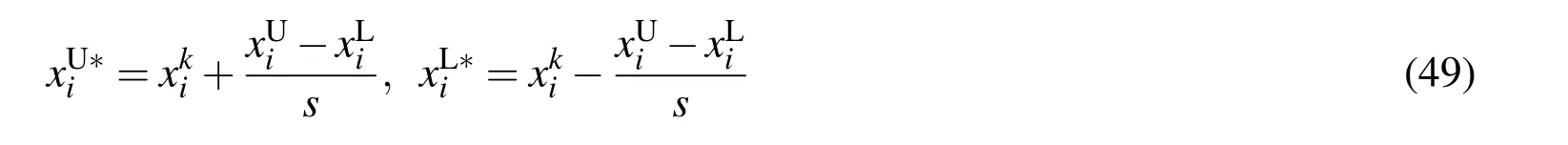
Each parameter is discretized again into s integer values in a similar manner as(48),and TS is carried out again from several different random seeds.

4.2 Parameter identification using cyclic test

In the following,the units of length and force are mm and N,respectively.The parameters are identified from the uniaxial cyclic material test of SS400[Yamada,Imaeda,Okada(2002)]as shown in Fig.1(b).We cannot identify the hardening coefficients beyond yield plateau of curve 1,because the first unloading occurs from the yield plateau in Fig.1(b).Furthermore,we fix the hardening coefficient at yield plateau,and only the hardening coefficient in the small interval at the first yielding is considered as variable;i.e,n1in(45)is 1.The number of intervals in the subsequent stress-strain relation is seven;i.e.,n2=7 in(45).We have twelve variables in total including σ0y,c(1)I,c(2)I,and c(3)I.

Optimization using TS is carried out for identification of parameters.Values of the fixed parameters are set as

·Elastic modulus:1.7505×105N/mm2

·Poisson’s ratio:0.3

·Equivalent plastic strains at the boundaries of intervals:

The variables are discretized into s=20 values.The numbers of neighborhood solutions and total steps for TS are 12 and 50,respectively.The length of tabu list is large enough so that each solution is selected only once.TS is carried out from five different initial random seeds to find five approximate solutions.Parameters are re-discretized to 20 values around each approximate solution,and TS is carried out again from five different random seeds.The five approximate solutions,denoted by Optk(k=1,...,5),obtained as the best solution after the second step are listed in Tab.2.

Table 1:Bounds of parameters.

Among five solutions,Opt 3 has the smallest value ofE(x),and its stress-strain relation is plotted in dotted line in Fig.8.The solid line shows the experimental result by Yamada,Imaeda,Okada(2002).As seen from the figure,the numerical results have high accuracy of simulating cyclic uniaxial loading of the steel material.

The results for flange and web are listed in Tab.3.The monotonic stress-strain relation for flange and web are plotted in Figs.9(a)and(b),respectively,where solid lines are the experimental results,and dotted lines are the numerical results corresponding to Opt 2-1 for flange and Opt 2-5 for web.It can be observed from the figures that good approximation has been achieved.

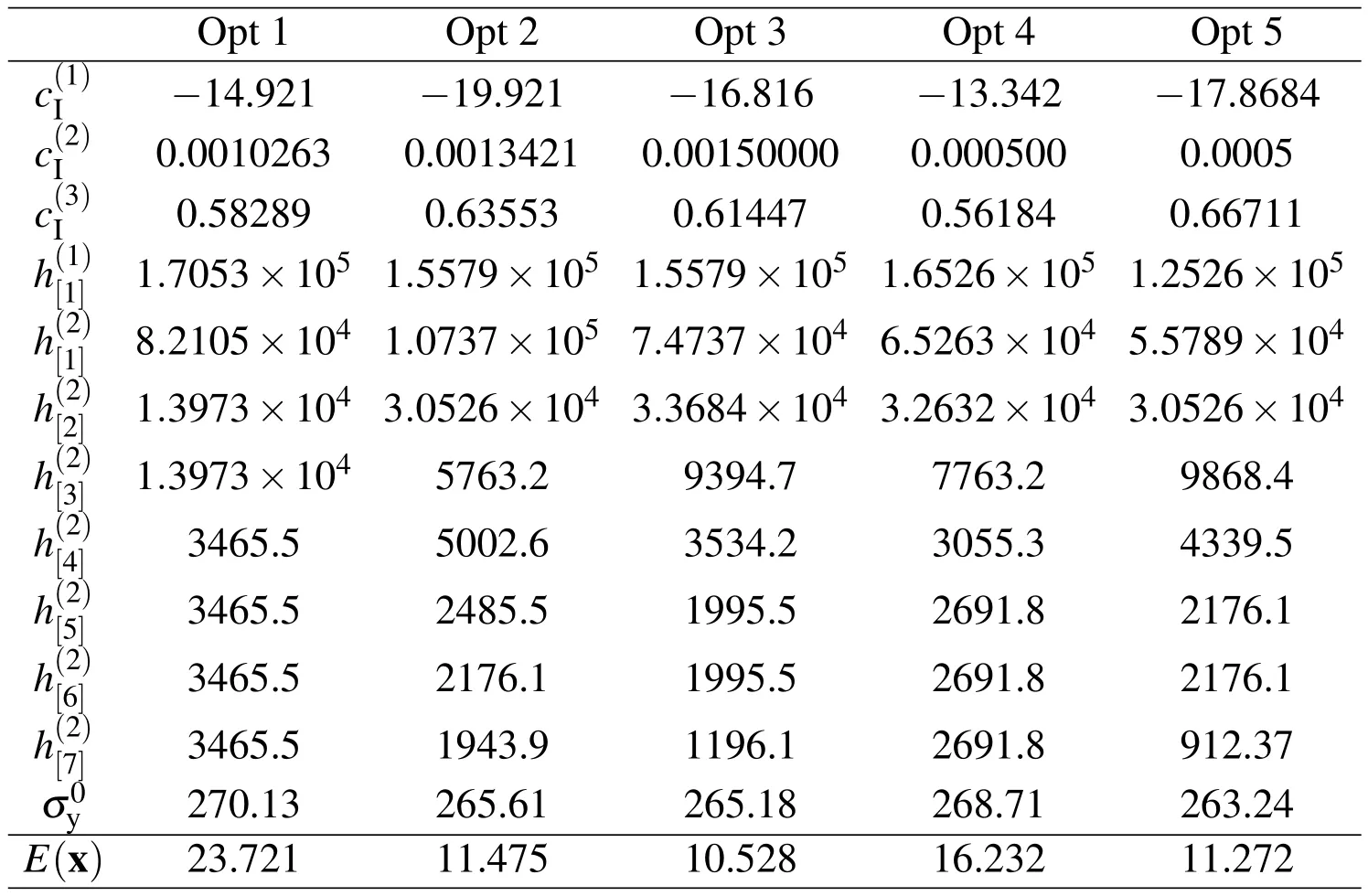
Table 2:Results of second step of parameter identification by TS.

5 Illustrative example and FE analysis of cantilever

We demonstrated in the previous section that the proposed semi-implicit constitutive model has high accuracy in simulation of cyclic uniaxial loading for rolled mild steel materials in civil engineering.In this section,we first demonstrate the necessity of implementation of Algorithms 2 and 3 in simulation of cyclic loading.Cyclic analysis is carried out for a cantilever as shown in Fig.10 as an example to show the accuracy of the proposed model used for structural analysis.

5.1 Cyclic analysis of single element

To illustrate the importance of implementation of Algorithms 2 and 3 for cyclic loading,we consider a simple example with only one hexahedral solid element.The parameters for Algorithms 2 and 3 are given as

·Small bounds for Algorithm 2:

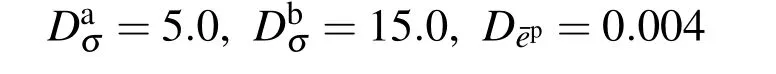
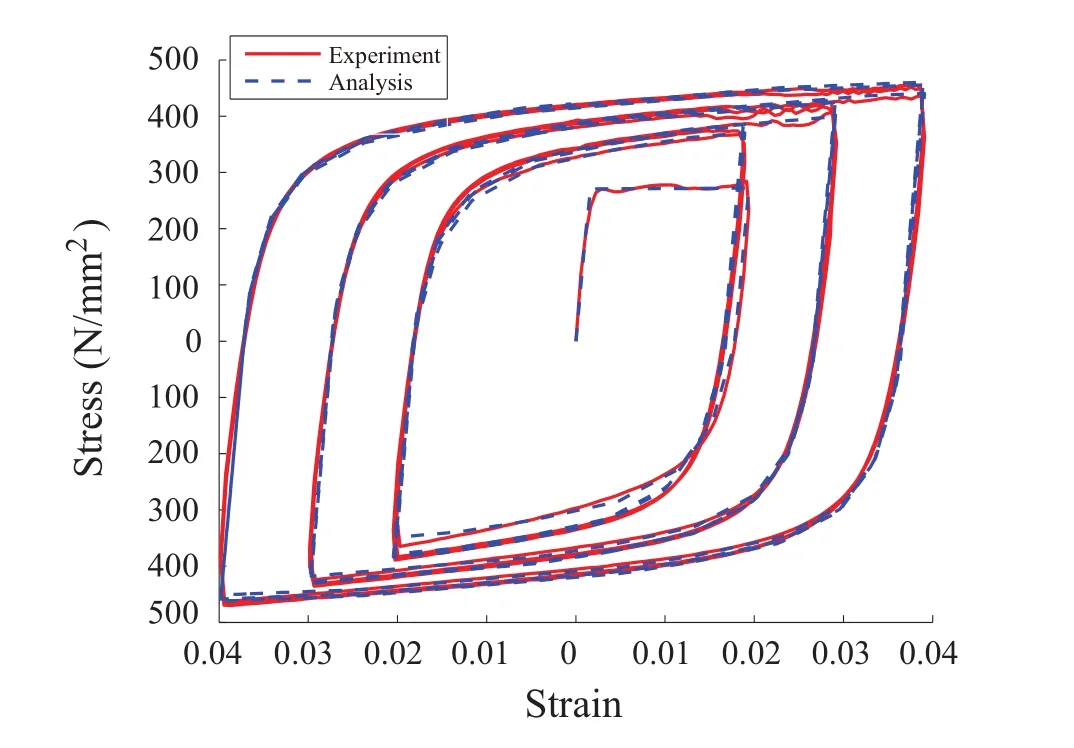
Figure 8:Stress-strain relation of for the cyclic uniaxial material test of SS400 using the identified parameter values.

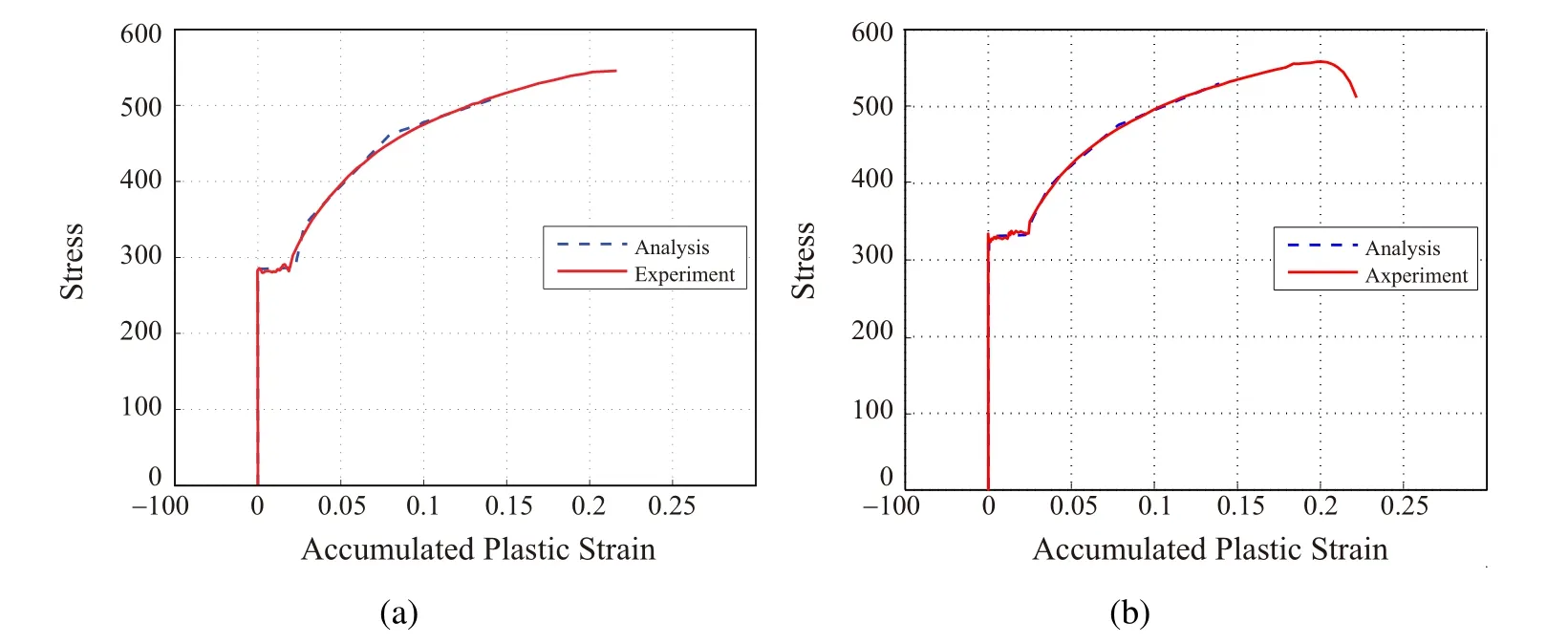
Figure 9:Stress-strain curves for flange and web after identification of hardening coefficients and yield stresses from uniaxial material test,corresponding to Opt 3;(a)flange,(b)web.

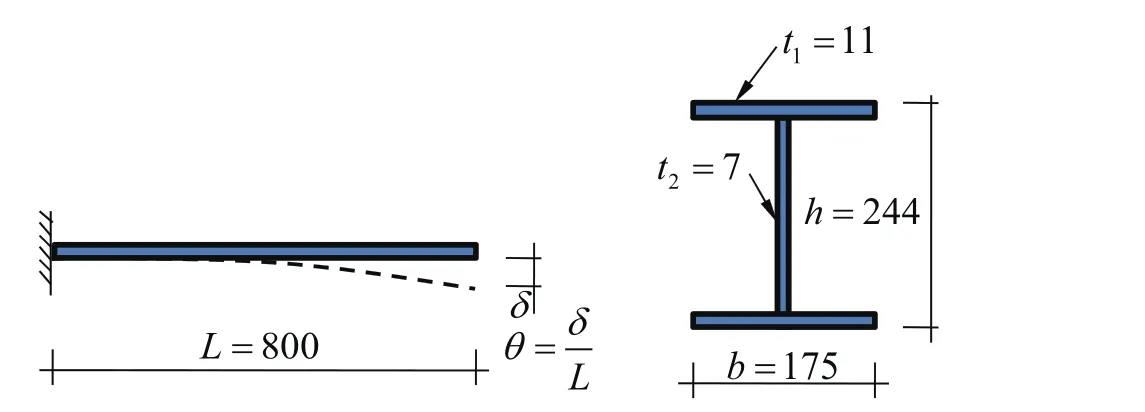
Figure 10:Geometry of cantilever and its cross-section;(Unit:mm).

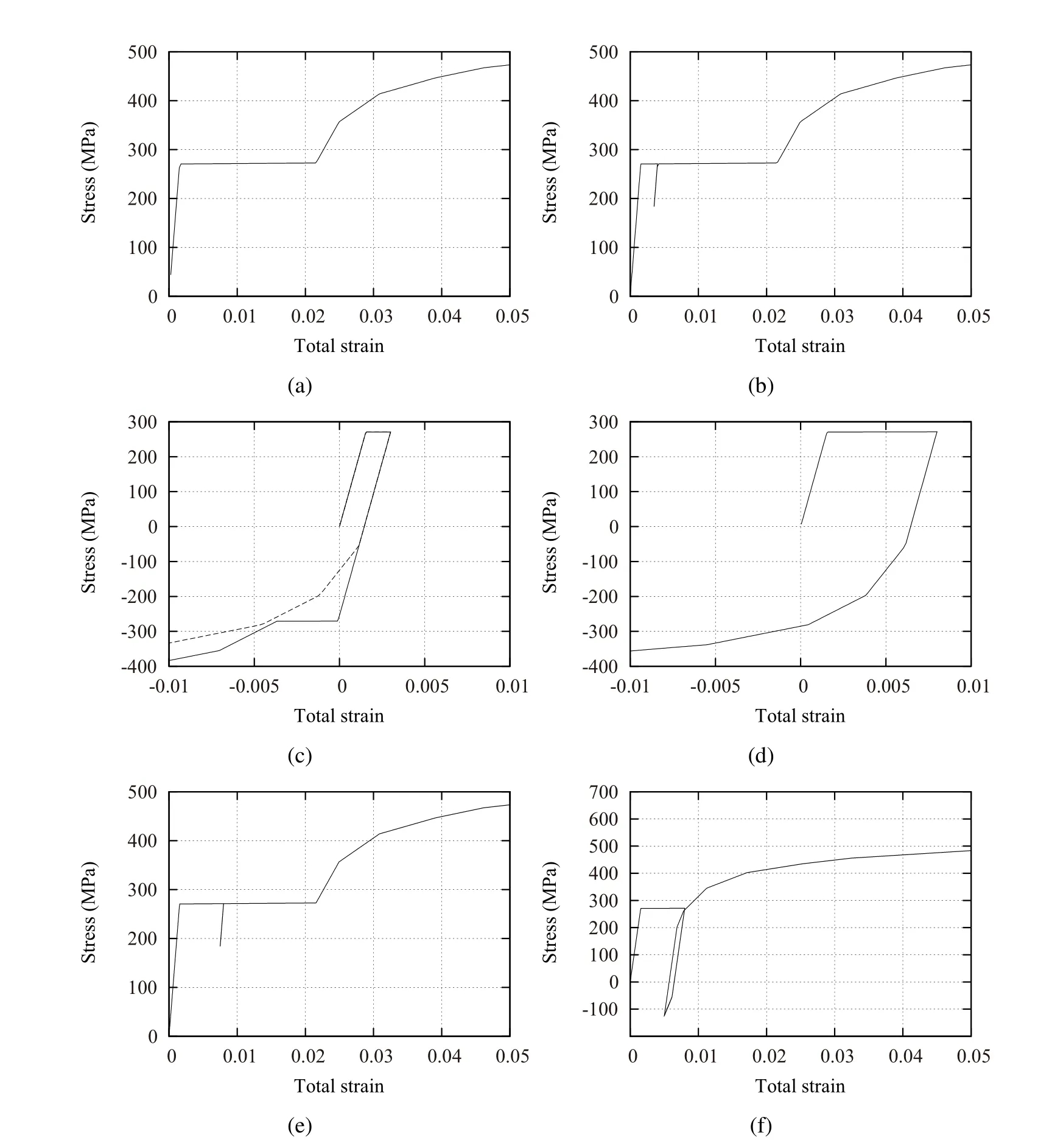
Figure 11:Cyclic behavior with reloading from yield plateau;(a)monotonic loading,(b)reloading without loading in the opposite direction,(c)reloading at small equivalent plastic strain after loading in the opposite direction,(d)reloading at large equivalent plastic strain after loading in the opposite direction,(e)reloading at large equivalent plastic strain without loading in the opposite direction,(f)reloading at large equivalent plastic strain after slight loading in the opposite direction.

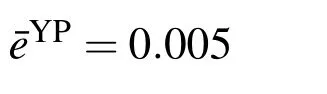
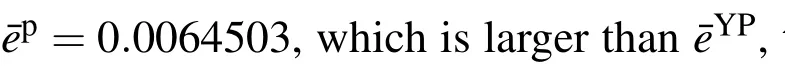
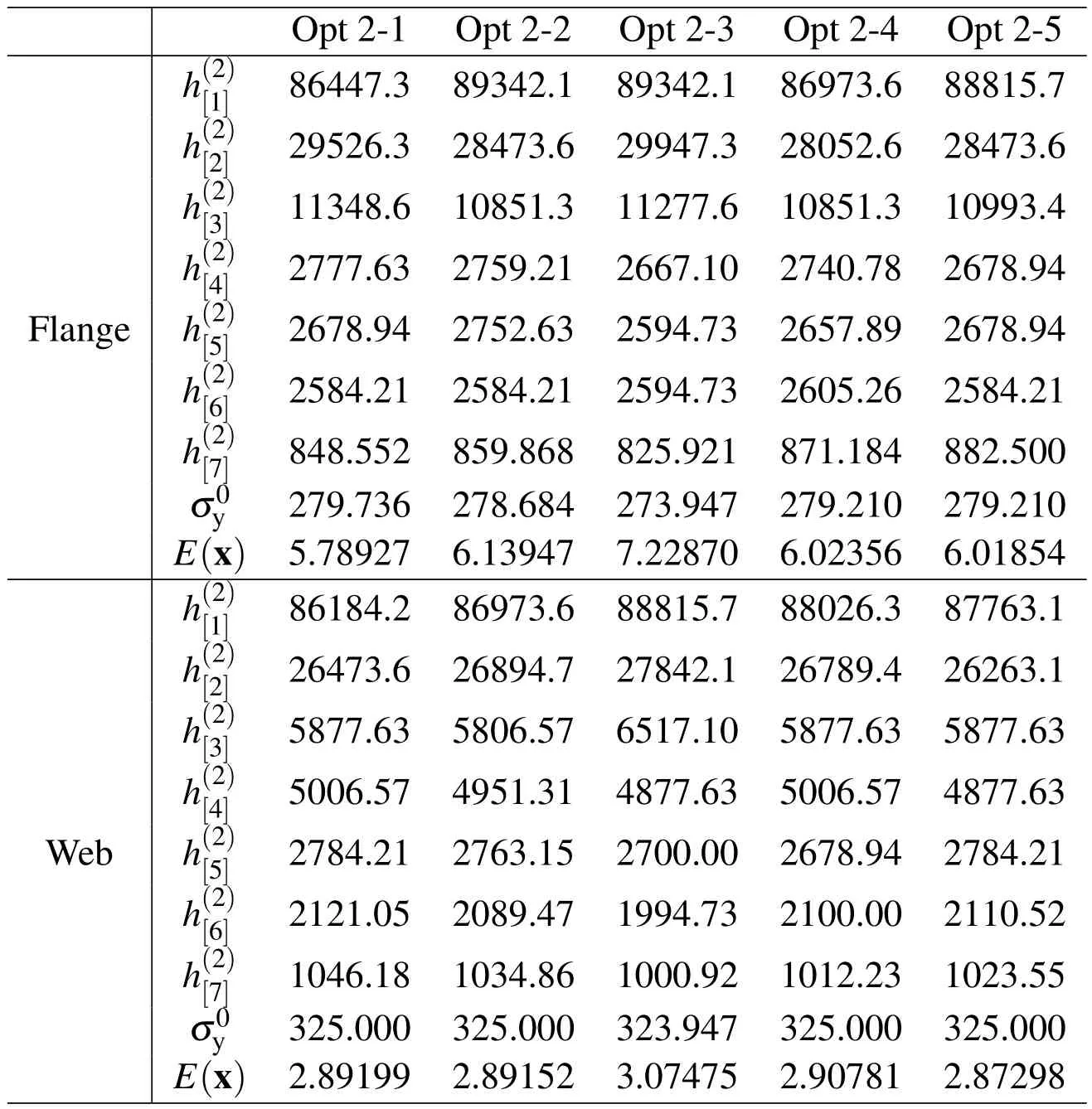
Table 3:Results of parameter identification of curve 2 and yield stress of flange and web using monotonic uniaxial tests.

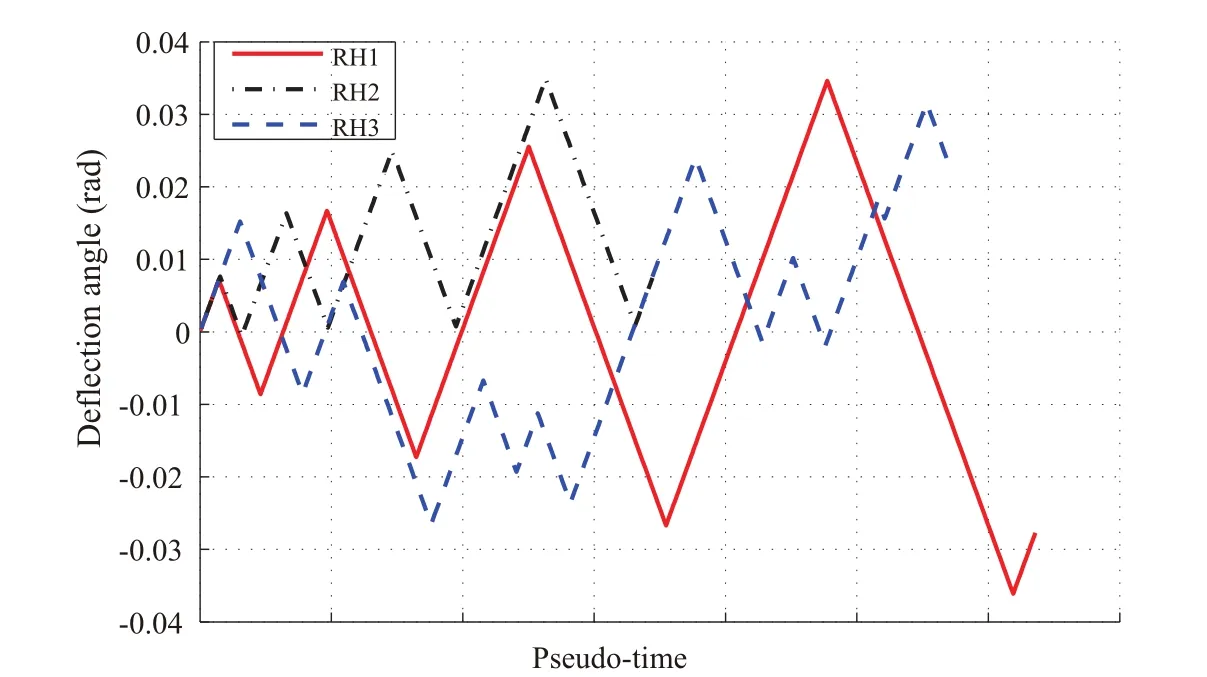
Figure 12:Loading patterns for the cantilever.

5.2 Cyclic analysis of cantilever

To demonstrate the effectiveness of the proposed constitutive model for analysis of structures in building engineering,we carry out elastoplastic cyclic analysis of a cantilever consisting of rolled wide-flange section H-244×175×7×11 as shown in Fig.10.The web and flange are made of the same material SS400 with different yield stresses.The left end of cantilever is clamped,and forced vertical displacement is given at the right end.The average deflection angle θ of the beam is defined by dividing the tip displacement δ by the beam length L=800 mm.

Yamada,Imaeda,Okada(2002)conducted physical experiments under three different loading patterns RH1,RH2,and RH3 described in terms of deflection angles as shown in Fig.12.The loading pattern RH1 is symmetric,RH2 gradually deflects in one direction,and RH3 is asymmetric.The cantilever is discretized using hexahedral finite elements with quadratic interpolation function.The flanges and web are divided into three layers as shown in Fig.13.Each element has 20 nodes,and the total numbers of elements and nodes are 2700 and 14167,respectively.Sufficiently small increment is used to simulate the history of complex behavior of the material using the semi-implicit constitutive model.The total number of incremental steps for the loading patterns RH1,RH2,and RH3 are 555,362,and 443,respectively.We use the parameter values identified in Sec.4.For the symmetric loading pattern RH1,the relation between the deflection angle and the bending moment at the fixed end is shown in Fig.14,where the solid and dotted lines,respectively,correspond to numerical and experimental results.The numerical analysis reproduces the behavior of the cantilever with good accuracy in the subsequent cycles,although the strength is slightly larger than the experimental result.

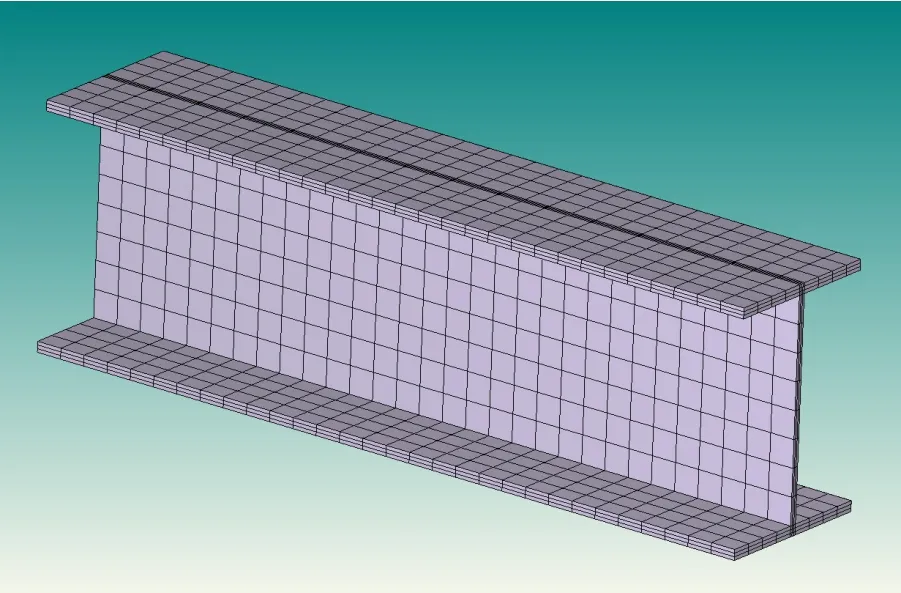
Figure 13:Finite element mesh of the cantilever.

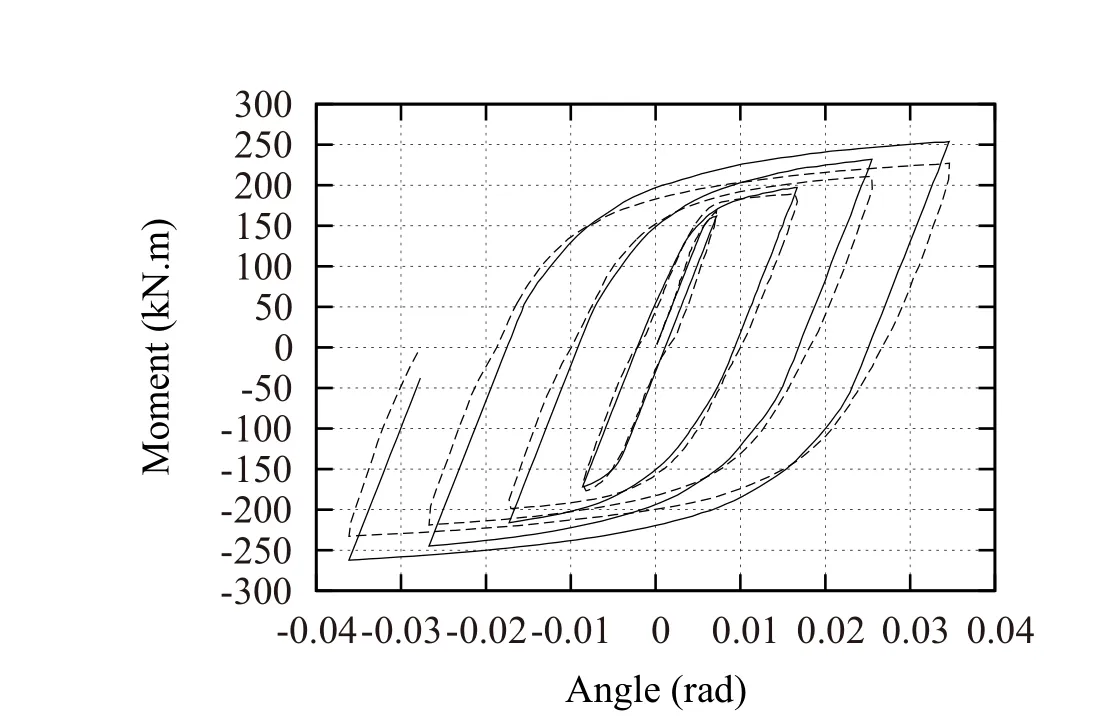
Figure 14:Relation between average deflection angle and bending moment for loading pattern RH1;solid line:analysis,dotted line:experiment.

For the more complex loading patterns RH2 and RH3,the numerical results together with the experimental results are respectively plotted in Figs.15(a)and(b).As seen from the figures,the responses evaluated using the proposed model has good accuracy for even these asymmetric loading patterns.It should be noted here that the constitutive parameters are identified using only the cyclic and monotonic material tests,and no tuning has been made in view of the results of cantilever subjected to three different loading conditions.

For comparison purpose,we also carried out numerical analysis for RH3 using simple isotropic and kinematic hardening rules,respectively,where the bilinear hardening models are used and the hardening coefficient is equal to 1/100 of the elastic modulus.The numerical results for the two cases are shown in Fig.16,also with the experimental results for reference.It is obvious from Figs.15(b)and 16 that the proposed constitutive model has much higher accuracy than simple isotropic or kinematic hardening model in simulation of behavior of the cantilever subjected to a symmetric cyclic loading.Obviously,the expansion of yield surface cannot be simulated by the kinematic hardening model,while the isotropic hardening cannot simulate the Bauschinger effect.

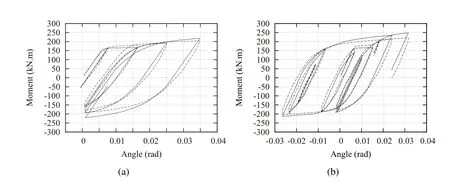
Figure 15:Results of asymmetric loading patterns;solid line:analysis,dotted line:experiment;(a)RH2,(b)RH3.

Figure 16:Results of simple hardening rules for loading pattern RH3;solid line:analysis,dotted line:experiment;(a)isotropic,(b)kinematic.

6 Conclusions

An intermediate implicit and explicit constitutive model,called semi-implicit model,has been proposed for the rate-independent elastoplastic constitutive models of rolled mild steel materials used in the field of civil engineering.The model simulates the behaviors of steel materials subjected to cyclic loading,while existence of yield plateau and Bauschinger effect is considered.

The constitutive model has been implemented in the E-Simulator,which is a software package for large-scale seismic response analysis and is currently underdevelopment at the National Research Institute of Earth Science and Disaster Prevention(NIED),Japan.The accuracy and stability of the prototype of the constitutive model have already been confirmed through various numerical experiments including the seismic response analysis of a model with about 19 million degrees of freedom.

The constitutive relation is defined in an algorithmic manner based on the piecewiselinear combined isotropic-kinematic hardening.Different rules are used for the first and subsequent loading states to consider the wide yield plateau in the first loading,and a rule is also included for simulating reloading after unloading from the yield plateau.Moreover,the Bauschinger effect is simulated by shrinkage of the yield surface using a negative ratio for isotropic hardening.

The conventional formulations of radial return mapping for predictor-corrector incremental algorithm and the consistent tangent stiffness proposed in[Simo and Taylor(1985)]can be used without any modification incorporating explicit solution of the consistency condition.Therefore,the proposed model can be implemented easily by simply adding the new hardening functions to an existing and reliable code,and very stable computation without divergence can be achieved in the framework of J2-plasticity.

An optimization approach using TS has been presented for identification of the constitutive parameters from uniaxial material tests.The ratio of isotropic hardening as well as the parameter values for modeling Bauschinger effect is identified from a cyclic material test.The hardening coefficient as function of plastic strain can be identified from uniaxial material test,if cyclic test is not available,utilizing the accumulated equivalent plastic strain under cyclic analysis.Hence,the proposed approach can be widely used in a practical situation,because cyclic test is much more difficult than monotonic test.

The accuracy of the model has been demonstrated through numerical examples of a cantilever subjected to three different types of cyclic loads.It has been shown that the elastoplastic responses under complex asymmetric cyclic loads can be simulated accurately using the proposed model without any specific tuning for the structural model;only material tests for identification of the parameters are needed for accurate estimation of elastoplastic cyclic responses.

Acknowledgement:This study is partly supported by E-Defense Seismic Experimental Research and Simulation System Construction Project at NIED conducted by E-Simulator Development Committee.The authors would like to show sincere appreciation to Prof.Satoshi Yamada of Tokyo Institute of Technology,Japan,who have provided us with the experimental results.The valuable contribution by Dr.Tomonobu Ohyama and Mr.Yusuke Narutomi of Allied Engineering Corporation,and Dr.Takuzo Yamashita of National Research Institute for Earth Science and Disaster Prevention is also acknowledged.

Allied Engineering(2015):ADVENTURECluster.http://www.alde.co.jp/.

Armstrong,P.J.;Frederick,C.O.(1966):A mathematical representation of the multiaxial Bauschinger effect,GEGB Report RD/B/N 731,Berkeley Nuclear Laboratories,Berkeley,CA.

Auricchio,F.;sa Veiga,L.B.(2003):On a new integration scheme for von-Mises plasticity with linear hardening,Int.J.Numer.Meth.Engng.,vol.56,pp.1375-1396.

Besseling,J.F.(1958):A theory of elastic,plastic and creep deformations of an initially isotropic material showing anisotropic strain hardening,creep recovery and secondary creep,J.Appl.Mech.,ASME,vol.25,pp.529-536.

Bradford,M.A.;Pi,Y.L.(2012):Nonlinear elastic-plastic analysis of composite members of high-strength steel and geopolymer concrete,Computer Modeling in Engineering&Science,vol.89,no.5,pp.387-414.

Chaboche,J.L.(2008):A review of some plasticity and viscoplasticity constitutive theories.Int.J.Plasticity,vol.,pp.1642-1693.

Dafarias,Y.F.;Popov,E.P.(1975):A model of nonlinearly hardening materials for complex loading,Acta Mechanica,vol.21,pp.173-192.

Diegele,E.;Jansohn,W.;Tsakmakis,C.(2000):Finite deformation plasticity and viscoplasticity laws exhibiting nonlinear hardening rules,Comput.Mech.,vol.25,pp.1-12.

Ellsiepen,P.;Hartmann,S.(2001):Remarks on the interpretation of current non-linear finite element analyses as differential algebraic equations,Int.J.Numer.Meth.Engng.,vol.51,pp.679-707.

Furukawa,T.;Yagawa,G.(1998):Implicit constitutive modeling for viscoplasticity using neural network,Int.J.Numer.Meth.Engng.,vol.43,pp.195-219.

Glover,F.(1989):Tabu search:Part I,ORSA J.Computing,vol.1,pp.190-206.

Ishizawa,T;Iura,M.(2006):Analysis of partially concrete-filled steel tubular columns subjected to cyclic loadings,Computer Modeling in Engineering&Science,vol.11,no.3,pp.121-130.

Kim,S.E.;Lee,J.(2001):Improved refined plastic-hinge analysis accounting for local buckling,Eng.Struct.,vol.23,pp.1031-1042.

Kobayashi,M.;Ohno,N.(2002):Implementation of cyclic plasticity models based on a general form of kinematic hardening,Int.J.Numer.Meth.Engng.,vol.53,pp.2217-2238.

Kossa,A.;Szabó,L.(2009):Exact integration of the von Mises elastoplasticity model with combined linear isotropic-kinematic hardening,Int.J.Plasticity,vol.25,pp.1083-1106.

Miyamura,T.;Yamashita,T.;Akiba,H.;Ohsaki,M.(2015):Dynamic FE simulation of four-story steel frame modeled by solid elements and its validation using results of full-scale shake-table test,Earthquake Engng.Struct.Dyn.,DOI:10.1002/eqe.2526

Miyamura,T.;Ohsaki,M.;Kohiyama,M;Isobe,D;Onda,K.;Akiba,H.;Hori,M.;Kajiwara,K.;Ine,T.(2011):Large-scale FE analysis of steel building frames using E-Simulator,Progress in Nuclear Science and Technology,vol.2,pp.651-656.

Mühlich,U.;Brocks,W.(2003):On the numerical integration of a class of pressure-dependent plasticity models including kinematic hardening,Comput.Mech.,vol.31,pp.479-488.

Ohno,N.;Wang,J.D.(1993):Kinematic hardening rules with critical state of dynamic recovery:Part I,Formulation and basic features for ratchetting behavior,Int.J.Plasticity,vol.9,pp.375-390.

Ohsaki,M.(2010):Optimization of Finite Dimensional Structures,CRC Press.

Ohsaki,M.;Miyamura,T.;Kohiyama,M,;Hori,M.;Noguchi,H.;Akiba,H.;Kajiwara,K.;Ine,T.(2009):High-precision finite element analysis of elastoplastic dynamic responses of super-highrise steel frames,Earthquake Eng.Struct.Dyn.,vol.38,pp.635-654.

Rodzik,P.(1999):Cyclic hardening rule for structural steels with yield plateau,J.Eng.Mech.vol.125,no.12,pp.1331-1343.

Romashchenko,V.A.;Lepikhin,P.P.;Ivashchenko,K.B.(1999):Exact solution of problems of flow theory with isotropic-kinematic hardening,Part 1:Setting the loading trajectory in the space of stresses,Strength of Materials,vol.31,no.6,pp.582-591.

Shen,C.;Tanaka,Y.;Mizuno,E.;Usami,T.(1992):A two-surface model for steels with yield plateau,Structural Eng/Earthquake Eng.,Japan Society of Civil Engineers,vol.8,no.4,pp.179-188.

Simo,J.C.;Taylor,R.L.(1985):Consistent tangent operator for rate-independent elastoplasticity,Comp.Meth.Appl.Mech.Engng.,vol.48,pp.101-118.

Ucak,A.;Tsopelas,P.(2011):Constitutive model for cyclic response of structural steels with yield plateau,J.Struct.Eng.,vol.137,no.2,pp.195-206.

Uriz,P.;Filippou,F.C.;Mahin,S.A.(2008):Model for cyclic inelastic buckling of steel braces,J.Struct.Eng.,vol.134,no.4,pp.619-628.

Yamada,S.;Imaeda,T.;Okada,K.(2002):Simple hysteresis model of structural steel considering the Bauschinger effect,J.Struct.Constr.Eng.,Architectural Inst.of Japan,no.559,pp.225-232.(in Japanese)

Yoshida,F.(2000):A constitutive model of cyclic plasticity,Int.J.Plasticity,vol.16,pp.359-380.

Yoshida,F.;Uemori,T.(2002):A model of large-strain cyclic plasticity describing the Bauschinger effect and workhardening stagnation,Int.J.Plasticity,vol.18,pp.661-686.