A Homogenized Function to Recover Wave Source by Solving a Small Scale Linear System of Differencing Equations

Chein-Shan Liu,Wen Chen,Ji Lin

A Homogenized Function to Recover Wave Source by Solving a Small Scale Linear System of Differencing Equations

Chein-Shan Liu1,2,3,Wen Chen1,Ji Lin1

In order to recover unknown space-dependent function G(x)or unknown time-dependent function H(t)in the wave source F(x,t)=G(x)H(t),we develop a technique of homogenized function and differencing equations,which can significantly reduce the difficulty in the inverse wave source recovery problem,only needing to solve a few equations in the problem domain,since the initial condition/boundary conditions and a supplementary final time condition are satisfied automatically.As a consequence,the eigenfunctions are used to expand the trial solutions,and then a small scale linear system is solved to determine the expansion coefficients from the differencing equations.Because the ill-posedness of the inverse wave source problem is greatly reduced,the present method is accurate and stable against a large noise up to 50%,of which the numerical tests confirm the observation.

Wave source recovery problem,Eigenfunctions,Homogenized function,Differencing equations

1 Introduction

The wave motions are appeared in many engineering problems,for example the stress wave in solids,the wave propagation in fluids,the scattering problems of electromagnetic waves,and the sound wave propagation in media.There are many available methods for solving the wave equations of direct problems[Young and Ruan(2005);Shu,Wu,and Wang(2005);Godinho,Tadeu,and Amado Mendes(2007);Ma(2007);Young,Gu,and Fan(2009);Gu,Young,and Fan(2009);Kuo,Gu,Young,and Lin(2013);Dong,Alotaibi,Mohiuddine,and Atluri(2015)].

For a given wave propagation problem if one can find a solution satisfying both the governing equation and initial conditions/boundary conditions,then it is the exact solution of that problem.In general,it is very difficult to find the exact solution.In the numerical algorithm to solve the wave propagation problem,we can expand a trial solution by using the bases which automatically fulfil the governing equation but not necessary the initial conditions/boundary conditions.This sort method is known as the Trefftz method,including the method of fundamental solutions[Lin,Chen and Sun(2015)],and the method of wave polynomials[Maciag and Wauer(2005);Maciag(2005 2011)].Sometimes if the boundary conditions are homogeneous,one can use the eigenfunctions to expand the trial solution,where the eigenfunctions exactly satisfy the homogeneous boundary conditions.This inspires us to introduce the homogenized function,which renders the trial solution automatically satisfying the initial condition/boundary conditions and a measured supplementary condition at a final time.

For the hyperbolic systems there have been many works on the identifications of the point sources[Jang(2000);El Badia and Ha-Duong(2001);Komornik and Yamamoto(2002,2005);Ohe,Inui and Ohnaka(2011)].This study has an important application in the seismology detection,which could be regarded an approximation of elastic waves generated from point dislocation.The excitation force is assumed to have known time profile,and the problem is to determine the spatial variation from supplementary measurements.

The homogenized technique is used to find the unknown wave source in the following wave equation:

We intend to recover G(x)or H(t)in F(x,t)=G(x)H(t)under a supplementary condition measured at a final time t=tf,which may be polluted by noise:

where R(x)∈ [−1,1]is a random function.When the wave source only depends on x we set H(t)=1,and sometimes H(t)is given and we may need to estimate G(x)and the position of point sources.On the other hand,we may want to know the time varying wave source H(t),when G(x)is given.

2 A homogenized function method

Let

is a homogenized function.We can verify that

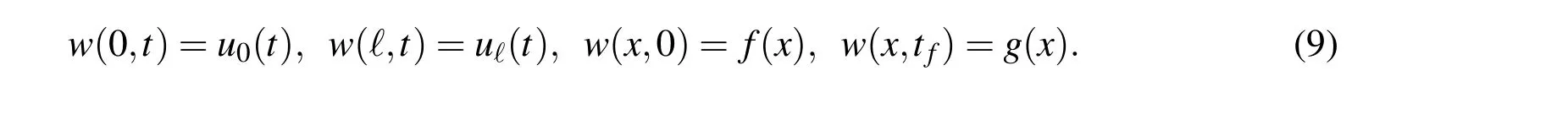
Inserting Eq.(7)into Eqs.(1)–(4)and(6)and using Eq.(9)we can derive

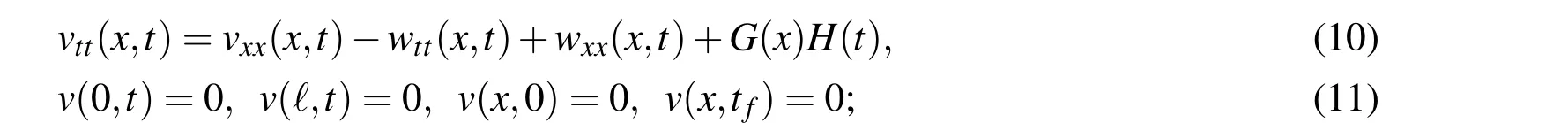
such that u given by Eq.(7)automatically satisfies the conditions(2)–(4)and(6).For this reason we call w(x,t)a homogenized function,which lends v(x,t)only subject to homogeneous initial/final/boundary conditions when we solve it by using Eq.(10).In view of Eq.(8)the homogenized function w(x,t)always exists,when Eqs.(2),(3),(4)and(6)are given.

We have transformed Eqs.(1)–(6)into Eqs.(10)and(11).Both are the inverse wave source recovery problems to find F(x,t)=G(x)H(t);however,Eqs.(10)and(11)are simpler than Eqs.(1)–(6).

We can expand v(x,t)and u(x,t)by using the eigenfunctions:

such that when v(x,t)automatically fulfills the homogeneous conditions in Eq.(11),u(x,t)automatically fulfills the conditions(2)–(4)and(6).Consequently,we may name the presented method the eigenfunction expansion method.

3 Collocation on lines along the space direction

The remaining problem is how to determine the coefficients cijin Eqs.(12)and(13).When cijare obtained,by Eq.(10)we can solve v(x,t);hence,G(x)is computed by

For the above purpose,the coefficients cijcan be arranged to be an n-dimensional vector c with components ck,k=1,...,n given by

To find the solution by using the eigenfunctions expansion method we must reduce the number of equations such that the condition number of the resultant linear system is greatly reduced.If we solve Eq.(10)we do not need to consider Eq.(11),because they are automatically fulfilled by the expansion of v in Eq.(12).

be a horizontal line inside Ω for each j=1,...,m2+1.At these m2+1 horizontal lines,Eq.(10)is satisfied:

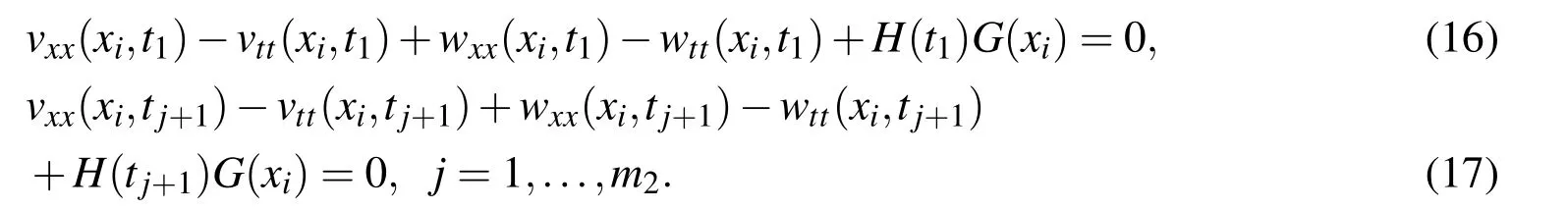
Multiplying Eq.(16)by H(tj+1)and Eq.(17)by H(t1)we have

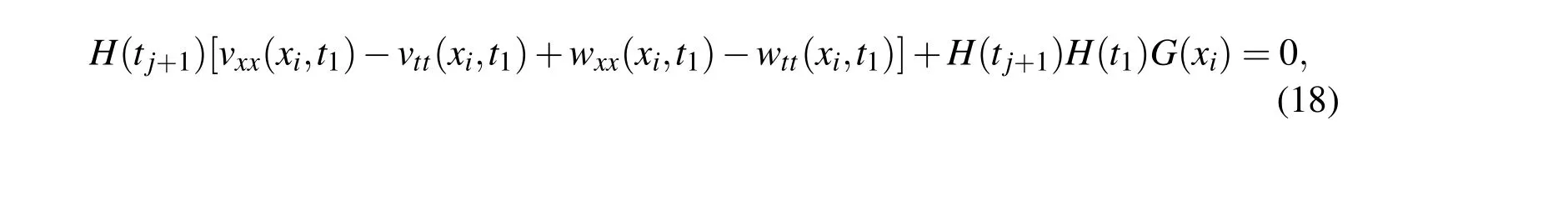
Subtracting Eq.(19)by Eq.(18),we can obtain

Then,by moving the terms about w into the right-hand side of Eq.(20),we have

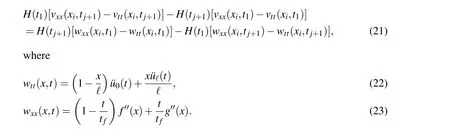
Because the unknown function G(x)is eliminated in Eq.(21),it can be simply used to solve v(x,t)by the collocation method,and then by using Eq.(14)to determine G(x).

By letting j run from 1 to m2in Eq.(21)and collocating points on t=0 to satisfy Eq.(5)we can derive a linear system:

where b presents the right-hand side of Eq.(21).Usually,Eq.(24)is an overdetermined system for that we may collocate more points to obtain more equations,which are used to find n coefficients in c with n＜nc.The dimension of A is nc×n,where nc=m1×m2.

Instead of Eq.(24),we can solve a normal linear system:

The algorithm of conjugate gradient method(CGM)for solving Eq.(25)is summarized as follows.

(i)Give an initial c0and then compute r0=Dc0−b1and set p0=r0.

(ii)For k=0,1,2,...,we repeat the following iterations:

If ck+1converges according to a given stopping criterion ‖rk+1‖ ＜ ε,then stop;otherwise,go to step(ii).

4 Numerical examples to recover G(x)

In this section we test the proposed methodology for the recovery of G(x)inF(x,t)=G(x)H(t)when H(t)/=0 is given.All the required boundary conditions initial condition and a supplementary condition can be derived from exact solution.Here we consider the noise being imposed on the measured data by

where R(i)are random numbers in[−1,1],and σ is the intensity of noise.

4.1 Example 1

In order to explore the applicability of the present method we consider

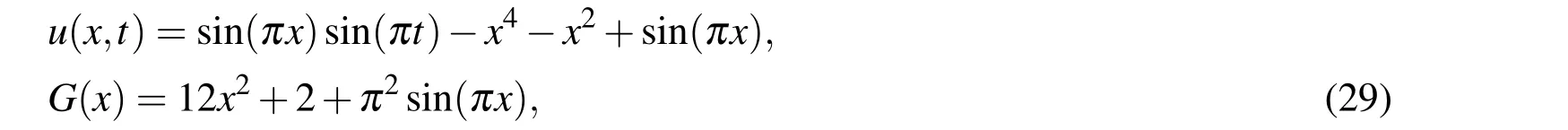
where H(t)=1.

In this case we take ℓ=4,tf=1,nc=600,and n=16.Under the convergence criterion ε=10−10the CGM is convergence with 34 steps.The noise is taken to be σ=0.5.InFig.1(a)we compare the numerically recovered and exact wave sources G(x),which can be seen very close,so that in Fig.1(b)we plot the numerical error.The maximum error of G(x)is 0.498.We can recover very well the unknown wave source in a large space range to ℓ=4,and under a large noise with σ =50%.

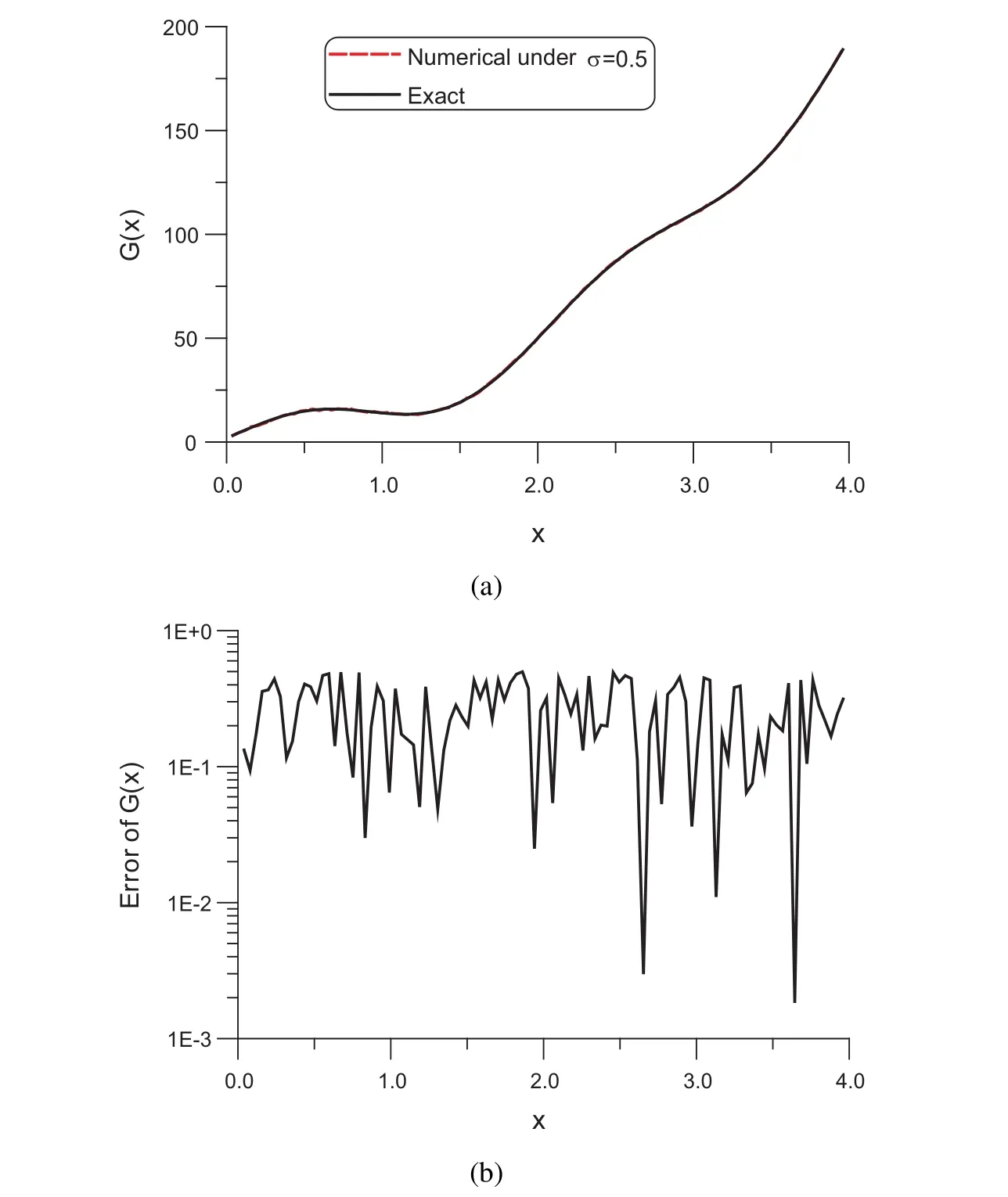
Figure 1:For the space-dependent wave source recovery problem of example 1,(a)comparing recovered and exact wave sources,(b)numerical error.

4.2 Example 2

Next,we consider a more complex inverse wave source problem with a bell shape function of G(x):

In this case we take ℓ=1,tf=1,nc=700,and n=9.Under the convergence criterion ε=10−10the CGM is convergence with 16 steps.We take σ =0.5.In Fig.2(a)we compare the numerically recovered and exact wave sources F(x,tf)=exp(tf)G(x),which can be seen very close,so that in Fig.2(b)we plot the numerical error.Upon comparing with the maximum value of wave source with 550,the maximum error 3 is very accurate.

Figure 2:For the space-time-dependent wave source recovery problem of example 2,(a)comparing recovered and exact wave sources,(b)numerical error.

4.3 Example 3

Then,we test a pointwise wave source with

Under zero initial values and boundary conditions we solve a direct problem to obtain g(x)as shown in Fig.3(a).

In this case we take ℓ=1,tf=1,nc=693,n=36.Under the convergence criterion ε=10−10the CGM is convergence with 136 steps.We take σ =0.01.In Fig.3(b)we compare the numerically recovered and exact wave sources F(x,tf)=exp(tf)δ(x−0.5),which can be seen very close,with the maximum error being 9.97×10−3.The solution of u(x,t)is plotted in Fig.3(c).

5 Numerical method to recover H(t)

In this section we recover H(t)in F(x,t)=G(x)H(t),where G(x)/=0.All the required boundary conditions,initial condition and a supplementary condition are the same as that used previously,which can be derived from exact solution.

We take x1as a reference position,and other positions are given by xi+1=x1+i(x0−x1)/m2,where x1＜x0≤ℓ.Let

be a vertical line inside Ω for each i=1,...,m2+1.At these m2+1 vertical lines,Eq.(10)is satisfied:

Multiplying Eq.(32)by G(xi+1)and Eq.(33)by G(x1)we have

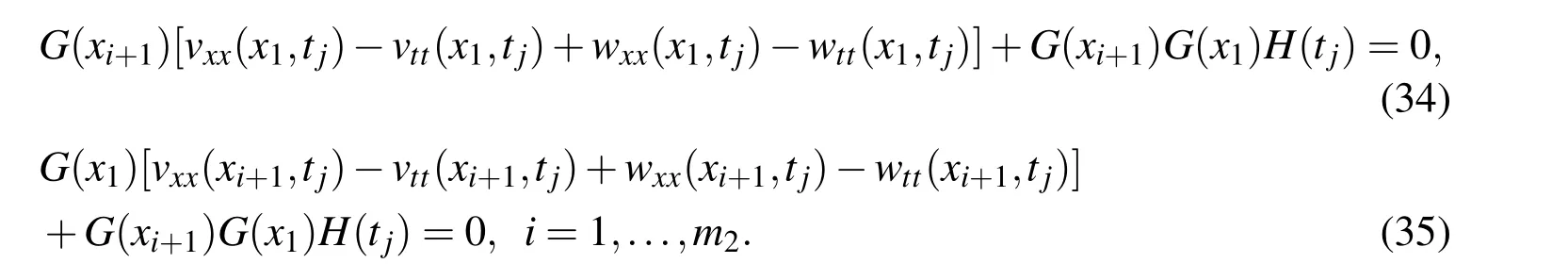
Subtracting Eq.(35)by Eq.(34),we can obtain

Figure 3:For a point time-dependent wave sourc recovery problem of example 3,(a)final time data,(b)comparing recovered and exact wave sources,and(c)recovered solution.

Then,by moving the terms about w into the right-hand side of Eq.(36),we have

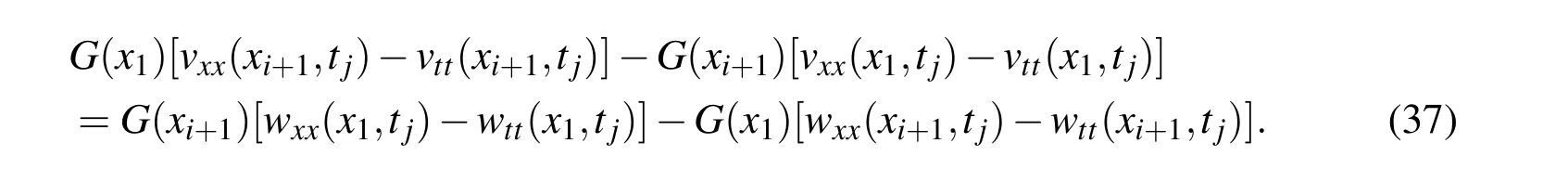
Now we can apply the CGM to solve the above linear system with dimensions m1m2×n of the coefficient matrix A to determine the n coefficients cijin Eqs.(12)and(13).

Figure 4:For the time-dependent wave source recovery problem of example 4,(a)comparing recovered and exact wave sources,(b)numerical error.

5.1 Example 4

We consider a complex inverse wave source problem with a bell shape function of t:

is a time-dependent source we attempt to recover.

In this case we take ℓ=1,tf=1,nc=700,and n=9.Under the convergence criterion ε=10−10the CGM is convergence with 15 steps.In Fig.4(a)we compare the numerically recovered and exact wave sources H(t),which can be seen very close,so that in Fig.4(b)we plot the numerical error.Upon comparing with the value of wave source with 200,the maximum error 0.93 is very accurate,although under a large noise with σ=0.5.

5.2 Example 5

We consider a complex inverse wave source problem with a sin function of t:

In this case we take ℓ=1,tf=2,σ =0.5,nc=600,and n=9.Under the convergence criterion ε=10−10the CGM is convergence with 15 steps.In Fig.5(a)we compare the numerically recovered and exact wave sources H(t),which are very close,and in Fig.5(b)we plot the numerical error.Upon comparing with the maximum value of wave source with π2,the maximum error 0.13 is small.

6 Conclusions

In this paper we have proposed a very simple homogenized function technique by including the initial condition/boundary conditions and a supplementary condition,to simplify the governing equation for the recovery of a space-dependent or a timedependent wave source,such that we can use the eigenfunctions to expand the trial solutions.Because all conditions are satisfied automatically we can collocate only a few points in the problem domain to satisfy the derived differencing equations system,whose dimension is much smaller than the collocation method in the whole problem domain.Although the supplementary data were polluted by a large noise 50%,the presented method is quite simple,very stable and very accurate to recover the space-dependent or time-dependent wave source.

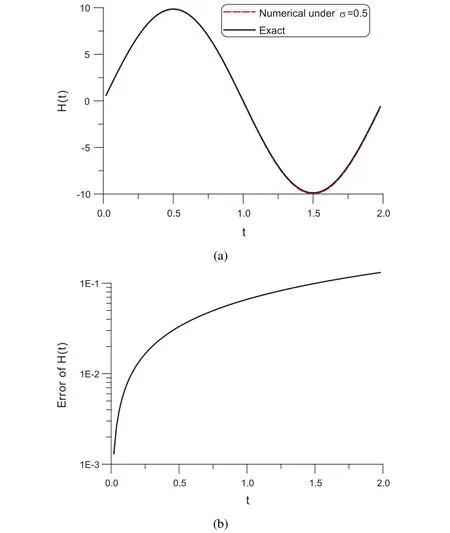
Figure 5:For the time-dependent wave source recovery problem of example 5,(a)comparing recovered and exact wave sources,(b)numerical error.

Acknowledgement:Taiwan’s Ministry of Science and Technology project NSC-102-2221-E-002-125-MY3 granted to the first author is highly appreciated.CS has been nominated to be a Chair Professor of Hohai University.

Dong,L.;Alotaibi,A.;Mohiuddine,S.A.;Atluri,S.N.(2014):Computational methods in engineering:a variety of primal&mixed methods,with global&local interpolations,for well-posed or ill-Posed BCs.CMES:Computer Modeling in Engineering&Sciences,vol.99,pp.1–85.

El Badia,A.;Ha-Duong,T.(2001):Determination of point wave sources by boundary measurements.Inv.Prob.,vol.17,pp.1127–1139.

Godinho,L.;Tadeu,A.;Amado Mendes,P.(2007):Wave propagation around thin structures using the MFS.CMC:Computers,Materials&Continua,vol.5,pp.117–128.

Gu,M.H.;Young,D.L.;Fan,C.M.(2009):The method of fundamental solutions for one-dimensional wave equations.CMC:Computers,Materials&Continua,vol.11,pp.185–208.

Jang,T.S.;Choi,H.S.;Kinoshita,T.(2000):Solution of an unstable inverse problem:wave source evaluation from observation of velocity distribution.J.Mar.Sci.Tech.,vol.5,pp.181–188.

Komornik,V.;Yamamoto,M.(2002):Upper and lower estimates in determining point sources in a wave equation.Inv.Prob.,vol.18,pp.319–329.

Komornik,V.;Yamamoto,M.(2005):Estimation of point sources and applications to inverse problems.Inv.Prob.,vol.21,2051–2070.

Kuo,L.H.;Gu,M.H.;Young,D.L.;Lin,C.Y.(2013):Domain type kernelbased meshless methods for solving wave equations.CMC:Computers,Materials&Continua,vol.33,pp.213–228.

Lin,J.;Chen,W.;Sun,L.(2015):Simulation of elastic wave propagation in layered materials by the method of fundamental solutions.Eng.Anal.Bound.Elem.,vol.57,pp.88–95.

Ma,Q.W.(2007):Numerical generation of freak waves using MLPGRand QALEFEM methods.CMES:Computer Modeling in Engineering&Sciences,vol.18,pp.223–234.

Maciag,A.(2005):Three-dimensional wave polynomials.Math.Prob.Eng.,vol.2005,pp.583–598.

Maciag,A.(2011):The usage of wave polynomials in solving direct and inverse problems for two-dimensional wave equation.Int.J.Numer.Meth.Bio.Eng.,vol.27,pp.1107–1125.

Maciag,A.;Wauer,J.(2005):Solution of the two-dimensional wave equation by using wave polynomials.J.Eng.Math.,vol.51,pp.339–350.

Ohe,T.;Inui,H.;Ohnaka,K.(2011):Real-time reconstruction of time varying point sources in a three-dimensional scalar wave equation.Inv.Prob.,vol.27,pp.115011.

Shu,C.;Wu,W.X.;Wang,C.M.(2005):Analysis of metallic waveguides by using least square-based finite difference method.CMC:Computers,Materials&Continua,vol.2,pp.189–200.

Young,D.L.;Gu,M.H.;Fan,C.M.(2009):The time-marching method of fundamental solutions for wave equations.Eng.Anal.Bound.Elem.,vol.33,pp.1411–1425.

Young,D.L.;Ruan,J.W.(2005):Method of fundamental solutions for scattering problems of electromagnetic waves.CMES:Computer Modeling in Engineering&Sciences,vol.7,pp.223–232.

1Center for Numerical Simulation Software in Engineering and Sciences,College of Mechanics and Materials,Hohai University,Nanjing,Jiangsu 210098,China

2Department of Civil Engineering,National Taiwan University,Taipei 106-17,Taiwan

3Corresponding author,E-mail:liucs@ntu.edu.tw