The Numerical Accuracy Analysis of Asymptotic Homogenization Method and Multiscale Finite Element Method for Periodic Composite Materials

Hao Dong,Yufeng Nie,2,Zihao Yang,Yang Zhangand Yatao Wu

The Numerical Accuracy Analysis of Asymptotic Homogenization Method and Multiscale Finite Element Method for Periodic Composite Materials

Hao Dong1,Yufeng Nie1,2,Zihao Yang1,Yang Zhang1and Yatao Wu1

In this paper,we discuss the numerical accuracy of asymptotic homogenization method(AHM)and multiscale finite element method(MsFEM)for periodic composite materials.Through numerical calculation of the model problems for four kinds of typical periodic composite materials,the main factors to determine the accuracy of first-order AHM and second-order AHM are found,and the physical interpretation of these factors is given.Furthermore,the way to recover multiscale solutions of first-order AHM and MsFEM is theoretically analyzed,and it is found that first-order AHM and MsFEM provide similar multiscale solutions under some assumptions.Finally,numerical experiments verify that MsFEM is essentially a first-order multiscale method for periodic composite materials.

Asymptotic homogenization method,Multiscale finite element method,First-order AHM,Slight fluctuations,Second-order AHM,Severe fluctuations.

1 Introduction

In recent years,composite materials have been widely used in engineering applications owing to their excellent physical properties compared to the traditional single component materials.However,the complexity and heterogeneity(inclusions or holes)of composite materials often cause costly computational efforts.Fortunately,mathematicians and engineers have developed some multiscale methods and other direct numerical simulation methods to solve this difficult problem in the past thirty years,such as asymptotic homogenization method(AHM),heterogeneous multiscale method(HMM),variational multiscale method(VMS),multiscale f inite element method(MsFEM)and multiscale eigenelement method(MEM),etc.We refer the interested readers to Refs.[Wu,Nie,and Yang(2014);Hou and Wu(1997);Xing and Yang(2011);Xing,Chen,and Wang(2010);Talebi,Silani,and Rabczuk(2015);Dong and Atluri(2013);Dong,Gamal,and Atluri(2013)].According to the features they possess,these multiscale methods have been divided into two categories,up-down framework and uncoupling framework[Wu,Nie,and Yang(2014)].In this paper,we focus mainly on AHM and MsFEM due to their representativeness of up-down framework and uncoupling framework respectively.To the best of our knowledge,AHM has been widely used to study thermal,electrical,magnetic and mechanical properties of composite materials[Cui(2001);Yang and Cui(2013);Han,Cui,and Yu(2009);Li and Cui(2005);Chatzigeorgiou,E-fendiev,Charalambakis,and Lagoudas(2012);Yu,Cui,and Han(2009)].AHM constructs a formal asymptotic expansion for solution of multiscale problem and provides the manner to compute zeroth-order,first-order and higher-order expansion terms.The different scales are connected by the auxiliary cell problems at the micro-scale.Considering the first-order AHM can’t provides enough micro-scale information,Cui et al.extended first-order AHM to second-order AHM and proposed a second-order two-scale method for the multiscale calculation of periodic,quasi-periodic and random composite materials[Cui(2001);Yang and Cui(2013);Han,Cui,and Yu(2009);Li and Cui(2005);Yu,Cui,and Han(2009);Yang,Cui,Nie,Wu,Yang,and Wu(2013)].In Refs.[Xing and Chen(2014c,b,a)],they study the effects of the asymptotic expansion order and the element order of finite element method used in calculation on the accuracy of AHM.However,they don’t discuss the numerical accuracy of AHM which is effected by the properties and structure of composite materials.As far as we know,there is no paper which gives a systematic analysis of the applicative scope for first-order AHM and second-order AHM.If we don’t have adequate appreciation of the applicative scope for first-order AHM and second-order AHM,we will choose an unsuitable method which causes insufficient calculation accuracy or a waste of computational resources.In addition,MsFEM is another widely used multiscale method proposed by Hou et al.The main idea of MsFEM is to construct special oscillatory finite element base functions which can capture the micro-scale information on the macroscopic mesh.In Ref.[Wu,Nie,and Yang(2014)],they give a comparative investigation of different multiscale methods from solving framework and computational cost.But still no paper investigates whether MsFEM can provide sufficient accuracy for problems which must be solved by second-order AHM.

In this paper,the numerical accuracy of AHM and MsFEM is investigated.By numerical experiments and theoretical analysis,a applicative scope of first-order AHM and second-order AHM is proposed for practical engineering calculation.Furthermore,we verify that MsFEM provides similar multiscale solutions as first-order AHM for periodic composite materials.It means that MsFEM can’t provide adequate numerical accuracy for problems which must be solved by second-order AHM.The main results of this paper are Theorem 1 in Section 2,Theorem 2 and corollary 1 in Section 3.The outline of this paper is organized as follows.In Section 2,the static heat conduction problems for four kinds of representative periodic composite materials are implemented by first-order AHM and second-order AHM.By the control variate method,the main factors to determine the accuracy of first-order AHM and second-order AHM are found and the physical interpretation of these factors is given.In Section 3,for one-dimensional static heat conduction problem,we prove that MsFEM and HMM provide similar multiscale solutions as first-order AHM under some assumptions.After that,Numerical experiments in two-dimensional case validate that MsFEM can’t provide enough accuracy for problems which must be solved by second-order AHM.In Section 4,some important conclusions for engineering application are concluded by the summary of Section 2 and Section 3.

For convenience,we use the Einstein summation convention on repeated indices in this paper.In addition,all physical quantities in this paper are dimensionless quantities.

2 The numerical accuracy analysis of first-order AHM and second-order AHM for static heat conduction problems

In this paper,static heat conduction equations are selected as the model equations to be analysed.Consider the following static heat conduction problem with homogeneous Dirichlet boundary condition:

where source term h(x)is a macro-scale function which doesn’t contain microscale information.Under the assumptions of microstructure periodicity and uniformity,AHM provides a formal multiscale asymptotic expansion solution of multiscale problem(1)as follow[Yu,Cui,and Han(2009);Cioranescu and Donato(1999)]:

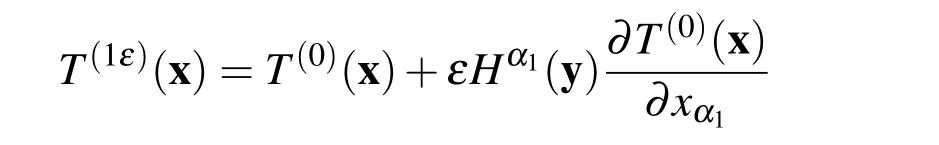
Table 1:Auxiliary cell problems and homogenized problem

as first-order AHM solutions,and

as second-order AHM solutions for static heat conduction problems(1).

For the sake of determining the applicative scope for first-order AHM and secondorder AHM,four kinds of typical periodic composite materials are used as the objects of numerical experiments.They are composite materials containing inclusions,composite materials with core-shell structure,porous composite materials and compound porous composite materials respectively.As is known to all,it is always difficult to find the analytical solutions for problem(1).Therefore,we replace Tε(x)with Te(x)which are precise FEM solutions for problem(1)in a very fine mesh.Without confusion,some notations are introduced as follows:

To the best of our knowledge,L2norm represents the accuracy of multiscale solution,H1semi-norm represents the accuracy of multiscale solution’s gradient.In practical engineering applications,engineers are more concerned about the gradient of multiscale solution because gradient represents heat flux or strain.Now,the specific numerical experiment results are given in the following subsections.

2.1 Composite materials containing inclusions

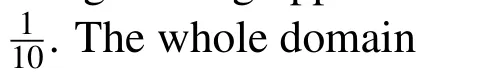
Figure 1:Geometrical configuration:(a)The whole domain Ω;(b)The unit cellY

Now,the computational cost of FEM elements and nodes forTe(x)andTε(x)is listed in Table 2.

Table 2:Mesh information

In order to analyze the influence of material coefficients on the accuracy of AHM,the control variate method is used.Firstly,the case,when the material coefficients of matrix is bigger than the material coefficients of inclusion,is denoted as case 1.Furthermore,the case,when the material coefficients of inclusion is bigger than the material coefficients of matrix,is denoted as case 2.The specific material coefficients for case 1 and case 2 are listed in Table 3.After numerical calculation,the final results are shown in Fig.2.

Table 3:Material coefficients information

Figure 2:Composite materials containing inclusions:(a)case 1;(b)case 2.

From the final results in Fig.2(b),it is easy to see that there is a big difference between the accuracy of first-order AHM and second-order AHM in case 2.In this case,only the second-order AHM can provide enough accuracy.For case 1 in Fig.2(a),the second-order AHM can’t give a significant accuracy improvement compared to the first-order AHM.

2.2 Composite materials with core-shell structure

In this subsection,the composite materials with core-shell structure are investigate.It is another common composite materials.The whole domain Ω and the unit cellYare shown in Fig.3.Similarly,Y1,Y2andY3are used to represent matrix,shell structure and inclusion in composite structure respectively.In addition,the mesh information for numerical calculation is listed in Table 4.The material coefficients for case 1 and case 2 are listed in Table 5.The final calculation results are shown in Fig.4.

Table 4:Mesh information

From Fig.4(a)and 4(b),it is clear that the final result is similar to the result of composite materials containing inclusions in the previous subsection.For case 1 in Fig.4(a),the second-order AHM can’t give a significant accuracy improvement compared to the first-order AHM.From Fig.4(b),it is easy to see that only the second-order AHM can provide enough accuracy for case 2.

Figure 3:Geometrical configuration:(a)The whole domain Ω;(b)The unit cellY

Table 5:Material coefficients information

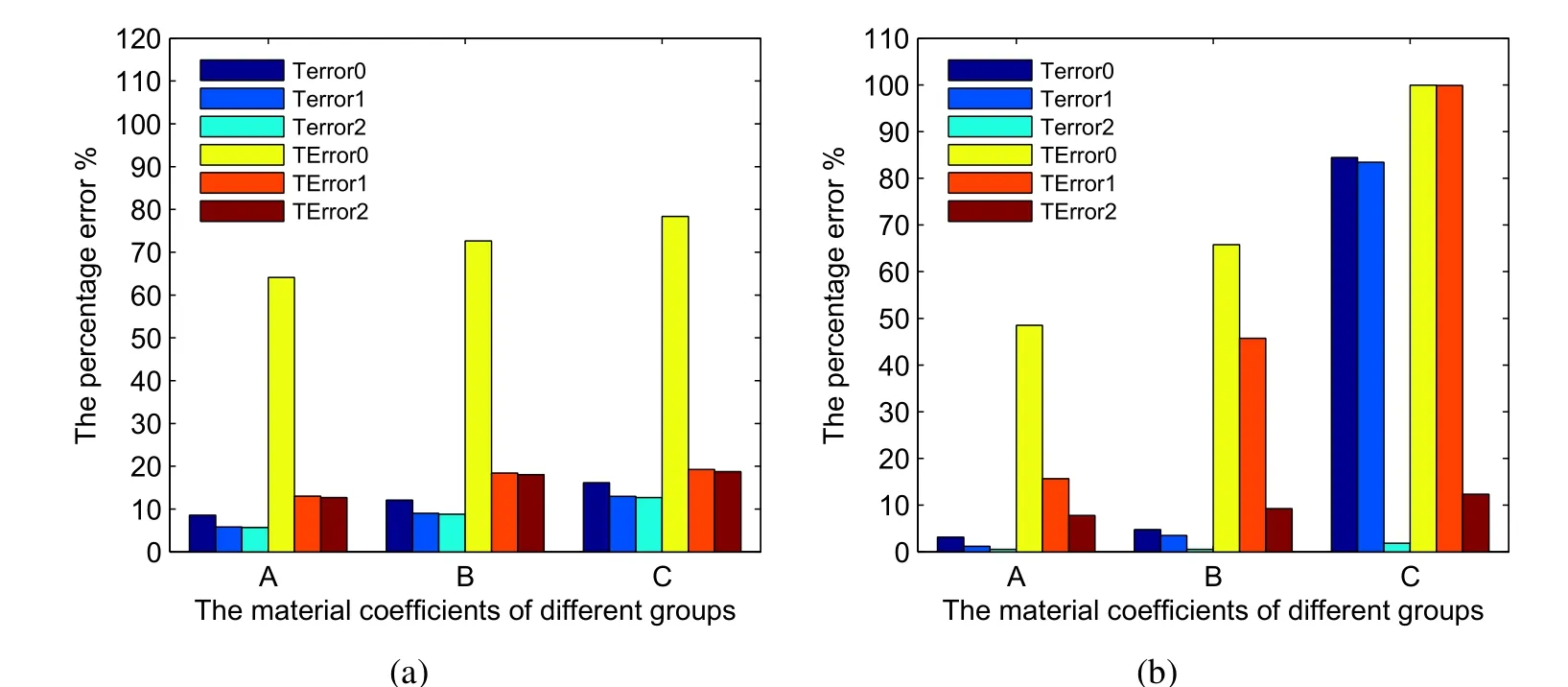
Figure 4:Composite materials with core-shell structure:(a)case 1;(b)case 2.

2.3 Porous composite materials

In this subsection,the porous composite materials are analyzed which are widely used in the fields of aviation,aerospace,machinery,etc.The whole domain Ω and theunitcellYareshowninFig.5.Besides,Y1andY2representmatrixandporousin composite structure respectively.The required mesh information for precise FEM

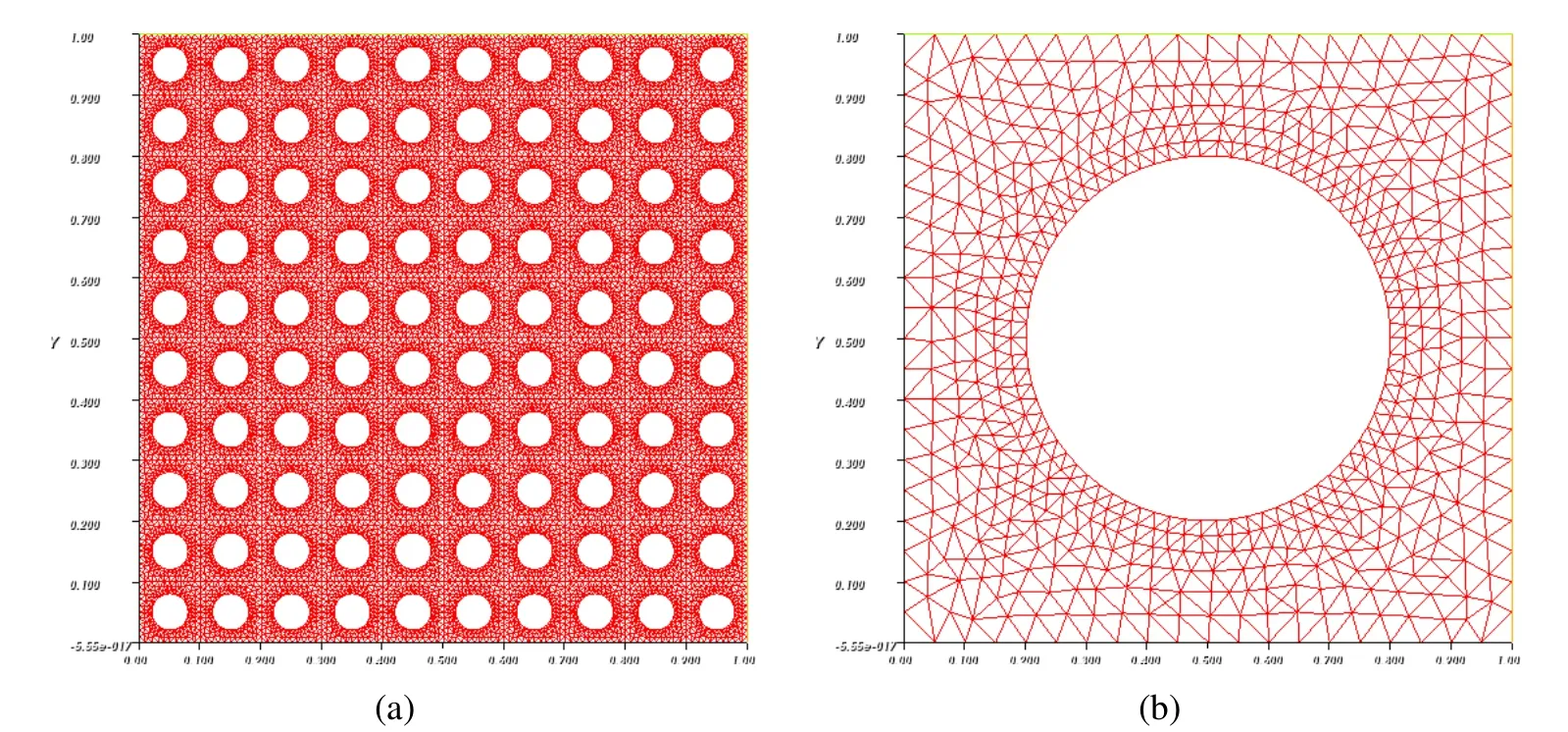
Figure 5:Geometrical configuration:(a)The whole domain Ω;(b)The unit cellY

and AHM is listed in Table 6.The detailed material coefficients are listed in Table 7.After numerical calculation,the final results are showed in Fig.6.From the relative error result in Fig.6,one can find that the accuracy of first-order AHM is enough.The second-order AHM can’t give a significant accuracy improvement compared to the first-order AHM.In addition,the accuracy of first-order AHM and second-order AHM almost not change along with the change of material coefficients.

Table 6:Mesh information

Table 7:Material coefficients information

Figure 6:Porous composite materials

2.4 Compound porous composite materials

In this subsection,the compound porous composite materials,whose whole domainΩ and unit cellYare shown in Fig.7,are considered.Then,Y1,Y2andY3are used to represent matrix,shell structure and porous in composite structure respectively.Furthermore,the required mesh information is listed in Table 8.The material coefficients for case 1 and case 2 are listed in the following Table 9.

Table 8:Mesh information

After numerical experiments,we show the final result in Fig.8.From the relative error result in Fig.8(a),one can clearly see that the first-order AHM can provide sufficient accuracy for case 1.At this time,the second-order AHM can’t give a significant accuracy improvement.For case 2 in Fig.8(b),it can be clearly seen that the first-order AHM give an unacceptable error both inL2norm sense andH1semi-norm sense.It means that only the second-order AHM can provide enough accuracy.

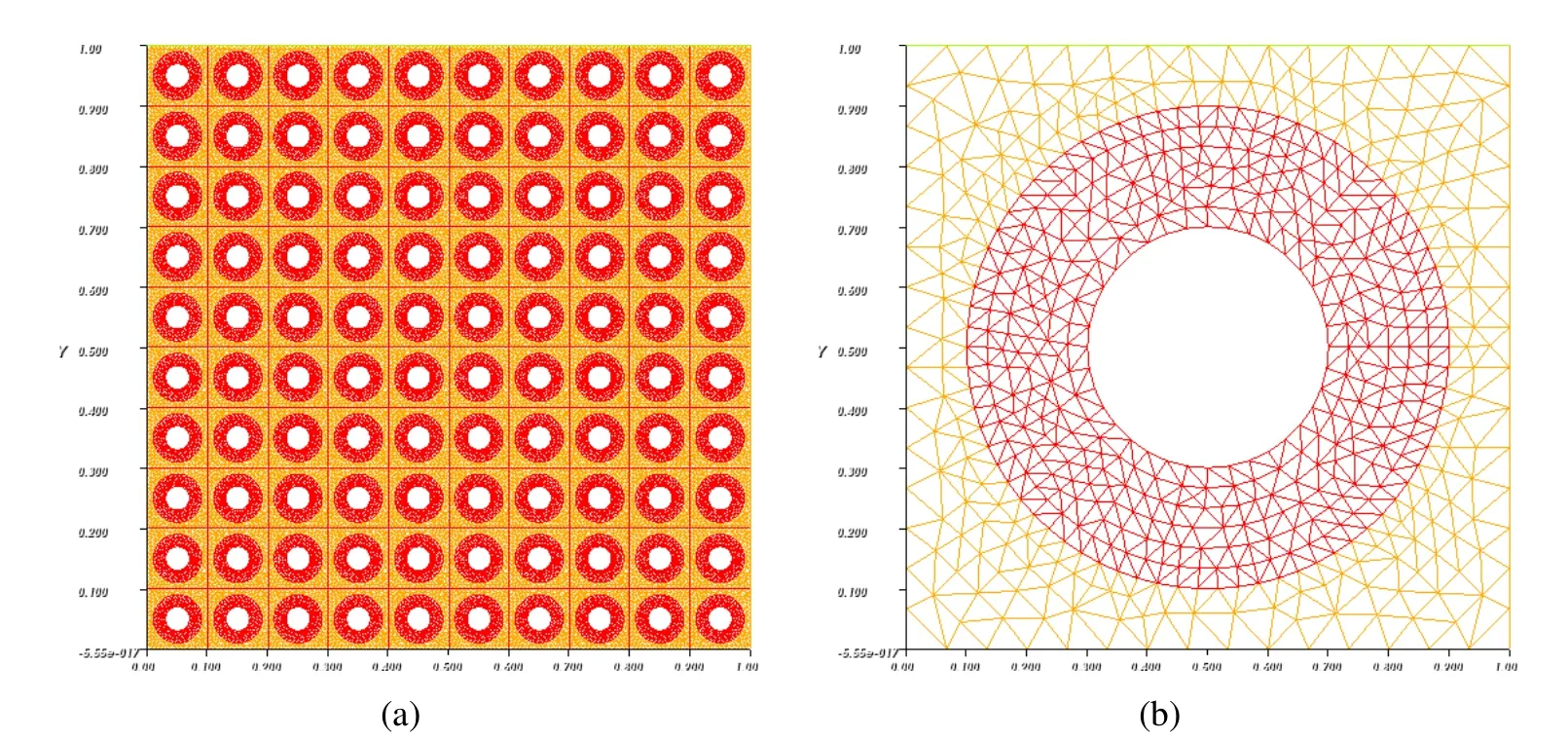
Figure 7:Geometrical configuration:(a)The whole domain Ω;(b)The unit cellY

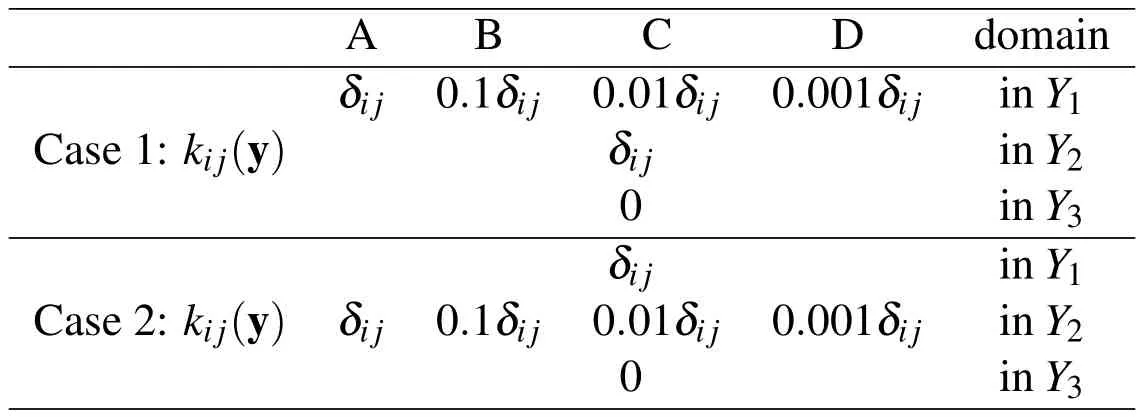
Table 9:Material coefficients information

2.5 The numerical accuracy influence by unit cell size ε

In this subsection,we study the influence of unit cell size ε on the numerical accuracy of first-order AHM and second-order AHM.Firstly,the following lemma[Cioranescu and Donato(1999)]is given:

Lemma 1For multiscale problem(1),we have the error estimate of first-order AHM solutions and second-order AHM solutions as follows:

Figure 8:Compound porous composite materials:(a)case 1;(b)case 2.

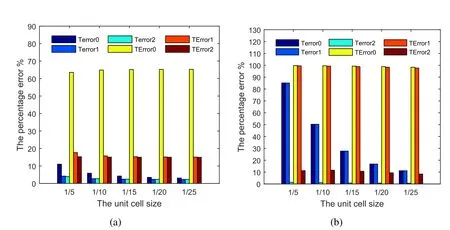
Figure 9:The different unit cell size ε from

From the final numerical result in Fig.9,one can still find that first-order AHM can provide sufficient accuracy for case 1.(D)and only the second-order AHM can provide enough accuracy for case 2.(D)along with the change of unit cell size ε.In summary,the applicative scope of first-order AHM and second-order AHM is same as subsection 2.1 even the unit cell size ε is changed.

2.6 The physical interpretation and theoretical analysis

In this subsection,the physical interpretation of the numerical results in above subsections is given.Before giving a physical interpretation,some numerical results of subsection 2.1 are shown in Fig.10 and Fig.11.From Fig.10 and Fig.11,

Figure 10:Case 1.(D):(a)Te;(b)T(0);(c)T(1ε);(d)T(2ε)

one can clearly see that multiscale solution Teshow the slight fluctuations for case 1.(D)and the severe fluctuations for case 2.(D)due to the heterogeneities of composite materials.For case 1,the heat dissipation of inclusion is bigger than matrix when matrix and inclusion absorb the same heat quantity from the heat source,because the thermal conductivity coefficient of inclusion is bigger than matrix.This cause multiscale solution Tein the inclusion region is concave compared with the surrounding matrix region.On the contrary,for case 2,multiscale solution Tein the inclusion region with smaller thermal conductivity coefficient is convex compared with the surrounding matrix region.The reason is that the heat dissipation of inclusion is smaller than matrix when matrix and inclusion absorb the same heat quantity.So we can conclude that the first-order AHM can capture the slight fluc-tuations of micro-scale and the second-order AHM is used to capture the severe fluctuations of micro-scale.

Figure 11:Case 2.(D):(a)Te;(b)T(0);(c)T(1ε);(d)T(2ε)

Then,for one-dimensional static heat conduction problems,the analytical solution can be derived by using the theory of ordinary differential equation in[Zhang,Zhou,Zhu,and Wang(2006)].Now,the following ordinary differential equation is analyzed:

whereε=1 and the thermal conductivity coefficientk(y)is listed as below:

Hence,we can get the specific form of the analytical solution in the interval[0,1]as follow:

From(10),it is easy to see thatTε(x)in the inclusion region is concave compared with the surrounding matrix region due to 5＞5/kfor case 1.Instead,multiscale solutionTε(x)in the inclusion region is convex compared with the surrounding matrix region due to 5＜5/kfor case 2.On the other hand,ifk≪1 for case 2,the fluctuation of multiscale solution in micro-scale will be more serious.In conclusion,the following theorem is derived.

Theorem 1The main factors to determine the accuracy of first-order AHM and second-order AHM are the material properties of different components and thestructure of composite materials.The first-order AHM only can capture the slight fluctuations of micro-scale due to the heterogeneities of composite materials,the second-order AHM is used to capture the severe fluctuations of micro-scale due to the heterogeneities of composite materials.

3 The accuracy analysis of MsFEM

In this section,a specific analysis of the MsFEM’s numerical accuracy is given.First of all,we theoretically prove that first-order AHM and MsFEM provide an almost identical multiscale solution for periodic composite materials under some assumptions.After that,numerical experiments verify the correctness of our conclusion.

3.1 The theoretical analysis of the MsFEM’s accuracy

In this subsection,the uniform rectangular mesh is used for macroscopic mesh and microscopic mesh of MsFEM.To facilitate theoretical analysis and numerical calculation,the macroscopic mesh sizehof MsFEM is assumed to equal to the unit cell sizeεand the macroscopic solutionTh(x)of MsFEM is approximated by bilinear base functions(see[Wu,Nie,and Yang(2014);Lu and Li(2010);Efendiev and Hou(2009);Hou,Wu,and Cai(1999)]).Moreover,we assume that the source termh(x)in multi-scale problem(1)doesn’t contain micro-scale information.As is known to all,there are two common kinds of boundary conditions for multiscale oscillatory base functions of MsFEM,the linear boundary conditions and the oscillatory boundary conditions(see[Lu and Li(2010);Efendiev and Hou(2009);Hou,Wu,and Cai(1999)]).Normally,the boundary condition of the multiscale base functions will lead a greater impact on the accuracy of MsFEM.However,the linear boundary condition will be in accord with the oscillatory boundary conditions when the material coefficients on the boundary of periodic unit cell are constant(see[Lu and Li(2010);Efendiev and Hou(2009);Hou,Wu,and Cai(1999)]).Under the above assumptions,the following theorem and its proof are given as below.

Theorem 2MsFEM provides similar multiscale solutions as first-order AHM under some assumptions.It is essentially a first-order multiscale method for periodic composite materials.

Proof:In order to simplify the analysis process,we only give the analysis for one-dimensional case.Before comparing first-order AHM and MsFEM,some definitions are given firstly.The asymptotic solution of first-order AHM for onedimensional static heat conduction problem is given as follow:

whereT(0)(x)andH(y)are the homogenized solution and the first-order auxiliary cell function of multi-scale problem(1)in one-dimensional case respectively.

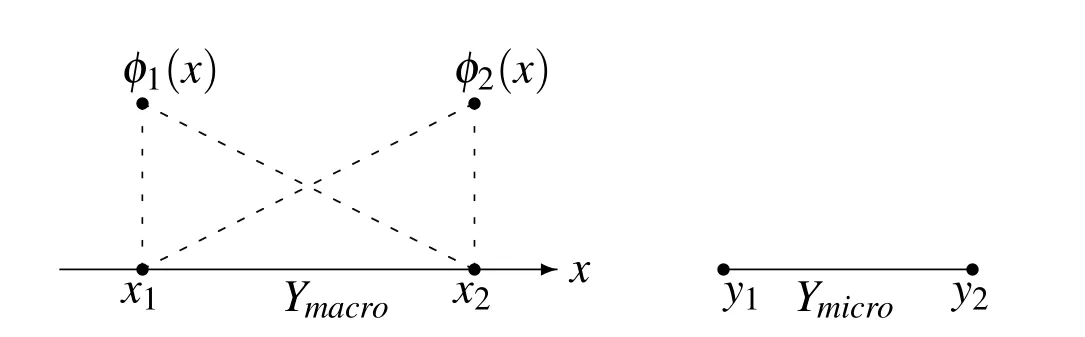
Figure 12:The unit cellYmacroin macro-scale and the unit cellYmicroin micro-scale

Furthermore,the multiscale basis functions of MsFEM for macroscopic finite elements are shown as below:

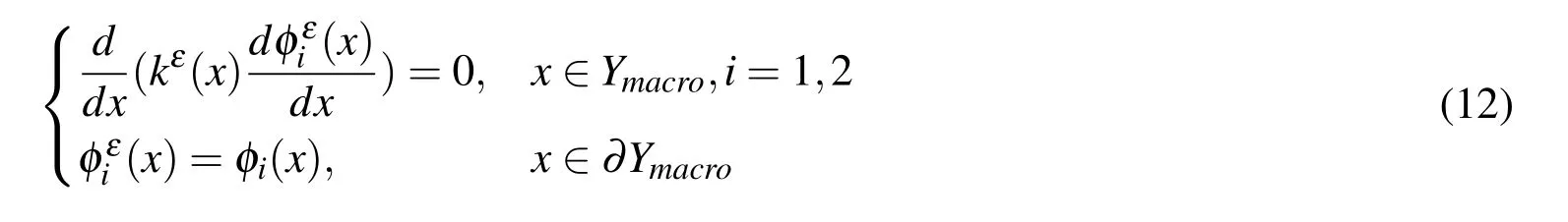
where φi(x)is the linear base function on macroscopic elements of MsFEM(Fig.12).The specific form is shown as below:

Hence,the MsFEM solution is denoted on macroscopic elementYmacroas follow:

where Th(x)is the macroscopic solution of MsFEM[Wu,Nie,and Yang(2014);Hou and Wu(1997);Efendiev and Hou(2009);Hou,Wu,and Cai(1999)].

Let Hi(x)=φεi(x)−φi(x),it is easy to obtain the following equations:

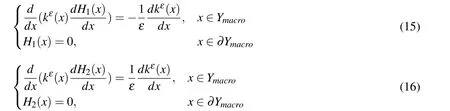
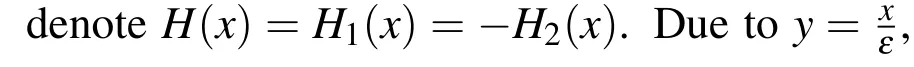
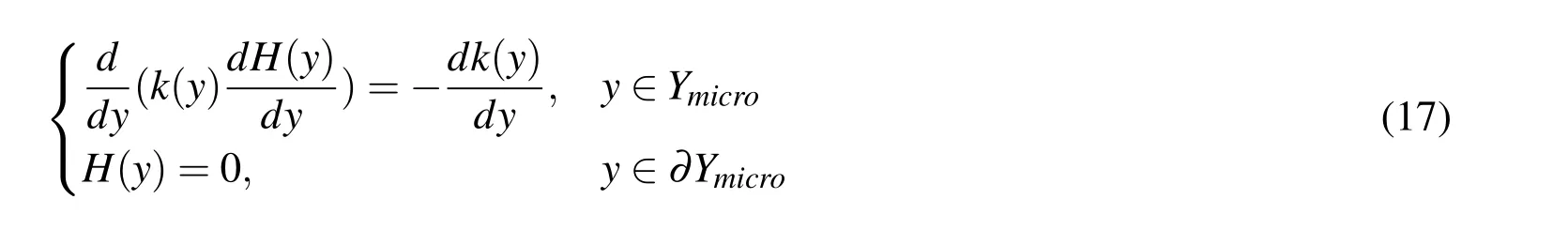
From the above derivation,we can get the following result from(13)–(17):

On the other hand,the following identity holds according to theoretical analysis in Refs.[Hou and Wu(1997);Efendiev and Hou(2009);Hou,Wu,and Cai(1999)]and numerical verification in Ref.Wu,Nie,and Yang(2014):

In conclusion,T(1ε)≈TMsFEMcan be derived under the above assumptions.Similarly,we can get the same conclusion for two-dimensional case.

Corollary 1HMM provides similar multiscale solutions as first-order AHM.It is also a first-order multiscale method for periodic composite materials.

Proof:As far as we know,the multiscale solutionsTHMM(x)for one-dimensional static heat conduction problems have the following form[Wu,Nie,andYang(2014);Efendiev and Hou(2009);E and Engquist(2003);E,Ming,and Zhang(2005)]:

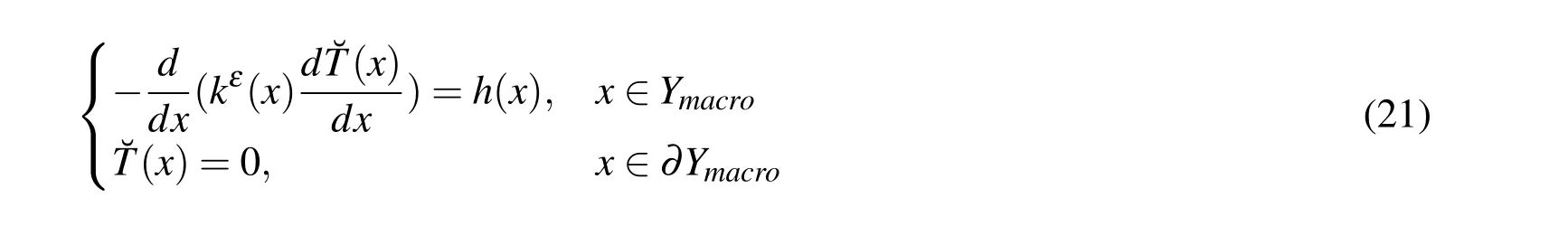
whereYmacrois a local domain of HMM and has the same size as unit cellY.

Using the same proof process as Theorem 2,the following derivation is obtained:

To our knowledge,it is not necessary to consider problem(21)when the source termh(x)of multiscale problem(1)doesn’t contain micro-scale information[Wu,Nie,and Yang(2014);Efendiev and Hou(2009);E,Ming,and Zhang(2005)].In the beginning of this section,we have assumed that the source termh(x)doesn’t have micro-scale information.Moreover,the macroscopic solutionTh(x)of HMM is almost equal to the homogenized solutionT(0)(x).Hence,we can deriveT(1ε)≈THMMunder the above assumptions.

3.2 Numerical verification

Using the control variate method as Section 2,we compare the numerical accuracy of AHM and MsFEM.The whole computational domain Ω and the unit cellYare shown in Fig.13.Let the unit cell size ε=1 in this example.In addition,the composite materials coefficients for case 1 and case 2 are listed in Table 10.

Table 10:Material coefficients information for case 1 and case 2

The undefined heat source function in problem(1)is given as follow:

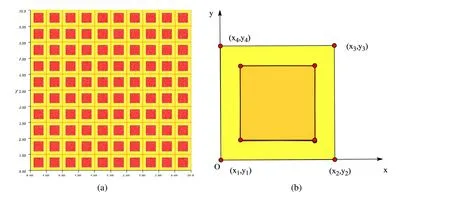
Figure 13:Geometrical configuration:(a)The whole domain Ω;(b)The unit cell Y

After that,the mesh information for AHM and MsFEM is listed in Table 11 and Table 12 respectively.

Table 11:Mesh information for AHM(triangular mesh)

Table 12:Mesh information for MsFEM(quadrilateral mesh)

In summary,from Table 13 and Table 14,one can conclude that MsFEM can capture the slight fluctuations of micro-scale due to the heterogeneities of composite materials for case 1.However,it can’t capture the severe fluctuations of micro-scale when the material coefficients of inclusion is smaller than the material coefficients of matrix.In addition,MsFEM and first-order AHM provide a nearly identical numerical accuracy for periodic composite materials(see Fig.14).

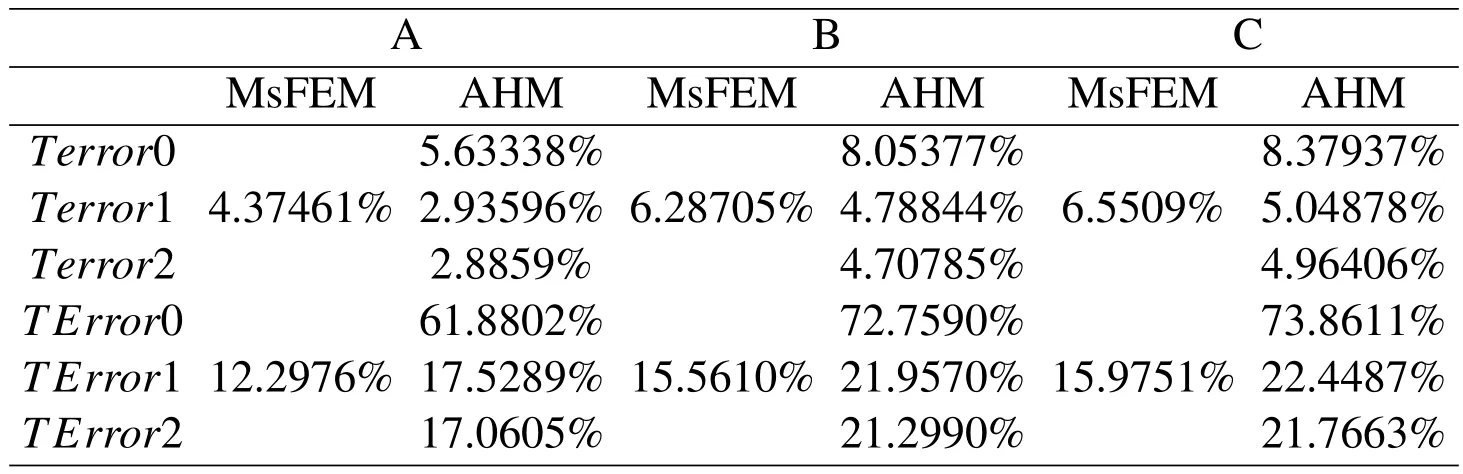
Table 13:The relative error for case 1

Table 14:The relative error for case 2

4 Conclusions

This paper mainly investigates the numerical accuracy of AHM and MsFEM for periodic composite materials.The accuracy of AHM which effects by the material properties and structure of composite materials is discussed in detail.Moreover,the numerical accuracy of MsFEM for periodic composite materials is compared with first-order AHM and second-order AHM from theoretical analysis and numerical experiments.

Now,some important conclusions for engineering application are given as follows:

(1)The first-order AHM can capture the slight fluctuations at the micro-scale due to the heterogeneities of composite materials,the second-order AHM is used to capture the severe fluctuations at the micro-scale owing to the heterogeneities of composite materials.TheL2norm error andH1seminorm error of first-order AHM and second-order AHM will all increase with the enlargement of the difference between material coefficients.

(2)The first-order AHM can provide sufficient accuracy when the material coefficients of inclusion is bigger than the material coefficients of matrix.At this time,the second-order AHM can’t give a significant accuracy improvement compared to the first-order AHM.The reason is that the solution itself does not show severe fluctuations in this case.In addition,only the second-order AHM can provide sufficient accuracy when the material coefficients of inclusion is smaller than the material coefficients of matrix because the solution itself show severe fluctuations in this case.

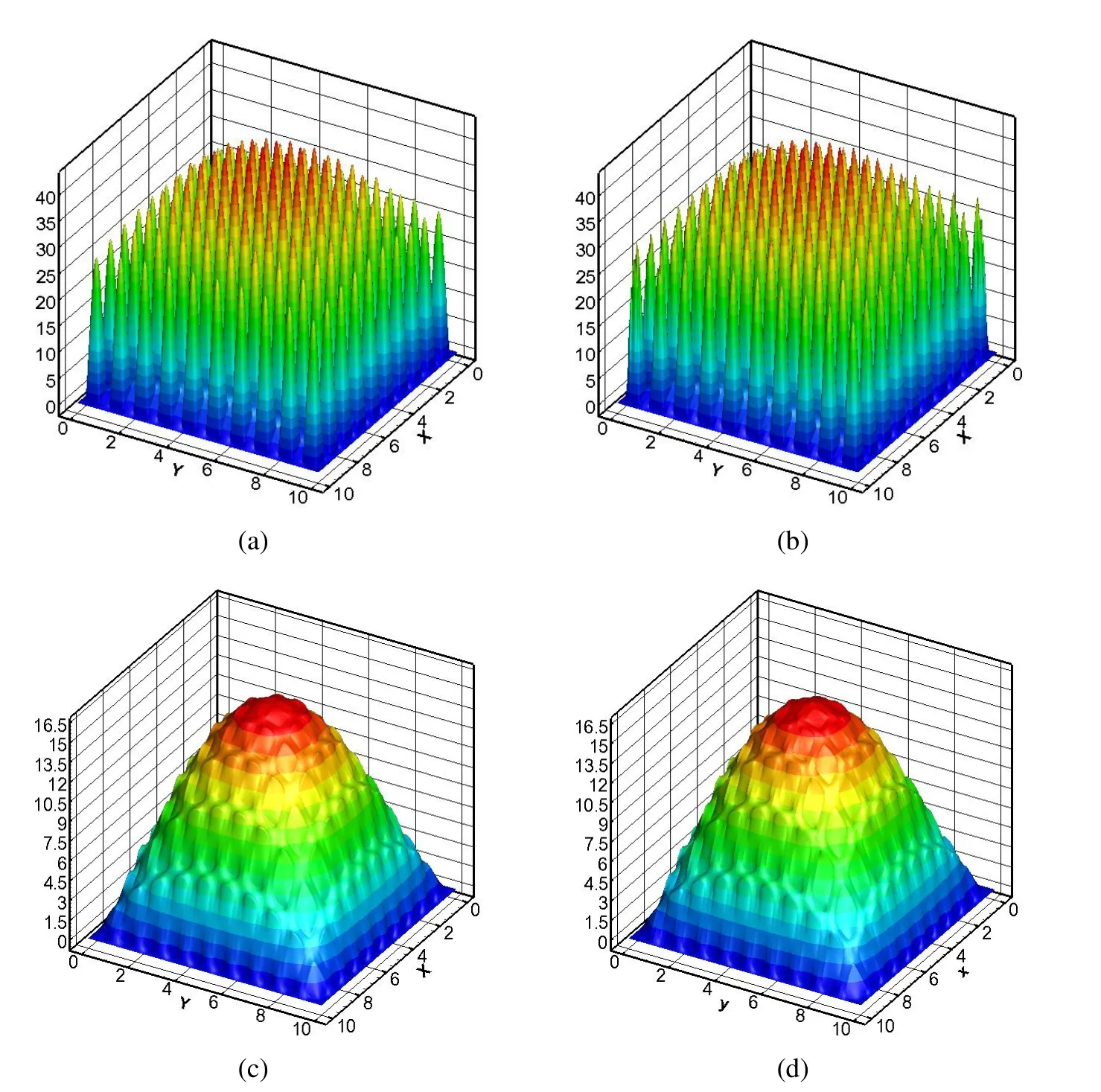
Figure 14:Case 2.(C):(a)Te;(b)T(2ε);(c)T(1ε);(d)MsFEM

(3)For the porous composite materials,the micro-scale fluctuations are very slight.In this case,the second-order AHM can’t give a significant accuracy improvement compared to the first-order AHM.Furthermore,the accuracy of first-order AHM and second-order AHM doesn’t change along with the change of material coefficients.

(4)Through theoretical analysis and numerical experiments,it is found that Ms-FEM is essentially a first-order multiscale method for periodic composite materials.It can’t capture the severe fluctuations of micro-scale when the material coefficients of inclusion is smaller than the material coefficients of matrix.But in this case,the second-order AHM can provide enough accuracy for solving this multiscale problems not only in theL2norm,but also in theH1semi-norm.Besides,we prove that HMM also is a first-order multiscale method for periodic composite materials in theoretical significance.

Acknowledgement:This work is supported by the National Natural Science Foundation of China(No.11501449 and 11471262),and also supported by the Center for high performance computing of Northwestern Polytechnical University.

Cao,L.Q.;Cui,J.Z.(2004):Asymptotic expansions and numerical algorithms of eigenvalues and eigenfunctions of the dirichlet problem for second order elliptic equations in perforated domains.Numerische Mathematik,vol.96,no.3,pp.525–581.

Chatzigeorgiou,G.;Efendiev,Y.;Charalambakis,N.;Lagoudas,D.C.(2012):Effective thermoelastic properties of composites with periodicity in cylindrical coordinates.International Journal of Solids and Structures,vol.49,no.18,pp.2590–2603.

Cioranescu,D.;Donato,P.(1999):An Introduction to Homogenization.Oxford University Press.

Cui,J.Z.(2001):Multiscale computational method for unified design of structure,components and their materials.InProceedings on Computational Mechanics in Science and Engineering,CCCM-2001,Hongkong,5-8 December,pp.33–43.Peking University Press.

Dong,L.;Atluri,S.(2013):Sgbem voronoi cells(svcs),with embedded arbitraryshaped inclusions,voids,and/or cracks,for micromechanical modeling of heterogeneous materials.CMC:Computers,Materials&Continua,vol.33,no.2,pp.111–154.

Dong,L.;Gamal,S.;Atluri,S.(2013): Stochastic macro material properties,through direct stochastic modeling of heterogeneous microstructures with randomness of constituent properties and topologies,by using trefftz computational grains(tcg).CMC:Computers,Materials&Continua,vol.37,no.1,pp.1–21.

E,W.N.;Engquist,B.(2003):The heterogeneous multiscale methods.Communications in Mathematical Sciences,vol.1,no.1,pp.87–132.

E,W.N.;Ming,P.G.;Zhang,P.W.(2005): Analysis of the heterogeneous multiscale method for elliptic homogenization problems.Journal of the American Mathematical Society,vol.18,no.1,pp.121–156.

Efendiev,Y.;Hou,T.Y.(2009):Multiscale Finite Element Methods Theory and Applications.Springer.

Han,F.;Cui,J.Z.;Yu,Y.(2009):The statistical second-order two-scale method for thermomechanical properties of statistically inhomogeneous materials.Computational Materials Science,vol.46,no.3,pp.654–659.

Hou,T.Y.;Wu,X.H.(1997): A multiscale finite element method for elliptic problems in composite materials and porous media.Journal of Computational Physics,vol.134,no.1,pp.169–189.

Hou,T.Y.;Wu,X.H.;Cai,Z.Q.(1999): Convergence of a multiscale finite element method for elliptic problems with rapidly oscillating coefficients.Mathematics of Computation,vol.68,no.227,pp.913–943.

Li,Y.Y.;Cui,J.Z.(2005): The multi-scale computational method for the mechanics parameters of the materials with random distribution of multi-scale grains.Composites Science and Technology,vol.65,no.9,pp.1447–1458.

Lu,Z.C.;Li,L.X.(2010): Application of Multiscale Finite Element Method to Heat Transfer Problems in Composite Materials.InCCCM2010 and SCCM8,Mianyang,20-25 August,pp.33–43.Peking University Press.

Talebi,H.;Silani,M.;Rabczuk,T.(2015): Concurrent multiscale modeling of three dimensional crack and dislocation propagation.Advances in Engineering Software,vol.80,pp.82–92.

Wu,Y.T.;Nie,Y.F.;Yang,Z.H.(2014):Comparison of four multiscale methods for elliptic problems.Cmes-Computer Modeling in Engineering&Sciences,vol.99,no.4,pp.297–325.

Xing,Y.F.;Chen,L.(2014):Accuracy Analysis of Mathematical Homogenization Method for Several Periodic Composites.Acta Aeronautica et Astronautica Sinica,vol.36,no.5,pp.1–9.

Xing,Y.F.;Chen,L.(2014): Accuracy of multiscale asymptotic expansion method.Composite Structures,vol.112,pp.38–43.

Xing,Y.F.;Chen,L.(2014): Physical interpretation of multiscale asymptotic expansion method.Composite Structures,vol.116,pp.694–702.

Xing,Y.F.;Chen,L.;Wang,X.M.(2010):A multiscale eigenelement method and its application to periodical composite structures.Composite Structures,vol.92,no.9,pp.2265–2275.

Xing,Y.F.;Yang,Y.(2011):An eigenelement method of periodical composite structures.Composite Structures,vol.93,no.2,pp.502–512.

Yang,Z.H.;Cui,J.Z.(2013):The statistical second-order two-scale analysis for dynamic thermo-mechanical performances of the composite structure with consistent random distribution of particles.Computational Materials Science,vol.69,pp.359–373.

Yang,Z.H.;Cui,J.Z.;Nie,Y.F.;Wu,Y.T.;Yang,B.;Wu,B.(2013):Microstructural modeling and second-order two-scale computation for mechanical properties of 3d 4-directional braided composites.Cmc-Computers Materials&Continua,vol.38,no.3,pp.175–194.

Yu,Y.;Cui,J.Z.;Han,F.(2009):The statistical second-order two-scale analysis method for heat conduction performances of the composite structure with inconsistent random distribution.Computational Materials Science,vol.46,no.1,pp.151–161.

Zhang,G.X.;Zhou,Z.M.;Zhu,S.M.;Wang,S.S.(2006):The ordinary differential equation.Higher Education Press.

1Department of Applied Mathematics,School of Science,Northwestern Polytechnical University,Xi’an 710129,PR China.E-mail:yfnie@nwpu.edu.cn

2Research Center for Computational Science,Northwestern Polytechnical University,Xi’an 710129,PR China.