三边形桅杆风荷载谱模型试验研究

孙远,占冠元

(同济大学 土木工程学院，上海 200092)



三边形桅杆风荷载谱模型试验研究

孙远,占冠元

(同济大学 土木工程学院，上海 200092)

对三边形格构式桅杆进行了均匀流和两种紊流下的高频测力天平风洞试验，得到了顺风向、横风向和扭转向的气动力系数以及脉动风荷载谱。采用基于风速谱的数学模型对顺风向脉动风荷载谱进行拟合，验证了该经验公式在不同流场下的适用性。根据试验所得横风向和扭转向脉动风荷载功率谱曲线的特点，建立由紊流激励和旋涡脱落激励两部分组成的谱函数数学模型，最小二乘法拟合结果与风洞试验结果吻合良好。横风向脉动风荷载谱以紊流激励为主，紊流强度15%时旋涡脱落激励贡献仅占10%，扭转向脉动风荷载谱中旋涡脱落激励贡献明显增大，达到40%。

格构式桅杆;高频测力天平;风洞试验;风荷载谱;参数拟合

在风来流激励下，作用于单体结构上的风荷载可以分为顺风向、横风向和扭转向风荷载3类，目前对顺风向脉动风荷载和风振响应的研究比较成熟，而对于横风向和扭转向风荷载的研究还很不足，主要集中在对气动力谱的认识上。横风向脉动风荷载主要由横向紊流和旋涡脱落激励两部分组合而成，影响因素复杂，很难找出适用于各类结构形式的统一表达式和计算方法，扭转风荷载主要是由建筑表面风压的不对称分布造成的，形成机理更加复杂，与顺风、横风向紊流和尾流激励都有关系。

近年来,许多风工程专家采用风洞试验的手段针对各种断面形式的高层建筑结构提出了多种类型的横风向、扭转向的气动力谱表达式[1-2]，其中针对矩形截面高层建筑的研究[3-5]最多，部分研究成果还写入了规范(如日本规范[6])。和高层结构相比，对镂空的格构式塔架的研究相对较少，梁枢果等[7]基于高频底座天平测力风洞试验，建立了3种典型格构式塔架的顺风向、横风向与扭转向一阶振型广义风荷载谱解析模型；汪之松[8]对两种钢管塔进行了风洞测力试验，采用四参数公式[2]进行了风荷载谱的拟合，并讨论了各分量的相干性。研究表明,风荷载谱与结构的高度、外形、风速、紊流度等都有关系，通常试验结果都只能反映与其试验模型一致的结构的气动力特性，在实际应用中存在很大的局限性，因此，通过风洞试验来确定横风向和扭转方向的风荷载谱是目前最常采用的现实可行的方法。

桅杆结构是由细长杆身和斜拉纤绳组成的一种高柔结构，具有强非线性，对风荷载非常敏感，在风荷载作用下易产生各种复杂的风效应，除顺风向脉动风荷载外，横风向和扭转向风荷载对结构的作用同样不可忽视。基于高频测力天平风洞试验，对三边形格构式桅杆杆身的脉动风荷载谱函数进行了分析，为风振响应和等效风荷载的研究提供了依据。

1 风洞试验简介

塔架节段模型边宽沿高度不变，几何缩尺比1∶4，模型高1.35 m，弦杆直径为25 mm、横斜杆直径均为14 mm，塔身挡风系数0.277，塔架模型见图1，坐标系和风向角定义如图2所示，X、Y为结构主轴，顺风向为X′轴，横风向为Y′轴，风洞阻塞率小于3%，不需要考虑风洞堵塞修正。试验在同济大学TJ-2水平回流式边界层风洞中进行，作用在模型上的气动力采用应变型六分量高频动态测力天平测量。天平采样频率为300 Hz，采样长度为30 s。试验时模型放置在转盘上，通过转动转盘模拟不同风向角，风向角范围0°～60°，间隔5°。

图1 风洞试验模型

对于节段试验模型可以认为高度范围内紊流度不变，试验分别在均匀流场和两种紊流场中进行。采用格栅模拟均匀紊流场并通过眼镜蛇脉动风速测试仪对风场环境进行了测试，表1给出了流场的平均风速和紊流度，模拟紊流场的顺风向和横风向脉动风速谱见图3，Von-Karman谱隐含了湍流积分尺度，和试验风速谱拟合较好，其表达式为

(1)

(2)

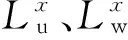
试验圆截面构件雷诺数为9.1×102～1.7×103，在亚临界范围内，格构式结构各构件尾流之间的干扰对雷诺数效应有抑制作用，且增加紊流度可以达到提高雷诺数的效果，因此,本试验中可不考虑雷诺数效应的影响。

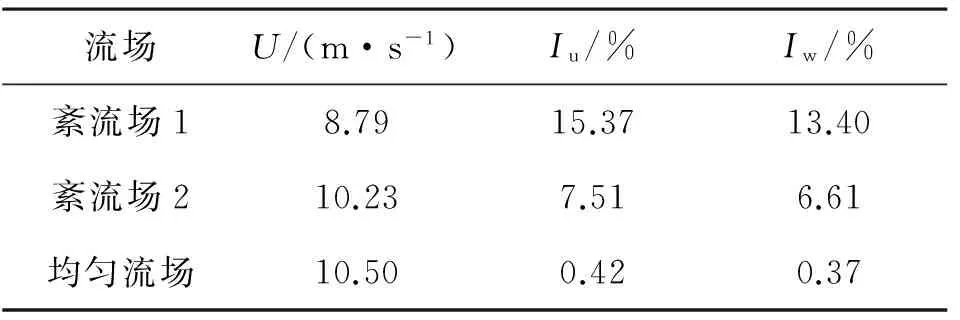
表1 主要流场特性

图3 脉动风速谱

2 试验结果与风荷载谱函数

根据顺风向阻力FD、横风向升力FL和扭矩MZ计算气动力系数

(3)

(4)

(5)

式中:ρ为空气密度；A为挡风面积，取单片桁架计算值；B为塔架边宽。

图4 不同风向角下气动力系数功率谱

2.1 顺风向脉动风荷载谱

2.1.1 顺风向脉动风荷载谱特性 作用在结构上的顺风向脉动风荷载主要由顺风向紊流引起，图5给出了不同流场下的典型风向角阻力系数功率谱，从图中可以看出，功率谱与脉动风速谱形状类似，随紊流度的增大而增大。

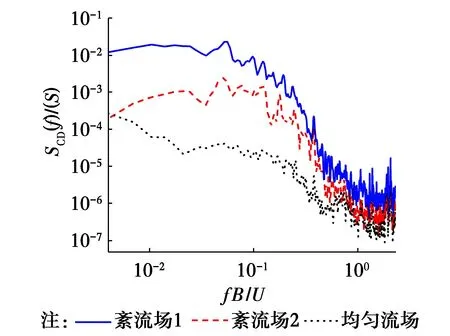
图5 不同紊流度下阻力系数功率谱

2.1.2 顺风向脉动风荷载谱密度函数 顺风向脉动风荷载主要以紊流为主，基于脉动风速谱通用表达式[10]采用经验公式进行拟合

(6)

式中：n为折减频率；A、B、C、D为待定参数，谱曲线低频斜率由参数D确定，高频斜率则受参数D-5C影响。对于顺风向脉动风荷载谱，主要关心的折减频率范围取0～1，拟合参数见表2，拟合得到的紊流场1下的顺风向脉动风荷载谱曲线同试验得到的荷载谱非常接近，见图6。采用表2的拟合参数，将紊流场2和均匀流场下的阻力系数方差代入公式(6)即可得到该风场下的阻力系数功率谱函数曲线，同试验值进行对比见图7，从图中可以看出，由经验公式得到的紊流场2的荷载谱曲线同试验值吻合良好，均匀流场的公式谱略大于试验值，总体上来看，采用拟合的经验公式计算不同紊流度风场下的荷载谱曲线可以得到比较满意的结果。

表2 顺风向脉动风荷载谱拟合参数

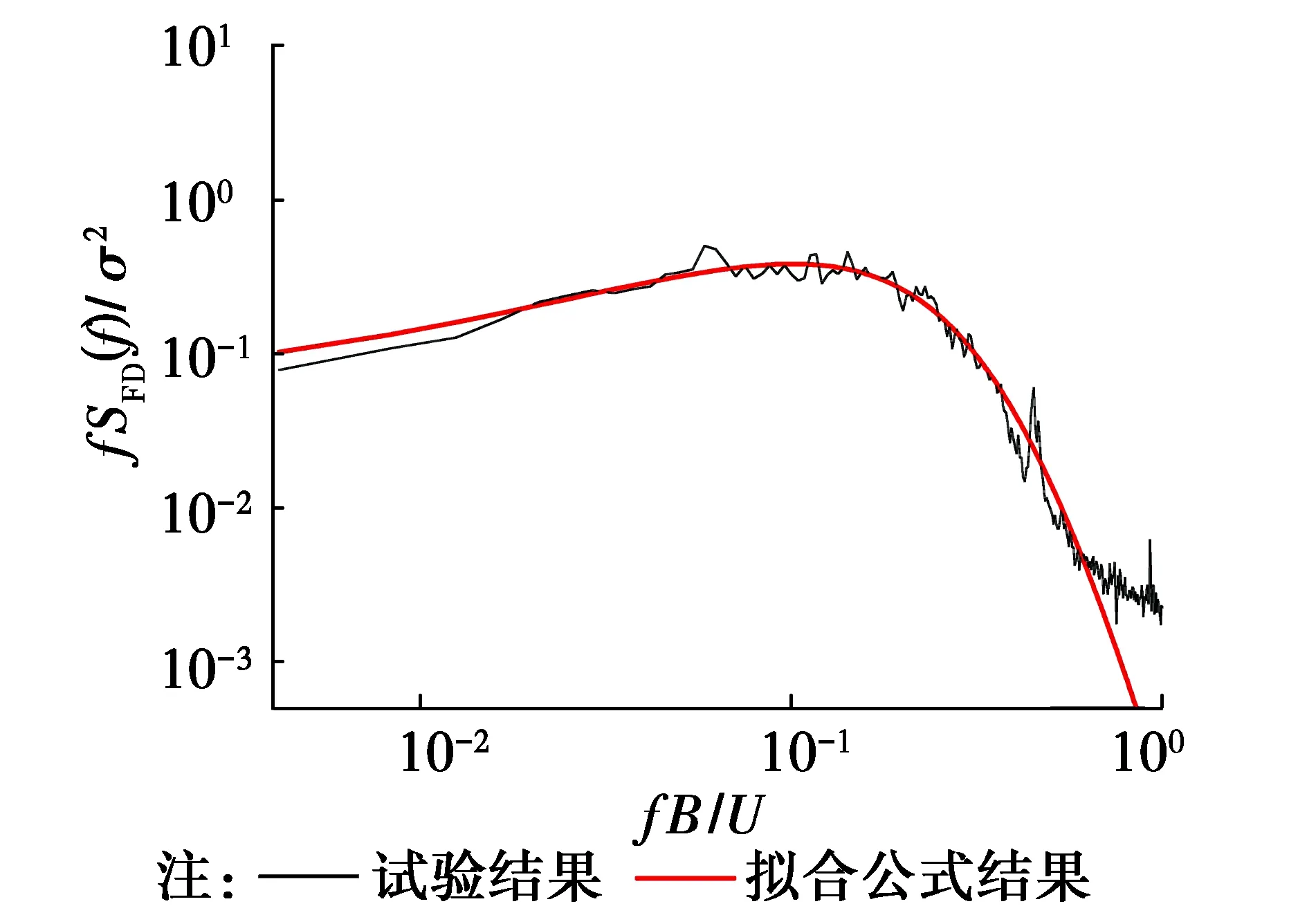
图6 紊流场1下的顺风向脉动风荷载谱

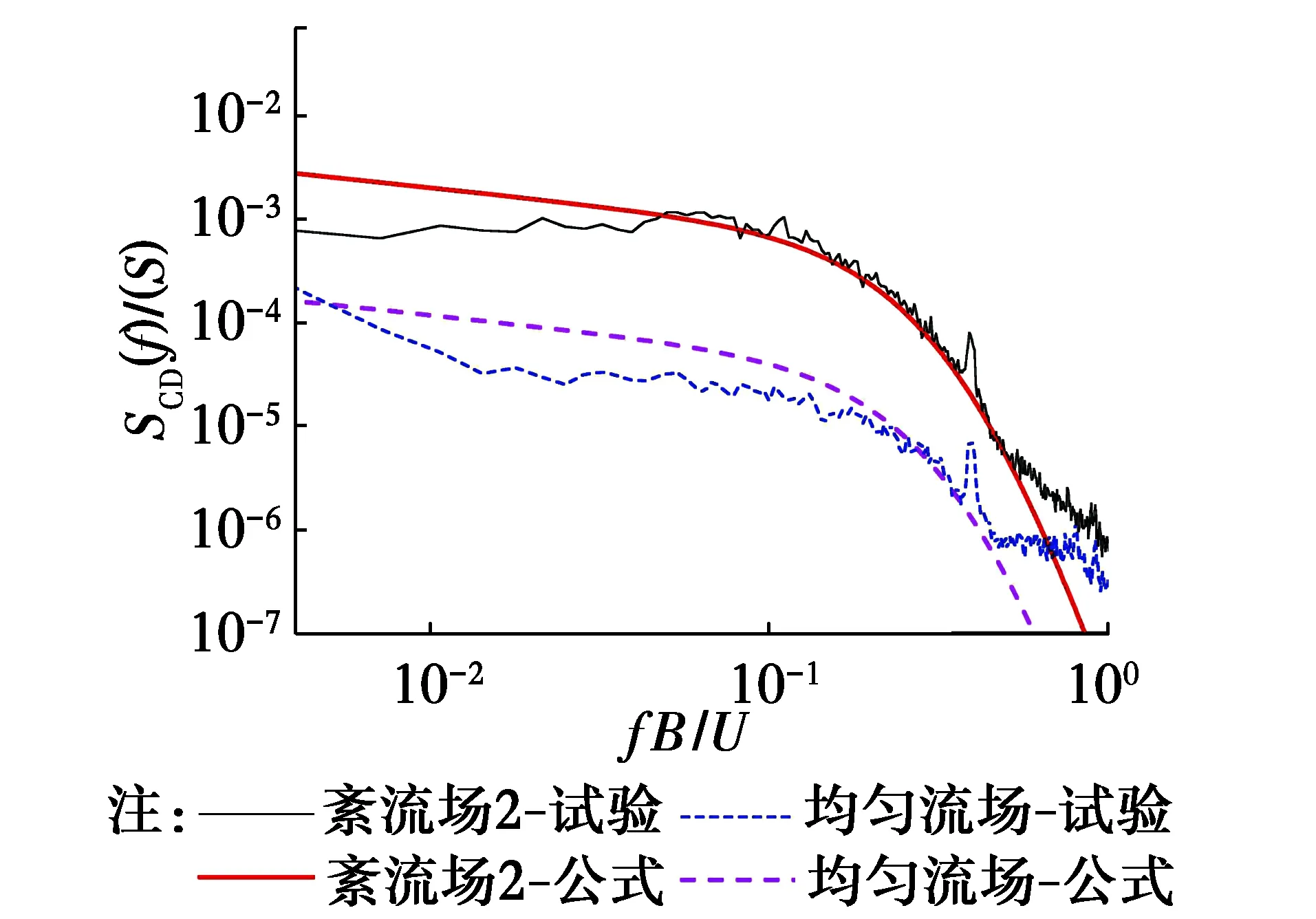
图7 紊流场2和均匀流场下的阻力系数功率谱

2.3 横风向脉动风荷载谱

2.3.1 横风向脉动风荷载谱特性 横风向脉动风荷载谱主要由紊流激励和旋涡脱落激励两部分构成[11]，不同紊流度下的典型升力系数功率谱见图8，可看出，升力系数谱有两个明显的谱峰，第一个谱峰形状同阻力系数谱相似，谱峰值折减频率在0.1左右，谱能量随紊流度的增大而增大，认为该谱峰主要由紊流激励引起，第二个谱峰受紊流强度的影响较小，不同紊流度下的谱峰折减频率基本不变，谱峰在频率轴上的位置随风速增大而右移，同风速成正比，折减频率为定值，如图9所示，符合旋涡脱落特性，说明该谱峰由旋涡脱落激励引起。

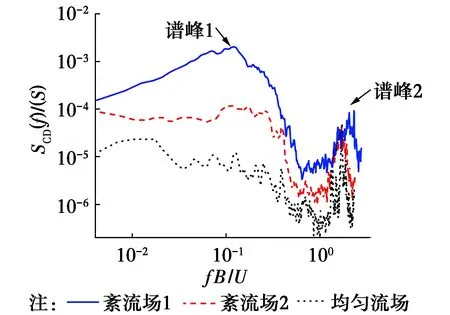
图8 不同紊流度下升力系数功率谱

图9 不同风速下升力系数功率谱

2.3.2 横风向脉动风荷载谱密度函数 采用两个分量和的形式对横风向脉动风荷载谱进行曲线拟合。

(7)

式中:第1项主要模拟紊流作用，公式同顺风向脉动风荷载谱拟合函数类似；第2项模拟旋涡脱落谱峰，该谱函数主要有高斯型和多项式型两类[12]，高斯型由细长圆柱体横向力谱得到，而多项式型一般适用于棱柱体，根据试验得到的格构式桅杆旋涡脱落谱特性，涡激力谱采用多项式表达式[13]，j为旋涡脱落谱峰数，fi为第i个涡脱谱峰的频率，fi=StU/D，其中D为结构特征尺度，Ai、αi和βi分别为谱线峰值参数、偏态参数以及带宽参数。旋涡脱落激励受构件尺寸与布置方式等多种因素影响，试验模型构件布置比较规则，各构件绕流、尾流干扰等产生的旋涡脱落频率集中在一个频段范围内，形成一个整体谱峰，故j=1。

对紊流场1下的横风向脉动风荷载谱进行最小二乘法拟合，拟合曲线见图10，从图中可以看出，拟合结果同试验结果吻合良好，格构式结构构件尺寸较小，同高层建筑相比旋涡脱落频率较大，旋涡脱落谱频带范围和紊流激励谱可以明显区分开。将经验公式中的幅值参数与横坐标参数作为变量，其他参数取值不变，对紊流场2和均匀流场下的试验谱进行拟合，得到升力系数谱结果见图11，从图中可以看出，拟合曲线可以很好的反映试验谱的特性。

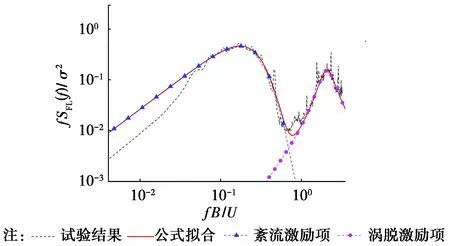
图10 紊流场1下的横风向脉动风荷载谱

不同流场的拟合参数在表3中给出，根据f1拟合值可得Strouhal数St=f1D/U，其中特征尺度取构件直径均值。假定紊流激励引起的风荷载与旋涡脱落激励引起的风荷载相互独立，则总的横风向脉动风荷载方差为

(8)

图11 紊流场2和均匀流场下的升力系数谱

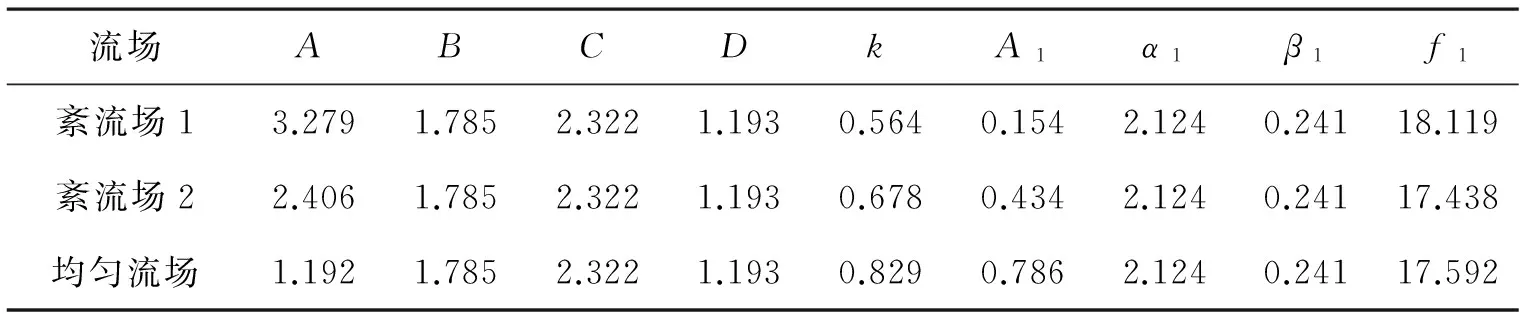
表3 横风向脉动风荷载谱拟合参数

表4 横风向脉动风荷载中两种激励百分比以及Strouhal数

以顺风向来流紊流度Iu为基本变量对谱函数峰值参数A、A1和紊流激励谱横坐标参数k进行二次拟合，得到拟合公式为

(9)

根据上式可得不同紊流度下的参数值。

2.4 扭转向脉动风荷载谱密度函数

2.4.1 扭转向脉动风荷载谱特性 从图12给出的扭矩系数功率谱中可以看出扭转向脉动风荷载谱同横风向脉动风荷载谱呈现类似的规律，由紊流激励谱和旋涡脱落谱两部分组成。

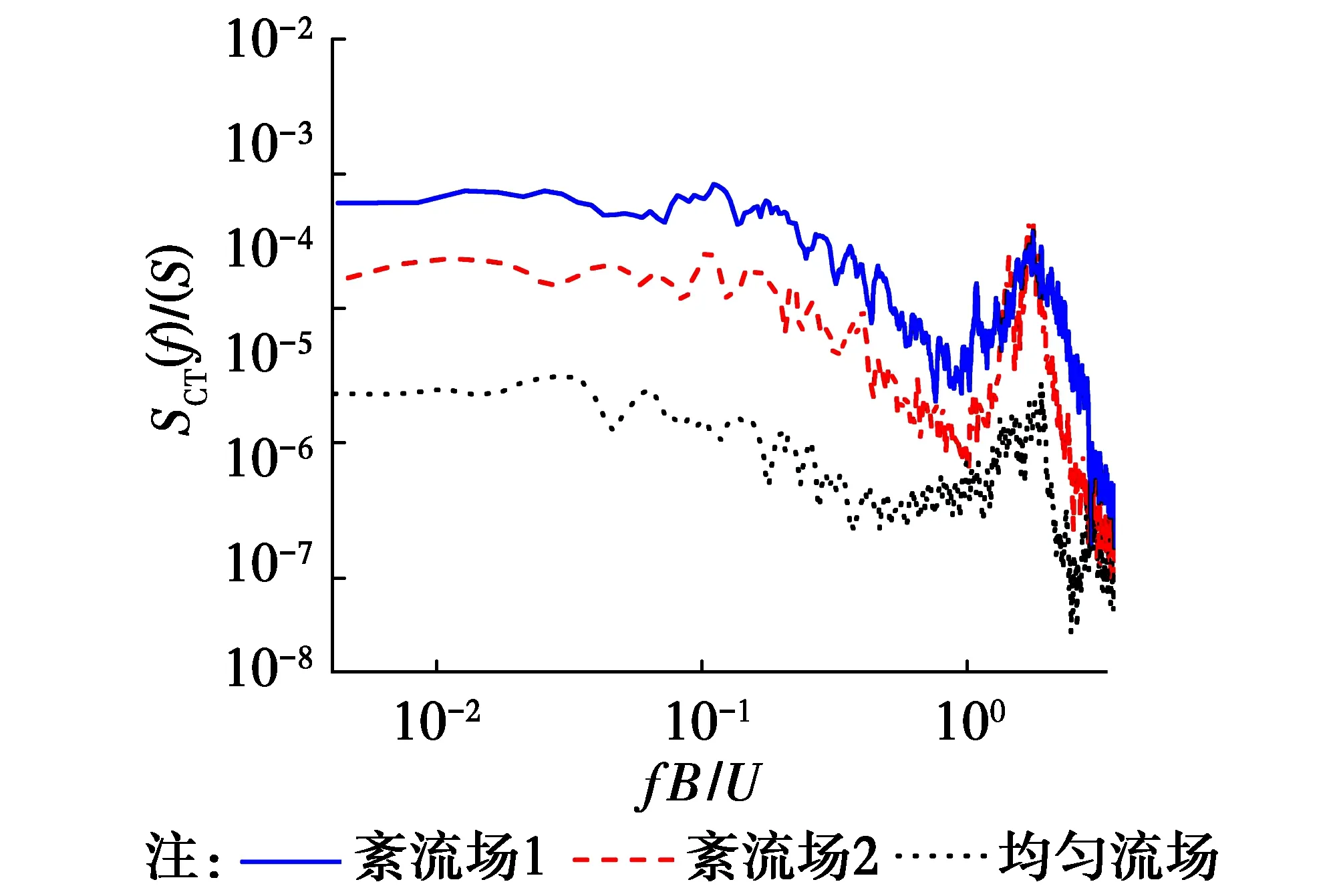
图12 不同紊流度下扭矩系数功率谱

2.4.2 扭转向脉动风荷载谱密度函数 根据扭转向脉动风荷载谱特点，采用和横风向脉动风荷载谱相同的经验公式进行拟合

(10)

式中:各参数含义同式(7)，旋涡脱落谱峰数j=1,对紊流场1下的扭转向脉动风荷载谱进行最小二乘法拟合，拟合曲线见图13，将幅值参数与横坐标参数作为变量，其他参数取值不变，对紊流场2和均匀流场下的试验谱进行拟合，得到扭矩系数谱结果见图14，从图13和14中可以看出，拟合曲线和试验结果吻合良好。

经验公式拟合参数见表5，扭转向脉动风荷载中两种激励贡献百分比以及Strouhal数见表6，旋涡脱

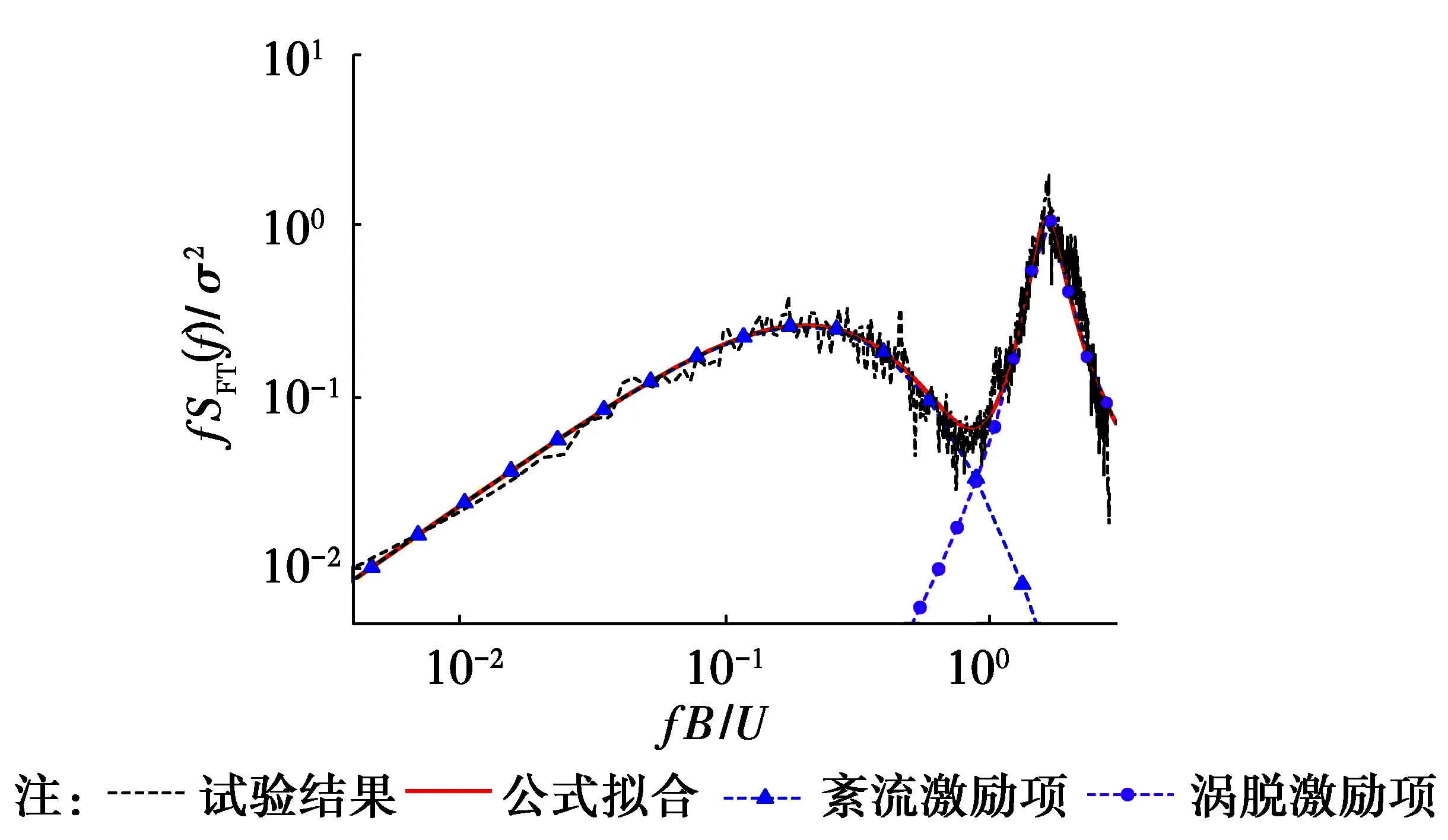
图13 紊流场1下的扭转向脉动风荷载谱

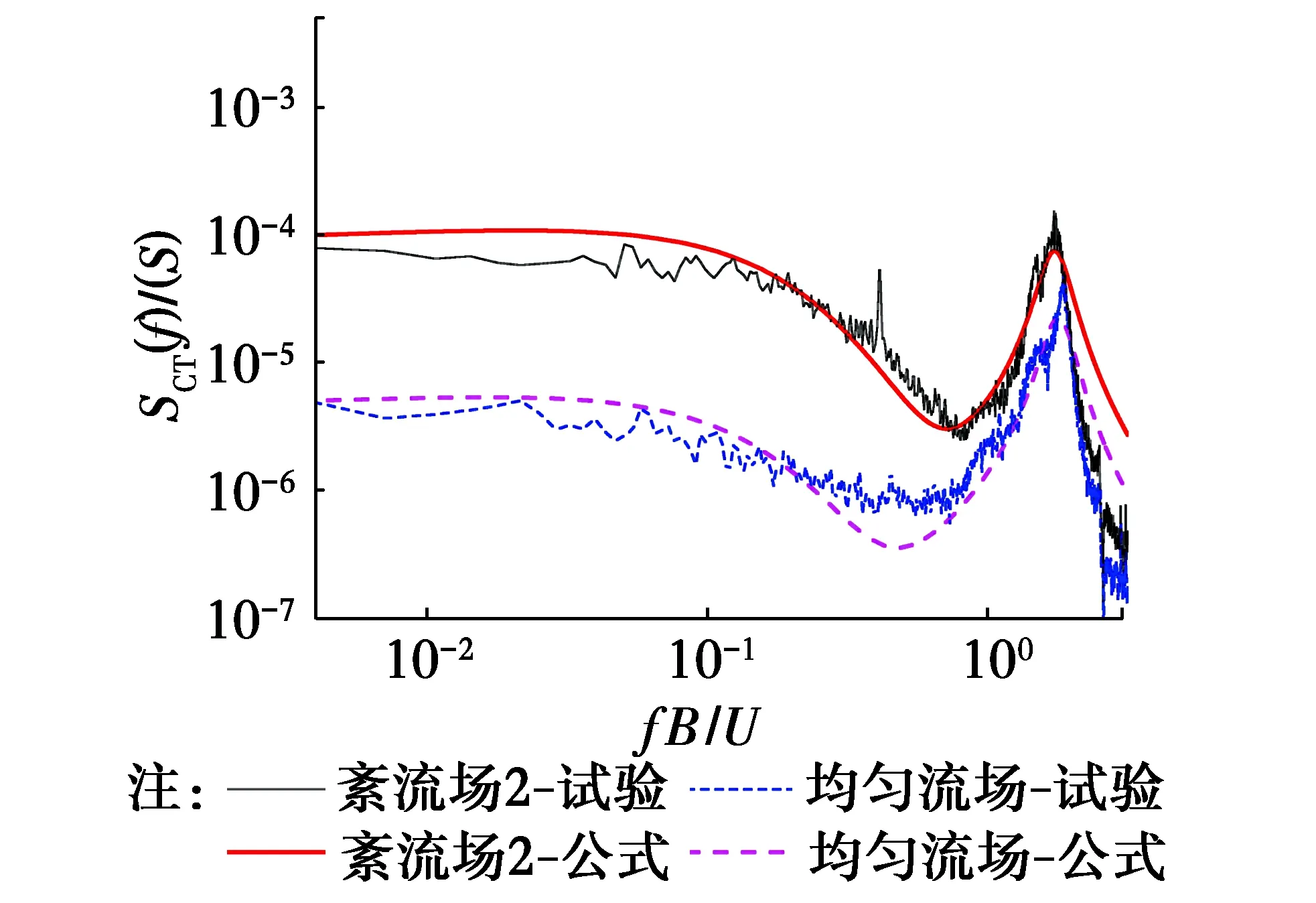
图14 紊流场2和均匀流场下的扭矩系数谱

落Strouhal数值在0.13左右，旋涡脱落激励贡献在均匀流场下为94.9%，紊流度8%时减小到70.6%，紊流度15%时为40.3%，扭转向脉动风荷载中紊流激励贡献所占比例较横风向脉动风荷载中所占比例有明显增大。

表5 扭转向脉动风荷载谱拟合参数

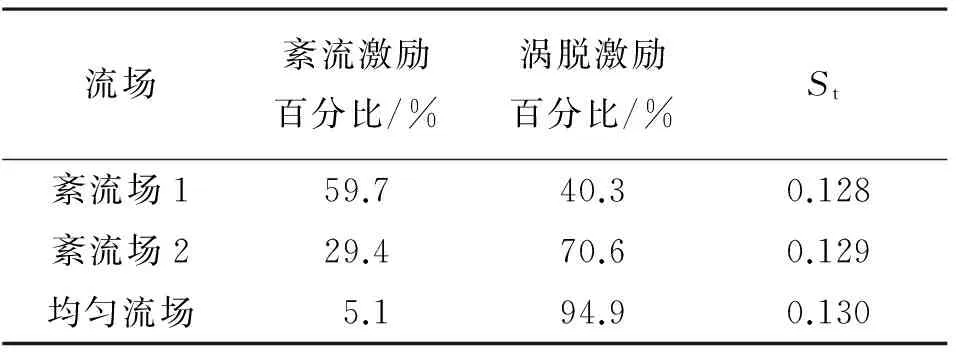
表6 扭转向脉动风荷载中两种激励百分比以及Strouhal数

以来流紊流度Iu为基本变量对谱函数峰值参数A、A1和紊流激励谱参数k进行二次拟合，拟合公式如式(11)。

(11)

根据上式可得不同紊流度下的拟合参数，从而推断出不同紊流度下的脉动风荷载谱，为风振响应分析提供依据。

3 结 论

基于高频天平测力试验，采用最小二乘法拟合三边形格构式桅杆的脉动风荷载谱，得到以下结论：

1)顺风向脉动风荷载谱同脉动风速谱相似，采用基于风速谱通用表达式的经验公式进行拟合，结果与试验曲线吻合良好。

2)横风向和扭转向脉动风荷载谱由紊流激励和旋涡脱落激励两部分组成，采用两个分量和的形式进行拟合，紊流激励主要集中在低频段，而旋涡脱落激励频率较高，有一个明显的谱峰，Strouhal数在1.3左右。

3)横风向脉动风荷载以紊流激励为主，在紊流度15%时，紊流激励贡献达到89.8%，旋涡脱落激励贡献仅占10.2%，同横风向脉动风荷载相比，旋涡脱落激励对扭转向脉动风荷载的贡献明显增大，在紊流度15%时占40.3%。

[1] GU M, QUAN Y. Across-wind loads of typical tall buildings[J].Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92: 1147-1165.

[2] 全涌. 超高层建筑横风向风荷载及响应研究[D]. 上海：同济大学， 2002.

QUAN Y. Super high-rise buildings’ wind loads and response in across-wind direction[D]. Shanghai: Tongji University， 2002.(in Chinese)

[3] LIANG S G, LIU S C, LI Q S, et al. Mathematical model of acrosswind dynamic loads on rectangular tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90: 1757-1770.

[4] LIANG S G, LI Q S, LIU S C, et al. Torsional dynamic wind load on rectangular tall buildings[J]. Engineering Structures, 2004，26: 129-137.

[5] LIN N, LETCHFORD C, TAMURA Y, et al. Characteristics of wind forces acting on tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93: 217-242.

[6] Recommendations for Loads on Buildings：AIJ 2004[S]. Tokyo: Architectural Institute of Japan, 2004.

[7] 梁枢果，邹梁浩，赵林，等. 格构式塔架动力风荷载解析模型[J]. 同济大学学报(自然科学版)，2008, 36(2): 166-171.

LIANG S G, ZOU L H, ZHAO L, et al. Analytical model of dynamic wind loads on lattice towers[J]. Journal of Tongji University(Natural Science), 2008, 36(2): 166-171.(in Chinese)

[8] 汪之松. 特高压输电塔线体系风振响应及风振疲劳性能研究[D]. 重庆: 重庆大学，2009.

WANG Z S. Study on wind-induced response and fatigue of UHV transmission tower-line coupled system[D]. Chongqing: Chongqing University, 2009.(in Chinese)

[9] 吴承卉，黄铭枫，姜雄，等. 基于半刚生模型风洞试验的锅炉塔架风振分析[J]. 空气动力学学报, 2015, 33(3): 353-359.

WU C H, HUANG M F, JIANG X, et al. Wind-induced vibration analysis of lattice-truss tower installed with a boiler based on semi-rigid model test[J]. Acta Aerodynamica Sinica, 2015, 33(3): 353-359. (in Chinese)

[10] OLESEN H R, LARSEN S E, HOJSTRUP J. Modelling velocity spectra in the lower part of the planetary boundary layer[J]. Boundary-Layer Meteorology， 1984, 29(3): 285-312

[11] 张建国，叶丰，顾明. 典型高层建筑横风向气动力谱的构成分析[J]. 北京工业大学学报，2006, 32(2): 104-109.

ZHANG J G, YE F, GU M. Amplitude characteristics of wind pressure on super high-rise buildings[J]. Journal of Tongji University of Technology， 2006, 32(2): 104-109.(in Chinese)

[12] 顾明，叶丰. 高层的横风向激励特性和计算模型的研究[J]. 土木工程学报, 2006, 39(2): 3-5.

GU M, YE F. Characteristics and computational model of across wind load of tall buildings[J]. Civil Engineering Journal, 2006, 32(2): 104-109. (in Chinese)

[13] SOLARI G. Mathmatical model to predict 3-D wind loading on buildings[J]. Journal of Engineering Mechanics, 1985, 111(2): 254-276

[14] 李秋胜，李慧真，李毅. 椭圆形高耸结构风荷载特性的试验研究[J]. 湖南大学学报(自然科学版)，2015，42(1): 1-8.

LI Q S, LI H Z, LI Y. Experimental study of the characteristics of wind loads on an oval-shaped high-rise structure[J]. Journal of Hunan University(Natural Science), 2015, 42(1): 1-8.(in Chinese)

[15] 马文勇，张晓斌，李玲芝，等. 临界雷诺数区准椭圆形覆冰导纳的风压特性研究[J]. 实验流体力学, 2014, 28(5):53-58.

MA W Y, ZHANG X B, LI L Z, et al. Study on wind pressure characteristics on quasi-oval shaped iced conductor at critical Renolds numbers regime[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(5):53-58. (in Chinese)

(编辑 胡玲)

Experimental investigation on the mathematical models of wind load spectrum for triangular lattice mast

Sun Yuan, Zhan Guanyuan

(College of Civil Engineering, Tongji University, Shanghai 200092, P.R.China)

High frequency force balance test was conducted on triangular lattice mast and the along-wind, across-wind and torsional wind load spectra and mean force coefficients were obtained. The mathematical model based on the wind velocity function was used for the curve fitting of the along-wind load spectra and the applicability of the empirical formula in different flow fields was verified. Mathematical model consisted of turbulence and wake excitation was established for the across-wind load and torsional wind load according to the characteristics of the test spectra. Fitting results of least square method showed that the mathematical models were in good agreement with the test results. The contribution of turbulence excitation was dominant in across-wind load and the proportion of wake excitation was only 10% when the turbulent intensity was 15%. In torsional wind load the contribution of wake excitation increased obviously and accounted for about 40%.

lattice mast; high frequency force balance; wind tunnel test; wind load spectrum; parameter fitting

�坐标系和风向角Fig.2

ystem and wind direction

2016-01-10

孙远(1990-)，女，博士生，主要从事高耸钢结构研究，(E-mail)2012sunyuan@tongji.edu.cn。

TU312

A

1674-4764(2016)04-0108-07

10.11835/j.issn.1674-4764.2016.04.016

Received:2016-01-10

Author brief：Sun Yuan (1990-), PhD candidate, main research interest: high-rise steel structure,(E-mail)2012sunyuan@tongji.edu.cn.