复杂地表地震勘探中的高精度近地表速度建模方法

[摘 要]在勘察内蒙阿拉善某高放废物地质处置预选场址目标花岗岩体完整性与稳定性的地震勘探过程中,利用基于MSFM(Multistencils Fast Marching Methods)射线追踪算法的地震初至波走时反演方法进行了近地表高精度速度建模研究。获得了准确、精细的近地表速度模型成果。该成果不但可被用于解决对于陆上复杂地表地震勘探来说至关重要的层析静校正问题,而且可作为地震解释工作中重要的参考资料。
[关键词]高放废物地质处置; 复杂地表; 近地表速度建模; 射线追踪; 速度反演
中图分类号:P5 文献标识码:A 文章编号:1009-914X(2016)23-0013-02
根据以往的探测经验可知,近地表速度不准确会严重影响地下地质结构的地震成像效果,对于地表条件复杂的工区更是如此。在勘察内蒙阿拉善某高放废物地质处置预选场址目标花岗岩体的过程中,为了解决对于陆上工区地震勘探至关重要的层析静校正问题,利用基于MSFM(Multistencils Fast Marching Methods, 多模板快速步进)射线追踪算法的地震初至波走时反演技术,建立了沿地震测线准确、精细的近地表速度模型。该成果不但被用于有效解决了后续的层析静校正问题,而且是最终地震地质解释工作中精确、可靠的参考资料。
1 方法原理
复杂地表问题通常指包含剧烈起伏的崎岖地表和强速度变化的近地表速度结构。在选择适用于复杂地表初至波走时反演的射线追踪算法时,通常需要考虑计算精度、计算效率、以及算法对于模型复杂度的适应能力三个方面[1]。
1.1 MSFM走时计算公式
MSFM(Multistencils Fast Marching Methods)多模板快速步进算法是由Hassouna等提出的对于经典FMM方法[2]的改进算法[3]。其原理是在标准FMM算法的基础上通过坐标旋转产生多个FMM计算模板,使对角方向邻点也能够参与计算。该算法相对标准FMM方法在计算精度方面有显著提高,并且更容易推广到处理高维高阶问题。
其计算公式如下(为了简化讨论,仅列举横向和纵向空间步长相等时的情况):
① 相邻模板(S1):
对于方向导数的一阶近似,可通过下式求解:
(1)
对于方向导数的二阶近似,可通过下式求解:
(2)
② 对角模板(S2):
对于方向导数的一阶近似,可通过下式求解:
(3)
对于方向导数的二阶近似,可通过下式求解:
(4)
在上述公式(1)~公式(4)中,为待求结果(也就是理论计算走时),为地下介质空间慢度的函数,为空间步长,为邻域范围内的最小到达时。
1.2 算法实现过程
算法的实现需要利用Dijkstra算法思想[4],即首先将计算网格点划分成三个子集,分别为到达时已确定的{已知点子集(known)},已经被计算但最终到达时待定的{窄带子集(narrow_band)}和尚未被计算的{远点子集(far)}:
(1) 首先将炮点初始化为{已知点子集},到达时为零;并根据MSFM模板计算炮点所有在{远点子集}中的邻点的到达时,并将这些点移入{窄带子集}.
(2) 选取{窄带子集}中走时最小的网格点移入{已知点子集},并利用模板计算该点所有在{窄带子集}和{远点子集}内的邻点的到达时;若邻点在{远点子集}中,则将该点移入{窄带子集};若在{窄带子集}中,则根据到达时大小选择更新或者保持原到达时(取较小者)。
(3) 重复实施步骤(2)直至所有网格点移入{已知点子集}。
1.3 Model94模型测试
为了检验MSFM射线追踪算法的计算精度及其对于复杂模型的适应能力,本次研究首先设计了针对Model94复杂地表模型的测试试验。具体试验流程为:① 给定观测系统,利用时间2阶、空间20阶交错网格有限差分法[5]求解声波方程正演出一套地震记录。② 利用2阶MSFM算法计算在相同观测系统下各检波点位置的波前面到达时(初至波到时)。③ 将MSFM计算结果投影到有限差分法地震模拟记录上,对比通过MSFM方法计算得到的初至波到达时(走时)与模拟地震录中初至波的吻合程度。
按照上述流程共进行了等间隔分布的277炮数据的数值测试试验。其中位于模型正中的第139号单炮数据数值测试结果如图1所示。
可以看到,就Model94模型复杂度的地质问题来说MSFM算法的计算精度是可以满足要求的。图中显示的波前面到时计算结果与通过高阶交错网格有限差分法得到的模拟地震记录中的初至波基本吻合。
1.4 初至波走时反演速度建模实验
相对于全波形反演(FWI)来说,射线类走时反演算法具有计算效率高、在应用中稳健可靠、人工交互技术成熟等多方面的优势。上文已经证实了即使是对于复杂地表、复杂地下结构的模型来说,MSFM射线追踪算法在计算精度方面也是能够满足要求的。因此接下来,本研究进行了后续的地震初至波走时反演速度建模实验。实验结果如图2所示。
可以看到,利用基于MSFM射线追踪算法的初至波走时反演方法进行复杂地表模型速度反演,即使是从一个与真实模型差别很大的初始模型出发(如图2a所示),经过多次迭代(图2b)最终得到的反演结果依然能够保证近地表速度分布的精确重建(图2c)。
2 复杂地表大型花岗岩体地震勘探中的应用实效
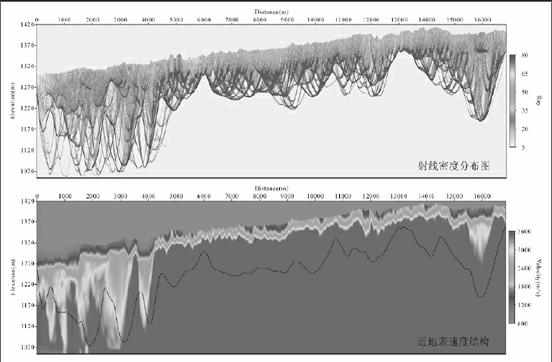
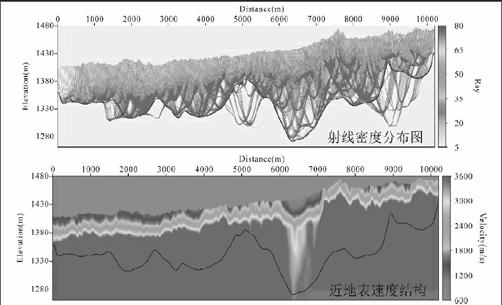
将前述基于MSFM射线追踪算法的地震初至波走时反演方法应用于内蒙阿拉善崎岖地表工区高放废物地质处置预选场址目标花岗岩体地震勘探工作中,人工拾取地震初至波(包括直达波、回转波、折射波或多个层折射波的组合)走时,进行速度反演建模,所得的建模结果如图3和图4所示。
图3和图4分别为内蒙阿拉善1线(16.856 km)和2线(10.196 km)近地表速度建模结果,其中黑色实线对应射线密度的底界(可以认为底界以上部分的速度反演结果是非常可靠的)。
首先可以看到,本次地震勘探,有效地震射线的分布是非常密集的,因此所得到的两条测线近地表速度建模结果均应是可靠的。速度建模成果首先被应用于解决了对于陆上复杂地表工区至关重要的层析静校正问题,进而又被作为地震地质解释工作中重要的参考资料。从图3与图4中均可观察到地震波速度在横向上存在局部异常。在阿拉善1线(图3)3500 m、4200 m桩号的下方以及16000 m桩号附近的两侧,阿拉善2线(图4)6000 m、7000 m桩
号的下方,均显示出了特征明显的速度梯度突变。推测这些异常、突变特征与沿测线小型断层、凹陷构造的分布有关,但限于篇幅拟另文予以详细阐述。
3 结论与讨论
经过理论分析、模型试算、以及在内蒙阿拉善工区针对大型目标花岗岩体的地震勘探工作实践,可以认为采用基于MSFM射线追踪算法的地震初至波走时反演方法解决复杂地表条件下近地表高精度速度建模问题是可靠而且有效的。
基于MSFM射线追踪算法的初至波走时反演可以作为在我国西部、南部进行地震勘探时,当遇到复杂地表近地表速度建模问题时的针对性处理技术和解决措施。
参考文献
[1] 张钋,刘洪,李幼铭,2000,射线追踪方法的发展现状[J].地球物理学进展,15(1):36-45.
[2] Sethian J A, Popovici A M, 1999, 3-D travel time computation using the fast marching method[J]. Geophysics, 64(2): 516-523.
[3] Hassouna M S, Farag A A, 2007, Multi-stencils fast marching methods: a highly accurate solution to the eikonal equation on Cartesian domains[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(9): 1563-1574.
[4] 卢回忆,刘伊克,常旭. 20013, 基于MSFM的复杂近地表模型走时计算[J]. 地球物理学报, 56(9): 3100-3108.
[5] 王秀明, 张海澜, 2004, 用于具有不规则起伏自由表面的介质中弹性波模拟的有限差分算法. 中国科学( G 辑), 34( 5) : 481-493.
作者简介:李稳,男,1983年生,工程师,博士,主要从事地震勘探数据处理方法研究和地震资料解释工作.
资金资助:核设施退役及放射性废物治理项目(科工二司[2013]727号)、中国地震局物探中心青优专项(SFGEC2014006)
中国科技博览2016年23期
