带承台倾斜单桩水平承载变形性状数值分析

樊文甫，曹卫平

(1.西安建筑科技大学 土木工程学院，西安 710055； 2.特变电工新疆新能源股份有限公司，乌鲁木齐 830011)



带承台倾斜单桩水平承载变形性状数值分析

樊文甫1, 2，曹卫平1

(1.西安建筑科技大学 土木工程学院，西安 710055； 2.特变电工新疆新能源股份有限公司，乌鲁木齐 830011)

为研究带承台倾斜单桩水平承载变形性状，通过数值模拟手段分析了水平荷载作用下桩身倾角、长径比对桩顶带承台斜桩的承载变形性状的影响，并重点分析了竖向荷载对水平受荷斜桩性状的影响。结果表明：①水平荷载作用下，负斜桩的桩顶水平位移最大，直桩居中，正斜桩最小；桩身倾角越大，斜桩桩顶水平位移与相应直桩桩顶水平位移差值越大；相同情况下，长径比对斜桩桩顶水平位移影响不明显。②水平荷载作用下，桩身倾角只影响斜桩桩身弯矩的大小，而最大桩身弯矩的位置基本不变。③竖向荷载减小了负斜桩桩顶水平位移，却增大了正斜桩桩顶位移。④负斜桩的桩身最大弯矩随着竖向荷载的增大而减小，正斜桩却与之相反。

斜桩；水平承载特性；数值分析；长径比；桩身倾角；竖向荷载

1 研究背景

斜桩由于其良好的水平承载特性，多被应用于桥梁、码头及输电线路塔架基础等工程[1-4]。斜桩倾斜方向与水平荷载作用方向一致的为正斜桩，反之为负斜桩(如图1所示)。由于实践表明斜桩在抵抗水平荷载方面具有优势，因此研究水平荷载作用下的斜桩承载力及变形性状具有重要的工程意义。

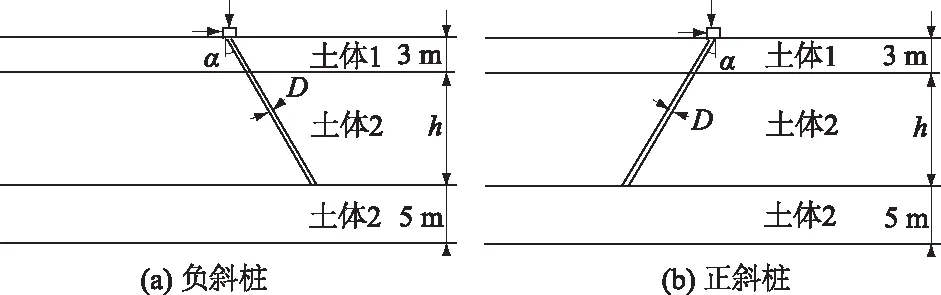
图1 模型示意图Fig.1 Sketch of batter pile model

国内外学者针对斜桩水平承载性状进行了一系列的研究。Meyerhof等[5]采用模型试验研究了在倾斜荷载作用下桩的受力变形特性，对斜桩的研究有一定的指导意义。Zhang等[6-7]通过离心机试验得到荷载-位移曲线，研究了桩身倾角和砂土密实度对斜单(群)桩水平承载力的影响。在理论研究方面，凌道盛等[8]基于浅层土体极限破坏假设，导出了浅土层中不同倾角斜桩桩侧土体极限土压力，并提出一种斜桩水平受荷的p-y曲线计算方法。实际工程中桩基仅受水平荷载作用的情况几乎不存在，常见的是竖向和水平荷载共同作用。一些学者针对竖向荷载对桩基水平承载特性的影响进行了研究。赵春风等[9]利用室内模型试验研究了砂土中直桩的承载特性，试验结果表明预先施加竖向荷载有利于直桩水平承载力的提高。袁廉华等[10]通过模型试验分析，认为轴向压力能提高斜桩的水平承载力。数值分析方面，Karthigeyan等[11]通过GEOFEM模拟分析了砂土中竖向荷载对直桩水平承载力的影响，认为在砂土中竖向荷载有利于直桩水平承载力的提高。郑刚等[12]通过ABAQUS模拟分析了直桩承载力的影响因素，得到了竖向荷载有利于减小水平荷载产生的桩侧位移的结论。

综上所述，目前多侧重于斜桩水平承载力的研究，而对桩身内力研究较少，且竖向荷载对单桩水平承载性状影响的研究大多集中于直桩，而斜桩较少。因此，本文利用有限元软件ABAQUS研究了水平荷载作用下桩身倾角、长径比对带承台斜桩承载变形的影响，并重点分析了竖向荷载对斜桩水平承载特性的影响。

2 计算模型

2.1 模型尺寸

为保证计算精度并比较真实地模拟桩-土作用，考虑到模型试验边界条件的限制，三维土柱半径取20 m，土体分为土体1和土体2(如图1所示，其中h=L·cosα-3)。桩体直径D为0.5 m，桩长L分别为15，20，30 m。为了限制桩顶自由转动以及模拟实际工程，桩顶采用与承台固结的方式，并按最小原则取承台大小为1 m×1 m×0.5 m。有限元模型见图2。

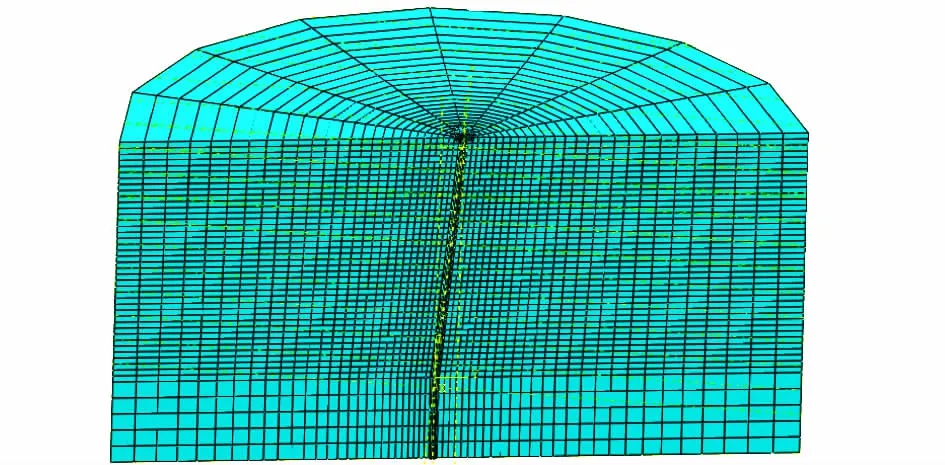
图2 有限元模型Fig.2 Finite element model

2.2 材料参数

土体采用Drucker-Prager弹塑性模型，桩体和承台均采用弹性模型。由于钢筋在各级荷载下未达到屈服应力，所以钢筋也采用弹性模型。具体材料参数见表1。

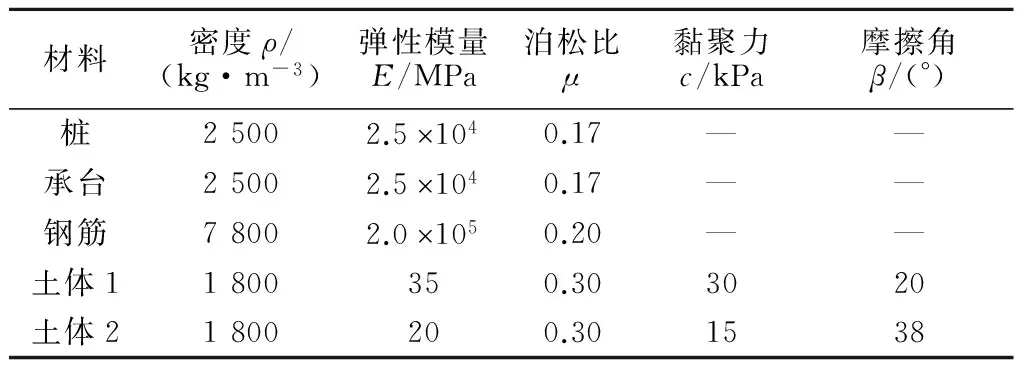
表1 材料参数

2.3 接触面

桩侧和土体的接触通过接触对来模拟，采用主-从接触算法，其中桩体表面定义为主面，土体表面定义为从面。接触对中面采用面对面的离散方法，以有限滑动方法反映桩-土接触面相对移动。不考虑接触面的黏聚力对水平受荷桩的贡献，因此桩-土接触面法向作用直接采用硬接触的方法模拟。桩侧和桩侧土的接触面间的摩擦采用库伦摩擦模型进行模拟，为使摩擦接触分析容易收敛，桩-土接触对采用了一个综合摩擦系数，通过对文献[13]现场试验结果模拟反演，得到综合摩擦系数为0.3较为合适。允许桩-土接触面有距离，以保证桩体与土体力的传递的合理性。

2.4 网格及边界条件

由于网格形状和疏密程度直接关系到数值计算的结果，本着保证计算精度和计算难度的原则，本文的三维模型将网格划分为靠近桩体的区域和远离桩体的区域，靠近桩体的区域网格划分较密，远离桩体的区域网格划分较粗。桩、土体采用三维实体缩减单元C3D8r，钢筋采用桁架T3D3单元。限制模型中土体侧向边界在2个水平方向上的位移及土体底边界在竖向和2个水平方向上的位移。

2.5 模型参数验证

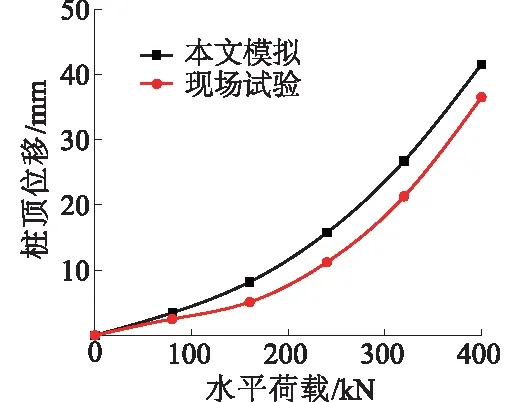
图3 水平荷载-位移曲线结果对比Fig.3 Comparison of lateral load-displacement curves

文献[13]叙述了杨建平等人在内蒙古进行的某灌注桩水平静载试验，该桩桩长为25 m，桩径为800 mm，混凝土为C40，场地土层以粉土为主，采用本文桩土材料参数模拟该试桩。图3为各级水平荷载作用下桩顶位移，从图3中可知，开始加载阶段数值模拟和现场试验的桩顶位移差别较小，当荷载较大时差别较明显，这主要是由于数值模型与现场实际场地的桩土弹性模量存在差距，而从整体来看数值模拟与现场试验得到的荷载-位移曲线趋势基本一致，说明模型参数是合理有效的。因此，依据此桩土参数进行水平荷载作用下斜桩承载变形研究是可行的。

3 数值模拟结果及分析

3.1 桩身倾角、长径比对单斜桩桩顶水平位移的影响

图4分别给出了长径比L/D为30，40，60时桩顶水平位移随水平荷载变化的曲线(Q-H曲线)。可以看出，整个加载过程中，正斜桩的Q-H曲线变化较平缓。同一水平荷载下正斜桩的桩顶水平位移均小于直桩和负斜桩，这与已有的研究成果正斜桩的水平承载力大于直桩和负斜桩是相符的。同一水平荷载作用下随着桩身倾角的增加，正斜桩桩顶水平位移不断减小且减小幅度明显，而负斜桩桩顶水平位移却出现增大的趋势。倾角为5°正负斜桩桩顶位移与直桩相差不大。如当L/D=30、水平荷载为210 kN时， 5°，10°，15°正斜桩桩顶水平位移分别为22.74，20.81，19.83 mm，相对直桩桩顶水平位移23.14 mm分别减小了1.73%，10.07%，14.30%；5°，10°，15°负斜桩桩顶水平位移分别为24.92，25.57，25.97 mm,相对直桩桩顶水平位移23.14 mm分别增加了7.69%，10.50%，12.23%。从整体来看，桩身倾角对于水平受荷斜桩桩顶水平位移的影响随着水平荷载增加而增大。在初始加载阶段水平荷载较小时倾角对斜桩的桩顶水平位移几乎没有影响。如图4在不同长径比下当水平荷载>60 kN时各桩身倾角斜桩与直桩的Q-H曲线基本重合。

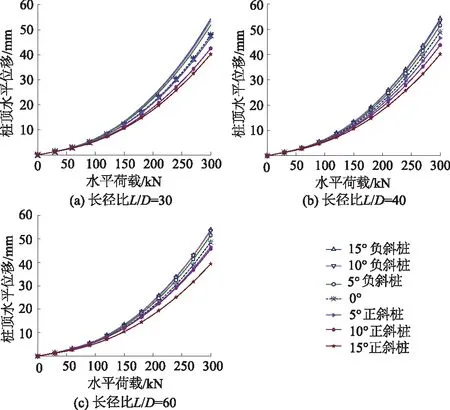
图4 斜桩水平荷载-位移曲线Fig.4 Lateral load-displacement curves of batter piles

通过对比分析图4中的(a)，(b)，(c)可以得到，长径比对斜桩桩顶水平位移影响较小。如当水平荷载为210 kN时， 15°正斜桩在长径比L/D=30，40，60时桩顶位移分别为19.83，19.84，19.42 mm，相互之间相差均在1%内；5°负斜桩在长径比L/D=30，40，60时桩顶位移分别为24.92，24.77，24.71 mm，相互之间相差也均在1%内。因此，在工程中以桩顶水平位移为控制指标的水平受荷斜桩，在一定桩土相对刚度下嵌固深度达到一定时，通过提高长径比来减小桩顶水平位移进而增加斜桩水平承载力是不合理的。

3.2 桩身倾角、长径比对单斜桩桩身弯矩的影响

图5给出了当水平荷载为300 kN、长径比分别为30，40，60时，不同桩身倾角斜桩的桩身弯矩曲线。从图5可以看出，在同一长径比下，相同水平荷载下正斜桩相同截面位置处的桩身弯矩要小于直桩和负斜桩的桩身弯矩；随着桩身倾角的增加，正斜桩桩身弯矩不断减小，而负斜桩呈现增大的趋势。当桩身倾角较小时，正负斜桩的桩身弯矩与直桩的桩身弯矩均相差不多。如在长径比为30时， 倾角为5°正、负斜桩的桩身最大弯矩分别为248.12，267.42 kN·m，较直桩身最大弯矩259.86 kN·m分别仅差-4.52%，+2.91%。这说明当水平受荷斜桩桩身倾角较小时可以参照直桩的方法进行设计。

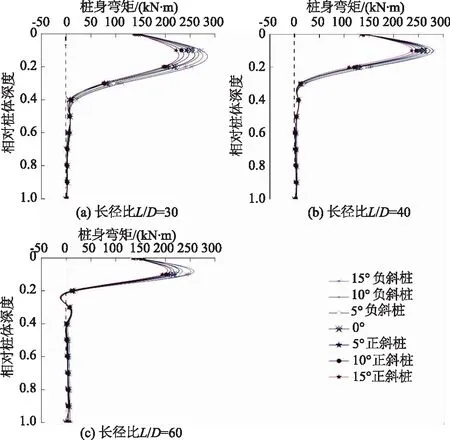
图5 不同长径比斜桩桩身弯矩Fig.5 Curves of bending moment along batter pile body in the presence of different slenderness ratios

从图5还可以看出，长径比为30时，桩身弯矩先逐渐增大再急剧衰减至0，最大桩身弯矩均出现在相对桩体深度0.13处；长径比为40和60时桩身弯矩发展到下部时开始出现反弯曲现象，最大桩身弯矩分别出现在相对桩体深度0.09和0.07处。所以，桩身倾角影响桩身弯矩的大小，并不影响桩身最大弯矩的所在位置深度。当桩身倾角相同时，对于长径比不同的水平受荷斜桩，桩身最大弯矩随长径比增加有减小的趋势。如倾角为15°负斜桩，长径比在30，40，60时桩身最大弯矩分别为285.11，280.05，258.19 kN·m； 倾角为5°正斜桩，长径比在30，40，60时桩身最大弯矩分别为248.12，254.01，217.86 kN·m。

3.3 竖向荷载对单斜桩桩顶水平位移的影响

图6为不同竖向荷载作用下，长径比为30时各倾角斜桩的桩顶水平位移随水平荷载变化的曲线。可以看出，在相同水平荷载作用下，负斜桩的桩顶水平位移随着桩身倾角增大而减小，这种规律随着竖向荷载越大越明显。如对于10°和20°负斜桩，在水平荷载为300 kN、竖向荷载为100 kN时，桩顶水平位移分别为47.67，42.95 mm，减小了9.9%；当水平荷载为300 kN、竖向荷载为150 kN时，桩顶的水平位移分别为45.00，38.04 mm，减小了15.5%。本次模拟在荷载施加时一次性施加竖向荷载而水平荷载逐渐施加，当水平荷载≤竖向荷载时，正斜桩的桩顶水平位移随着桩身倾角的增加而增大；当水平荷载>竖向荷载时，随着桩身倾角的增大而桩顶水平位移的增加量逐渐减小。例如倾角为5°和25°正斜桩，当水平荷载为60 kN、竖向荷载为100 kN时，正斜桩的桩顶水平位移分别为3.20，4.01 mm，增加了25.3%；而当水平荷载为210 kN、竖向荷载为100 kN时，桩顶位移分别为24.05，21.68 mm，减小了9.9%。

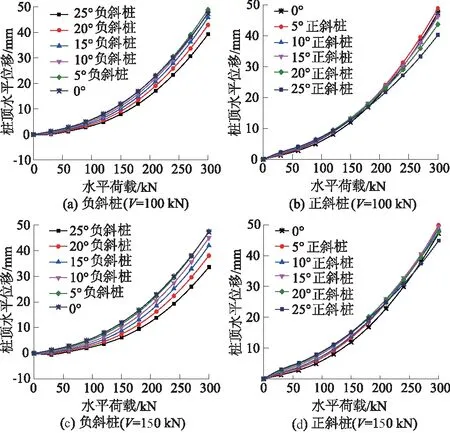
图6 不同竖向荷载下斜桩桩顶水平位移曲线Fig.6 Lateral displacement curves at head of batter pile under different vertical loads

从图6中还可以看出，在各斜桩桩顶水平位移曲线开始区段，较大桩身倾角的负斜桩桩顶产生了一定负水平位移，而正斜桩的桩顶水平位移曲线在第一区段的斜率明显较大。这是由于开始区段水平荷载较小，竖向荷载作用产生P-Δ效应，斜桩产生比直桩较大的水平位移，而竖向荷载引起的水平位移有利于减小负斜桩在水平荷载作用下产生的水平位移，却增大了正斜桩在水平荷载作用下的水平位移。

3.4 竖向荷载对斜桩桩身弯矩的影响

当水平荷载为300 kN时，长径比为30的斜桩在竖向荷载分别为100 kN和150 kN作用下的桩身弯矩如图7所示。可以看出，桩身弯矩从桩顶逐渐增加，达到最大值后又逐渐减小。由于竖向荷载作用，水平受荷斜桩桩身弯矩与无竖向荷载作用时的桩身弯矩存在很大区别。如在100 kN和150 kN竖向荷载作用下，倾角为25°负斜桩桩身最大弯矩分别为227.93，208.64 kN·m，均小于其他桩身倾角桩身最大弯矩；倾角为15°正斜桩桩身最大弯矩值最大，分别为268.24，280.13 kN·m。从各桩身弯矩曲线可以看出各斜桩的桩身最大弯矩均出现在相对桩身深度0.13处。在竖向荷载分别为0，100，150 kN的作用下，对于25°水平受荷正斜桩，桩身最大弯矩分别为211.12，241.39，258.19 kN·m；对于25°水平受荷负斜桩，桩身最大弯矩分别为272.49，227.93，208.64 kN·m。

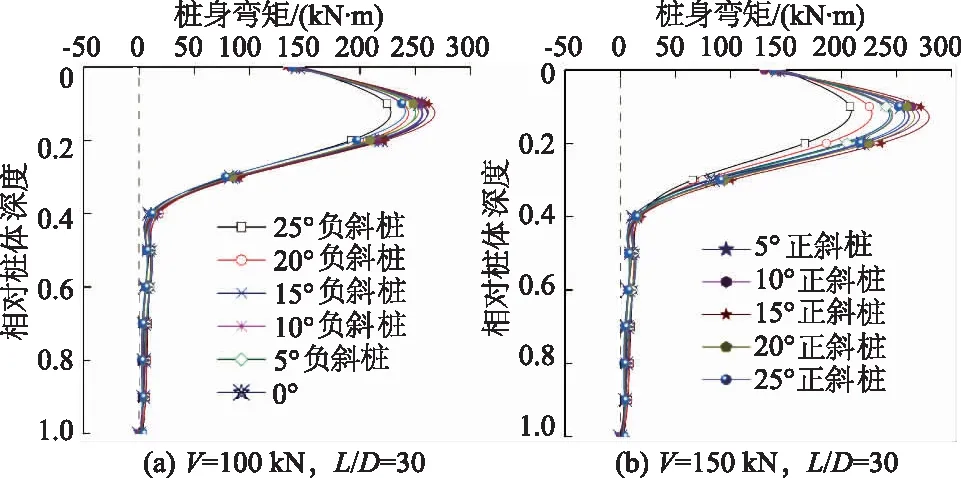
图7 不同荷载作用下斜桩桩身弯矩Fig.7 Curves of bending moment along batter pile body under different loads

由图7还可以看出相同桩身倾角斜桩随着竖向荷载的增加，负斜桩的桩身最大弯矩值不断减小，而正斜桩桩身弯矩最大值却出现先增加后减小的趋势。由于竖向荷载的影响，桩身弯矩的分布与仅受水平荷载相比，发生了很大变化，不能仅分别考虑再按照小变形叠加原理进行叠加，因此对于实际工程中同时受水平和竖向荷载的斜桩，特别是桩身倾角>5°的斜桩应考虑竖向荷载对桩身水平承载性状的影响。

4 结 论

本文通过数值模拟研究了桩身倾角、长径比及竖向荷载对单斜桩桩顶水平位移曲线、桩身弯矩以及桩-土接触压力的影响，可以得到以下结论：

(1) 在相同水平荷载作用下的单斜桩，正斜桩要比负斜桩和直桩的桩顶水平位移小，且随着桩身倾角的增加，正斜桩的这种优势越大。倾角<5°的斜桩的水平承载和直桩差别不大。相同条件下长径比对减小桩顶水平位移作用并不大。

(2) 相同条件下，桩身倾角只影响斜桩桩身弯矩的大小，而桩身最大弯矩所在位置基本一致。同一倾角下，长径比增加有减小桩身最大弯矩的趋势。

(3) 在竖向和水平荷载共同作用下，当水平荷载≤竖向荷载时，正斜桩的桩顶位移随着桩身倾角的增加而增大；但当水平荷载>竖向荷载时，倾角越大斜桩桩顶水平位移增加量却逐渐减小。而整个水平加载过程中，负斜桩的桩顶水平位移随着倾角增大而减小，且随着竖向荷载越大越明显。

(4) 相同条件下，正负水平受荷斜桩桩身最大弯矩值随竖向荷载的增加表现出不同的规律。负斜桩的桩身最大弯矩值随着竖向力的增大而减小，正斜桩的桩身最大弯矩值随着竖向力的增加而增大。

[1] 张麒蛰，卓卫东，范立础. 斜桩基础工作性状的研究进展[J]. 水利与建筑工程学报,2013,11(4)：60-66.

[2] 王云岗，章 光，胡 琦. 斜桩基础受力特性研究[J].岩土力学,2011,32(7):2184-2190.

[3] 吕凡任, 邵红才, 金耀华. 对称双斜桩基础水平承载力模型试验研究[J]. 长江科学院院报, 2013, 30(2): 67-70.

[4] 马庆华，邵 勇，朱进军. 水平荷载下承台-倾斜桩工作性状的数值分析[J]. 长江科学院院报, 2015, 32(11): 62-65.

[5] MEYERHOF G G，SASTRY V V R N. Bearing Capacity of Rigid Piles under Eccentric and Inclined Loads[J]. Canadian Geotechnical Journal, 1985, 22(3): 267-276.

[6] ZHANG L M, MCVAY M C, LAI P W. Centrifuge Modeling of Laterally Loaded Single Battered Piles in Sands[J]. Canadian Geotechnical Journal,1999, 36(6):1074-1084.

[7] ZHANG L M, MCVAY M C, HAN S J. Effects of Dead Loads on the Lateral Response of Battered Pile Groups[J]. Canadian Geotechnical Journal, 2002, 39(3):561-575.

[8] 凌道盛, 任 涛, 王云岗. 砂土地基斜桩水平承载力特性p-y曲线法[J]. 岩土力学,2013,34(1):155-162.

[9] 赵春风, 刘丰铭, 邱志雄,等. 砂土中竖向和水平荷载共同作用下的单桩承载特性研究[J]. 岩土工程学报, 2015, 37(1):183-190.

[10]袁廉华, 陈仁朋, 孔令刚, 等. 轴向荷载对斜桩水平承载特性影响试验及理论研究[J]. 岩土力学, 2013, 34 (7): 1958-1964.

[11]KARTHIGEYAN S, RAMAKRISHNA V V G S T, RAJAGOPAL K. Influence of Vertical Load on the Lateral Response of Piles in Sand[J]. Computers and Geotechnics, 2006, 33(2): 121-131.

[12]郑 刚，王 丽. 竖向及水平荷载加载水平、顺序对基桩载力的影响[J]. 岩土工程学报,2008,30(12):1796-1804.

[13]杨建平, 朴春德, 常鸿飞, 等. 水平荷载下灌注桩变形分布式检测及承载机制研究[J]. 岩石力学与工程学报, 2014,33(增1):2983-2988.

(编辑：陈 敏)

Numerical Analysis of Lateral Bearing Deformation Behaviorof Single Batter Pile with Cap

FAN Wen-fu1,2，CAO Wei-ping1

(1.College of Civil Engineering，Xi’an University of Architecture and Technology，Xi’an 710055，China； 2. TBEA SUNOASIS Co. Ltd., Urumqi 830011, China)

The influence of inclination angle and slenderness ratio, and especially vertical load, on the lateral response of single batter pile with cap was studied through 3-D finite element analysis. Results show that 1) under horizontal load, the lateral deformation of negative batter pile is larger than that of plumb pile, followed by positive batter pile. The difference of lateral deformation between batter pile and plumb pile increases with the increase of the inclination angle. The effect of slenderness ratio on the lateral deformation of batter pile is insignificant under the same condition; 2) the angle of batter pile affects only the value of moment along pile body under horizontal load. The position of the maximum moment of the pile is constant; 3) vertical load is favorable to decrease the lateral deformation of negative batter pile and increase the lateral deformation of positive batter pile; 4) the maximum moment of negative batter pile decreases as the increasing of vertical load, but it is in contrary with the positive batter pile.

batter pile; horizontal bearing performance; numerical analysis; slenderness ratio; inclined angle; vertical load

2015-08-25；

2015-09-28

樊文甫(1991-),男，河南西平人，硕士，主要从事桩基工程研究，(电话)0991-3851270(电子信箱)fanwfdyx@163.com。

10.11988/ckyyb.20150711

2016,33(10):121-125

TU473.11

A

1001-5485(2016)10-0121-05