含光伏发电系统配电网降损研究
江苏科技大学电气与信息工程学院 ■ 杨志豪 郑艳芳
含光伏发电系统配电网降损研究
江苏科技大学电气与信息工程学院 ■ 杨志豪 郑艳芳*
综述近10年来传统配电网降损方法及含有分布式电源的配电网优化配置研究成果,通过建模分析配电网中光伏电源容量、位置、运行方式对配电网网损的影响;最后结合光伏发电实际特点,提出将支持向量机和禁忌算法相结合的混合算法应用到配电网降损中的思想。
光伏发电;分布式电源;配电网;降损
0 引言
人类生存与发展离不开能源,随着煤、石油、天然气等不可再生能源的大量开采与消耗,化石燃料储量急剧下降,其燃烧导致的环境污染问题日益严重。为抓住能源引领的能源革命[1],我国“十三五”规划纲要提出:1)加快各级电网建设,重点加快特高压骨干网架和配电网建设;2)大规模开发清洁能源;3)严格控制中东部煤电;4)推动构建全球能源互联网。光伏发电(PV)是主要的分布式电源之一,它与配电网相连可为大电网提供备用,增强了电网的可靠性;同时由于PV启停方便等优点,可在电网中起到良好的调峰作用。其中,含PV的配电网建设及其对配电网损耗的影响和降损方法研究是实现“十三五”规划的一项重要工作。
近年来,国内外在配电网降损方法的研究上取得丰硕的研究成果。本文综述了近10年来传统配电网降损方法研究新成果,寻求对未来配电网建设具有指导意义的降损方法,以实现节能环保的目标。此外,PV在配电系统中的应用研究是未来实现清洁能源有效利用、降低中东部煤电份额的核心研究方向之一;结合PV的实际特点,通过建立网损模型,说明引入PV并合理配置PV对配电网网损的影响。
1 传统配电网降损方法研究
电网降损方法研究包含损耗分析研究和降损措施研究,其中,损耗分析研究是制定出有效降损措施的前提和根本保证。配电网的损耗分析是以电网参数为基础,通过计算理论损耗与统计损耗并进行比较,对配电网损耗中的技术损耗和管理损耗进行分析研究[2]。
在配电网技术降损方法上,张恺凯等[3]从线路电阻、配电变压器、电网功率因数低、线路日负荷不均衡、三相负荷不平衡、设备老化、接触不良、谐波等方面阐述技术损耗的降损措施,但并未考虑规划中的其他费用。杨文锋等[4]在城市中低压配电网降损方面分析常用配电网降损方法,并考虑了规划方案中的费用和运行约束的条件,构建出配电降损规划的优化决策模型,实现了最优的综合效益。郭秀钦等[5]根据配电网供电半径的长短、供电负荷的轻重及负荷的功率因数
等情况配置无功补偿装置,从而对中低压配电网络进行无功优化改造,使投资、运行和降损效果达到最佳,但未考虑到无功优化可能会增加变压器自身的损耗问题。史昌明等[6]将变压器损耗引入配电网无功优化模型,并考虑了不同负荷水平的影响,认为在无功优化方案中考虑变压器损耗适用于各种负荷水平。姚遥等[7]从提高供电可靠性和平滑负荷的角度出发,利用储能电池“既可在放电时作为储能节点,又可在充电时作为负荷节点”的特点,提出将储能技术引入配电网的思想,使负荷高峰和负荷低谷时的综合线损率降低。
在管理损耗方面,陈洪波[8]从管理损耗的角度分析了计量装置管理的问题,并从计量装置的选择、安装和防窃电措施角度提出了配电网的降损措施。
近年来,研究人员对PV并网的研究逐步深入,随着PV引入配电网,其对配电网网损的影响也十分显著。研究表明,在传统配电网中引入PV也可有效减少网损,进而结合目前流行的细菌菌落算法、禁忌搜索算法、自适应变异的粒子群优化算法等智能算法,可带来可观的经济效益。
2 引入PV对配电网网损的影响
2.1 引入PV后网损变化模型
简单潮流计算中,负载是由电网电源单方面供电,而接入PV后,负载通过电网电源和PV共同供电。本文采用文献[9,10]中的模型,并在此基础上通过求导分析,推导出PV引入配电网对网损的具体影响因素。假设两种情况下负荷大小均相同,不考虑线路首端到线路末端的压降,设全线路电压为U0,也不考虑负荷的三相不平衡。建立的理想模型见图1和图2。其中,Ps、Qs分别表示电网电源的有功功率、无功功率;PL、QL分别表示负荷的有功功率、无功功率;PG、QG分别表示光伏电源有功、无功功率;L表示电网电源与负荷之间的距离;LG表示电网电源与光伏电源之间的距离。

图1 未接入PV的模型
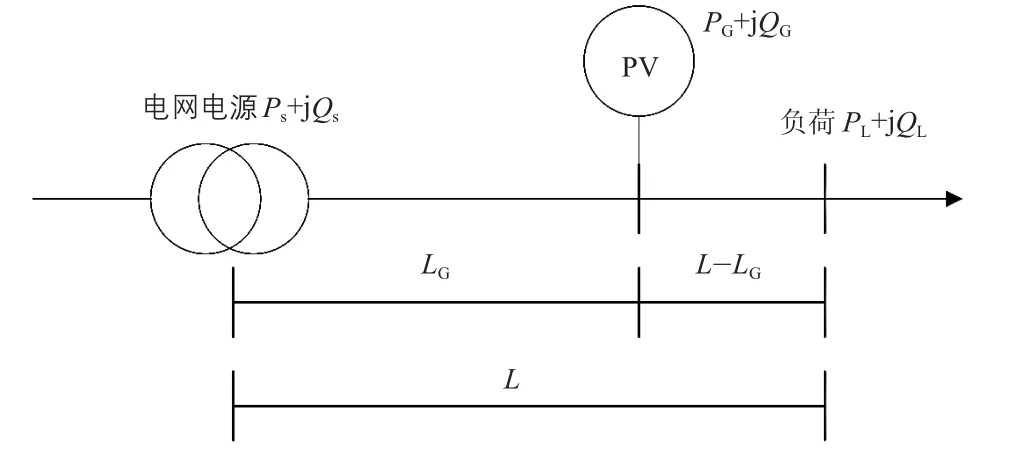
图2 接入PV的模型
引入PV可有效减少电网损耗,这是由于PV改变了系统的潮流分布。以往的电力系统中,电网电流在线路中大量流动,造成线路损耗增加;而加入PV后,一部分电源仍由电网电源供给,另一部分则由靠近负荷侧的PV供给。
1)系统流入负荷侧的单相电流为:

假设线路单相电阻率为r0(Ω/km),则未接入PV电源时,Is=IL,系统线路损耗为:

2)对于接入PV的电网来说,由于PV输出的单相电流IG:
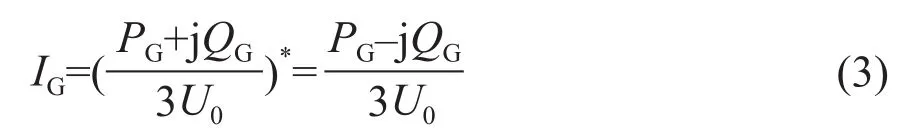
所以,电网电源流入的电流Is:

系统线路损耗分成电网到PV的损耗和PV到负荷的损耗,则在此情况下系统线路损耗为:

3)可见,接入PV与未接入PV,其功率损耗不同,其差值为:

由式(6)可知,PV接入的位置(LG),PV电源有功功率(PG)、无功功率(QG)各自出力的大小,都将影响接入PV后配电网网损。
2.2 引入PV的配电网损耗影响因素分析
2.2.1 PV相对负荷的位置
由式(6)可知,当PV接入的容量及功率因数不变时,ΔS的大小仅与LG的大小线性相关。而LG是电网电源与PV之间的距离,当LG越大,也就是在辐射型配电网网络中,PV越接近负荷中心,则ΔS越大;即相比于未接入PV,接入PV会有效减少网络损耗。
2.2.2 PV相对负荷的容量
由式(6)可知,当考虑PV相对负荷容量对网损影响时,需控制PV的位置及功率因数为一定值,即设LG为常数;设PV相对于负荷的比值为K,即则式(6)可变为:

可见,当K=1时,ΔS最大,即此时引入PV能最大限度减少网损;当K=2时,ΔS=0,表明此时引入PV与未引入PV对网损的影响相同;当K>2时,引入PV不仅不会减少网损,甚至会比不接入PV的网损还要大。
以上分析表明,在考虑PV接入配电网时,并非容量越大越好,当PV容量与负荷的容量相当时,可使配电网损耗最小。
2.2.3 PV运行时功率因数
由式(6)可知,要研究PV运行方式对ΔS的影响,需要控制PV的位置和容量不变,即LG和SG为定值。设PG=SGcosφ,QG=SGsinφ (φ为PV系统功率因数角),则:

ΔS对φ求导,可得:
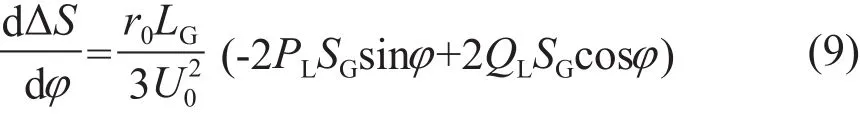
综上所述,在配电网中合理引入PV可显著减少网损,但与一般分布式电源不同,PV发出的直流电只能通过逆变器并网,需考虑负荷无功需求,合理配置无功补偿装置和容量,从而在不增加额外损耗的前提下,有效降低线损。
3 PV优化配置
在PV配置时,可结合智能算法进行优化。Vukobratovic 等[15]利用人工神经网络和遗传算法在DIgSILENT PowerFactory上对配电网功率损耗进行仿真,确定配电网中分布式电源的最优位置,但这种算法的参数设置较为复杂,运行速度慢。叶德意等[16]考虑了遗传算法及粒子群算法易早熟的特点,提出了自适应变异的粒子群优化算法,增强了粒子群优化算法跳出局部最优解的能力,具有良好的收敛精度和速度。Hussain等[17]利用微分进化的方法优化了在辐射式配电网中分布式电源的位置,具有处理不可微复杂优化问题的功能。陈海东[18]提出利用细菌菌落算法对分布式电源进行优化配置的方法,相比于萤火虫算
法收敛精度更高,也避免了粒子群算法计算时间长、运行复杂的缺点。
由于禁忌算法(TS)具有较强的局部搜索能力和“爬山”能力[19],支持向量机(SVM)[20]可有效解决有限样本、非线性及高维模式识别问题,TS和SVM结合可有效预测负荷,进而为PV的配置提供参考样本,最终降低配电网损耗,带来经济效益。
4 总结与展望
本文结合基本国情和基本国策,研究了近十年来在传统的配电降损方面取得的成果,并在此基础上,研究引入PV对整个配电网网损的影响。研究结果表明:1)含PV的配电网网损明显降低;2)含PV的配电网中,PV容量与负荷容量匹配时方可达到有效降损的目的;3)PV产生的无功功率可有效实现系统降损。此外,针对含PV的分布式电源系统分支繁多、结构复杂、节点不固定等特点,本文提出采用支持向量机和禁忌算法相结合的混合算法,该研究可直接指导引入PV的配电网建设及降损研究的仿真和实验。然而,对含分布式电源系统配电降损的研究工作任重而道远,尤其是线损计算和降损措施方面,需要积累更多的实验和实践数据,用来验证算法的精确性和方法的可行性,这也将是下一步研究的方向和目标。
研究表明,引入PV可有效降低配电网损耗,然而,也发现更多亟待解决的问题,如如何结合实际交直流混合电网的基本情况来选择PV容量、接入位置和功率因数等参数是有效实现配电网降损的一个关键技术问题。
下一步研究将集中在以下方面:1)结合实际交直流混合电网的基本情况,研究选择PV容量、接入位置和功率因数等参数的有效方法;2)研究含太阳能、风能、潮汐能等多种分布式发电系统的配电网降损方法;3)混合动力的车载、船载微电网的配电降损研究等。
[1] 张海龙. 中国新能源发展研究[D]. 吉林:吉林大学, 2014.
[2] 王彬宇. 城市中低压配电网损耗分析与降损技术选择方法[D]. 重庆: 重庆大学, 2014.
[3] 张恺凯, 杨秀媛, 卜从容, 等. 基于负荷实测的配电网理论线损分析及降损对策[J]. 中国电机工程学报, 2013, (S1): 92-97.
[4] 杨文锋, 王彬宇, 程卓, 等. 城市中低压配电网降损规划决策方法[J]. 电网技术, 2014, (9): 2598-2604.
[5] 郭秀钦, 郭大庆, 张永新, 等. 配电网节能降损优化改造方案的研究[J]. 电力电容器与无功补偿, 2014, (2): 43-49.
[6] 史昌明, 刁凤新, 杨朋威, 等. 考虑变压器损耗的配电网无功优化研究[J]. 水电能源科学, 2015, (12): 185-188.
[7] 姚遥, 刘东, 廖怀庆, 等. 含储能电池的配电网降损分析[J].华东电力, 2010, (5): 677-680.
[8] 陈洪波. 谈供电企业计量装置管理中存在的问题及对策[J].黑龙江科技信息, 2016, (2): 261.
[9] 马明. 分布式电源对配电网网损影响及配置的研究[D]. 南京: 南京理工大学, 2007.
[10] 涂有庆. 含分布式发电的配电网网损研究[D]. 湖南: 湖南大学, 2008.
[11] 司传涛, 肖静, 张阁, 等. 光伏发电系统无功支撑能力评估分析[J]. 广西电力, 2015, (6): 28-34.
[12] Braun M, Stetz T, Reimann T, et al. Optimal reactive powersupply in distribution networks——Technological and economic assessment for PV systems[A]. European Photovoltaic Solar Energy Conference and Exhibition[C], Hamburg, Germany, 2009, 3872-3881.
[13] 晁阳. 并网光伏发电系统无功电压控制研究[D]. 重庆: 重庆大学, 2014.
[14] Kabiri R, Holmes D G, McGrath B P. The influence of PV inverter reactive power injection on grid voltage regulation[A]. 2014 IEEE 5th International Symposium, Power Electronics for Distributed Generation System(PEDG) [C],Galway, 2014, 1-8.
[15] Vukobratovic M, Hederic Z, Hadziselimovic M. Optimal distributed generation placement in distribution network[J]. Electrical, Electronics, Signals, Communicationand Optimization(EESCO), 2014, 1176-1183.
[16] 叶德意, 何正友, 臧天磊. 基于自适应变异粒子群算法的分布式电源选址与容量确定[J]. 电网技术, 2011, (6): 155-160.
[17] Israfil Hussain, Anjan Kumar Roy. Optimal size and location of distributed generations using differential evolution(DE)[J]. Computational Intelligence and Signal Processing(CISP), 2012, (2): 57-61.
[18] 陈海东. 基于细菌菌落优化算法分布式电源优化配置[J].电力系统保护与控制, 2015, (21): 106-111.
[19] 田颖. 基于禁忌差分粒子群算法的分布式电源的选址和定容[D]. 北京: 华北电力大学, 2012.
[20] 刘蔚, 韩祯祥. 基于支持向量机的配电网重构[J]. 电力系统自动化, 2005, (7): 48-52.
2016-05-11
郑艳芳(1986—),女,博士、讲师,主要从事电容式传感器、微电网电能评估方面的研究。zhengyf@ynao.ac.cn

