基于SPH-ALE方法的波浪水槽数值模拟
李雪临,路 宽,韩林生,王 静,王花梅,石建军,朱 锐
(国家海洋技术中心,天津 300112)
基于SPH-ALE方法的波浪水槽数值模拟
李雪临,路 宽,韩林生,王 静,王花梅,石建军,朱 锐
(国家海洋技术中心,天津 300112)
为了精确模拟波浪传播,基于光滑粒子流体动力学及任意拉格朗日欧拉(SPH-ALE)方法建立二维数值波浪水槽,在原SPH方法中引入近似黎曼求解器替代人工黏性项,采用排斥力边界条件防止流体粒子穿透固边界,海绵层内采用指数型衰减函数来消除水槽末端的波浪反射,并对规则波的传播进行数值模拟。结果表明:与采用人工黏性项的原SPH方法相比,SPH-ALE方法能够无衰减地模拟波浪传播,并可有效减小固边界附近的粒子压力振荡。
波浪传播;光滑粒子;流体动力学;任意拉格朗日欧拉方法;数值模拟;波浪水槽;排斥力边界条件;海绵层
光滑粒子流体动力学(SPH)方法因其无网格、自适应以及拉格朗日性质,不需要特殊处理即可实现对复杂自由表面的精确模拟,特别适用于处理含大变形自由表面的流体动力学问题。Monaghan[1]于1994年首次将SPH方法应用于自由表面流动的数值模拟。Doring等[2]采用SPH方法研究了楔体入水和波浪与方箱的相互作用问题,模拟得到的楔体入水过程中垂向加速度和角加速度的历时曲线与实验结果吻合较好;Padova等[3]对不同Ursell数对应的非线性波和JONSWAP谱对应的随机波在规则或不规则底坡上的传播和崩破、卷破、破碎进行了SPH数值模拟和物理模型试验研究,探讨了不同的人工黏性经验系数和粒子初始间距与光滑长度之比对计算精度和效率的影响;高睿等[4]建立了求解孤立波沿斜坡传播、变形和破碎的数值模型,分析了孤立波浅化过程中波面、波高的变化特征以及波浪的不同破碎形态;郑兴等[5]提出了二阶精度近似的SPH方法(K2_SPH),并对溃坝、涌浪和大幅液舱晃荡等强非线性自由表面问题进行了研究,验证了K2_SPH方法在计算精度上的提升。以上研究中动量方程的扩散项均采用Monaghan提出的人工黏性项,但在利用数值波浪水槽研究波浪传播及其与结构物的相互作用时,人工黏性在大多数情况下往往因耗散过度而造成波浪传播过程的能量衰减[6],限制了此类SPH方法的应用。
为了避免人工黏性耗散性的影响,任冰等[7]基于Parshikov等[8]提出的Godunov型粒子动力学(GPH)方法,在修正的SPH方法(CSPM)中引入近似黎曼解,对动量方程的压力梯度项进行修正,并合理设置结构物的冲击边界,利用所建立的二维数值波浪水槽模拟了规则波对浪溅区结构物的冲击过程,并利用物理模型试验结果进行了验证。由于不需要人工黏性来保持数值稳定,波浪传播过程中的能量衰减较小,同时可减少压力场的数值噪音。Vila[9]将任意拉格朗日-欧拉方法与SPH方法相结合,提出另一种混合的SPH-ALE方法,同样引入近似黎曼解替代人工黏性,该方法采用守恒变量描述控制方程,与采用原始变量的Parshikov方法相比具有更小的数值振荡。
本文基于Vila提出的SPH-ALE方法建立数值波浪水槽,采用排斥力边界条件防止流体粒子穿透固边界,采用海绵层消波技术消除水槽末端的波浪反射,利用所建立的二维数值波浪水槽对规则波的传播进行了数值模拟,并与采用人工黏性的原SPH方法的计算结果进行了对比。
1 数值模型
主要对比采用人工黏性项的SPH模型和采用守恒变量描述的SPH-ALE模型。两种模型采用相同的边界条件和时间积分算法,主要区别在于控制方程中的连续方程和动量方程。计算程序是在SPHysics[10]的基础上进行二次开发。
1.1 控制方程的离散
1.1.1 连续方程和动量方程
a. SPH方法
采用人工黏性项的SPH粒子近似方程为
(1)
式中:r为粒子位置;v为粒子速度;ρ为粒子密度;m为粒子质量;P为粒子压力;g为重力加速度;Wij为光滑核函数;i、j分别代表相互作用的两个粒子。人工黏性项Πij为
(2)

b. SPH-ALE方法
Vila考虑求解相互作用的两个粒子间的一维黎曼问题,SPH中引入近似黎曼解,推导得到采用守恒变量描述的SPH-ALE方程为
(3)

本文采用HLLC(Harten Lax van Leer constant)近似黎曼求解器求解两粒子接触不连续的一维黎曼问题,采用二阶迎风格式MUSCL(monotone upstream centered schemes for conservation laws)[11],利用斜率限制器β重构粒子间界面两侧的状态并计算界面处通量,避免了Godunov一阶迎风格式的耗散性,从而具有更高的计算精度。
SPH-ALE方法的主要优点是能够有效减小流体粒子的压力和速度振荡[12]。由于不需要采用人工黏性项保持数值稳定性,该方法可有效地减少数值耗散,能更精确地模拟波浪传播及压力场,从而精确预测作用于结构物上的波浪力。
1.1.2 状态方程
在弱可压缩流体SPH方法中,采用Tait状态方程计算粒子压力:
(4)
式中:γ为绝热指数;c0为参考密度ρ0下的声速。由于弱可压缩条件的限制,声速应为流体最大速度的10倍以上,以保证流体密度的变化在1%以内。
1.1.3 XSPH方法
Monaghan[13]提出的XSPH方法能够保持粒子有序,经修正后粒子的速度由式(5)表示:
(5)
式中参数ε可取0.5。XSPH方法使粒子i的速度更接近于其附近粒子的平均速度。
1.2 边界条件
1.2.1 排斥力边界条件
采用由Monaghan等[14]提出、Rogers等[15]修正的排斥力边界条件,能有效防止流体粒子穿透固壁,且易于处理复杂边界。边界粒子施加在流体粒子上、沿固边界法线方向的作用力为
f=nR(ψ)P(ξ)ε(z,u⊥)
(6)
式中:n为边界粒子处的法向量;ψ为流体粒子到固边界的垂直距离,ξ为流体粒子与边界粒子确定的向量在该边界粒子处切向的投影,边界粒子处的法向量和切向量由与其相邻的边界粒子坐标来确定;u⊥为流体粒子速度在固边界法向上的投影。
1.2.2 造波边界条件
在SPH方法中通过给定运动固边界粒子的位移和速度,模拟造波板生成目标波浪。本文采用推板式造波,生成线性规则波时造波板粒子的水平位移Xp和速度Up分别如式(7)和式(8)所示:
ωt
(7)

(8)
式中:S为推板冲程;ω为波浪圆频率。
1.2.3 海绵层消波
采用类似于网格法的海绵层消波技术,在数值水槽末端设置一定长度的海绵层(至少一个波长)吸收反射波,选择指数型衰减函数[16]对位于海绵层内的流体粒子速度进行衰减,衰减函数形式如式(9)所示:
f(x)=1-exp(-α(Ls-(x-x0)))
(9)
式中:Ls为海绵层长度;x0为海绵层起始位置坐标;α为衰减系数,针对具体问题通过数值试验合理确定。
1.3 时间积分算法
本文采用的Sympletic时间积分算法在无摩擦或无黏性情况下具备时间可逆性[17],非常适合应用于无网格粒子法。Sympletic算法在半个时间步后粒子密度和位置为
(10)
(11)

2 波浪传播的数值模拟
2.1 计算参数设置
数值计算域如图1所示。数值水槽的长度L=17 m,推板式造波机位于水槽左端,距离水槽左边界0.1 m,入射波为规则波,波高H=0.1 m,周期T=1.5 s,波长Lw=2.83 m。水槽右端设置长度Ls=3 m的海绵层以防止波浪反射,衰减系数取α=3.0。水槽内水深d=0.5 m,初始状态下流体粒子呈均匀等距分布,Δx=Δz=0.02 m,计算域内的粒子总数为22 104个,其中边界粒子1 004个,流体粒子21 100个。

图1 数值计算域示意图(单位:m)
分别采用SPH方法和SPH-ALE方法对水槽内的波浪传播进行数值模拟。SPH方法中人工黏性项的自由参数υ取0.1或0.5,υ<0.1时可能会造成数值计算不稳定。SPH-ALE方法的计算结果对斜率限制器β的取值比较敏感,取值较小时(β≈1.0)仍会导致波浪传播的衰减,取值较大时(β≈1.5)则会造成波幅随时间增长的非物理效应[19],这里取β=1.3。
为了得到瞬时波面和波面历时曲线,采用Gómez-Gesteira等[20]提出的自由表面确定方法,从自由表面之上某一位置开始,以0.01 h为空间步长垂直向下按照式(12)依次估算各点的密度值。当估算密度首次超过参考密度的1/2时,将此位置标记为自由表面所在位置。
(12)
2.2 数值结果分析
图2为SPH方法、SPH-ALE方法计算的距造波板4 m处的波面历时曲线与线性理论解的对比结果(图中η为波面高程)。从图2可以看出,两种方法模拟的波浪相位均与线性理论解吻合较好,但SPH方法因人工黏性的耗散计算波高值明显偏小,υ=0.1时波面稳定后的计算平均波高比目标波高偏低约30%;而SPH-ALE方法的计算波高与目标波高偏差很小,波面稳定后的计算平均波高与目标波高的偏差仅为2.4%。此外,SPH-ALE方法计算的波面为非标准的正弦曲线,波峰处较尖陡而波谷处较平坦,能够比较真实地反映出波浪的非线性。

图2 波面历时曲线的数值解与线性理论解对比
海绵层内距造波板16 m处两种方法计算的波面历时曲线如图3所示。由图3可以看到,两种数值方法均表现出很好的消波效果,在距离海绵层起始位置2 m处的波面高程差最大不超过0.003 m,小于入射波高的3%。
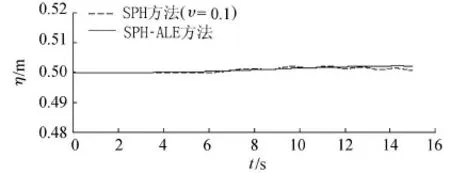
图3 海绵层内(x=16 m)波面历时曲线

图4 瞬时波面计算值与线性理论解对比
图4分别为t=10 s和t=15 s时,两种方法计算得到的瞬时波面与线性理论解的对比结果。其中,横坐标代表距造波板的水平距离。SPH方法人工黏性项的自由参数取υ=0.1和υ=0.5两种情况。由图4可看出,SPH方法计算的瞬时波面因人工黏性的耗散沿水槽长度方向逐渐衰减,且随人工黏性项自由参数υ的增大而衰减加剧,而自由参数υ取值过小又会造成数值计算的不稳定,因此使用SPH方法难以保证波浪传播数值模拟的精度。SPH-ALE方法计算的瞬时波面沿水槽长度方向几乎无任何衰减,与线性理论解的相位和波高值均吻合较好,同时波面形状也反映出了波浪的非线性,波面相对于线性理论解整体上略有抬升。
图5为t=15 s时SPH方法(υ=0.1)和SPH-ALE方法计算得到的流体压力场分布图。由图5可以看出,两种方法算得的自由表面都比较光滑,自由表面附近的压力分布均匀合理;但在造波板和水槽底部边界附近(图中黑色封口框范围),SPH方法的计算结果呈现出明显的粒子压力不连续现象,而SPH-ALE方法算得的压力场仍分布均匀,能够有效减小固边界附近的粒子压力振荡。

图5 计算流体压力场分布
3 结 论
基于SPH-ALE方法建立二维数值波浪水槽,分别采用SPH方法和SPH-ALE方法对规则波在数值水槽内的传播进行数值模拟,数值解和线性理论解的对比结果表明:因人工黏性的耗散作用,SPH方法计算的波面历时曲线和瞬时波面与线性理论解相比均有明显的衰减,而SPH-ALE方法的计算波面与线性理论解的相位和波高值均吻合很好,并可真实反映波浪的非线性;此外,在造波板和水槽底部边界附近,SPH方法计算的压力场呈现出明显的不连续现象,而SPH-ALE方法能够有效地减小固边界附近的粒子压力振荡。
[ 1 ] MONAGHAN J J.Simulating free surface flows with SPH[J].Journal of Computational Physics,1994,110(2):399-406.
[ 2 ] DORING M,OGER G,ALESSANDRINI B,et al.SPH simulations of floating bodies in waves[C]//Proceedings of ASME 2004 23rd International Conference on Offshore Mechanics and Arctic Engineering.New York: American Society of Mechanical Engineers,2004: 741-747.
[ 3 ] PADOVA D,DALRYMPLE R A,MOSSA M,et al.SPH simulations of regular and irregular waves and their comparison with experimental data[EB/OL].[2015-09-08].http://arxiv.org/ftp/arxiv/papers/0911/0911.1872.pdf.[ 4 ] 高睿,任冰,王国玉,等.孤立波浅化过程的SPH数值模拟[J].水动力学研究与进展(A辑),2010,25(5):620-629.(GAO Rui,REN Bing,WANG Guoyu,et al.SPH model of solitary waves shoaling on a mild sloping beach[J].Chinese Journal of Hydrodynamics,2010,25(5):620-629.(in Chinese))
[ 5 ] 郑兴,段文洋.K2_SPH方法及其对二维非线性水波的模拟[J].计算物理,2011,28(5):659-666.(ZHENG Xing,DUAN Wenyang.K2-SPH method and application for 2D nonlinear water wave simulation[J].Chinese Journal of Computational Physics,2011,28(5):659-666.(in Chinese))
[ 6 ] DALRYMPLE R A,ROGERS B D.Numerical modeling of water waves with the SPH method[J].Coastal Engineering,2006,53(2):141-147.
[ 7 ] 任冰,高睿,金钊,等.波浪对透空式结构物冲击作用的光滑粒子流体动力学数值模拟[J].海洋学报,2012,34(1):163-177.(REN Bing,GAO Rui,JIN Zhao,et al.The numerical simulation of wave slamming on an open-piled structure using the SPH model[J].Acta Oceanologica Sinica,2012,34(1): 163-177.(in Chinese))
[ 8 ] PARSHIKOV A N,MEDIN S A,LOUKASHENKO I I,et al.Improvements in SPH method by means of interparticle contact algorithm and analysis of perforation tests at moderate projectile velocities[J].International Journal of Impact Engineering,2000,24(8):779-796.
[ 9 ] VILA J P.On particle weighted methods and smooth particle hydrodynamics[J].Mathematical Models and Methods in Applied Sciences,1999,9(2):161-209.
[11] TORO E F.Shock-capturing methods for free-surface shallow flows[M].San Francisco: Wiley,2001.
[12] ROGERS B D,DALRYMPLE R A,STANSBY P K.Simulation of caisson breakwater movement using 2-D SPH[J].Journal of Hydraulic Research,2010,48(Sup1):135-141.
[13] MONAGHAN J J.On the problem of penetration in particle methods[J].Journal Computational Physics,1989,82(1):1-15.
[14] MONAGHAN J J,KOS A.Solitary waves on a Creatan Beach[J].Journal of Waterway,Port,Coastal and Ocean Engineering,1999,125(3):145-154.
[15] ROGERS B D,DALRYMPLE R A.SPH modeling of tsunami waves[J].Advances in Coastal and Ocean Engineering,2008,10:75-100.
[16] XU Rui.An improved incompressible smoothed particle hydrodynamics method and its application in free-Surface simulations[D].Manchester: University of Manchester,2009.
[17] LEIMKUHLER B J,REICH S,SKEEL R D.Integration methods for molecular dynamic IMA volume in mathematics and its application[M].Berlin: Springer,1997.
[18] MONAGHAN J J.Smoothed particle hydrodynamics[J].Reports on Progress in Physics,2005,68(8):1703-1759.
[19] ROGERS B D.Refined localized modelling of coastal flow features using adaptive quadtree grids[D].Oxford: Uiniversity of Oxford,2001.
Numerical simulation of wave flume based on SPH-ALE method
//LI Xuelin, LU kuan, HAN Linsheng, WANG Jing, WANG Huamei, SHI Jianjun, ZHU Rui
(NationalOceanTechnologyCenter,Tianjin300112,China)
In order to simulate wave propagation accurately, a two-dimensional numerical wave flume was constructed based on the smoothed particle hydrodynamics and arbitrary Lagrange Euler (SPH-ALE) method. An approximate Riemann solver was introduced to replace the artificial viscosity in the standard SPH model. The repulsive force boundary condition was used at the solid wall to prevent fluid particles from penetrating the solid boundary. The exponential damping function was used in the sponge layer to eliminate wave reflection at the end of the flume. The regular wave propagation was simulated in the constructed wave flume. The results show that, in comparison with the standard SPH method using artificial viscosity, the SPH-ALE method can simulate the wave propagation without attenuation and effectively reduce the pressure fluctuations near the solid boundaries.
wave propagation; smoothed particle; hydrodynamics; arbitrary Lagrange Euler method; numerical simulation; wave flume; repulsive force boundary condition; sponge layer
10.3880/j.issn.1006-7647.2016.06.008
国家自然科学基金 (51309056)
李雪临(1981—),男,工程师,博士,主要从事波浪与结构物相互作用研究。E-mail:xuedut@163.com
TV139.2
A
1006-7647(2016)06-0039-05
2015-09-08 编辑:郑孝宇)

