配制强度偏低可能是达不到设计强度等级的重要原因

戴镇潮（武警水电第二总队 退休高级工程师）

配制强度偏低可能是达不到设计强度等级的重要原因

戴镇潮（武警水电第二总队 退休高级工程师）

编者按：在工程实践中，由于种种原因，常会发生混凝土强度等级不足、达不到设计文件所要求的设计强度等级等情况，给建设工程带来极大的安全隐患。应对这种问题，目前还缺乏一套系统的解决方案。本期特别策划诚邀大家对造成混凝土强度等级不足的原因进行分析，并探讨相应的预防措施。

1 用什么方法确定达到的强度等级与否

评判是否达到设计要求的强度等级，首先要明确用什么来确定达到的强度等级。是用强度标准值，还是用强度平均值。

GB 50010—2002《混凝土结构设计规范》规定： “混凝土强度等级按立方体抗压强度标准值确定”。如现场抽取或试验室试验实测得试件强度平均值 fμ=37.0MPa，预估得强度标准差 σ=5.0MPa，则估计该批混凝土强度标准值fcu,k=37.0-1.645 5.0=28.8MPa，于是估计该批混凝土的强度等级为 C25。（强度标准值多用 fk代表，fcu,k代表立方体强度标准值）

但是，当前普遍存在的问题是直接用试件强度平均值fμ=37.0MPa 来确定强度等级，认为强度等级达到 C35。这是不正确的。因为试件强度平均值不是强度标准值，所确定的强度等级偏高。还有的甚至认为达到 C37，就更不正确了，规范中没有 C37 这个强度等级。

所以，应该以强度标准值 fcu,k确定强度等级；以强度平均值 fμ确定的强度等级是偏高的。若以强度平均值 fμ确定的强度等级仍未达到要求，则说明强度偏低太多。

由于试件强度是平均值 fμ，计算强度标准值 fcu,k需减去1.645σ。这就需要有强度标准差σ的数据。但强度标准差 σ几乎都是未知的，这也是直接用试件强度平均值来评判强度等级的一个原因。通常都只抽取少量试件进行检验，少量试件的强度标准差 s 的不定性很大，不能代表实际的强度标准差 σ，所以只能事先参考历史资料或有关规定预估得。

顺便指出的是，混凝土强度按正态分布计，标准差应和平均值同样重要。但实际是对标准差普遍不够重视，应加纠正。做到事先尽可能准确预估，事后尽可能多地积累实测资料，供以后预估用。

2 配制强度偏低可能是达不到设计强度等级的重要原因

配制强度是混凝土成分配合设计的基础。配制强度过高将增加水泥用量，提高成本，造成浪费；过低会达不到要求的强度等级。

配制强度 fcu,0是预期强度平均值，应稍大于设计强度平均值 fμ，才能使实际强度有较大的把握达到设计要求。fcu,0=fμ或 fcu,0＜fμ都是不正确的。fcu,0=fμ，在现场有利和不利于强度的因素出现的概率约各为 50%，则将只有约 50% 的强度＞fμ，达到设计要求，另约 50% 的强度＜fμ，达不到设计要求。fcu,0＜fμ，则将有 50% 以上的强度＜fμ，达不到设计要求。fcu,0都以 fμ为基准由式 (1) 或式 (2) 计算得：

式中：φ——强度加成系数，通常取 1.1～1.2。

式中：σ——预估强度标准差；

t——强度保证率系数，常用强度保证率为 80%～90%，相应的 t=0.84～1.28。

式 (1) 和式 (2) 都计算得：fcu,0＞fμ。

但 1996 年颁布的 JGJ/T 55—96《普通混凝土配合比设计规程》规定：fcu,0= fcu,k+1.645σ。是将设计强度标准值 fcu,k当作设计强度平均值 fμ，作为基准，偏低了1.645σ。由于fμ=fk+1.645σ，用 JGJ/T 55—96 计算得 fcu,0= fμ，显然是偏低的。

可能是已觉察到 JGJ/T 55—96 的 fcu,0偏低，2011 年修订颁布的 JGJ/T 55—2011《普通混凝土配合比设计规程》的式（4.0.1-1）改为：fcu,0≥ fcu,k+1.645σ。其中仍将设计强度标准值 fcu,k当作设计强度平均值 fμ；仅将等号“=”改为等于大于符号“≥”。以上已说明，采用等号“=”计算得的 fcu,0偏低；采用大于符号“＞”究竟应大多少没有说明，难以操作。

由上述，规定的配制强度偏低，很可能是强度达不到设计要求强度等级的重要原因。

为了有较大的把握达到设计要求强度等级，当前建议以fμ=（fcu,k+1.645σ）代入式 (1) 和式 (2) 将 JGJ/T 55—2011《普通混凝土配合比设计规程》的式 (4.0.1-1) 改为式 (3) 或式 (4)来计算 fcu,0：

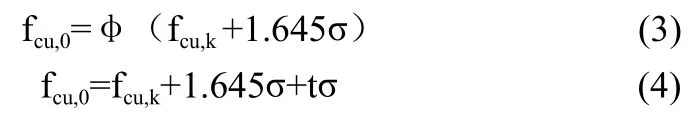
更加合理的 fcu,0建议按一次计量抽样检验方案确定，由式 (5) 计算得[1]：

n——抽样检验方案确定的抽取试件组数；

tα——与抽样检验的第Ⅰ类错误（或称错判概率、生产方损失）。α 相应的正态偏差，α 通常取 5%～10%，相应的，tα= -1.645～-1.28；

t1-β——与 1-β 相应的正态偏差。“1-”称为检验功效，也可称为合格判定的可靠性，β 是抽样检验的第Ⅱ类错误（或称漏判概率、使用方风险），通常取 5%～10%，相应的，t1-β=1.645～1.28。

3 关键是正确认识强度标准值

以上列举的，以强度平均值当作强度标准值来确定强度等级，所确定的强度等级偏高；又以强度标准值当作强度平均值来计算配制强度，所得配制强度偏低，是将强度标准值与强度平均值混淆造成的。原因是强度按正态分布计的观念尚未真正确立，没有认识到强度标准值是强度正态分布的代表，比强度平均值低 1.645σ。

早先，在混凝土强度按定值计时，设计计算用的强度只有一个定值。由于混凝土强度是十分接近正态分布的随机变量，这个定值实际上是强度平均值 fμ。在混凝土强度改按正态分布计后，强度不再只是一个定值，而是有很多很多个，需确定一个代表强度 fd来代表正态分布进行设计计算，所以fd也被称为设计计算强度。fd通常取小概率低强度（小概率分位值），fd= fμ+tσ，式中 t 为与 fd相应的正态偏差，当 fd＜fμ时，t 为负值。过去，曾采用概率为 0.135%、2%、2.3%、5% 等的分位值，相应的 t= -3、-2.05、-2、-1.645；现在统一为 5% 的分位值，称为强度标准值，以 fk代表，相应的t=-1.645，则 fk=fμ-1.645σ，见图1。GB/T 50107—2010 的3.02 条将强度标准值定义为：“混凝土抗压强度总体分布中的一个值，强度低于该值的概率应为 5%”。

图1　在强度正态分布N(fμ, σ2)中，标准值 fk与平均值fμ的关系

由于强度高低不同，强度标准值 fk有很多，为便于管理，将其划分为若干档次，称为强度等级，在等级值前加英文大写字母 C 表示，如 C10、C15……等。10≤fk＜15MPa 的为 C10；15≤fk＜20MPa 的为 C15；余类推。所以，强度标准值 fk和强度等级不完全等同。fk有很多，强度等级只有规范规定的几个。每个强度等级中有很多 fk，其中最小的 fk与该强度等级值相同，用来进行设计计算，称为设计强度标准值。

用设计强度标准值 fk代表强度正态分布进行设计计算，可简化当今采用的建筑结构设计方法（近似概率法）复杂的概率计算，使设计计算表达式的形式和原先采用的半概率半经验法一样简单，但是却掩盖了强度按正态分布计的实质，容易将设计强度标准值 fk误解为强度定值或强度平均值。所以应树立设计强度标准值 fk代表设计强度正态分布 N(fμ, σ2)的观念。

[1] 戴镇潮．混凝土配制强度和验收强度的确定方法[M]．北京：中国电力出版社，2008 年 8 月．