某雷达天线座齿轮传动副动力学研究

冯良祥，田振强

（中国电子科技集团公司第三十九研究所,西安 710065）

某雷达天线座齿轮传动副动力学研究

冯良祥，田振强

（中国电子科技集团公司第三十九研究所,西安 710065）

以某雷达天线为例，对其齿轮传动系统的技术与结构特点进行分析，在结合齿侧间隙对天线座齿轮伺服系统影响的基础上，建立了齿轮副间隙的非线性动力学模型，并对其进行数值求解，旨在为降低因齿侧间隙引起的系统振动和噪声，为提高雷达伺服系统的稳定性提供动力学基础。

雷达天线座；齿轮传动副；动力学特性

【DOI】10.13616/j.cnki.gcjsysj.2016.09.034

1 引言

因齿侧间隙的存在，雷达天线座齿轮在自身传动过程中会因内部齿轮相互作用产生接触—分离—接触的啮入啮出冲击，从而降低雷达伺服系统运行的稳定性，进而降低其定位精度。在此背景下，应进一步加强对雷达天线座齿轮传动系统技术、结构特点的研究，并在掌握齿侧间隙对伺服系统影响的基础上，加强对雷达天线座齿轮传动副动力学的研究，提高雷达的定位精度和工作的稳定性。

2 某雷达天线座齿轮传动系统特点

该雷达天线座传动系统由方位传动与俯仰传动系统组成，给出该雷达天线座齿轮传动系统的相关技术指标（见表1），由表1可知，某雷达天线的方位运动范围为：±180°，俯仰运动范围为：-91～+91°；加速度：方位/俯仰30°/s2；运动速度：方位/俯仰40°/s；传动回差：方位/俯仰≤0.05°。方位齿轮传动与俯仰齿轮传动的传动链均由行星齿轮减速器以及电机和末级齿轮副共同构成。

表1 某雷达天线的运动参数

在天线座齿轮传动机构进行反向运动的过程中，受齿侧间隙影响，主动齿轮必须要运行间隙大小的行程后方能够进一步带动从动齿轮进行反向运动，导致二者的运动产生延时，从而形成如图1所示的齿轮环状间隙，其中，x1和x2分别表示主动齿轮与从动齿轮的环形长度，即周长；b为主动齿轮转过的间隙大小的空程。由此，齿轮副传动的啮入与啮出过程便呈现出非单值的非线性关系[2]。

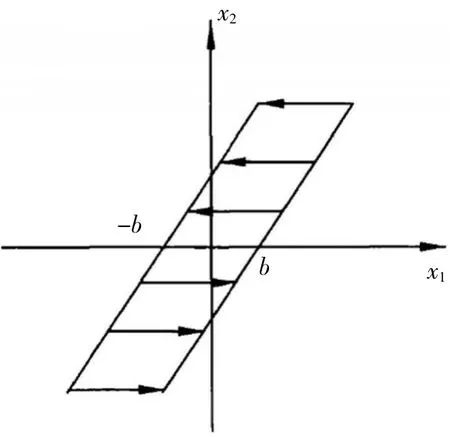
图1 环状间隙特性

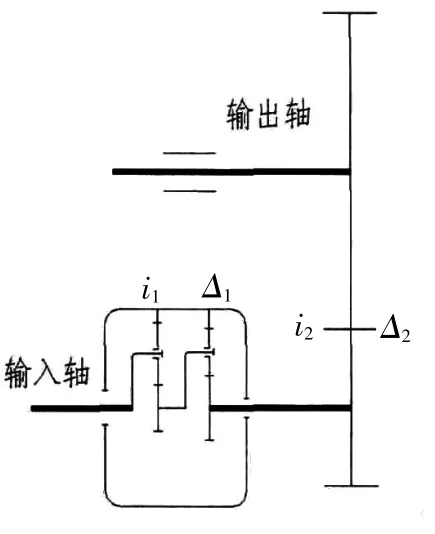
图2 雷达齿轮传动系统

图2给出了该雷达齿轮传动系统的示意图，图中，i1、Δ1为天线座传动系统输入轴减速机与末级齿轮副的传动比与间隙；i2和Δ2分别为天线座传动系统中输出轴减速机与末级齿轮副的传动比及间隙。由此，末级齿轮副传动的总间隙Δθ可表示为：

齿侧间隙对雷达伺服系统影响主要包括：（1）齿侧间隙本身的不确定性导致伺服系统的定位精度大幅下降，从而增加传动系统静态误差；（2）齿侧间隙导致主动与从动齿轮运动的不同步，使系统产生滞后效应，从而降低了伺服传动系统的稳定裕度，引发系统震荡，降低其稳定性[3]。

3 面向齿侧间隙的齿轮副动力学建模

3.1 非线性动力学模型构建

利用集中质量法来对其齿轮副传动的动力学模型予以构建，构建该雷达天线座齿轮副传动的动力学模型，如图3所示[1]。

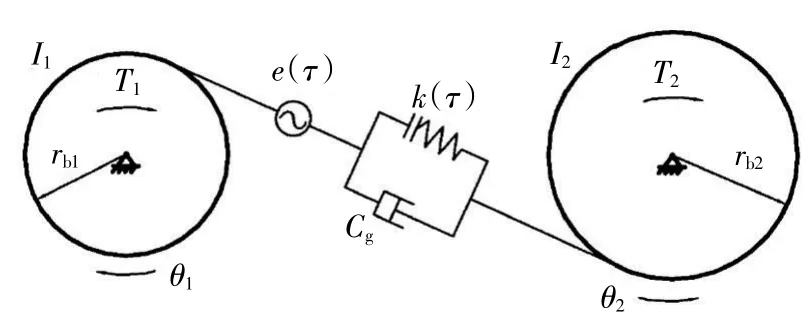
图3 某雷达齿轮系统动力学模型

rb1与rb2分别表示主动与从动齿轮的基圆半径；I1与I2分别为主动与从动齿轮的转动惯量；T1和T2分别为作用于主动与从动齿轮的扭矩；θ1和θ2则为两齿轮的扭转角位移；Cg和k（τ）则表示两齿轮啮合的阻尼系数与刚度。齿轮啮合的综合误差以e（τ）表示。

3.2 非线性运动微分方程的构建与分析

由牛顿第三定律可知，相互作用的2个物体之间的作用力和反作用力大小相等方向相反，而该雷达天线座齿轮传动副的转动惯量与扭矩则恰好满足牛顿第三定律中的阐述。基于此，建立齿轮传动系统的非线性运动微分方程，具体形式如式（2）所示：

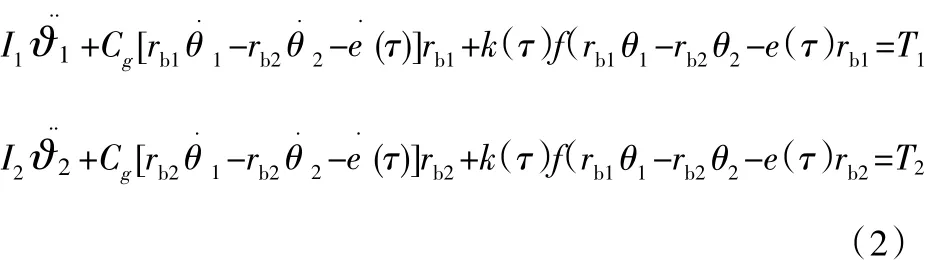
f（x）为齿轮传动系统中出现齿侧间隙时，齿轮啮合力所对应的非线性函数，假定某雷达天线座齿轮的齿侧间隙为2b，则f（x）具有显著的分段特征，对应的齿侧间隙的非线性函数可表示为式（3）所示形式，相应的函数形式如图4所示。

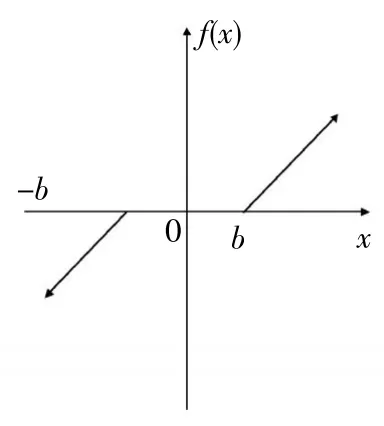
图4 齿侧间隙非线性函数

设该雷达天线座齿轮传动系统中的主动与从动齿轮在啮合线处发生的位移分别为x1与x2，则有，x1=rb1θ1；x2=rb2θ2，令式（3）第一式的两端同时除以rb1，第二式的两端同时除以rb2，进而得到齿轮传动系统的非线性运动微分方程的等效方程，并对其进行相应代换，进而得到：

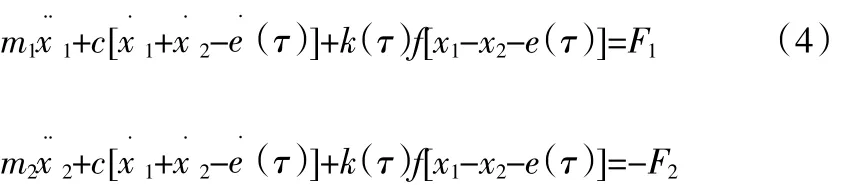
式中，m1为系统中齿轮的当量质量，表示为m1=I1/rb1；Fi为作用在齿轮i（i=1,2）的啮合力，表示为Fi=Ti/rbi,c为啮合阻尼，m2为齿轮的实际质量。为进一步获得齿轮间隙所发生变化的动态相应情况，对传动误差值进行分析可知，其通常以该齿轮在啮合线上所发生的直线位移进行度量。假定当该雷达天线座齿轮副中的从动齿轮的理论位置要比实际位置有所提前时，传动误差为正，当其实际位置比其理论位置提前时，相应的传动误差为负。设传动误差为δ，则其计算方法为：

由此，式（4）可进一步转换为齿侧间隙的动力学运动等效微分方程，即：

式中，m表示齿轮副的等效质量，其值为m=m1m2/m1+m2；F（τ）则表示为：

式中，Fu（τ）与Fv（τ）分别表示齿轮传动系统的外部激励与内部激励，通常情况下，内外部激励所对应的函数类型均为时间的周期函数，可以傅里叶级数的形式对二者进行表示，具体形式如下：

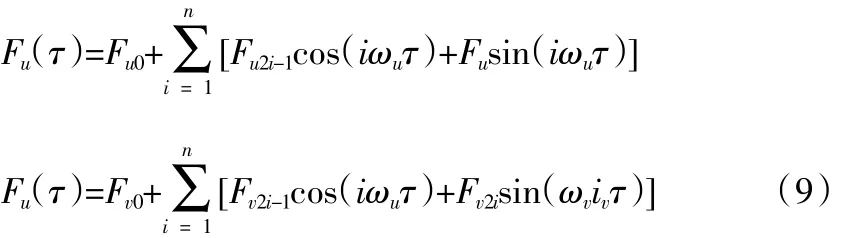
式中，Fu0与Fv0分别为齿轮传动系统中外部激励与内部激励的静态分量，n为傅里叶级数中的谐波数，ωu与ωv分别为齿轮副的内部激励频率与外部激励频率，Fu2i-1、Fv2i-1分别为外部激励及内部激励的交变分量中频率为（2i-1）倍激频的激励幅值；Fu2i、Fv2i分别为外部激励及内部激励的交变分量中频率为2i倍激频的激励幅值。该雷达天线座齿轮副传动系统中齿轮在啮合时，单齿与双齿啮合的运行是交替进行的，故在此过程中，齿轮啮合的刚度也会发生交替变化，加之对于不同的啮合位置而言，其所对应的啮合刚度也具有较大差异，这便导致了齿轮传动时，其啮合的刚度k（τ）受时间的影响较大，即呈现出显著的周期性，仍可利用傅里叶级数对齿轮啮合刚度k（τ）予以表示，具体形式为：

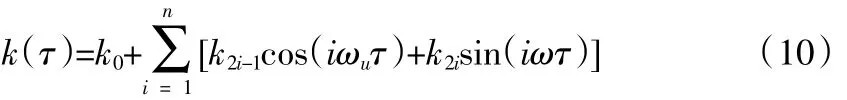
式中，k（τ）为齿轮的齿轮啮合刚度；k0为齿轮的平均啮合刚度，k2i-1、k2i为相应激励下交变分量中频率为（2i-1）倍和2i时齿轮的啮合刚度，ω为齿轮副的啮合频率，ω=2πzini/60，式中，ni和zi（i=1,2）分别为天线座齿轮副中相互啮合齿轮的转速以及齿轮数量，需要说明的是，对于同一个齿轮副而言，其啮合频率与内部激励频率相同，即ω=ωv。为进一步提高对非线性动力学运动方程求解的便利性，对其进行无量纲化处理，可得：

式中，ζ为阻尼比，ψ（t）为齿轮副的平均啮合刚度，f（x）仍然以式（6）所示为标准，在无量纲化方程中，P（t）包括的激励作用主要表现为2方面：（1）外扭矩载荷引起的振荡激励；（2）齿轮副中相互啮合的齿轮在啮合过程中产生的误差激励。对于整个天线座齿轮传动系统而言，基于静态传动误差的内部激励频率，即齿轮副中啮合齿轮的啮合频率，要远远超出外载荷扭矩本身的变化频率，故内部激励是导致该雷达天线座齿轮副传动产生噪声与振动的主要原因[4]。

3.3 非线性动力学模型的数值求解

3.3.1 系统初值的确定

为了进一步探究齿侧间隙的非线性对整个雷达天线座齿轮副传动系统动态特性的影响，做出以下假设：该雷达天线座齿轮副传动系统中，齿轮激励只有单频交变分量和平均分量构成，且对齿轮啮合刚度本身的时变性予以忽略，也就是将齿轮啮合刚度以齿轮副啮合刚度的均值予以取代，即ψ（t）=ψ（0）=1。假定齿轮本身的静态啮合力为Fm，相应的齿轮综合误差e为eacos（ωT+φe），由此，啮合刚度F（τ）则为：

分别令：φ0=φe+π；Pm=Fm/(b0k0)；Pa=ea/b0ω2；ω=ω/ωn，式中，k0为齿轮的平均啮合刚度；b0为假定的位移度量标准。由此，P（t）也可以齿轮啮合过程中的交变分量与平均分量相结合的形式予以表示，对其进行无量纲化处理可得：

式中，Pm和Pa分别表示齿轮副传动系统的平均激励和交变激励所对应的幅值，ω和φ0分别表示系统的激励频率与相对相位角，由此，可将某雷达天线座齿轮副传动系统的非线性运动微分方程的无量纲化形式即式（12）进一步简化为：

式（14）便是该雷达天线座齿轮传动副动力学系统最终的齿侧间隙非线性动力学微分方程，其初值分别为x（t0）和. x（t0）。

3.3.2 力学模型的数值求解

构建齿轮传动系统运行的微分方程：

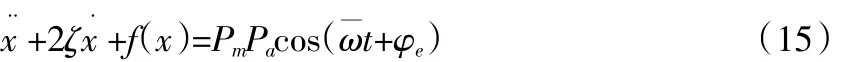
本文利用数值方法中的Runge-Kutta法对所购建的齿轮传动系统微分方程进行数值求解。给出已知条件微分方程：

式中，R为方程最大稳定域，对于给定的中止时刻，即tmax，引入足够大的数值N（N∈Z），对时间段[t0，tmax]进行离散，离散形式为：

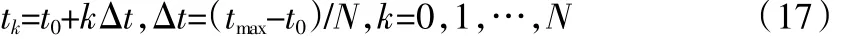
在较短的单位时间间隔内，对式（16）进行积分，由积分中值定理可得，势必会存在一个sk∈[tk，tk+1]使得：

由此，雷达天线座齿轮副的动力学求解问题的关键便转移到求出上式中的sk上来，将传动系统微分方程转化为如下形式：

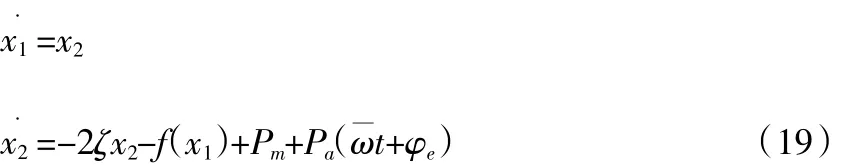
式中，x1则为齿轮传动系统间隙量纲化后的位移数值，x2表示齿轮量纲化后的速度，当雷达伺服系统运行过程中，相关操作人员给定x1与x2数值时，则能够根据式（19）准确确定出系统状态。

3.4 某雷达天线座齿轮副传动齿侧间隙的非线性模型的仿真分析

利用Matlab的Simulink仿真软件构建如图5所示的某雷达天线座齿轮副传动齿侧间隙的非线性动力学系统仿真模型，以阻尼比的变化为例对模型的响应情况进行分析。

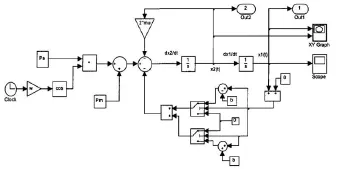
图5 齿轮间隙非线性动力学系统仿真模型

设定固定激励频率为ω，齿侧间隙为b，激励的幅值为Pm和Pa，令阻尼ζ比介于0～0.2的范围内变化，并观察其对所建立的系统响应特征的影响。取ω=1，Pm=0.1，Pa=0.2，b=1.0，当ζ= 0.1时，某雷达天线座齿轮传动副系统响应的时域波形图以及相平面图和功率谱分别如图6～图8所示。由图6～图8可知，系统在进行2周期运动时，所对应的响应波形不仅包括了同激振力相同的谐波，而且还包括了频率为ω/2的亚谐波回应。由相平面图可知，在天线座齿轮的啮合过程中，只存在齿面的啮合，且在此过程中会发生周期性的脱啮情况，但在齿背处却并不会相互啮合，说明系统从初始收敛状态开始到稳态的响应速度相对较快。

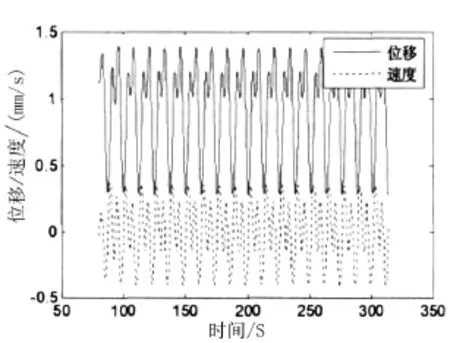
图6 ζ=0.1时时域波形图

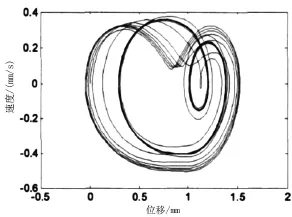
图7 ζ=0.1时相平面图

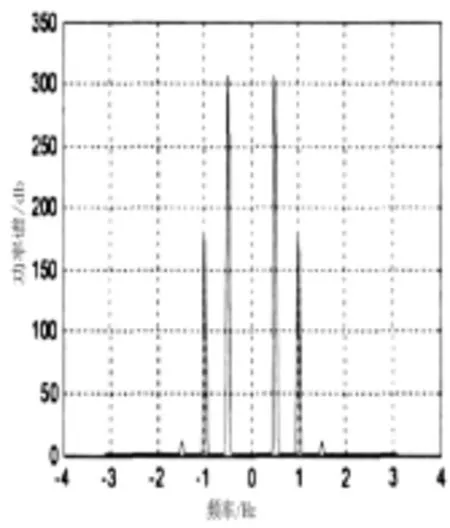
图8 ζ=0.1时功率谱

同理，阻尼比=0.2时的系统响应情况分别如图9～图11所示，由图9～图11可知，当阻尼比ζ由小变大的过程中，系统的运动周期则逐渐减小，当阻尼比大于某一值时，亚谐波振动消失。此外，当阻尼比较大时，齿轮啮合过程中只存在齿面冲击，而无齿背冲击，即齿背冲击随着阻尼比的增加而逐渐出现，当ζ=0.2时，齿背冲击最为严重。从系统的收敛至运动周期的时间层面分析，当ζ较大时，系统收敛值运动周期的时间最小，即系统收敛时间随着阻尼比的增加而减少[4]，由此可见，通过对阻尼比大小的合理调控能够较好地实现对某雷达齿轮系统碰撞行为的有效控制。

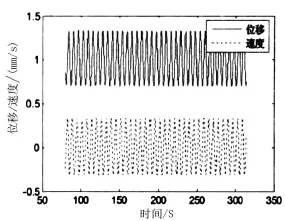
图9 ζ=0.2时时域波形图

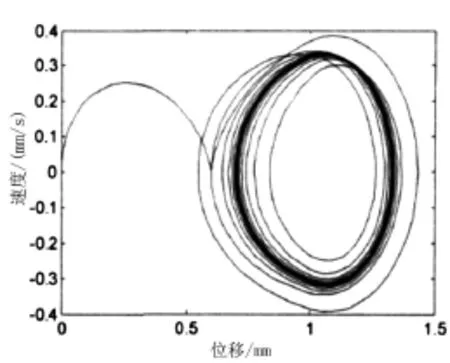
图10 ζ=0.2时时相平面图

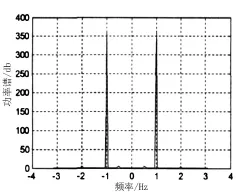
图11 ζ=0.2时功率谱

4 结论

通过对某雷达天线座齿轮传动系统的结构特点进行分析，进而对齿侧间隙对伺服系统的影响做出了系统探究，在此基础上，建立了面向齿侧间隙的齿轮副动力学模型，并利用Runge-Kutta数值方法对模型进行求解。研究结果表明，齿侧间隙对雷达天线座传动副系统的运行精度与运行的稳定性具有严重影响。将来还需进一步加强对雷达天线座传动副动力学系统的研究力度，为提高雷达伺服系统的定位精度和运行的稳定性提供可靠保障。

【1】顾吉丰，段勇军，平丽浩，等.雷达天线座传动系统转速波动影响因素分析[J].现代雷达，2013(2)：76-79.

【2】魏忠良，陈玉振，岳振兴.传动齿轮疲劳寿命的仿真分析[J].电子机械工程，2013(6)：56-58.

【3】胡长明，王长武，王贤宙.天线座多柔体动力学建模与仿真分析[J].电子机械工程，2015(5)：52-57.

【4】陈进，何成善，彭学文，等.模态参数改进为目标的前视天线座结构研究[J].噪声与振动控制，2013,6(13)∶39-42.

Study on the Gear Transmission Dynamics of a Radar Antenna Pedestal

FENG Liang-xiang,TIAN Zhen-qiang
(No.39 Institute of China Electronic Technology Group,Xi'an 710065,China)

Taking a radar antenna as an example,this paper analyzes the technology and structure characteristics of its gear transmission system.In combination with the influence of tooth side gap on gear servo system of the antenna pedestal,the nonlinear dynamic model of gear pair clearance is established,and the numerical solutionis made,in order to reduce vibration and noise from the backlash,and provide a kinetic basis for improving the stability of radar servo system.

radar antenna pedestal;gear transmission pair;dynamic characteristics

TH132.41

A

1007-9467（2016）09-0078-05

2016-08-05

冯良祥（1979～），男，河南新乡人，工程师，从事雷达传动系统结构设计研究。